深度学习应用篇-计算机视觉-图像分类[3]：ResNeXt、Res2Net、Swin Transformer、Vision Transformer等模型结构、实现、模型特点详细介绍

    <link rel="stylesheet" href="https://csdnimg.cn/release/blogv2/dist/mdeditor/css/editerView/kdoc_html_views-1a98987dfd.css">
    <link rel="stylesheet" href="https://csdnimg.cn/release/blogv2/dist/mdeditor/css/editerView/ck_htmledit_views-25cebea3f9.css">
            <div id="content_views" class="markdown_views prism-atom-one-dark">
                <svg xmlns="http://www.w3.org/2000/svg" style="display: none;">
                    <path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path>
                </svg>
                <p><img src="https://img-blog.csdnimg.cn/63a67cd7f8504a1d8411cc2f4a233385.png#pic_center" alt="在这里插入图片描述"><br> <strong>【深度学习入门到进阶】必看系列，含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等</strong></p>

在这里插入图片描述
专栏详细介绍：【深度学习入门到进阶】必看系列，含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等

本专栏主要方便入门同学快速掌握相关知识。后续会持续把深度学习涉及知识原理分析给大家，让大家在项目实操的同时也能知识储备，知其然、知其所以然、知何由以知其所以然。

声明：部分项目为网络经典项目方便大家快速学习，后续会不断增添实战环节（比赛、论文、现实应用等）

专栏订阅：

深度学习应用篇-计算机视觉-图像分类[3]：ResNeXt、Res2Net、Swin Transformer、Vision Transformer等模型结构、实现、模型特点详细介绍

1.ResNet

相较于VGG的19层和GoogLeNet的22层，ResNet可以提供18、34、50、101、152甚至更多层的网络，同时获得更好的精度。但是为什么要使用更深层次的网络呢？同时，如果只是网络层数的堆叠，那么为什么前人没有获得ResNet一样的成功呢？

1.1. 更深层次的网络？

从理论上来讲，加深深度学习网络可以提升性能。深度网络以端到端的多层方式集成了低/中/高层特征和分类器，且特征的层次可通过加深网络层次的方式来丰富。举一个例子，当深度学习网络只有一层时，要学习的特征会非常复杂，但如果有多层，就可以分层进行学习，如图1 所示，网络的第一层学习到了边缘和颜色，第二层学习到了纹理，第三层学习到了局部的形状，而第五层已逐渐学习到全局特征。网络的加深，理论上可以提供更好的表达能力，使每一层可以学习到更细化的特征。

1.2. 为什么深度网络不仅仅是层数的堆叠？

1.2.1 梯度消失 or 爆炸

但网络加深真的只有堆叠层数这么简单么？当然不是！首先，最显著的问题就是梯度消失/梯度爆炸。我们都知道神经网络的参数更新依靠梯度反向传播（Back Propagation），那么为什么会出现梯度的消失和爆炸呢？举一个例子解释。如图2 所示，假设每层只有一个神经元，且激活函数使用Sigmoid函数，则有：

       z 
      
      
      
        i 
       
      
        + 
       
      
        1 
       
      
     
    
      = 
     
     
     
       w 
      
     
       i 
      
     
     
     
       a 
      
     
       i 
      
     
    
      + 
     
     
     
       b 
      
     
       i 
      
     
     
     
     
       a 
      
      
      
        i 
       
      
        + 
       
      
        1 
       
      
     
    
      = 
     
    
      σ 
     
    
      ( 
     
     
     
       z 
      
      
      
        i 
       
      
        + 
       
      
        1 
       
      
     
    
      ) 
     
    
   
     z_{i+1} = w_ia_i+b_i\\ a_{i+1} = \sigma(z_{i+1}) 
    
   
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6389em; vertical-align: -0.2083em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">i</span><span class="mbin mtight">+</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2083em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.7333em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0269em;">w</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: -0.0269em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.8444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span><span class="mspace newline"></span><span class="base"><span class="strut" style="height: 0.6389em; vertical-align: -0.2083em;"></span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">i</span><span class="mbin mtight">+</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2083em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0359em;">σ</span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3117em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">i</span><span class="mbin mtight">+</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.2083em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span></span></p>

其中，

     σ 
    
   
     ( 
    
   
     ⋅ 
    
   
     ) 
    
   
  
    \sigma(\cdot) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0359em;">σ</span><span class="mopen">(</span><span class="mord">⋅</span><span class="mclose">)</span></span></span></span></span> 为sigmoid函数。</p>

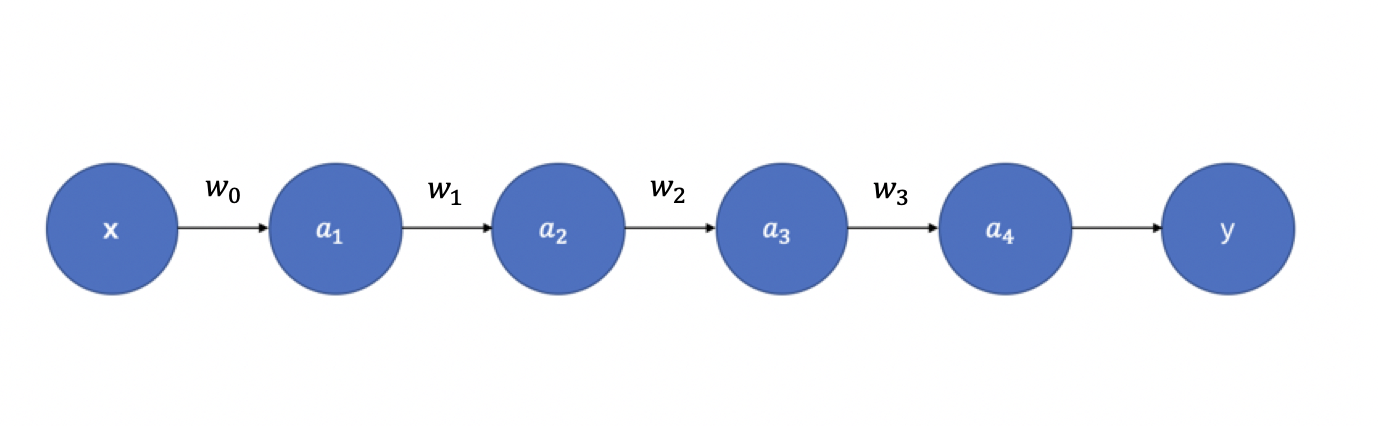
根据链式求导和反向传播，我们可以得到：

        ∂ 
       
      
        y 
       
      
      
      
        ∂ 
       
       
       
         a 
        
       
         1 
        
       
      
     
    
      = 
     
     
      
      
        ∂ 
       
      
        y 
       
      
      
      
        ∂ 
       
       
       
         a 
        
       
         4 
        
       
      
     
     
      
      
        ∂ 
       
       
       
         a 
        
       
         4 
        
       
      
      
      
        ∂ 
       
       
       
         z 
        
       
         4 
        
       
      
     
     
      
      
        ∂ 
       
       
       
         z 
        
       
         4 
        
       
      
      
      
        ∂ 
       
       
       
         a 
        
       
         3 
        
       
      
     
     
      
      
        ∂ 
       
       
       
         a 
        
       
         3 
        
       
      
      
      
        ∂ 
       
       
       
         z 
        
       
         3 
        
       
      
     
     
      
      
        ∂ 
       
       
       
         z 
        
       
         3 
        
       
      
      
      
        ∂ 
       
       
       
         a 
        
       
         2 
        
       
      
     
     
      
      
        ∂ 
       
       
       
         a 
        
       
         2 
        
       
      
      
      
        ∂ 
       
       
       
         z 
        
       
         2 
        
       
      
     
     
      
      
        ∂ 
       
       
       
         z 
        
       
         2 
        
       
      
      
      
        ∂ 
       
       
       
         a 
        
       
         1 
        
       
      
     
     
    
      = 
     
     
      
      
        ∂ 
       
      
        y 
       
      
      
      
        ∂ 
       
       
       
         a 
        
       
         4 
        
       
      
     
     
     
       σ 
      
      
       
      
        ′ 
       
      
     
    
      ( 
     
     
     
       z 
      
     
       4 
      
     
    
      ) 
     
     
     
       w 
      
     
       3 
      
     
     
     
       σ 
      
      
       
      
        ′ 
       
      
     
    
      ( 
     
     
     
       z 
      
     
       3 
      
     
    
      ) 
     
     
     
       w 
      
     
       2 
      
     
     
     
       σ 
      
      
       
      
        ′ 
       
      
     
    
      ( 
     
     
     
       z 
      
     
       2 
      
     
    
      ) 
     
     
     
       w 
      
     
       1 
      
     
    
   
     \frac{\partial y}{\partial a_1} = \frac{\partial y}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial a_1} \\ = \frac{\partial y}{\partial a_4}\sigma^{'}(z_4)w_3\sigma^{'}(z_3)w_2\sigma^{'}(z_2)w_1 
    
   
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 2.2074em; vertical-align: -0.836em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord mathnormal" style="margin-right: 0.0359em;">y</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 2.2074em; vertical-align: -0.836em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord mathnormal" style="margin-right: 0.0359em;">y</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span><span class="mspace newline"></span><span class="base"><span class="strut" style="height: 0.3669em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 2.2074em; vertical-align: -0.836em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3714em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord" style="margin-right: 0.0556em;">∂</span><span class="mord mathnormal" style="margin-right: 0.0359em;">y</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">σ</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.9925em;"><span class="" style="top: -2.9925em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.5795em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span class=""></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8278em;"><span class="" style="top: -2.931em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span class="mord mtight">′</span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0269em;">w</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.0269em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">σ</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.9925em;"><span class="" style="top: -2.9925em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.5795em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span class=""></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8278em;"><span class="" style="top: -2.931em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span class="mord mtight">′</span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0269em;">w</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.0269em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">σ</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.9925em;"><span class="" style="top: -2.9925em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.5795em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span class=""></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8278em;"><span class="" style="top: -2.931em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span class="mord mtight">′</span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.044em;">z</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.044em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0269em;">w</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.0269em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span><br> Sigmoid 函数的导数 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      σ 
     
     
      
     
       ′ 
      
     
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
  
    \sigma^{'}(x) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.1925em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">σ</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.9425em;"><span class="" style="top: -2.9425em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.5795em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span class=""></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8278em;"><span class="" style="top: -2.931em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span class="mord mtight">′</span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span></span></span></span></span> 如 <strong>图3</strong> 所示：</p>

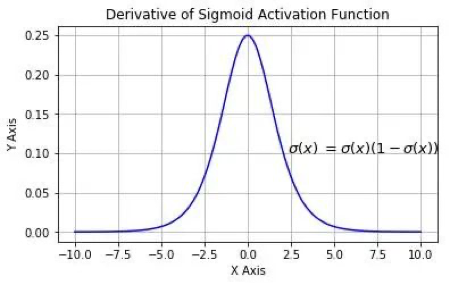
我们可以看到sigmoid的导数最大值为0.25，那么随着网络层数的增加，小于1的小数不断相乘导致

       ∂ 
      
     
       y 
      
     
     
     
       ∂ 
      
      
      
        a 
       
      
        1 
       
      
     
    
   
  
    \frac{\partial y}{\partial a_1} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.3773em; vertical-align: -0.4451em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.9322em;"><span class="" style="top: -2.655em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight" style="margin-right: 0.0556em;">∂</span><span class="mord mtight"><span class="mord mathnormal mtight">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3173em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.4461em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight" style="margin-right: 0.0556em;">∂</span><span class="mord mathnormal mtight" style="margin-right: 0.0359em;">y</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.4451em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span></span> 逐渐趋近于零，从而产生梯度消失。</p>

那么梯度爆炸又是怎么引起的呢？同样的道理，当权重初始化为一个较大值时，虽然和激活函数的导数相乘会减小这个值，但是随着神经网络的加深，梯度呈指数级增长，就会引发梯度爆炸。但是从AlexNet开始，神经网络中就使用ReLU函数替换了Sigmoid，同时BN（Batch Normalization)层的加入，也基本解决了梯度消失/爆炸问题。

1.2.2 网络退化

现在，梯度消失/爆炸的问题解决了是不是就可以通过堆叠层数来加深网络了呢？Still no！

我们来看看ResNet论文中提到的例子（见图4），很明显，56层的深层网络，在训练集和测试集上的表现都远不如20层的浅层网络，这种随着网络层数加深，accuracy逐渐饱和，然后出现急剧下降，具体表现为深层网络的训练效果反而不如浅层网络好的现象，被称为网络退化（degradation）。

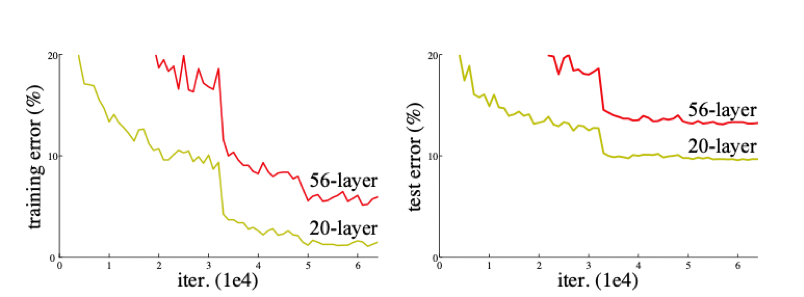
为什么会引起网络退化呢？按照理论上的想法，当浅层网络效果不错的时候，网络层数的增加即使不会引起精度上的提升也不该使模型效果变差。但事实上非线性的激活函数的存在，会造成很多不可逆的信息损失，网络加深到一定程度，过多的信息损失就会造成网络的退化。

而ResNet就是提出一种方法让网络拥有恒等映射能力，即随着网络层数的增加，深层网络至少不会差于浅层网络。

1…3. 残差块

现在我们明白了，为了加深网络结构，使每一次能够学到更细化的特征从而提高网络精度，需要实现的一点是恒等映射。那么残差网络如何能够做到这一点呢？

恒等映射即为

     H 
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
     = 
    
   
     x 
    
   
  
    H(x) = x 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0813em;">H</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">x</span></span></span></span></span>，已有的神经网络结构很难做到这一点，但是如果我们将网络设计成 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     H 
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
     = 
    
   
     F 
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
     + 
    
   
     x 
    
   
  
    H(x) = F(x) + x 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0813em;">H</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">F</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">x</span></span></span></span></span>，即 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     F 
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
     = 
    
   
     H 
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
     − 
    
   
     x 
    
   
  
    F(x) = H(x) - x 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">F</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0813em;">H</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">x</span></span></span></span></span>，那么只需要使残差函数 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     F 
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
     = 
    
   
     0 
    
   
  
    F(x) = 0 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">F</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.6444em;"></span><span class="mord">0</span></span></span></span></span>，就构成了恒等映射 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     H 
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
     = 
    
   
     F 
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
  
    H(x) = F(x) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0813em;">H</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">F</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span></span></span></span></span>。</p>

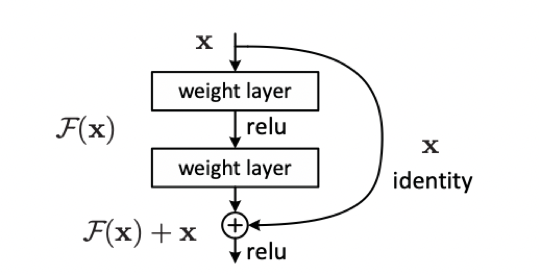
残差结构的目的是，随着网络的加深，使

     F 
    
   
     ( 
    
   
     x 
    
   
     ) 
    
   
  
    F(x) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">F</span><span class="mopen">(</span><span class="mord mathnormal">x</span><span class="mclose">)</span></span></span></span></span> 逼近于0，使得深度网络的精度在最优浅层网络的基础上不会下降。看到这里你或许会有疑问，既然如此为什么不直接选取最优的浅层网络呢？这是因为最优的浅层网络结构并不易找寻，而ResNet可以通过增加深度，找到最优的浅层网络并保证深层网络不会因为层数的叠加而发生网络退化。</p>

参考文献

[1] Visualizing and Understanding Convolutional Networks

[2] Deep Residual Learning for Image Recognition

2. ResNeXt（2017）

ResNeXt是由何凯明团队在2017年CVPR会议上提出来的新型图像分类网络。ResNeXt是ResNet的升级版，在ResNet的基础上，引入了cardinality的概念，类似于ResNet，ResNeXt也有ResNeXt-50，ResNeXt-101的版本。那么相较于ResNet，ResNeXt的创新点在哪里？既然是分类网络，那么在ImageNet数据集上的指标相较于ResNet有何变化？之后的ResNeXt_WSL又是什么东西？下面我和大家一起分享一下这些知识。

2.1 ResNeXt模型结构

在ResNeXt的论文中，作者提出了当时普遍存在的一个问题，如果要提高模型的准确率，往往采取加深网络或者加宽网络的方法。虽然这种方法是有效的，但是随之而来的，是网络设计的难度和计算开销的增加。为了一点精度的提升往往需要付出更大的代价。因此，需要一个更好的策略，在不额外增加计算代价的情况下，提升网络的精度。由此，何等人提出了cardinality的概念。

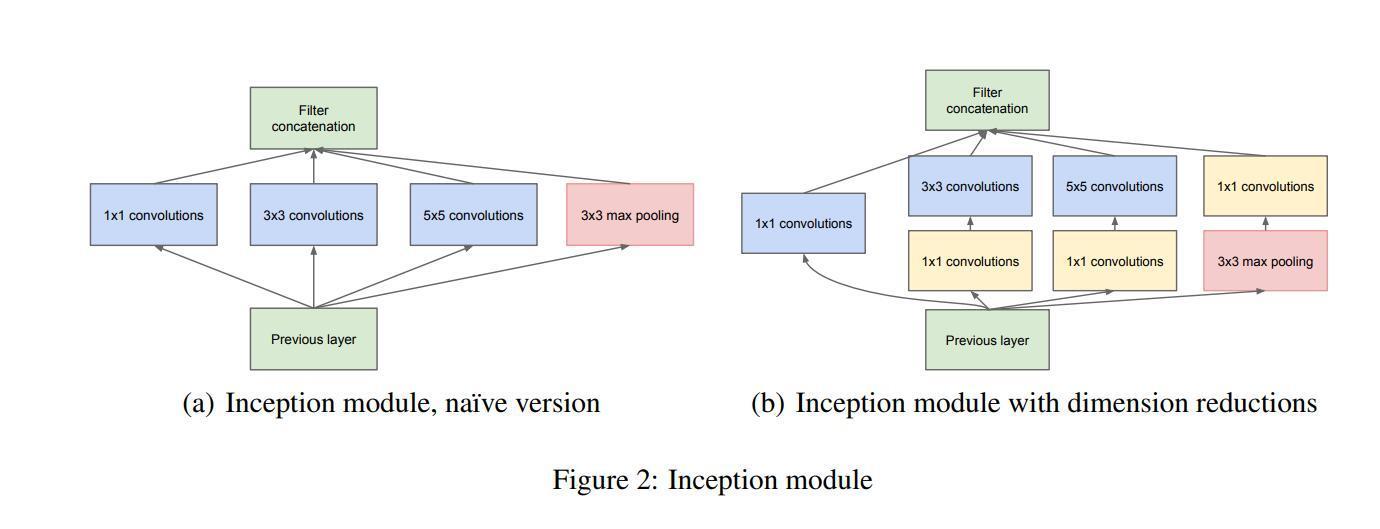
下图是ResNet（左）与ResNeXt（右）block的差异。在ResNet中，输入的具有256个通道的特征经过1×1卷积压缩4倍到64个通道，之后3×3的卷积核用于处理特征，经1×1卷积扩大通道数与原特征残差连接后输出。ResNeXt也是相同的处理策略，但在ResNeXt中，输入的具有256个通道的特征被分为32个组，每组被压缩64倍到4个通道后进行处理。32个组相加后与原特征残差连接后输出。这里cardinatity指的是一个block中所具有的相同分支的数目。

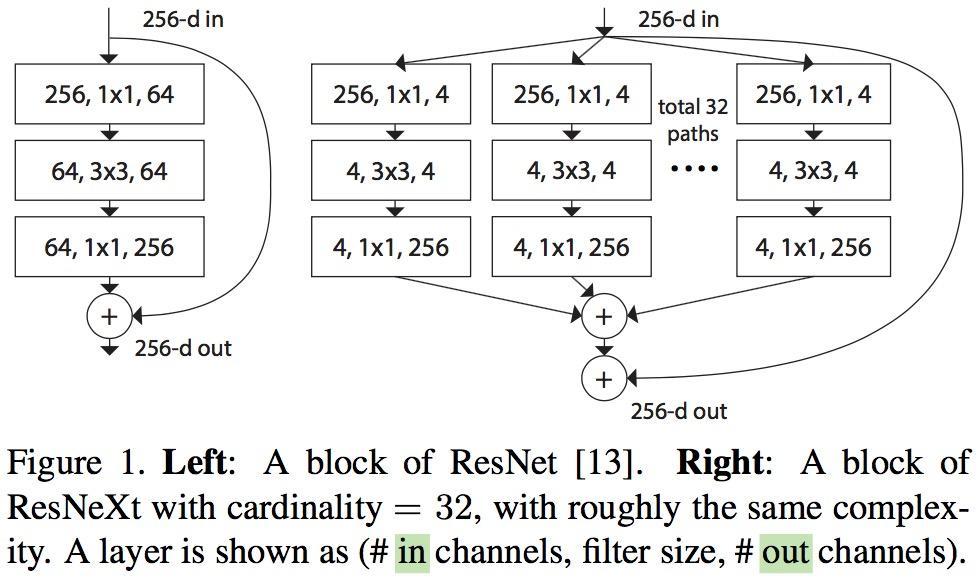
下图是InceptionNet的两种inception module结构，左边是inception module的naive版本，右边是使用了降维方法的inception module。相较于右边，左边很明显的缺点就是参数大，计算量巨大。使用不同大小的卷积核目的是为了提取不同尺度的特征信息，对于图像而言，多尺度的信息有助于网络更好地对图像信息进行选择，并且使得网络对于不同尺寸的图像输入有更好的适应能力，但多尺度带来的问题就是计算量的增加。因此在右边的模型中，InceptionNet很好地解决了这个问题，首先是1×1的卷积用于特征降维，减小特征的通道数后再采取多尺度的结构提取特征信息，在降低参数量的同时捕获到多尺度的特征信息。

ResNeXt正是借鉴了这种“分割-变换-聚合”的策略，但用相同的拓扑结构组建ResNeXt模块。每个结构都是相同的卷积核，保持了结构的简洁，使得模型在编程上更方便更容易，而InceptionNet则需要更为复杂的设计。

2.2 ResNeXt模型实现

ResNeXt与ResNet的模型结构一致，主要差别在于block的搭建，因此这里用paddle框架来实现block的代码

class ConvBNLayer(nn.Layer):
    def __init__(self, num_channels, num_filters, filter_size, stride=1,
                 groups=1, act=None, name=None, data_format="NCHW"
                ):
        super(ConvBNLayer, self).__init__()
        self._conv = Conv2D(
            in_channels=num_channels, out_channels=num_filters,
            kernel_size=filter_size, stride=stride,
            padding=(filter_size - 1) // 2, groups=groups,
            weight_attr=ParamAttr(name=name + "_weights"), bias_attr=False,
            data_format=data_format
        )
        if name == "conv1":
            bn_name = "bn_" + name
        else:
            bn_name = "bn" + name[3:]
        self._batch_norm = BatchNorm(
            num_filters, act=act, param_attr=ParamAttr(name=bn_name + '_scale'),
            bias_attr=ParamAttr(bn_name + '_offset'), moving_mean_name=bn_name + '_mean',
            moving_variance_name=bn_name + '_variance', data_layout=data_format
        )
<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> inputs<span class="token punctuation">)</span><span class="token punctuation">:</span>
    y <span class="token operator">=</span> self<span class="token punctuation">.</span>_conv<span class="token punctuation">(</span>inputs<span class="token punctuation">)</span>
    y <span class="token operator">=</span> self<span class="token punctuation">.</span>_batch_norm<span class="token punctuation">(</span>y<span class="token punctuation">)</span>
    <span class="token keyword">return</span> y

class BottleneckBlock(nn.Layer):
def init(self, num_channels, num_filters, stride, cardinality, shortcut=True,
name=None, data_format=“NCHW”
):
super(BottleneckBlock, self).init()
self.conv0 = ConvBNLayer(num_channels=num_channels, num_filters=num_filters,
filter_size=1, act=‘relu’, name=name + “_branch2a”,
data_format=data_format
)
self.conv1 = ConvBNLayer(
num_channels=num_filters, num_filters=num_filters,
filter_size=3, groups=cardinality,
stride=stride, act=‘relu’, name=name + “_branch2b”,
data_format=data_format
)

    self<span class="token punctuation">.</span>conv2 <span class="token operator">=</span> ConvBNLayer<span class="token punctuation">(</span>
        num_channels<span class="token operator">=</span>num_filters<span class="token punctuation">,</span>
        num_filters<span class="token operator">=</span>num_filters <span class="token operator">*</span> <span class="token number">2</span> <span class="token keyword">if</span> cardinality <span class="token operator">==</span> <span class="token number">32</span> <span class="token keyword">else</span> num_filters<span class="token punctuation">,</span>
        filter_size<span class="token operator">=</span><span class="token number">1</span><span class="token punctuation">,</span> act<span class="token operator">=</span><span class="token boolean">None</span><span class="token punctuation">,</span>
        name<span class="token operator">=</span>name <span class="token operator">+</span> <span class="token string">"_branch2c"</span><span class="token punctuation">,</span>
        data_format<span class="token operator">=</span>data_format
    <span class="token punctuation">)</span>

    <span class="token keyword">if</span> <span class="token keyword">not</span> shortcut<span class="token punctuation">:</span>
        self<span class="token punctuation">.</span>short <span class="token operator">=</span> ConvBNLayer<span class="token punctuation">(</span>
            num_channels<span class="token operator">=</span>num_channels<span class="token punctuation">,</span> num_filters<span class="token operator">=</span>num_filters <span class="token operator">*</span> <span class="token number">2</span>
            <span class="token keyword">if</span> cardinality <span class="token operator">==</span> <span class="token number">32</span> <span class="token keyword">else</span> num_filters<span class="token punctuation">,</span>
            filter_size<span class="token operator">=</span><span class="token number">1</span><span class="token punctuation">,</span> stride<span class="token operator">=</span>stride<span class="token punctuation">,</span>
            name<span class="token operator">=</span>name <span class="token operator">+</span> <span class="token string">"_branch1"</span><span class="token punctuation">,</span> data_format<span class="token operator">=</span>data_format
        <span class="token punctuation">)</span>

    self<span class="token punctuation">.</span>shortcut <span class="token operator">=</span> shortcut

<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> inputs<span class="token punctuation">)</span><span class="token punctuation">:</span>
    y <span class="token operator">=</span> self<span class="token punctuation">.</span>conv0<span class="token punctuation">(</span>inputs<span class="token punctuation">)</span>
    conv1 <span class="token operator">=</span> self<span class="token punctuation">.</span>conv1<span class="token punctuation">(</span>y<span class="token punctuation">)</span>
    conv2 <span class="token operator">=</span> self<span class="token punctuation">.</span>conv2<span class="token punctuation">(</span>conv1<span class="token punctuation">)</span>

    <span class="token keyword">if</span> self<span class="token punctuation">.</span>shortcut<span class="token punctuation">:</span>
        short <span class="token operator">=</span> inputs
    <span class="token keyword">else</span><span class="token punctuation">:</span>
        short <span class="token operator">=</span> self<span class="token punctuation">.</span>short<span class="token punctuation">(</span>inputs<span class="token punctuation">)</span>

    y <span class="token operator">=</span> paddle<span class="token punctuation">.</span>add<span class="token punctuation">(</span>x<span class="token operator">=</span>short<span class="token punctuation">,</span> y<span class="token operator">=</span>conv2<span class="token punctuation">)</span>
    y <span class="token operator">=</span> F<span class="token punctuation">.</span>relu<span class="token punctuation">(</span>y<span class="token punctuation">)</span>
    <span class="token keyword">return</span> y

2.3 ResNeXt模型特点

ResNeXt通过控制cardinality的数量，使得ResNeXt的参数量和GFLOPs与ResNet几乎相同。
通过cardinality的分支结构，为网络提供更多的非线性，从而获得更精确的分类效果。

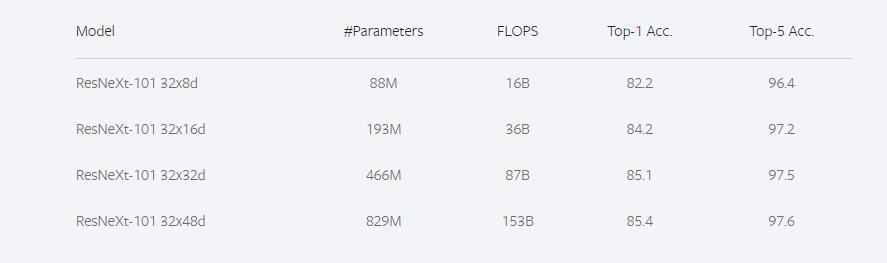
2.4 ResNeXt模型指标

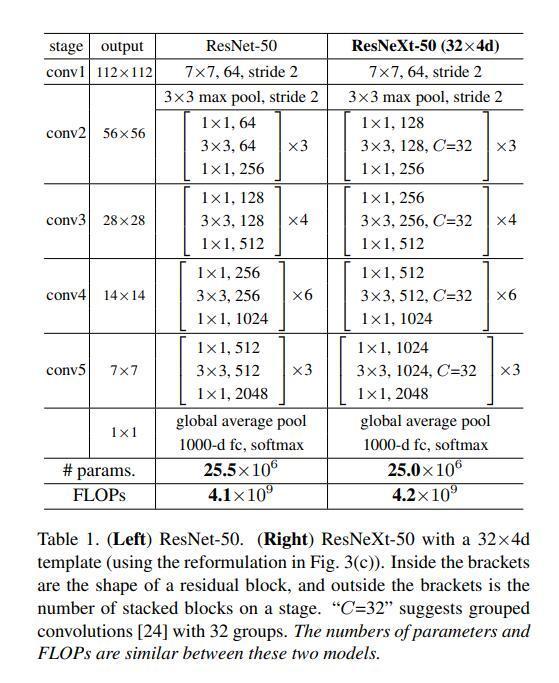
上图是ResNet与ResNeXt的参数对比，可以看出，ResNeXt与ResNet几乎是一模一样的参数量和计算量，然而两者在ImageNet上的表现却不一样。

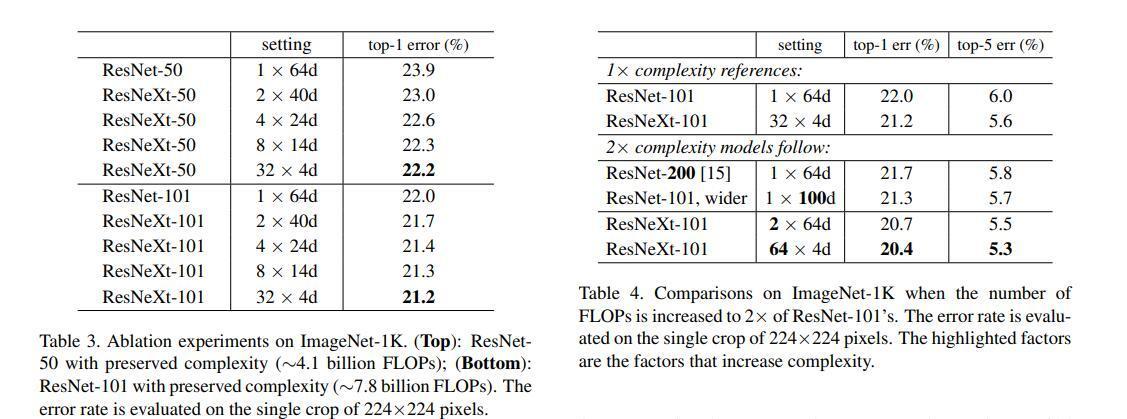
从图中可以看出，ResNeXt除了可以增加block中3×3卷积核的通道数，还可以增加cardinality的分支数来提升模型的精度。ResNeXt-50和ResNeXt-101都大大降低了对应ResNet的错误率。图中，ResNeXt-101从32×4d变为64×4d，虽然增加了两倍的计算量，但也能有效地降低分类错误率。

在2019年何凯明团队开源了ResNeXt_WSL，ResNeXt_WSL是何凯明团队使用弱监督学习训练的ResNeXt，ResNeXt_WSL中的WSL就表示Weakly Supervised Learning（弱监督学习)。

ResNeXt101_32×48d_WSL有8亿+的参数，是通过弱监督学习预训练的方法在Instagram数据集上训练，然后用ImageNet数据集做微调，Instagram有9.4亿张图片，没有经过特别的标注，只带着用户自己加的话题标签。
ResNeXt_WSL与ResNeXt是一样的结构，只是训练方式有所改变。下图是ResNeXt_WSL的训练效果。

1. 参考文献
  ResNet

ResNeXt

GoogLeNet

3.Res2Net（2020）

2020年，南开大学程明明组提出了一种面向目标检测任务的新模块Res2Net。并且其论文已被TPAMI2020录用。Res2Net和ResNeXt一样，是ResNet的变体形式，只不过Res2Net不止提高了分类任务的准确率，还提高了检测任务的精度。Res2Net的新模块可以和现有其他优秀模块轻松整合，在不增加计算负载量的情况下，在ImageNet、CIFAR-100等数据集上的测试性能超过了ResNet。因为模型的残差块里又有残差连接，所以取名为Res2Net。

3.1 Res2Net模型结构

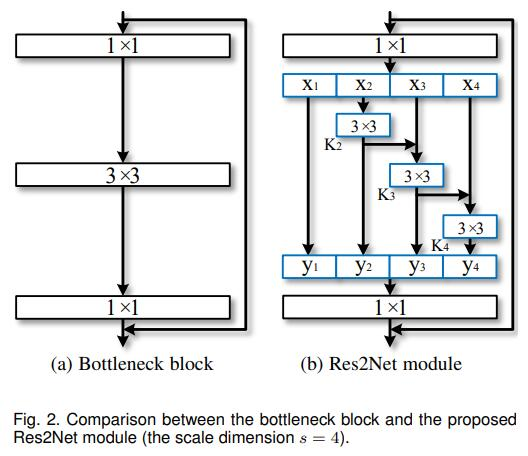
模型结构看起来很简单，将输入的特征x，split为k个特征，第i+1（i = 0， 1， 2,…,k-1) 个特征经过3×3卷积后以残差连接的方式融合到第 i+2 个特征中。这就是Res2Net的主要结构。那么这样做的目的是为什么呢？能够有什么好处呢？
答案就是多尺度卷积。多尺度特征在检测任务中一直是很重要的，自从空洞卷积提出以来，基于空洞卷积搭建的多尺度金字塔模型在检测任务上取得里程碑式的效果。不同感受野下获取的物体的信息是不同的，小的感受野可能会看到更多的物体细节，对于检测小目标也有很大的好处，而大的感受野可以感受物体的整体结构，方便网络定位物体的位置，细节与位置的结合可以更好地得到具有清晰边界的物体信息，因此，结合了多尺度金字塔的模型往往能获得很好地效果。在Res2Net中，特征k2经过3×3卷积后被送入x3所在的处理流中，k2再次被3×3的卷积优化信息，两个3×3的卷积相当于一个5×5的卷积。那么，k3就想当然与融合了3×3的感受野和5×5的感受野处理后的特征。以此类推，7×7的感受野被应用在k4中。就这样，Res2Net提取多尺度特征用于检测任务，以提高模型的准确率。在这篇论文中，s是比例尺寸的控制参数，也就是可以将输入通道数平均等分为多个特征通道。s越大表明多尺度能力越强，此外一些额外的计算开销也可以忽略。

3.2 Res2Net模型实现

Res2Net与ResNet的模型结构一致，主要差别在于block的搭建，因此这里用paddle框架来实现block的代码

class ConvBNLayer(nn.Layer):
    def __init__(
            self,
            num_channels,
            num_filters,
            filter_size,
            stride=1,
            groups=1,
            is_vd_mode=False,
            act=None,
            name=None, ):
        super(ConvBNLayer, self).__init__()
    self<span class="token punctuation">.</span>is_vd_mode <span class="token operator">=</span> is_vd_mode
    self<span class="token punctuation">.</span>_pool2d_avg <span class="token operator">=</span> AvgPool2D<span class="token punctuation">(</span>
        kernel_size<span class="token operator">=</span><span class="token number">2</span><span class="token punctuation">,</span> stride<span class="token operator">=</span><span class="token number">2</span><span class="token punctuation">,</span> padding<span class="token operator">=</span><span class="token number">0</span><span class="token punctuation">,</span> ceil_mode<span class="token operator">=</span><span class="token boolean">True</span><span class="token punctuation">)</span>
    self<span class="token punctuation">.</span>_conv <span class="token operator">=</span> Conv2D<span class="token punctuation">(</span>
        in_channels<span class="token operator">=</span>num_channels<span class="token punctuation">,</span>
        out_channels<span class="token operator">=</span>num_filters<span class="token punctuation">,</span>
        kernel_size<span class="token operator">=</span>filter_size<span class="token punctuation">,</span>
        stride<span class="token operator">=</span>stride<span class="token punctuation">,</span>
        padding<span class="token operator">=</span><span class="token punctuation">(</span>filter_size <span class="token operator">-</span> <span class="token number">1</span><span class="token punctuation">)</span> <span class="token operator">//</span> <span class="token number">2</span><span class="token punctuation">,</span>
        groups<span class="token operator">=</span>groups<span class="token punctuation">,</span>
        weight_attr<span class="token operator">=</span>ParamAttr<span class="token punctuation">(</span>name<span class="token operator">=</span>name <span class="token operator">+</span> <span class="token string">"_weights"</span><span class="token punctuation">)</span><span class="token punctuation">,</span>
        bias_attr<span class="token operator">=</span><span class="token boolean">False</span><span class="token punctuation">)</span>
    <span class="token keyword">if</span> name <span class="token operator">==</span> <span class="token string">"conv1"</span><span class="token punctuation">:</span>
        bn_name <span class="token operator">=</span> <span class="token string">"bn_"</span> <span class="token operator">+</span> name
    <span class="token keyword">else</span><span class="token punctuation">:</span>
        bn_name <span class="token operator">=</span> <span class="token string">"bn"</span> <span class="token operator">+</span> name<span class="token punctuation">[</span><span class="token number">3</span><span class="token punctuation">:</span><span class="token punctuation">]</span>
    self<span class="token punctuation">.</span>_batch_norm <span class="token operator">=</span> BatchNorm<span class="token punctuation">(</span>
        num_filters<span class="token punctuation">,</span>
        act<span class="token operator">=</span>act<span class="token punctuation">,</span>
        param_attr<span class="token operator">=</span>ParamAttr<span class="token punctuation">(</span>name<span class="token operator">=</span>bn_name <span class="token operator">+</span> <span class="token string">'_scale'</span><span class="token punctuation">)</span><span class="token punctuation">,</span>
        bias_attr<span class="token operator">=</span>ParamAttr<span class="token punctuation">(</span>bn_name <span class="token operator">+</span> <span class="token string">'_offset'</span><span class="token punctuation">)</span><span class="token punctuation">,</span>
        moving_mean_name<span class="token operator">=</span>bn_name <span class="token operator">+</span> <span class="token string">'_mean'</span><span class="token punctuation">,</span>
        moving_variance_name<span class="token operator">=</span>bn_name <span class="token operator">+</span> <span class="token string">'_variance'</span><span class="token punctuation">)</span>

<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> inputs<span class="token punctuation">)</span><span class="token punctuation">:</span>
    <span class="token keyword">if</span> self<span class="token punctuation">.</span>is_vd_mode<span class="token punctuation">:</span>
        inputs <span class="token operator">=</span> self<span class="token punctuation">.</span>_pool2d_avg<span class="token punctuation">(</span>inputs<span class="token punctuation">)</span>
    y <span class="token operator">=</span> self<span class="token punctuation">.</span>_conv<span class="token punctuation">(</span>inputs<span class="token punctuation">)</span>
    y <span class="token operator">=</span> self<span class="token punctuation">.</span>_batch_norm<span class="token punctuation">(</span>y<span class="token punctuation">)</span>
    <span class="token keyword">return</span> y

class BottleneckBlock(nn.Layer):
def init(self,
num_channels1,
num_channels2,
num_filters,
stride,
scales,
shortcut=True,
if_first=False,
name=None):
super(BottleneckBlock, self).init()
self.stride = stride
self.scales = scales
self.conv0 = ConvBNLayer(
num_channels=num_channels1,
num_filters=num_filters,
filter_size=1,
act=‘relu’,
name=name + “_branch2a”)
self.conv1_list = []
for s in range(scales - 1):
conv1 = self.add_sublayer(
name + ‘branch2b’ + str(s + 1),
ConvBNLayer(
num_channels=num_filters // scales,
num_filters=num_filters // scales,
filter_size=3,
stride=stride,
act=‘relu’,
name=name + ‘branch2b’ + str(s + 1)))
self.conv1_list.append(conv1)
self.pool2d_avg = AvgPool2D(kernel_size=3, stride=stride, padding=1)

    self<span class="token punctuation">.</span>conv2 <span class="token operator">=</span> ConvBNLayer<span class="token punctuation">(</span>
        num_channels<span class="token operator">=</span>num_filters<span class="token punctuation">,</span>
        num_filters<span class="token operator">=</span>num_channels2<span class="token punctuation">,</span>
        filter_size<span class="token operator">=</span><span class="token number">1</span><span class="token punctuation">,</span>
        act<span class="token operator">=</span><span class="token boolean">None</span><span class="token punctuation">,</span>
        name<span class="token operator">=</span>name <span class="token operator">+</span> <span class="token string">"_branch2c"</span><span class="token punctuation">)</span>

    <span class="token keyword">if</span> <span class="token keyword">not</span> shortcut<span class="token punctuation">:</span>
        self<span class="token punctuation">.</span>short <span class="token operator">=</span> ConvBNLayer<span class="token punctuation">(</span>
            num_channels<span class="token operator">=</span>num_channels1<span class="token punctuation">,</span>
            num_filters<span class="token operator">=</span>num_channels2<span class="token punctuation">,</span>
            filter_size<span class="token operator">=</span><span class="token number">1</span><span class="token punctuation">,</span>
            stride<span class="token operator">=</span><span class="token number">1</span><span class="token punctuation">,</span>
            is_vd_mode<span class="token operator">=</span><span class="token boolean">False</span> <span class="token keyword">if</span> if_first <span class="token keyword">else</span> <span class="token boolean">True</span><span class="token punctuation">,</span>
            name<span class="token operator">=</span>name <span class="token operator">+</span> <span class="token string">"_branch1"</span><span class="token punctuation">)</span>

    self<span class="token punctuation">.</span>shortcut <span class="token operator">=</span> shortcut

<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> inputs<span class="token punctuation">)</span><span class="token punctuation">:</span>
    y <span class="token operator">=</span> self<span class="token punctuation">.</span>conv0<span class="token punctuation">(</span>inputs<span class="token punctuation">)</span>
    xs <span class="token operator">=</span> paddle<span class="token punctuation">.</span>split<span class="token punctuation">(</span>y<span class="token punctuation">,</span> self<span class="token punctuation">.</span>scales<span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">)</span>
    ys <span class="token operator">=</span> <span class="token punctuation">[</span><span class="token punctuation">]</span>
    <span class="token keyword">for</span> s<span class="token punctuation">,</span> conv1 <span class="token keyword">in</span> <span class="token builtin">enumerate</span><span class="token punctuation">(</span>self<span class="token punctuation">.</span>conv1_list<span class="token punctuation">)</span><span class="token punctuation">:</span>
        <span class="token keyword">if</span> s <span class="token operator">==</span> <span class="token number">0</span> <span class="token keyword">or</span> self<span class="token punctuation">.</span>stride <span class="token operator">==</span> <span class="token number">2</span><span class="token punctuation">:</span>
            ys<span class="token punctuation">.</span>append<span class="token punctuation">(</span>conv1<span class="token punctuation">(</span>xs<span class="token punctuation">[</span>s<span class="token punctuation">]</span><span class="token punctuation">)</span><span class="token punctuation">)</span>
        <span class="token keyword">else</span><span class="token punctuation">:</span>
            ys<span class="token punctuation">.</span>append<span class="token punctuation">(</span>conv1<span class="token punctuation">(</span>xs<span class="token punctuation">[</span>s<span class="token punctuation">]</span> <span class="token operator">+</span> ys<span class="token punctuation">[</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">)</span><span class="token punctuation">)</span>
    <span class="token keyword">if</span> self<span class="token punctuation">.</span>stride <span class="token operator">==</span> <span class="token number">1</span><span class="token punctuation">:</span>
        ys<span class="token punctuation">.</span>append<span class="token punctuation">(</span>xs<span class="token punctuation">[</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">)</span>
    <span class="token keyword">else</span><span class="token punctuation">:</span>
        ys<span class="token punctuation">.</span>append<span class="token punctuation">(</span>self<span class="token punctuation">.</span>pool2d_avg<span class="token punctuation">(</span>xs<span class="token punctuation">[</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">)</span><span class="token punctuation">)</span>
    conv1 <span class="token operator">=</span> paddle<span class="token punctuation">.</span>concat<span class="token punctuation">(</span>ys<span class="token punctuation">,</span> axis<span class="token operator">=</span><span class="token number">1</span><span class="token punctuation">)</span>
    conv2 <span class="token operator">=</span> self<span class="token punctuation">.</span>conv2<span class="token punctuation">(</span>conv1<span class="token punctuation">)</span>

    <span class="token keyword">if</span> self<span class="token punctuation">.</span>shortcut<span class="token punctuation">:</span>
        short <span class="token operator">=</span> inputs
    <span class="token keyword">else</span><span class="token punctuation">:</span>
        short <span class="token operator">=</span> self<span class="token punctuation">.</span>short<span class="token punctuation">(</span>inputs<span class="token punctuation">)</span>
    y <span class="token operator">=</span> paddle<span class="token punctuation">.</span>add<span class="token punctuation">(</span>x<span class="token operator">=</span>short<span class="token punctuation">,</span> y<span class="token operator">=</span>conv2<span class="token punctuation">)</span>
    y <span class="token operator">=</span> F<span class="token punctuation">.</span>relu<span class="token punctuation">(</span>y<span class="token punctuation">)</span>
    <span class="token keyword">return</span> y

3.3 模型特点

可与其他结构整合，如SENEt， ResNeXt， DLA等，从而增加准确率。
计算负载不增加，特征提取能力更强大。

3.4 模型指标

ImageNet分类效果如下图

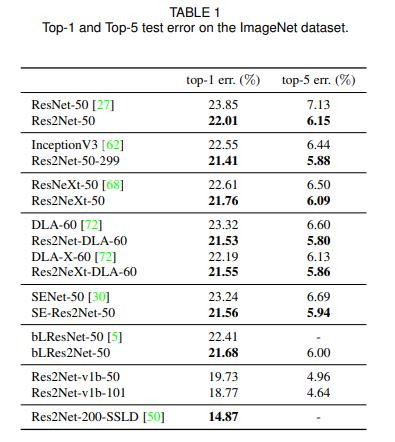
Res2Net-50就是对标ResNet50的版本。

Res2Net-50-299指的是将输入图片裁剪到299×299进行预测的Res2Net-50，因为一般都是裁剪或者resize到224×224。

Res2NeXt-50为融合了ResNeXt的Res2Net-50。

Res2Net-DLA-60指的是融合了DLA-60的Res2Net-50。

Res2NeXt-DLA-60为融合了ResNeXt和DLA-60的Res2Net-50。

SE-Res2Net-50 为融合了SENet的Res2Net-50。

blRes2Net-50为融合了Big-Little Net的Res2Net-50。

Res2Net-v1b-50为采取和ResNet-vd-50一样的处理方法的Res2Net-50。

Res2Net-200-SSLD为Paddle使用简单的半监督标签知识蒸馏（SSLD，Simple Semi-supervised Label Distillation）的方法来提升模型效果得到的。

可见，Res2Net都取得了十分不错的成绩。

COCO数据集效果如下图

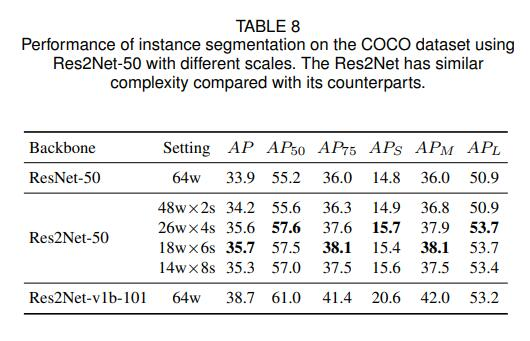
Res2Net-50的各种配置都比ResNet-50高。

显著目标检测数据集指标效果如下图

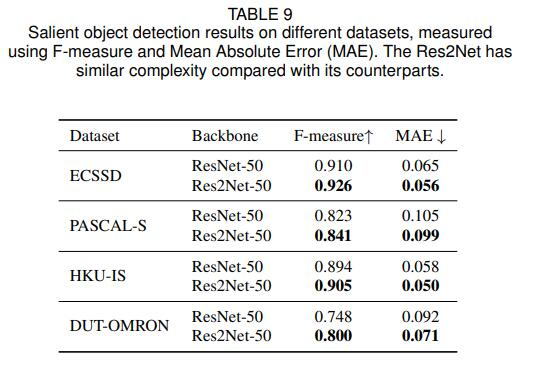
ECSSD、PASCAL-S、DUT-OMRON、HKU-IS都是显著目标检测任务中现在最为常用的测试集，显著目标检测任务的目的就是分割出图片中的显著物体，并用白色像素点表示，其他背景用黑色像素点表示。从图中可以看出来，使用Res2Net作为骨干网络，效果比ResNet有了很大的提升。

参考文献
Res2Net

4.Swin Trasnformer（2021）

Swin Transformer是由微软亚洲研究院在今年公布的一篇利用transformer架构处理计算机视觉任务的论文。Swin Transformer 在图像分类，图像分割，目标检测等各个领域已经屠榜，在论文中，作者分析表明，Transformer从NLP迁移到CV上没有大放异彩主要有两点原因：1. 两个领域涉及的scale不同，NLP的token是标准固定的大小，而CV的特征尺度变化范围非常大。2. CV比起NLP需要更大的分辨率，而且CV中使用Transformer的计算复杂度是图像尺度的平方，这会导致计算量过于庞大。为了解决这两个问题，Swin Transformer相比之前的ViT做了两个改进：1.引入CNN中常用的层次化构建方式构建层次化Transformer 2.引入locality思想，对无重合的window区域内进行self-attention计算。另外，Swin Transformer可以作为图像分类、目标检测和语义分割等任务的通用骨干网络，可以说，Swin Transformer可能是CNN的完美替代方案。

4.1 Swin Trasnformer模型结构

下图为Swin Transformer与ViT在处理图片方式上的对比，可以看出，Swin Transformer有着ResNet一样的残差结构和CNN具有的多尺度图片结构。

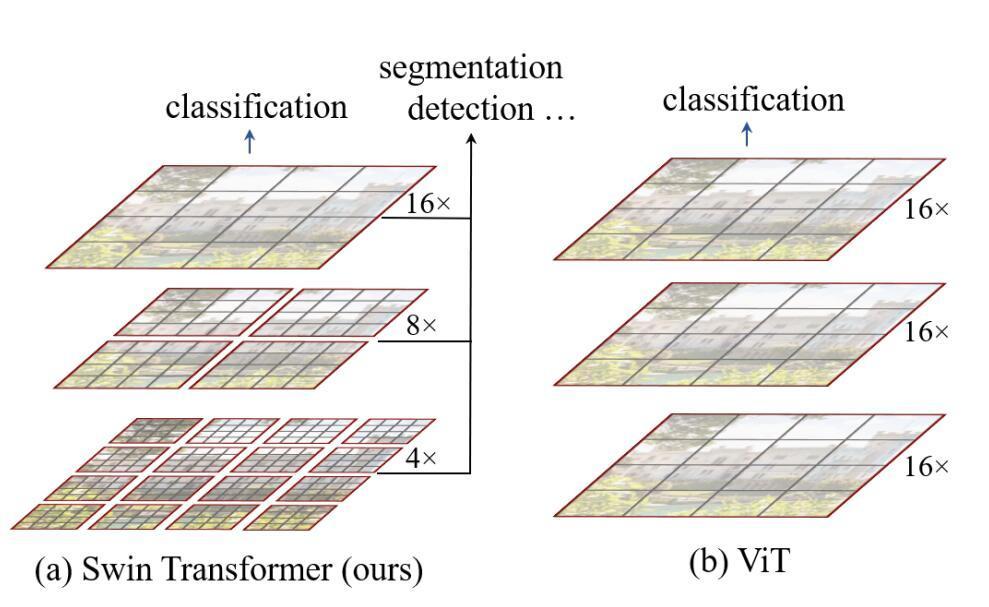
整体概括：

下图为Swin Transformer的网络结构，输入的图像先经过一层卷积进行patch映射，将图像先分割成4 × 4的小块，图片是224×224输入，那么就是56个path块，如果是384×384的尺寸，则是96个path块。这里以224 × 224的输入为例，输入图像经过这一步操作，每个patch的特征维度为4x4x3=48的特征图。因此，输入的图像变成了H/4×W/4×48的特征图。然后，特征图开始输入到stage1，stage1中linear embedding将path特征维度变成C，因此变成了H/4×W/4×C。然后送入Swin Transformer Block，在进入stage2前，接下来先通过Patch Merging操作，Patch Merging和CNN中stride=2的1×1卷积十分相似，Patch Merging在每个Stage开始前做降采样，用于缩小分辨率，调整通道数，当H/4×W/4×C的特征图输送到Patch Merging，将输入按照2x2的相邻patches合并，这样子patch块的数量就变成了H/8 x W/8，特征维度就变成了4C，之后经过一个MLP，将特征维度降为2C。因此变为H/8×W/8×2C。接下来的stage就是重复上面的过程。

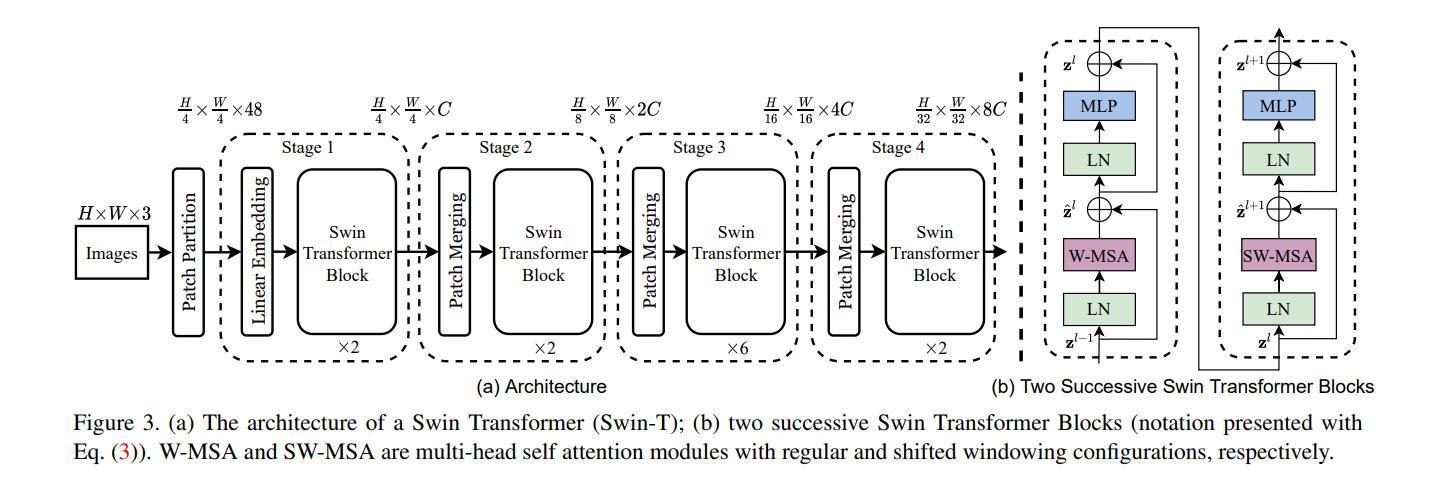
每步细说：

Linear embedding

下面用Paddle代码逐步讲解Swin Transformer的架构。以下代码为Linear embedding的操作，整个操作可以看作一个patch大小的卷积核和patch大小的步长的卷积对输入的B，C，H，W的图片进行卷积，得到的自然就是大小为 B，C，H/patch，W/patch的特征图，如果放在第一个Linear embedding中，得到的特征图就为 B，96，56，56的大小。Paddle核心代码如下。

class PatchEmbed(nn.Layer):
    """ Image to Patch Embedding
    Args:
        img_size (int): Image size.  Default: 224.
        patch_size (int): Patch token size. Default: 4.
        in_chans (int): Number of input image channels. Default: 3.
        embed_dim (int): Number of linear projection output channels. Default: 96.
        norm_layer (nn.Layer, optional): Normalization layer. Default: None
    """
<span class="token keyword">def</span> <span class="token function">__init__</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span>
             img_size<span class="token operator">=</span><span class="token number">224</span><span class="token punctuation">,</span>
             patch_size<span class="token operator">=</span><span class="token number">4</span><span class="token punctuation">,</span>
             in_chans<span class="token operator">=</span><span class="token number">3</span><span class="token punctuation">,</span>
             embed_dim<span class="token operator">=</span><span class="token number">96</span><span class="token punctuation">,</span>
             norm_layer<span class="token operator">=</span><span class="token boolean">None</span><span class="token punctuation">)</span><span class="token punctuation">:</span>
    <span class="token builtin">super</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">.</span>__init__<span class="token punctuation">(</span><span class="token punctuation">)</span>
    img_size <span class="token operator">=</span> to_2tuple<span class="token punctuation">(</span>img_size<span class="token punctuation">)</span>
    patch_size <span class="token operator">=</span> to_2tuple<span class="token punctuation">(</span>patch_size<span class="token punctuation">)</span>
    patches_resolution <span class="token operator">=</span> <span class="token punctuation">[</span>
        img_size<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span> <span class="token operator">//</span> patch_size<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span><span class="token punctuation">,</span> img_size<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span> <span class="token operator">//</span> patch_size<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span>
    <span class="token punctuation">]</span>
    self<span class="token punctuation">.</span>img_size <span class="token operator">=</span> img_size
    self<span class="token punctuation">.</span>patch_size <span class="token operator">=</span> patch_size
    self<span class="token punctuation">.</span>patches_resolution <span class="token operator">=</span> patches_resolution
    self<span class="token punctuation">.</span>num_patches <span class="token operator">=</span> patches_resolution<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span> <span class="token operator">*</span> patches_resolution<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span> <span class="token comment">#patch个数</span>

    self<span class="token punctuation">.</span>in_chans <span class="token operator">=</span> in_chans
    self<span class="token punctuation">.</span>embed_dim <span class="token operator">=</span> embed_dim

    self<span class="token punctuation">.</span>proj <span class="token operator">=</span> nn<span class="token punctuation">.</span>Conv2D<span class="token punctuation">(</span>
        in_chans<span class="token punctuation">,</span> embed_dim<span class="token punctuation">,</span> kernel_size<span class="token operator">=</span>patch_size<span class="token punctuation">,</span> stride<span class="token operator">=</span>patch_size<span class="token punctuation">)</span> <span class="token comment">#将stride和kernel_size设置为patch_size大小</span>
    <span class="token keyword">if</span> norm_layer <span class="token keyword">is</span> <span class="token keyword">not</span> <span class="token boolean">None</span><span class="token punctuation">:</span>
        self<span class="token punctuation">.</span>norm <span class="token operator">=</span> norm_layer<span class="token punctuation">(</span>embed_dim<span class="token punctuation">)</span>
    <span class="token keyword">else</span><span class="token punctuation">:</span>
        self<span class="token punctuation">.</span>norm <span class="token operator">=</span> <span class="token boolean">None</span>

<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> x<span class="token punctuation">)</span><span class="token punctuation">:</span>
    B<span class="token punctuation">,</span> C<span class="token punctuation">,</span> H<span class="token punctuation">,</span> W <span class="token operator">=</span> x<span class="token punctuation">.</span>shape
    
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>proj<span class="token punctuation">(</span>x<span class="token punctuation">)</span> <span class="token comment"># B, 96, H/4, W4 </span>

    x <span class="token operator">=</span> x<span class="token punctuation">.</span>flatten<span class="token punctuation">(</span><span class="token number">2</span><span class="token punctuation">)</span><span class="token punctuation">.</span>transpose<span class="token punctuation">(</span><span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">,</span> <span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">)</span>  <span class="token comment"># B Ph*Pw 96</span>
    <span class="token keyword">if</span> self<span class="token punctuation">.</span>norm <span class="token keyword">is</span> <span class="token keyword">not</span> <span class="token boolean">None</span><span class="token punctuation">:</span>
        x <span class="token operator">=</span> self<span class="token punctuation">.</span>norm<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token keyword">return</span> x

Patch Merging

以下为PatchMerging的操作。该操作以2为步长，对输入的图片进行采样，总共得到4张下采样的特征图，H和W降低2倍，因此，通道级拼接后得到的是B，4C，H/2，W/2的特征图。然而这样的拼接不能够提取有用的特征信息，于是，一个线性层将4C的通道筛选为2C, 特征图变为了B，2C， H/2， W/2。细细体会可以发现，该操作像极了
卷积常用的Pooling操作和步长为2的卷积操作。Poling用于下采样，步长为2的卷积同样可以下采样，另外还起到了特征筛选的效果。总结一下，经过这个操作原本B，C，H，W的特征图就变为了B，2C，H/2，W/2的特征图，完成了下采样操作。

class PatchMerging(nn.Layer):
    r""" Patch Merging Layer.
    Args:
        input_resolution (tuple[int]): Resolution of input feature.
        dim (int): Number of input channels.
        norm_layer (nn.Layer, optional): Normalization layer.  Default: nn.LayerNorm
    """
<span class="token keyword">def</span> <span class="token function">__init__</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> input_resolution<span class="token punctuation">,</span> dim<span class="token punctuation">,</span> norm_layer<span class="token operator">=</span>nn<span class="token punctuation">.</span>LayerNorm<span class="token punctuation">)</span><span class="token punctuation">:</span>
    <span class="token builtin">super</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">.</span>__init__<span class="token punctuation">(</span><span class="token punctuation">)</span>
    self<span class="token punctuation">.</span>input_resolution <span class="token operator">=</span> input_resolution
    self<span class="token punctuation">.</span>dim <span class="token operator">=</span> dim
    self<span class="token punctuation">.</span>reduction <span class="token operator">=</span> nn<span class="token punctuation">.</span>Linear<span class="token punctuation">(</span><span class="token number">4</span> <span class="token operator">*</span> dim<span class="token punctuation">,</span> <span class="token number">2</span> <span class="token operator">*</span> dim<span class="token punctuation">,</span> bias_attr<span class="token operator">=</span><span class="token boolean">False</span><span class="token punctuation">)</span>
    self<span class="token punctuation">.</span>norm <span class="token operator">=</span> norm_layer<span class="token punctuation">(</span><span class="token number">4</span> <span class="token operator">*</span> dim<span class="token punctuation">)</span>

<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> x<span class="token punctuation">)</span><span class="token punctuation">:</span>
    <span class="token triple-quoted-string string">"""
    x: B, H*W, C
    """</span>
    H<span class="token punctuation">,</span> W <span class="token operator">=</span> self<span class="token punctuation">.</span>input_resolution
    B<span class="token punctuation">,</span> L<span class="token punctuation">,</span> C <span class="token operator">=</span> x<span class="token punctuation">.</span>shape
    <span class="token keyword">assert</span> L <span class="token operator">==</span> H <span class="token operator">*</span> W<span class="token punctuation">,</span> <span class="token string">"input feature has wrong size"</span>
    <span class="token keyword">assert</span> H <span class="token operator">%</span> <span class="token number">2</span> <span class="token operator">==</span> <span class="token number">0</span> <span class="token keyword">and</span> W <span class="token operator">%</span> <span class="token number">2</span> <span class="token operator">==</span> <span class="token number">0</span><span class="token punctuation">,</span> <span class="token string">"x size ({}*{}) are not even."</span><span class="token punctuation">.</span><span class="token builtin">format</span><span class="token punctuation">(</span>
        H<span class="token punctuation">,</span> W<span class="token punctuation">)</span>

    x <span class="token operator">=</span> x<span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span>B<span class="token punctuation">,</span> H<span class="token punctuation">,</span> W<span class="token punctuation">,</span> C<span class="token punctuation">]</span><span class="token punctuation">)</span>
    <span class="token comment"># 每次降采样是两倍，因此在行方向和列方向上，间隔2选取元素。</span>
    x0 <span class="token operator">=</span> x<span class="token punctuation">[</span><span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">:</span><span class="token punctuation">:</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">:</span><span class="token punctuation">:</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token punctuation">:</span><span class="token punctuation">]</span>  <span class="token comment"># B H/2 W/2 C</span>
    x1 <span class="token operator">=</span> x<span class="token punctuation">[</span><span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">:</span><span class="token punctuation">:</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">:</span><span class="token punctuation">:</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token punctuation">:</span><span class="token punctuation">]</span>  <span class="token comment"># B H/2 W/2 C</span>
    x2 <span class="token operator">=</span> x<span class="token punctuation">[</span><span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">:</span><span class="token punctuation">:</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">:</span><span class="token punctuation">:</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token punctuation">:</span><span class="token punctuation">]</span>  <span class="token comment"># B H/2 W/2 C</span>
    x3 <span class="token operator">=</span> x<span class="token punctuation">[</span><span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">:</span><span class="token punctuation">:</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">:</span><span class="token punctuation">:</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token punctuation">:</span><span class="token punctuation">]</span>  <span class="token comment"># B H/2 W/2 C</span>
    <span class="token comment"># 拼接在一起作为一整个张量，展开。通道维度会变成原先的4倍（因为H,W各缩小2倍）</span>
    x <span class="token operator">=</span> paddle<span class="token punctuation">.</span>concat<span class="token punctuation">(</span><span class="token punctuation">[</span>x0<span class="token punctuation">,</span> x1<span class="token punctuation">,</span> x2<span class="token punctuation">,</span> x3<span class="token punctuation">]</span><span class="token punctuation">,</span> <span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">)</span>  <span class="token comment"># B H/2 W/2 4*C</span>
    x <span class="token operator">=</span> x<span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span>B<span class="token punctuation">,</span> H <span class="token operator">*</span> W <span class="token operator">//</span> <span class="token number">4</span><span class="token punctuation">,</span> <span class="token number">4</span> <span class="token operator">*</span> C<span class="token punctuation">]</span><span class="token punctuation">)</span>  <span class="token comment"># B H/2*W/2 4*C </span>

    x <span class="token operator">=</span> self<span class="token punctuation">.</span>norm<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token comment"># 通过一个全连接层再调整通道维度为原来的两倍</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>reduction<span class="token punctuation">(</span>x<span class="token punctuation">)</span>

    <span class="token keyword">return</span> x

Swin Transformer Block：

下面的操作是根据window_size划分特征图的操作和还原的操作，原理很简单就是并排划分即可。

def window_partition(x, window_size):
    """
    Args:
        x: (B, H, W, C)
        window_size (int): window size
Returns:
    windows: (num_windows*B, window_size, window_size, C)
"""</span>
B<span class="token punctuation">,</span> H<span class="token punctuation">,</span> W<span class="token punctuation">,</span> C <span class="token operator">=</span> x<span class="token punctuation">.</span>shape
x <span class="token operator">=</span> x<span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span>B<span class="token punctuation">,</span> H <span class="token operator">//</span> window_size<span class="token punctuation">,</span> window_size<span class="token punctuation">,</span> W <span class="token operator">//</span> window_size<span class="token punctuation">,</span> window_size<span class="token punctuation">,</span> C<span class="token punctuation">]</span><span class="token punctuation">)</span>
windows <span class="token operator">=</span> x<span class="token punctuation">.</span>transpose<span class="token punctuation">(</span><span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">,</span> <span class="token number">3</span><span class="token punctuation">,</span> <span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">4</span><span class="token punctuation">,</span> <span class="token number">5</span><span class="token punctuation">]</span><span class="token punctuation">)</span><span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">,</span> window_size<span class="token punctuation">,</span> window_size<span class="token punctuation">,</span> C<span class="token punctuation">]</span><span class="token punctuation">)</span>
<span class="token keyword">return</span> windows

def window_reverse(windows, window_size, H, W):
“”"
Args:
windows: (num_windows*B, window_size, window_size, C)
window_size (int): Window size
H (int): Height of image
W (int): Width of image

Returns:
    x: (B, H, W, C)
"""</span>
B <span class="token operator">=</span> <span class="token builtin">int</span><span class="token punctuation">(</span>windows<span class="token punctuation">.</span>shape<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span> <span class="token operator">/</span> <span class="token punctuation">(</span>H <span class="token operator">*</span> W <span class="token operator">/</span> window_size <span class="token operator">/</span> window_size<span class="token punctuation">)</span><span class="token punctuation">)</span>
x <span class="token operator">=</span> windows<span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span>B<span class="token punctuation">,</span> H <span class="token operator">//</span> window_size<span class="token punctuation">,</span> W <span class="token operator">//</span> window_size<span class="token punctuation">,</span> window_size<span class="token punctuation">,</span> window_size<span class="token punctuation">,</span> <span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">)</span>
x <span class="token operator">=</span> x<span class="token punctuation">.</span>transpose<span class="token punctuation">(</span><span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">,</span> <span class="token number">3</span><span class="token punctuation">,</span> <span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">4</span><span class="token punctuation">,</span> <span class="token number">5</span><span class="token punctuation">]</span><span class="token punctuation">)</span><span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span>B<span class="token punctuation">,</span> H<span class="token punctuation">,</span> W<span class="token punctuation">,</span> <span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">)</span>
<span class="token keyword">return</span> x

Swin Transformer中重要的当然是Swin Transformer Block了，下面解释一下Swin Transformer Block的原理。
先看一下MLP和LN，MLP和LN为多层感知机和相对于BatchNorm的LayerNorm。原理较为简单，因此直接看paddle代码即可。

class Mlp(nn.Layer):
    def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
        super().__init__()
        out_features = out_features or in_features
        hidden_features = hidden_features or in_features
        self.fc1 = nn.Linear(in_features, hidden_features)
        self.act = act_layer()
        self.fc2 = nn.Linear(hidden_features, out_features)
        self.drop = nn.Dropout(drop)
<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> x<span class="token punctuation">)</span><span class="token punctuation">:</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>fc1<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>act<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>drop<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>fc2<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>drop<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token keyword">return</span> x

下图就是Shifted Window based MSA是Swin Transformer的核心部分。Shifted Window based MSA包括了两部分，一个是W-MSA（窗口多头注意力），另一个就是SW-MSA（移位窗口多头自注意力）。这两个是一同出现的。

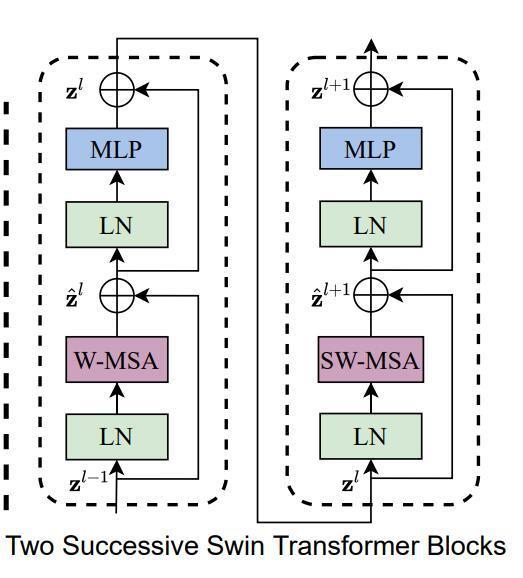
一开始，Swin Transformer 将一张图片分割为4份，也叫4个Window，然后独立地计算每一部分的MSA。由于每一个Window都是独立的，缺少了信息之间的交流，因此作者又提出了SW-MSA的算法，即采用规则的移动窗口的方法。通过不同窗口的交互，来达到特征的信息交流。注意，这一部分是本论文的精华，想要了解的同学必须要看懂源代码

class WindowAttention(nn.Layer):
    """ Window based multi-head self attention (W-MSA) module with relative position bias.
    It supports both of shifted and non-shifted window.
Args:
    dim (int): Number of input channels.
    window_size (tuple[int]): The height and width of the window.
    num_heads (int): Number of attention heads.
    qkv_bias (bool, optional):  If True, add a learnable bias to query, key, value. Default: True
    qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set
    attn_drop (float, optional): Dropout ratio of attention weight. Default: 0.0
    proj_drop (float, optional): Dropout ratio of output. Default: 0.0
"""</span>

<span class="token keyword">def</span> <span class="token function">__init__</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> dim<span class="token punctuation">,</span> window_size<span class="token punctuation">,</span> num_heads<span class="token punctuation">,</span> qkv_bias<span class="token operator">=</span><span class="token boolean">True</span><span class="token punctuation">,</span> qk_scale<span class="token operator">=</span><span class="token boolean">None</span><span class="token punctuation">,</span> attn_drop<span class="token operator">=</span><span class="token number">0.</span><span class="token punctuation">,</span> proj_drop<span class="token operator">=</span><span class="token number">0.</span><span class="token punctuation">)</span><span class="token punctuation">:</span>

    <span class="token builtin">super</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">.</span>__init__<span class="token punctuation">(</span><span class="token punctuation">)</span>
    self<span class="token punctuation">.</span>dim <span class="token operator">=</span> dim
    self<span class="token punctuation">.</span>window_size <span class="token operator">=</span> window_size  <span class="token comment"># Wh, Ww</span>
    self<span class="token punctuation">.</span>num_heads <span class="token operator">=</span> num_heads
    head_dim <span class="token operator">=</span> dim <span class="token operator">//</span> num_heads
    self<span class="token punctuation">.</span>scale <span class="token operator">=</span> qk_scale <span class="token keyword">or</span> head_dim <span class="token operator">**</span> <span class="token operator">-</span><span class="token number">0.5</span>

    <span class="token comment"># define a parameter table of relative position bias</span>
    relative_position_bias_table <span class="token operator">=</span> self<span class="token punctuation">.</span>create_parameter<span class="token punctuation">(</span>
        shape<span class="token operator">=</span><span class="token punctuation">(</span><span class="token punctuation">(</span><span class="token number">2</span> <span class="token operator">*</span> window_size<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span> <span class="token operator">-</span> <span class="token number">1</span><span class="token punctuation">)</span> <span class="token operator">*</span> <span class="token punctuation">(</span><span class="token number">2</span> <span class="token operator">*</span> window_size<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span> <span class="token operator">-</span> <span class="token number">1</span><span class="token punctuation">)</span><span class="token punctuation">,</span> num_heads<span class="token punctuation">)</span><span class="token punctuation">,</span> default_initializer<span class="token operator">=</span>nn<span class="token punctuation">.</span>initializer<span class="token punctuation">.</span>Constant<span class="token punctuation">(</span>value<span class="token operator">=</span><span class="token number">0</span><span class="token punctuation">)</span><span class="token punctuation">)</span>  <span class="token comment"># 2*Wh-1 * 2*Ww-1, nH</span>
    self<span class="token punctuation">.</span>add_parameter<span class="token punctuation">(</span><span class="token string">"relative_position_bias_table"</span><span class="token punctuation">,</span> relative_position_bias_table<span class="token punctuation">)</span>

    <span class="token comment"># get pair-wise relative position index for each token inside the window</span>
    coords_h <span class="token operator">=</span> paddle<span class="token punctuation">.</span>arange<span class="token punctuation">(</span>self<span class="token punctuation">.</span>window_size<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span><span class="token punctuation">)</span>
    coords_w <span class="token operator">=</span> paddle<span class="token punctuation">.</span>arange<span class="token punctuation">(</span>self<span class="token punctuation">.</span>window_size<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">)</span>
    coords <span class="token operator">=</span> paddle<span class="token punctuation">.</span>stack<span class="token punctuation">(</span>paddle<span class="token punctuation">.</span>meshgrid<span class="token punctuation">(</span><span class="token punctuation">[</span>coords_h<span class="token punctuation">,</span> coords_w<span class="token punctuation">]</span><span class="token punctuation">)</span><span class="token punctuation">)</span>                   <span class="token comment"># 2, Wh, Ww</span>
    coords_flatten <span class="token operator">=</span> paddle<span class="token punctuation">.</span>flatten<span class="token punctuation">(</span>coords<span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">)</span>                                     <span class="token comment"># 2, Wh*Ww</span>
    relative_coords <span class="token operator">=</span> coords_flatten<span class="token punctuation">.</span>unsqueeze<span class="token punctuation">(</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">)</span> <span class="token operator">-</span> coords_flatten<span class="token punctuation">.</span>unsqueeze<span class="token punctuation">(</span><span class="token number">1</span><span class="token punctuation">)</span>   <span class="token comment"># 2, Wh*Ww, Wh*Ww</span>
    relative_coords <span class="token operator">=</span> relative_coords<span class="token punctuation">.</span>transpose<span class="token punctuation">(</span><span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">,</span> <span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">]</span><span class="token punctuation">)</span>                         <span class="token comment"># Wh*Ww, Wh*Ww, 2</span>
    relative_coords<span class="token punctuation">[</span><span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">]</span> <span class="token operator">+=</span> self<span class="token punctuation">.</span>window_size<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span> <span class="token operator">-</span> <span class="token number">1</span>                            <span class="token comment"># shift to start from 0</span>
    relative_coords<span class="token punctuation">[</span><span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">]</span> <span class="token operator">+=</span> self<span class="token punctuation">.</span>window_size<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span> <span class="token operator">-</span> <span class="token number">1</span>
    relative_coords<span class="token punctuation">[</span><span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token punctuation">:</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">]</span> <span class="token operator">*=</span> <span class="token number">2</span> <span class="token operator">*</span> self<span class="token punctuation">.</span>window_size<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span> <span class="token operator">-</span> <span class="token number">1</span>
    self<span class="token punctuation">.</span>relative_position_index <span class="token operator">=</span> relative_coords<span class="token punctuation">.</span><span class="token builtin">sum</span><span class="token punctuation">(</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">)</span>                         <span class="token comment"># Wh*Ww, Wh*Ww</span>
    self<span class="token punctuation">.</span>register_buffer<span class="token punctuation">(</span><span class="token string">"relative_position_index"</span><span class="token punctuation">,</span> self<span class="token punctuation">.</span>relative_position_index<span class="token punctuation">)</span>

    self<span class="token punctuation">.</span>qkv <span class="token operator">=</span> nn<span class="token punctuation">.</span>Linear<span class="token punctuation">(</span>dim<span class="token punctuation">,</span> dim <span class="token operator">*</span> <span class="token number">3</span><span class="token punctuation">,</span> bias_attr<span class="token operator">=</span>qkv_bias<span class="token punctuation">)</span>
    self<span class="token punctuation">.</span>attn_drop <span class="token operator">=</span> nn<span class="token punctuation">.</span>Dropout<span class="token punctuation">(</span>attn_drop<span class="token punctuation">)</span>
    self<span class="token punctuation">.</span>proj <span class="token operator">=</span> nn<span class="token punctuation">.</span>Linear<span class="token punctuation">(</span>dim<span class="token punctuation">,</span> dim<span class="token punctuation">)</span>
    self<span class="token punctuation">.</span>proj_drop <span class="token operator">=</span> nn<span class="token punctuation">.</span>Dropout<span class="token punctuation">(</span>proj_drop<span class="token punctuation">)</span>

    self<span class="token punctuation">.</span>softmax <span class="token operator">=</span> nn<span class="token punctuation">.</span>Softmax<span class="token punctuation">(</span>axis<span class="token operator">=</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">)</span>

<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> x<span class="token punctuation">,</span> mask<span class="token operator">=</span><span class="token boolean">None</span><span class="token punctuation">)</span><span class="token punctuation">:</span>
    <span class="token triple-quoted-string string">"""
    Args:
        x: input features with shape of (num_windows*B, N, C)
        mask: (0/-inf) mask with shape of (num_windows, Wh*Ww, Wh*Ww) or None
    """</span>
    B_<span class="token punctuation">,</span> N<span class="token punctuation">,</span> C <span class="token operator">=</span> x<span class="token punctuation">.</span>shape
    qkv <span class="token operator">=</span> self<span class="token punctuation">.</span>qkv<span class="token punctuation">(</span>x<span class="token punctuation">)</span><span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span>B_<span class="token punctuation">,</span> N<span class="token punctuation">,</span> <span class="token number">3</span><span class="token punctuation">,</span> self<span class="token punctuation">.</span>num_heads<span class="token punctuation">,</span> C <span class="token operator">//</span> self<span class="token punctuation">.</span>num_heads<span class="token punctuation">]</span><span class="token punctuation">)</span><span class="token punctuation">.</span>transpose<span class="token punctuation">(</span><span class="token punctuation">[</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">,</span> <span class="token number">3</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">,</span> <span class="token number">4</span><span class="token punctuation">]</span><span class="token punctuation">)</span>
    q<span class="token punctuation">,</span> k<span class="token punctuation">,</span> v <span class="token operator">=</span> qkv<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span><span class="token punctuation">,</span> qkv<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">,</span> qkv<span class="token punctuation">[</span><span class="token number">2</span><span class="token punctuation">]</span>  <span class="token comment"># make torchscript happy (cannot use tensor as tuple)</span>

    q <span class="token operator">=</span> q <span class="token operator">*</span> self<span class="token punctuation">.</span>scale
    attn <span class="token operator">=</span> q @ swapdim<span class="token punctuation">(</span>k <span class="token punctuation">,</span><span class="token operator">-</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">)</span>

    relative_position_bias <span class="token operator">=</span> paddle<span class="token punctuation">.</span>index_select<span class="token punctuation">(</span>self<span class="token punctuation">.</span>relative_position_bias_table<span class="token punctuation">,</span>
                                                 self<span class="token punctuation">.</span>relative_position_index<span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">(</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">,</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">,</span>axis<span class="token operator">=</span><span class="token number">0</span><span class="token punctuation">)</span><span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">(</span>self<span class="token punctuation">.</span>window_size<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span> <span class="token operator">*</span> self<span class="token punctuation">.</span>window_size<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">,</span>self<span class="token punctuation">.</span>window_size<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span> <span class="token operator">*</span> self<span class="token punctuation">.</span>window_size<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">,</span> <span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">)</span><span class="token punctuation">)</span>

    relative_position_bias <span class="token operator">=</span> relative_position_bias<span class="token punctuation">.</span>transpose<span class="token punctuation">(</span><span class="token punctuation">[</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">)</span>  <span class="token comment"># nH, Wh*Ww, Wh*Ww</span>
    attn <span class="token operator">=</span> attn <span class="token operator">+</span> relative_position_bias<span class="token punctuation">.</span>unsqueeze<span class="token punctuation">(</span><span class="token number">0</span><span class="token punctuation">)</span>

    <span class="token keyword">if</span> mask <span class="token keyword">is</span> <span class="token keyword">not</span> <span class="token boolean">None</span><span class="token punctuation">:</span>
        nW <span class="token operator">=</span> mask<span class="token punctuation">.</span>shape<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span>
        attn <span class="token operator">=</span> attn<span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span>B_ <span class="token operator">//</span> nW<span class="token punctuation">,</span> nW<span class="token punctuation">,</span> self<span class="token punctuation">.</span>num_heads<span class="token punctuation">,</span> N<span class="token punctuation">,</span> N<span class="token punctuation">]</span><span class="token punctuation">)</span> <span class="token operator">+</span> mask<span class="token punctuation">.</span>unsqueeze<span class="token punctuation">(</span><span class="token number">1</span><span class="token punctuation">)</span><span class="token punctuation">.</span>unsqueeze<span class="token punctuation">(</span><span class="token number">0</span><span class="token punctuation">)</span>
        attn <span class="token operator">=</span> attn<span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">,</span> self<span class="token punctuation">.</span>num_heads<span class="token punctuation">,</span> N<span class="token punctuation">,</span> N<span class="token punctuation">]</span><span class="token punctuation">)</span>
        attn <span class="token operator">=</span> self<span class="token punctuation">.</span>softmax<span class="token punctuation">(</span>attn<span class="token punctuation">)</span>
    <span class="token keyword">else</span><span class="token punctuation">:</span>
        attn <span class="token operator">=</span> self<span class="token punctuation">.</span>softmax<span class="token punctuation">(</span>attn<span class="token punctuation">)</span>

    attn <span class="token operator">=</span> self<span class="token punctuation">.</span>attn_drop<span class="token punctuation">(</span>attn<span class="token punctuation">)</span>

    x <span class="token operator">=</span> swapdim<span class="token punctuation">(</span><span class="token punctuation">(</span>attn @ v<span class="token punctuation">)</span><span class="token punctuation">,</span><span class="token number">1</span><span class="token punctuation">,</span> <span class="token number">2</span><span class="token punctuation">)</span><span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">[</span>B_<span class="token punctuation">,</span> N<span class="token punctuation">,</span> C<span class="token punctuation">]</span><span class="token punctuation">)</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>proj<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>proj_drop<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token keyword">return</span> x

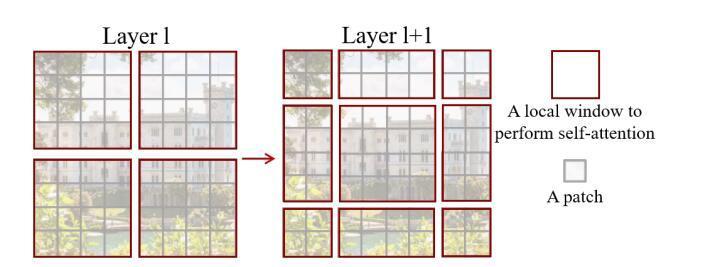
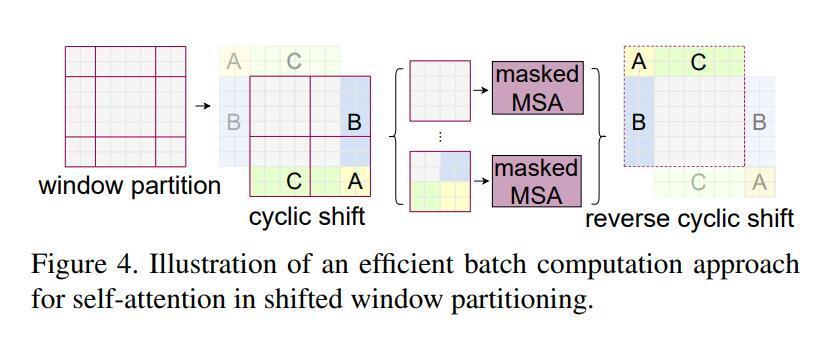
4.2 Swin Trasnformer模型实现

Swin Transformer涉及模型代码较多，所以建议完整的看Swin Transformer的代码，因此推荐一下桨的Swin Transformer实现。

4.3 Swin Trasnformer模型特点

首次在cv领域的transformer模型中采用了分层结构。分层结构因为其不同大小的尺度，使不同层特征有了更加不同的意义，较浅层的特征具有大尺度和细节信息，较深层的特征具有小尺度和物体的整体轮廓信息，在图像分类领域，深层特征具有更加有用的作用，只需要根据这个信息判定物体的类别即可，但是在像素级的分割和检测任务中，则需要更为精细的细节信息，因此，分层结构的模型往往更适用于分割和检测这样的像素级要求的任务中。Swin Transformer 模仿ResNet采取了分层的结构，使其成为了cv领域的通用框架。
引入locality思想，对无重合的window区域内进行self-attention计算。不仅减少了计算量，而且多了不同窗口之间的交互。

4.4 Swin Trasnformer模型效果

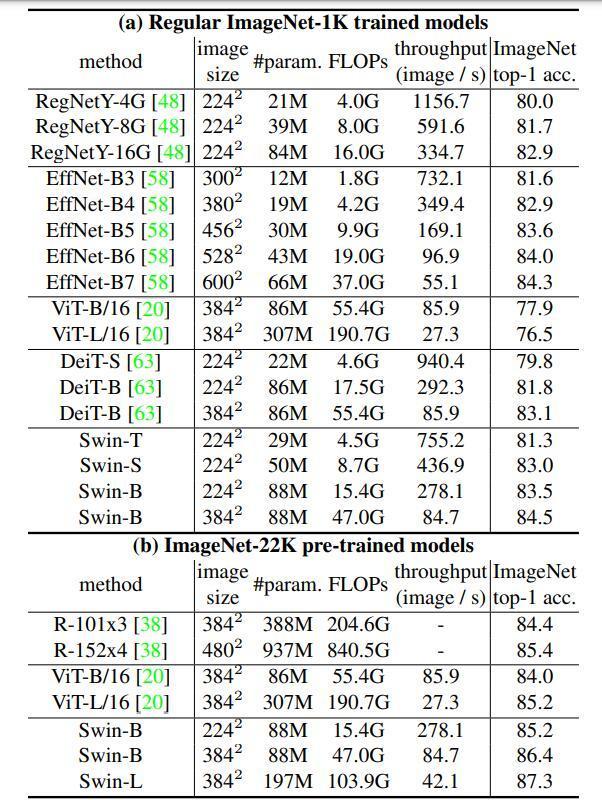
第一列为对比的方法，第二列为图片尺寸的大小（尺寸越大浮点运算量越大），第三列为参数量，第四列为浮点运算量，第五列为模型吞吐量。可以看出，Swin-T 在top1准确率上超过了大部分模型EffNet-B3确实是个优秀的网络，在参数量和FLOPs都比Swin-T少的情况下，略优于Swin-T,然而，基于ImageNet1K数据集，Swin-B在这些模型上取得了最优的效果。另外，Swin-L在ImageNet-22K上的top1准确率达到了87.3%的高度，这是以往的模型都没有达到的。并且Swin Transformer的其他配置也取得了优秀的成绩。图中不同配置的Swin Transformer解释如下。

C就是上面提到的类似于通道数的值，layer numbers就是Swin Transformer Block的数量了。这两个都是值越大，效果越好。和ResNet十分相似。

下图为COCO数据集上目标检测与实例分割的表现。都是相同网络在不同骨干网络下的对比。可以看出在不同AP下，Swin Transformer都有大约5%的提升，这已经是很优秀的水平了。怪不得能成为ICCV2021最佳paer。

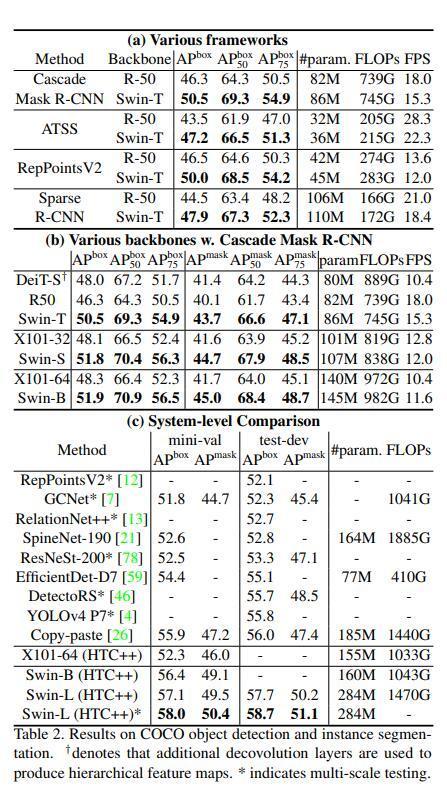
下图为语义分割数据集ADE20K上的表现。相较于同为transformer的DeiT-S, Swin Transformer-S有了5%的性能提升。相较于ResNeSt-200，Swin Transformer-L也有5%的提升。另外可以看到，在UNet的框架下，Swin Transformer的各个版本都有十分优秀的成绩，这充分说明了Swin Transformer是CV领域的通用骨干网络。

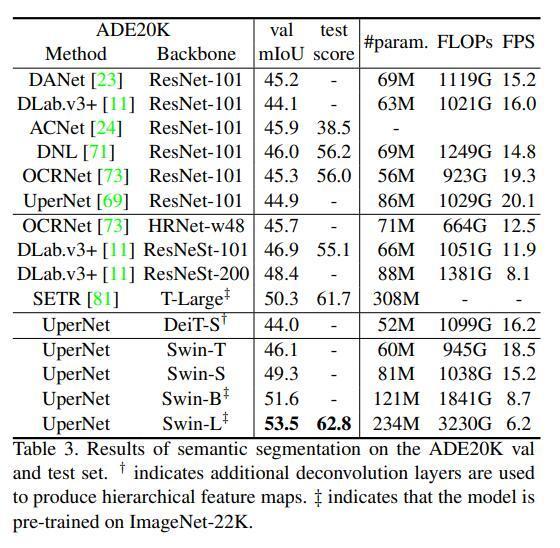
参考文献
Swin Transformer

5.ViT( Vision Transformer-2020)

在计算机视觉领域中，多数算法都是保持CNN整体结构不变，在CNN中增加attention模块或者使用attention模块替换CNN中的某些部分。有研究者提出，没有必要总是依赖于CNN。因此，作者提出ViT^[1]算法，仅仅使用Transformer结构也能够在图像分类任务中表现很好。

受到NLP领域中Transformer成功应用的启发，ViT算法中尝试将标准的Transformer结构直接应用于图像，并对整个图像分类流程进行最少的修改。具体来讲，ViT算法中，会将整幅图像拆分成小图像块，然后把这些小图像块的线性嵌入序列作为Transformer的输入送入网络，然后使用监督学习的方式进行图像分类的训练。

该算法在中等规模（例如ImageNet）以及大规模（例如ImageNet-21K、JFT-300M）数据集上进行了实验验证，发现：

Transformer相较于CNN结构，缺少一定的平移不变性和局部感知性，因此在数据量不充分时，很难达到同等的效果。具体表现为使用中等规模的ImageNet训练的Transformer会比ResNet在精度上低几个百分点。
当有大量的训练样本时，结果则会发生改变。使用大规模数据集进行预训练后，再使用迁移学习的方式应用到其他数据集上，可以达到或超越当前的SOTA水平。

5.1 ViT模型结构与实现

ViT算法的整体结构如图1 所示。

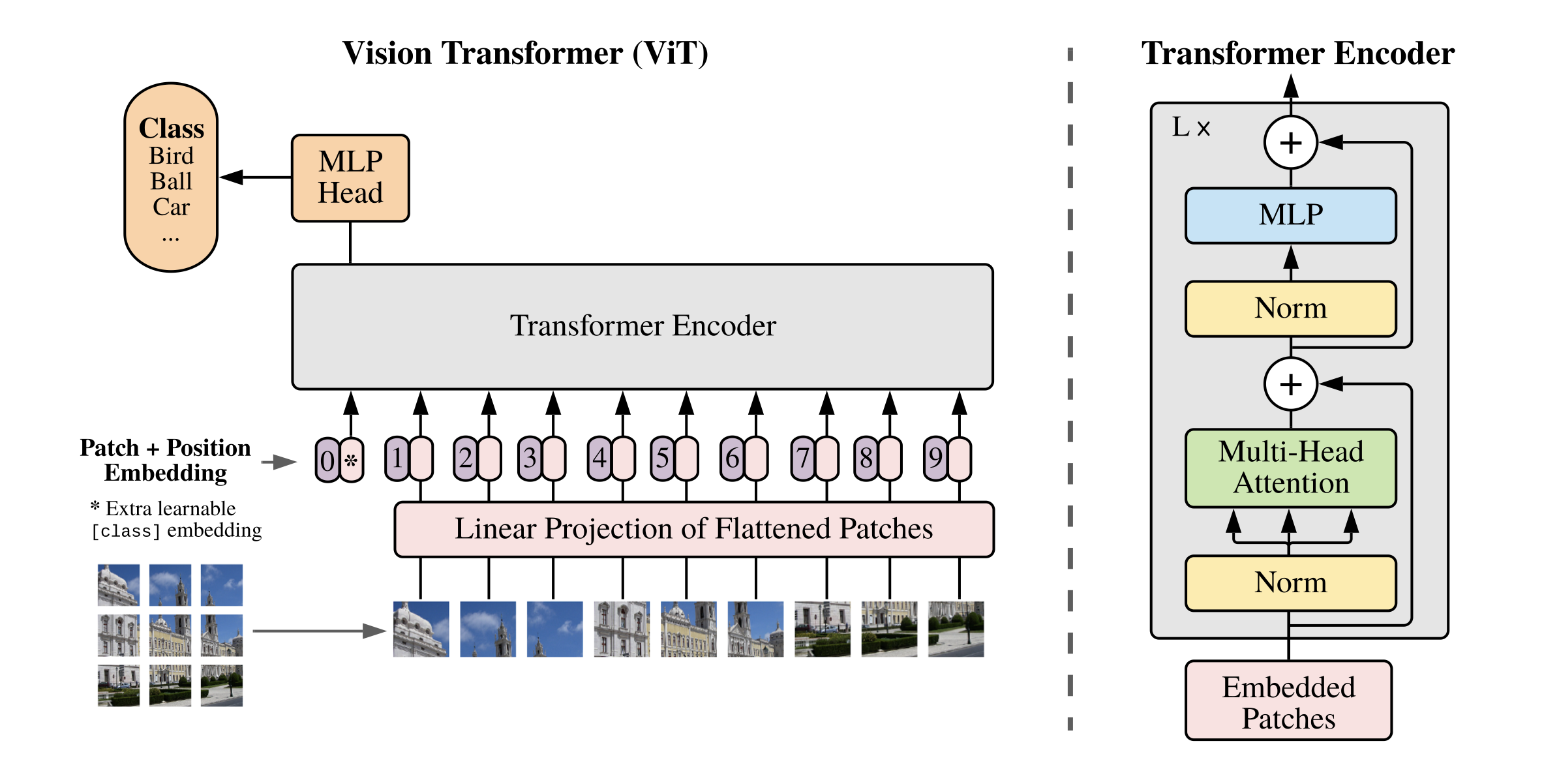
5.1.1. ViT图像分块嵌入

考虑到在Transformer结构中，输入是一个二维的矩阵，矩阵的形状可以表示为

     ( 
    
   
     N 
    
   
     , 
    
   
     D 
    
   
     ) 
    
   
  
    (N,D) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">D</span><span class="mclose">)</span></span></span></span></span>，其中 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     N 
    
   
  
    N 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span></span></span></span></span> 是sequence的长度，而 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     D 
    
   
  
    D 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">D</span></span></span></span></span> 是sequence中每个向量的维度。因此，在ViT算法中，首先需要设法将 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     H 
    
   
     × 
    
   
     W 
    
   
     × 
    
   
     C 
    
   
  
    H \times W \times C 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7667em; vertical-align: -0.0833em;"></span><span class="mord mathnormal" style="margin-right: 0.0813em;">H</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.7667em; vertical-align: -0.0833em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">W</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.0715em;">C</span></span></span></span></span> 的三维图像转化为 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     ( 
    
   
     N 
    
   
     , 
    
   
     D 
    
   
     ) 
    
   
  
    (N,D) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">D</span><span class="mclose">)</span></span></span></span></span> 的二维输入。</p>

ViT中的具体实现方式为：将

     H 
    
   
     × 
    
   
     W 
    
   
     × 
    
   
     C 
    
   
  
    H \times W \times C 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7667em; vertical-align: -0.0833em;"></span><span class="mord mathnormal" style="margin-right: 0.0813em;">H</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.7667em; vertical-align: -0.0833em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">W</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.0715em;">C</span></span></span></span></span> 的图像，变为一个 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     N 
    
   
     × 
    
   
     ( 
    
    
    
      P 
     
    
      2 
     
    
   
     ∗ 
    
   
     C 
    
   
     ) 
    
   
  
    N \times (P^2 * C) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7667em; vertical-align: -0.0833em;"></span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1.0641em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0715em;">C</span><span class="mclose">)</span></span></span></span></span> 的序列。这个序列可以看作是一系列展平的图像块，也就是将图像切分成小块后，再将其展平。该序列中一共包含了 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     N 
    
   
     = 
    
   
     H 
    
   
     W 
    
   
     / 
    
    
    
      P 
     
    
      2 
     
    
   
  
    N=HW/P^2 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1.0641em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0813em;">H</span><span class="mord mathnormal" style="margin-right: 0.1389em;">W</span><span class="mord">/</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span></span> 个图像块，每个图像块的维度则是 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     ( 
    
    
    
      P 
     
    
      2 
     
    
   
     ∗ 
    
   
     C 
    
   
     ) 
    
   
  
    (P^2*C) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0641em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0715em;">C</span><span class="mclose">)</span></span></span></span></span>。其中 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     P 
    
   
  
    P 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span></span></span></span></span> 是图像块的大小，<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     C 
    
   
  
    C 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.0715em;">C</span></span></span></span></span> 是通道数量。经过如上变换，就可以将 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     N 
    
   
  
    N 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span></span></span></span></span> 视为sequence的长度了。</p>

但是，此时每个图像块的维度是

     ( 
    
    
    
      P 
     
    
      2 
     
    
   
     ∗ 
    
   
     C 
    
   
     ) 
    
   
  
    (P^2*C) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0641em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0715em;">C</span><span class="mclose">)</span></span></span></span></span>，而我们实际需要的向量维度是 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     D 
    
   
  
    D 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">D</span></span></span></span></span>，因此我们还需要对图像块进行 Embedding。这里 Embedding 的方式非常简单，只需要对每个 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     ( 
    
    
    
      P 
     
    
      2 
     
    
   
     ∗ 
    
   
     C 
    
   
     ) 
    
   
  
    (P^2*C) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0641em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0715em;">C</span><span class="mclose">)</span></span></span></span></span> 的图像块做一个线性变换，将维度压缩为 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     D 
    
   
  
    D 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">D</span></span></span></span></span> 即可。</p>

上述对图像进行分块以及 Embedding 的具体方式如图2 所示。

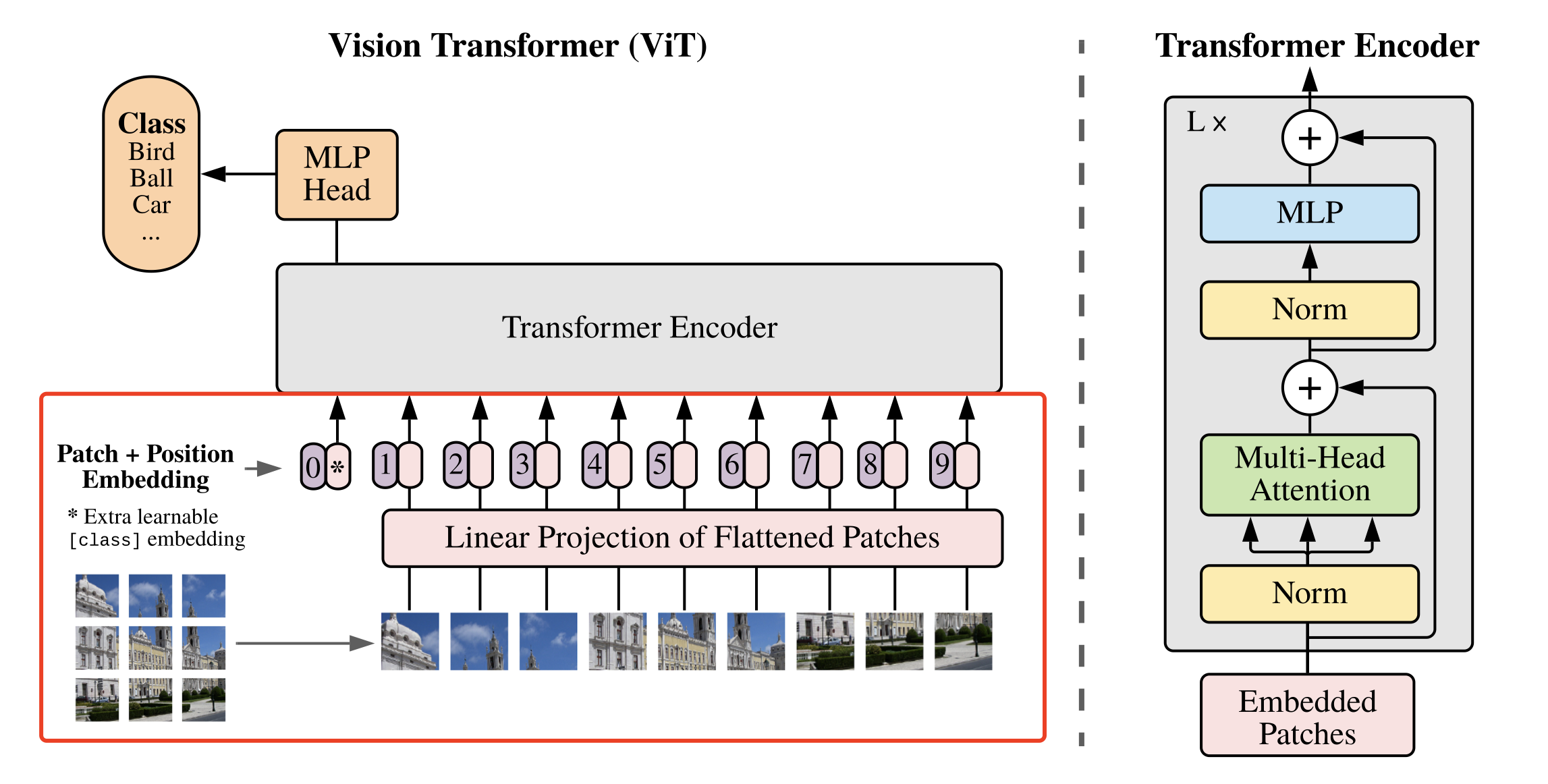
具体代码实现如下所示。本文中将每个大小为

     P 
    
   
  
    P 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span></span></span></span></span> 的图像块经过大小为 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     P 
    
   
  
    P 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span></span></span></span></span> 的卷积核来代替原文中将大小为 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     P 
    
   
  
    P 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6833em;"></span><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span></span></span></span></span> 的图像块展平后接全连接运算的操作。</p>

#图像分块、Embedding
class PatchEmbed(nn.Layer):
    def __init__(self, img_size=224, patch_size=16, in_chans=3, embed_dim=768):
        super().__init__()
        # 原始大小为int，转为tuple，即：img_size原始输入224，变换后为[224,224]
        img_size = to_2tuple(img_size)
        patch_size = to_2tuple(patch_size)
        # 图像块的个数
        num_patches = (img_size[1] // patch_size[1]) * \
            (img_size[0] // patch_size[0])
        self.img_size = img_size
        self.patch_size = patch_size
        self.num_patches = num_patches
        # kernel_size=块大小，即每个块输出一个值，类似每个块展平后使用相同的全连接层进行处理
        # 输入维度为3，输出维度为块向量长度
        # 与原文中：分块、展平、全连接降维保持一致
        # 输出为[B, C, H, W]
        self.proj = nn.Conv2D(
            in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)

    def forward(self, x):
        B, C, H, W = x.shape
        assert H == self.img_size[0] and W == self.img_size[1], \
            "Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."
        # [B, C, H, W] -> [B, C, H*W] ->[B, H*W, C]
        x = self.proj(x).flatten(2).transpose((0, 2, 1))
        return x

5.1.2. ViT多头注意力

将图像转化为

     N 
    
   
     × 
    
   
     ( 
    
    
    
      P 
     
    
      2 
     
    
   
     ∗ 
    
   
     C 
    
   
     ) 
    
   
  
    N \times (P^2 * C) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7667em; vertical-align: -0.0833em;"></span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1.0641em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.1389em;">P</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathnormal" style="margin-right: 0.0715em;">C</span><span class="mclose">)</span></span></span></span></span> 的序列后，就可以将其输入到 Transformer 结构中进行特征提取了，如 <strong>图3</strong> 所示。</p>

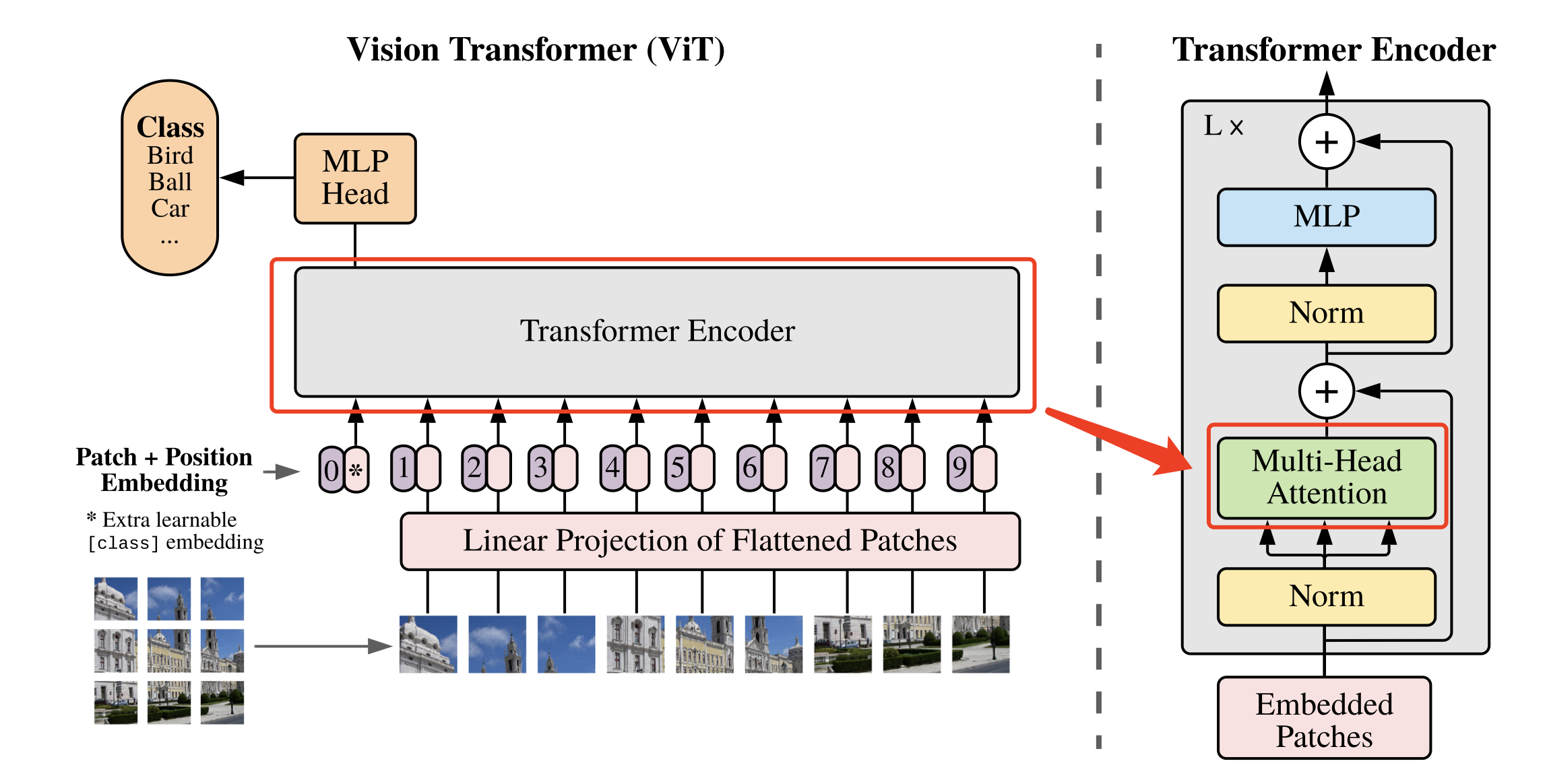
Transformer 结构中最重要的结构就是 Multi-head Attention，即多头注意力结构。具有2个head的 Multi-head Attention 结构如图4 所示。输入

      a 
     
    
      i 
     
    
   
  
    a^i 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.8247em;"></span><span class="mord"><span class="mord mathnormal">a</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8247em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span></span></span></span></span></span></span></span></span> 经过转移矩阵，并切分生成 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      q 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       1 
      
     
       ) 
      
     
    
   
  
    q^{(i,1)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0824em; vertical-align: -0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span>、<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      q 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       2 
      
     
       ) 
      
     
    
   
  
    q^{(i,2)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0824em; vertical-align: -0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span>、<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      k 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       1 
      
     
       ) 
      
     
    
   
  
    k^{(i,1)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span>、<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      k 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       2 
      
     
       ) 
      
     
    
   
  
    k^{(i,2)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span>、<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      v 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       1 
      
     
       ) 
      
     
    
   
  
    v^{(i,1)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span>、<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      v 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       2 
      
     
       ) 
      
     
    
   
  
    v^{(i,2)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span>，然后 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      q 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       1 
      
     
       ) 
      
     
    
   
  
    q^{(i,1)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0824em; vertical-align: -0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span> 与 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      k 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       1 
      
     
       ) 
      
     
    
   
  
    k^{(i,1)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span> 做 attention，得到权重向量 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     α 
    
   
  
    \alpha 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.0037em;">α</span></span></span></span></span>，将 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     α 
    
   
  
    \alpha 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.0037em;">α</span></span></span></span></span> 与 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      v 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       1 
      
     
       ) 
      
     
    
   
  
    v^{(i,1)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span> 进行加权求和，得到最终的 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      b 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       1 
      
     
       ) 
      
     
    
   
     ( 
    
   
     i 
    
   
     = 
    
   
     1 
    
   
     , 
    
   
     2 
    
   
     , 
    
   
     … 
    
   
     , 
    
   
     N 
    
   
     ) 
    
   
  
    b^{(i,1)}(i=1,2,…,N) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.138em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathnormal">i</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="minner">…</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span><span class="mclose">)</span></span></span></span></span>，同理可以得到 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      b 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       2 
      
     
       ) 
      
     
    
   
     ( 
    
   
     i 
    
   
     = 
    
   
     1 
    
   
     , 
    
   
     2 
    
   
     , 
    
   
     … 
    
   
     , 
    
   
     N 
    
   
     ) 
    
   
  
    b^{(i,2)}(i=1,2,…,N) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.138em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathnormal">i</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="minner">…</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span><span class="mclose">)</span></span></span></span></span>。接着将它们拼接起来，通过一个线性层进行处理，得到最终的结果。</p>

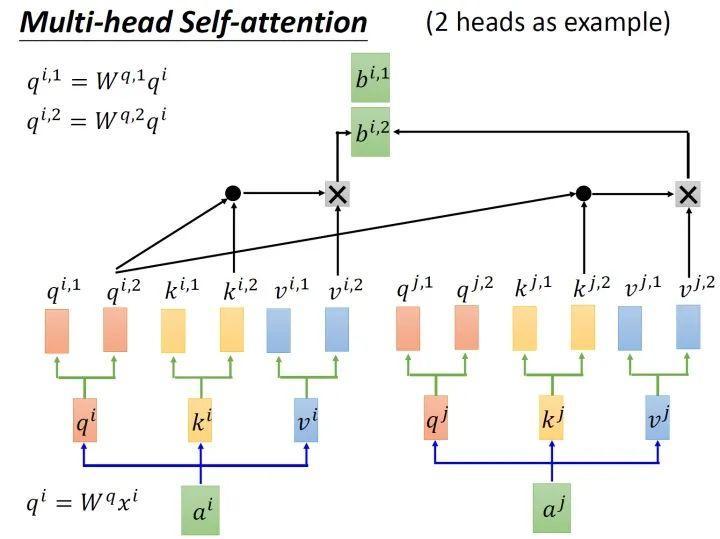
其中，使用

      q 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       j 
      
     
       ) 
      
     
    
   
  
    q^{(i,j)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0824em; vertical-align: -0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">j</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span>、<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      k 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       j 
      
     
       ) 
      
     
    
   
  
    k^{(i,j)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">j</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span> 与 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      v 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       j 
      
     
       ) 
      
     
    
   
  
    v^{(i,j)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">j</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span> 计算 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      b 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       j 
      
     
       ) 
      
     
    
   
     ( 
    
   
     i 
    
   
     = 
    
   
     1 
    
   
     , 
    
   
     2 
    
   
     , 
    
   
     … 
    
   
     , 
    
   
     N 
    
   
     ) 
    
   
  
    b^{(i,j)}(i=1,2,…,N) 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.138em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">j</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathnormal">i</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="minner">…</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.1667em;"></span><span class="mord mathnormal" style="margin-right: 0.109em;">N</span><span class="mclose">)</span></span></span></span></span> 的方法是缩放点积注意力 (Scaled Dot-Product Attention)。 结构如 <strong>图5</strong> 所示。首先使用每个 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      q 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       j 
      
     
       ) 
      
     
    
   
  
    q^{(i,j)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0824em; vertical-align: -0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">j</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span> 去与 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      k 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       j 
      
     
       ) 
      
     
    
   
  
    k^{(i,j)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">j</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span> 做 attention，这里说的 attention 就是匹配这两个向量有多接近，具体的方式就是计算向量的加权内积，得到 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      α 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       j 
      
     
       ) 
      
     
    
   
  
    \alpha_{(i,j)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7858em; vertical-align: -0.3552em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3448em;"><span class="" style="top: -2.5198em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">j</span><span class="mclose mtight">)</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.3552em;"><span class=""></span></span></span></span></span></span></span></span></span></span>。这里的加权内积计算方式如下所示：</p>

       α 
      
      
      
        ( 
       
      
        1 
       
      
        , 
       
      
        i 
       
      
        ) 
       
      
     
    
      = 
     
     
     
       q 
      
     
       1 
      
     
    
      ∗ 
     
     
     
       k 
      
     
       i 
      
     
    
      / 
     
     
     
       d 
      
     
    
   
     \alpha_{(1,i)} = q^1 * k^i / \sqrt{d} 
    
   
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7858em; vertical-align: -0.3552em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3448em;"><span class="" style="top: -2.5198em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight">i</span><span class="mclose mtight">)</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.3552em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1.0585em; vertical-align: -0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 1.2311em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8747em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">i</span></span></span></span></span></span></span></span><span class="mord">/</span><span class="mord sqrt"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.9811em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord" style="padding-left: 0.833em;"><span class="mord mathnormal">d</span></span></span><span class="" style="top: -2.9411em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail" style="min-width: 0.853em; height: 1.08em;"> 
        <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice"> 
         <path d="M95,702

c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14
c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54
c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10
s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429
c69,-144,104.5,-217.7,106.5,-221
l0 -0
c5.3,-9.3,12,-14,20,-14
H400000v40H845.2724
s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7
c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z
M834 80h400000v40h-400000z">

其中，

     d 
    
   
  
    d 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal">d</span></span></span></span></span> 是 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     q 
    
   
  
    q 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.1944em;"></span><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span></span></span></span></span> 和 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     k 
    
   
  
    k 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span></span></span></span></span> 的维度，因为 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
   
     q 
    
   
     ∗ 
    
   
     k 
    
   
  
    q*k 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6597em; vertical-align: -0.1944em;"></span><span class="mord mathnormal" style="margin-right: 0.0359em;">q</span><span class="mspace" style="margin-right: 0.2222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222em;"></span></span><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal" style="margin-right: 0.0315em;">k</span></span></span></span></span> 的数值会随着维度的增大而增大，因此除以 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      d 
     
    
   
  
    \sqrt{d} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.04em; vertical-align: -0.1078em;"></span><span class="mord sqrt"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.9322em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord" style="padding-left: 0.833em;"><span class="mord mathnormal">d</span></span></span><span class="" style="top: -2.8922em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail" style="min-width: 0.853em; height: 1.08em;"> 
       <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice"> 
        <path d="M95,702

接下来，把计算得到的

      α 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       j 
      
     
       ) 
      
     
    
   
  
    \alpha_{(i,j)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.7858em; vertical-align: -0.3552em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3448em;"><span class="" style="top: -2.5198em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">j</span><span class="mclose mtight">)</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.3552em;"><span class=""></span></span></span></span></span></span></span></span></span></span> 取 softmax 操作，再将其与 <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
 
  
   
    
    
      v 
     
     
     
       ( 
      
     
       i 
      
     
       , 
      
     
       j 
      
     
       ) 
      
     
    
   
  
    v^{(i,j)} 
   
  
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.888em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0359em;">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.888em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mopen mtight">(</span><span class="mord mathnormal mtight">i</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight" style="margin-right: 0.0572em;">j</span><span class="mclose mtight">)</span></span></span></span></span></span></span></span></span></span></span></span></span> 相乘。</p>

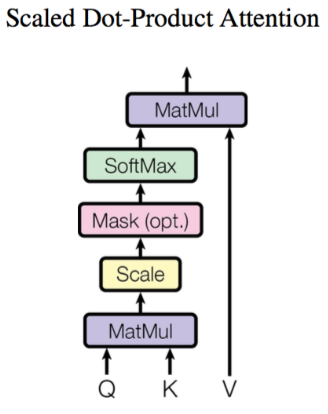
具体代码实现如下所示。

#Multi-head Attention
class Attention(nn.Layer):
    def __init__(self,
                 dim,
                 num_heads=8,
                 qkv_bias=False,
                 qk_scale=None,
                 attn_drop=0.,
                 proj_drop=0.):
        super().__init__()
        self.num_heads = num_heads
        head_dim = dim // num_heads
        self.scale = qk_scale or head_dim**-0.5
        # 计算 q,k,v 的转移矩阵
        self.qkv = nn.Linear(dim, dim * 3, bias_attr=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        # 最终的线性层
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)
<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> x<span class="token punctuation">)</span><span class="token punctuation">:</span>
    N<span class="token punctuation">,</span> C <span class="token operator">=</span> x<span class="token punctuation">.</span>shape<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">:</span><span class="token punctuation">]</span>
    <span class="token comment"># 线性变换</span>
    qkv <span class="token operator">=</span> self<span class="token punctuation">.</span>qkv<span class="token punctuation">(</span>x<span class="token punctuation">)</span><span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">(</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">,</span> N<span class="token punctuation">,</span> <span class="token number">3</span><span class="token punctuation">,</span> self<span class="token punctuation">.</span>num_heads<span class="token punctuation">,</span> C <span class="token operator">//</span>
                               self<span class="token punctuation">.</span>num_heads<span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">.</span>transpose<span class="token punctuation">(</span><span class="token punctuation">(</span><span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">0</span><span class="token punctuation">,</span> <span class="token number">3</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">,</span> <span class="token number">4</span><span class="token punctuation">)</span><span class="token punctuation">)</span>
    <span class="token comment"># 分割 query key value</span>
    q<span class="token punctuation">,</span> k<span class="token punctuation">,</span> v <span class="token operator">=</span> qkv<span class="token punctuation">[</span><span class="token number">0</span><span class="token punctuation">]</span><span class="token punctuation">,</span> qkv<span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">,</span> qkv<span class="token punctuation">[</span><span class="token number">2</span><span class="token punctuation">]</span>
    <span class="token comment"># Scaled Dot-Product Attention</span>
    <span class="token comment"># Matmul + Scale</span>
    attn <span class="token operator">=</span> <span class="token punctuation">(</span>q<span class="token punctuation">.</span>matmul<span class="token punctuation">(</span>k<span class="token punctuation">.</span>transpose<span class="token punctuation">(</span><span class="token punctuation">(</span><span class="token number">0</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">,</span> <span class="token number">3</span><span class="token punctuation">,</span> <span class="token number">2</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">)</span> <span class="token operator">*</span> self<span class="token punctuation">.</span>scale
    <span class="token comment"># SoftMax</span>
    attn <span class="token operator">=</span> nn<span class="token punctuation">.</span>functional<span class="token punctuation">.</span>softmax<span class="token punctuation">(</span>attn<span class="token punctuation">,</span> axis<span class="token operator">=</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">)</span>
    attn <span class="token operator">=</span> self<span class="token punctuation">.</span>attn_drop<span class="token punctuation">(</span>attn<span class="token punctuation">)</span>
    <span class="token comment"># Matmul</span>
    x <span class="token operator">=</span> <span class="token punctuation">(</span>attn<span class="token punctuation">.</span>matmul<span class="token punctuation">(</span>v<span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">.</span>transpose<span class="token punctuation">(</span><span class="token punctuation">(</span><span class="token number">0</span><span class="token punctuation">,</span> <span class="token number">2</span><span class="token punctuation">,</span> <span class="token number">1</span><span class="token punctuation">,</span> <span class="token number">3</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">.</span>reshape<span class="token punctuation">(</span><span class="token punctuation">(</span><span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">,</span> N<span class="token punctuation">,</span> C<span class="token punctuation">)</span><span class="token punctuation">)</span>
    <span class="token comment"># 线性变换</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>proj<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>proj_drop<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token keyword">return</span> x

5.1.3. 多层感知机（MLP）

Transformer 结构中还有一个重要的结构就是 MLP，即多层感知机，如图6 所示。

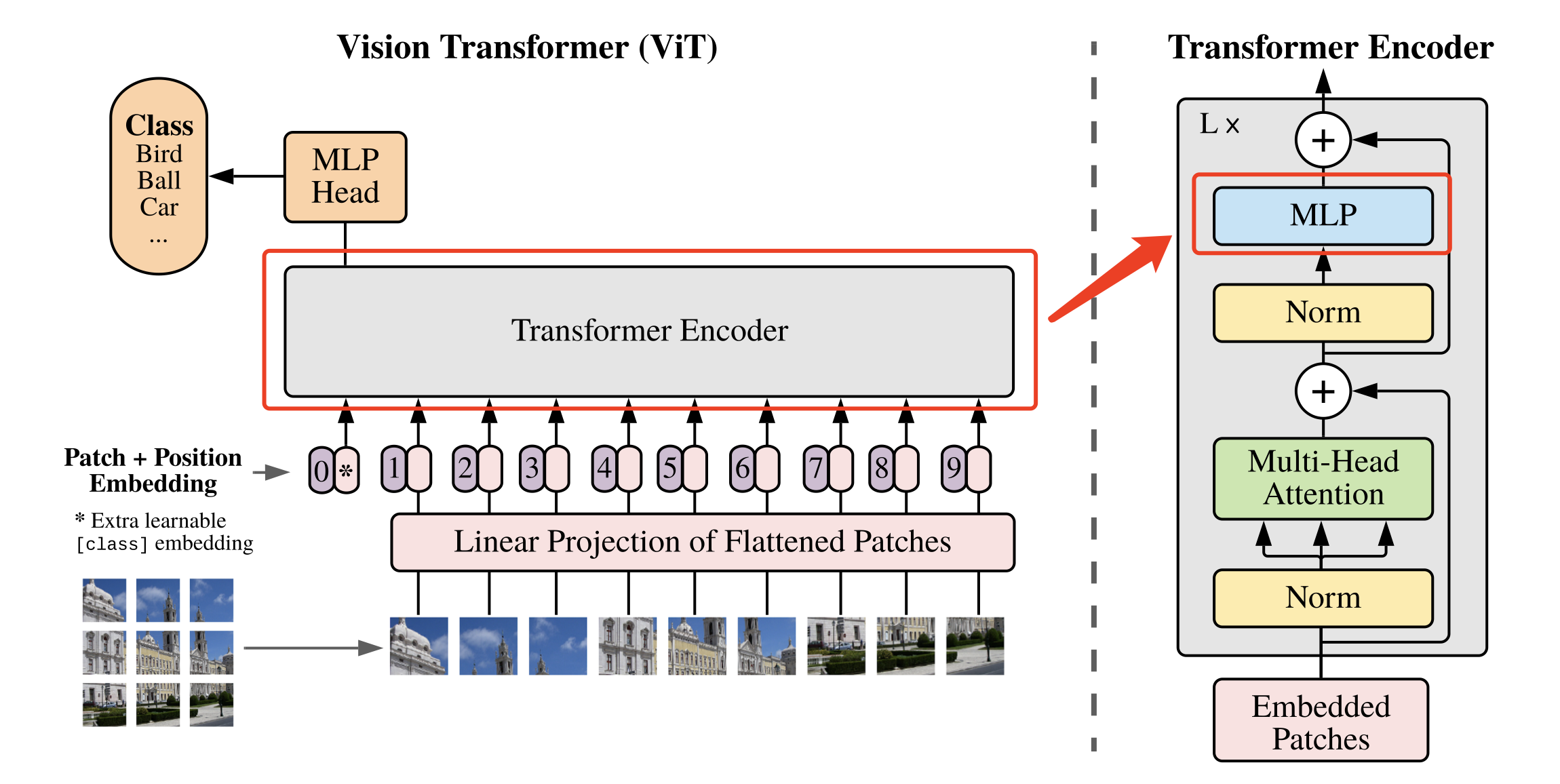
多层感知机由输入层、输出层和至少一层的隐藏层构成。网络中各个隐藏层中神经元可接收相邻前序隐藏层中所有神经元传递而来的信息，经过加工处理后将信息输出给相邻后续隐藏层中所有神经元。在多层感知机中，相邻层所包含的神经元之间通常使用“全连接”方式进行连接。多层感知机可以模拟复杂非线性函数功能，所模拟函数的复杂性取决于网络隐藏层数目和各层中神经元数目。多层感知机的结构如图7 所示。

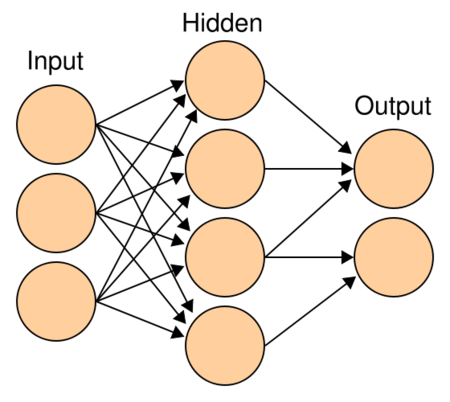
具体代码实现如下所示。

class Mlp(nn.Layer):
    def __init__(self,
                 in_features,
                 hidden_features=None,
                 out_features=None,
                 act_layer=nn.GELU,
                 drop=0.):
        super().__init__()
        out_features = out_features or in_features
        hidden_features = hidden_features or in_features
        self.fc1 = nn.Linear(in_features, hidden_features)
        self.act = act_layer()
        self.fc2 = nn.Linear(hidden_features, out_features)
        self.drop = nn.Dropout(drop)
<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> x<span class="token punctuation">)</span><span class="token punctuation">:</span>
    <span class="token comment"># 输入层：线性变换</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>fc1<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token comment"># 应用激活函数</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>act<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token comment"># Dropout</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>drop<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token comment"># 输出层：线性变换</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>fc2<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token comment"># Dropout</span>
    x <span class="token operator">=</span> self<span class="token punctuation">.</span>drop<span class="token punctuation">(</span>x<span class="token punctuation">)</span>
    <span class="token keyword">return</span> x

5.1.4. DropPath

除了以上重要模块意外，代码实现过程中还使用了DropPath（Stochastic Depth）来代替传统的Dropout结构，DropPath可以理解为一种特殊的 Dropout。其作用是在训练过程中随机丢弃子图层（randomly drop a subset of layers），而在预测时正常使用完整的 Graph。

具体实现如下：

def drop_path(x, drop_prob=0., training=False):
    if drop_prob == 0. or not training:
        return x
    keep_prob = paddle.to_tensor(1 - drop_prob)
    shape = (paddle.shape(x)[0], ) + (1, ) * (x.ndim - 1)
    random_tensor = keep_prob + paddle.rand(shape, dtype=x.dtype)
    random_tensor = paddle.floor(random_tensor)
    output = x.divide(keep_prob) * random_tensor
    return output

class DropPath(nn.Layer):
def init(self, drop_prob=None):
super(DropPath, self).init()
self.drop_prob = drop_prob

<span class="token keyword">def</span> <span class="token function">forward</span><span class="token punctuation">(</span>self<span class="token punctuation">,</span> x<span class="token punctuation">)</span><span class="token punctuation">:</span>
    <span class="token keyword">return</span> drop_path<span class="token punctuation">(</span>x<span class="token punctuation">,</span> self<span class="token punctuation">.</span>drop_prob<span class="token punctuation">,</span> self<span class="token punctuation">.</span>training<sp