吃瓜教程 —— 第三章

三. 线性模型

1. 基本形式

给定由d个属性描述的示例 x = (x_1;x_2;…;x_d)，其中x_i在第i个属性上的取值，线性模型表示为

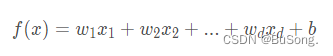
一般情况下用向量的形式，则表示成

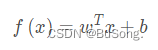
只要能够确定出 w 和 b 的值就可以确定这个线性模型了

2. 线性回归

线性回归是什么？
线性回归是通过学习一个线性模型，来预测出其对应的连续值，通过对预测值和真实值之间，尽可能缩小其欧氏距离，即使得 f (x_i ) ≈ y_i

2.1 最小二乘法

使用均方误差最小化来进行模型求解的，形如

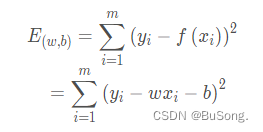
2.2 极大似然估计

假设线性回归模型如下所示，

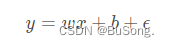
其中 ϵ 符合

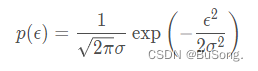
然后将 ϵ 用 y-(wx+b) 进行代替后，得到的式子为

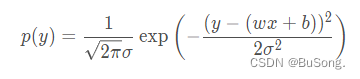
代入极大似然估计后，得到如下所示，

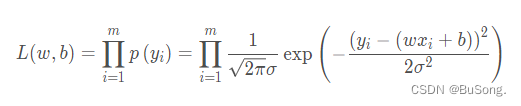
由于极大似然函数不好求，因此对上述的式子进行取对数，最终得出

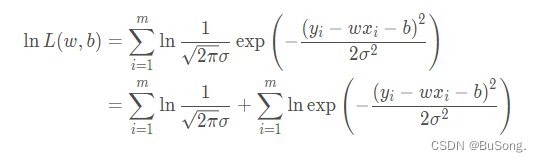
其中使用了 ln(ab)=lna+lnb 的性质

2.3 求解 w 和 b 的值

加上 argmin 后就变成

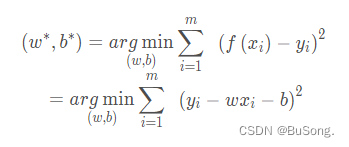
其中 argmin 表示当这个式子取最小的时候，w 和 b的取值是多少

由于上述的式子中存在着两个参数一个是 w ，一个是 b，因此对上述的式子，根据数分的知识，要求出其值，则分别对两个参数求偏导，令导数为0，即可求出连个参数的值
最终得出
w 的求解公式为

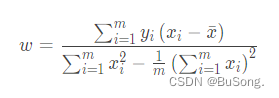
b 的求解公式是

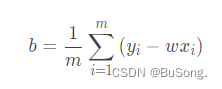
2.4 Hessian矩阵

用于判断这个函数是否为一个凸函数的办法，Hessian矩阵形如下所示，

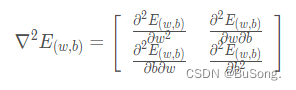
Hessian矩阵是针对于一个函数对其求二阶偏导，得出的一个矩阵，当这个矩阵为半正定的时候便可以说明这个函数为凸函数

2.5 多元线性回归

从一般的线性回归模型，到映射在n维空间上的多元线性回归，可以通过矩阵的形式表示出来，即

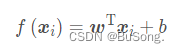
其中 w = (w_1,w_2,…w_n), x = (x_ 1,x _2 ,…x _n)，当然从满足矩阵运算的角度来说，对哪一个进行转置都是可以的，只不过是满足一列乘以一行的规律
根据均方差误差最小化原则有

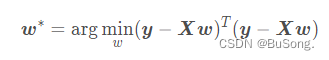
对 w 进行求导

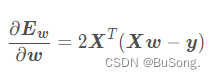
令导数为0，就可以求出来 w 的解

3. 对数几率回归

对数几率回归，又叫做逻辑回归，比如说将二分类的问题的结果转化为0-1上的值的输出，而最理想的单位阶跃函数是


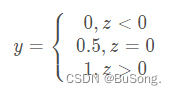
针对于上述的图，有一个函数可以代替图，其便是 sigmoid 函数

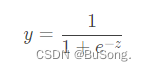
将线性模型 y=w^T_x+b 带入 sigmoid 函数中, 可以得到

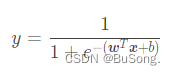
取对数后得到的操作如下所示

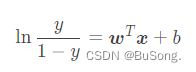
采用极大似然去求解，将模型改写如下

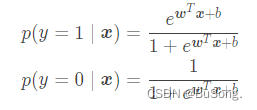
得到极大似然函数，并对极大似然函数进行求对数

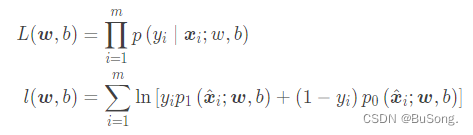
4. 线性判别分析(LDA)

LDA 的思想很朴素，通过给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离.

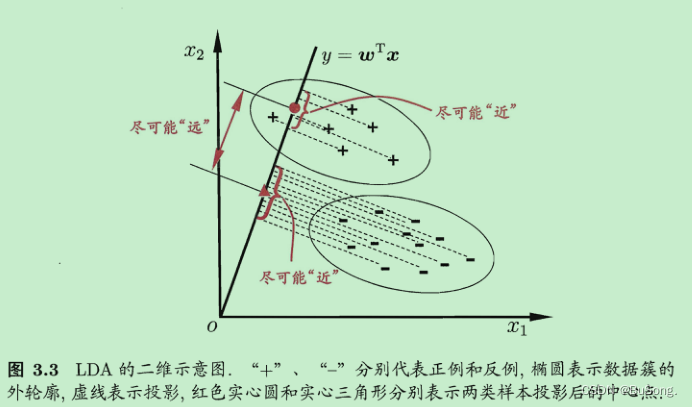
其中正例的投影为 w^Tu_0 ,
其协方差为 w^TΣ_0w,
负例的投影为 w ^Tu_1,
协方差为 w^TΣ_1w
使得同类样例的投影点尽可能接近，则可以让下面的等式尽可能小

使得异类样例的投影点尽可能远离，则可以让下面的等式尽可能大

二范式，就是通常意义上的模。
传送门：范式理解

因此得到一个目标函数 J

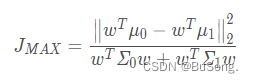
定义类内散度矩阵

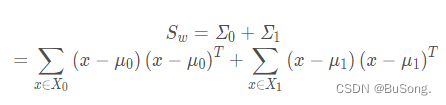
以及类间散度矩阵


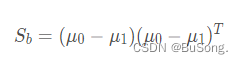
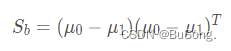
所以目标函数 J 可以改写成

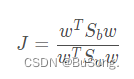
• 如何确定 W ？
  拉格朗日乘子法
  传送门：优化-拉格朗日乘子法

5. 多分类学习

• 一对一(OvO)
  假如某个分类中有N个类别，我们将这N个类别进行两两配对（两两配对后转化为二分类问题）。那么我们可以得到个二分类器。（简单解释一下，相当于在N个类别里面抽2个）
  之后，在测试阶段，我们把新样本交给这个二分类器。于是我们可以得到个分类结果。把预测的最多的类别作为预测的结果。
• 一对多(OvR)
  一对其余其实更加好理解，每次将一个类别作为正类，其余类别作为负类。此时共有（N个分类器）。在测试的时候若仅有一个分类器预测为正类，则对应的类别标记为最终的分类结果。
• 多对多(MvM)

传送门：多分类学习

6. 类别不平衡问题

当数据集中，正例和负例的不多的时候，需要对其进行重新采样，再缩放思想
解决类别不平衡的三类做法

1. 直接对训练集里的反类样例进行"欠采样"，即去除一些反例使得正反例数目接近
2. 对训练集里的正类样例进行"过采样"，即增加一些正例使得正反例数目接近，然后再学习
3. 直接基于原始训练集进行学习，但在用训练好的分类器进行预测时，称为"阈值移动"