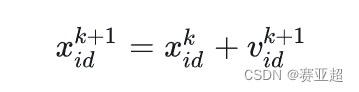粒子群优化pso结合bp神经网络优化对csv文件预测matlab(3)
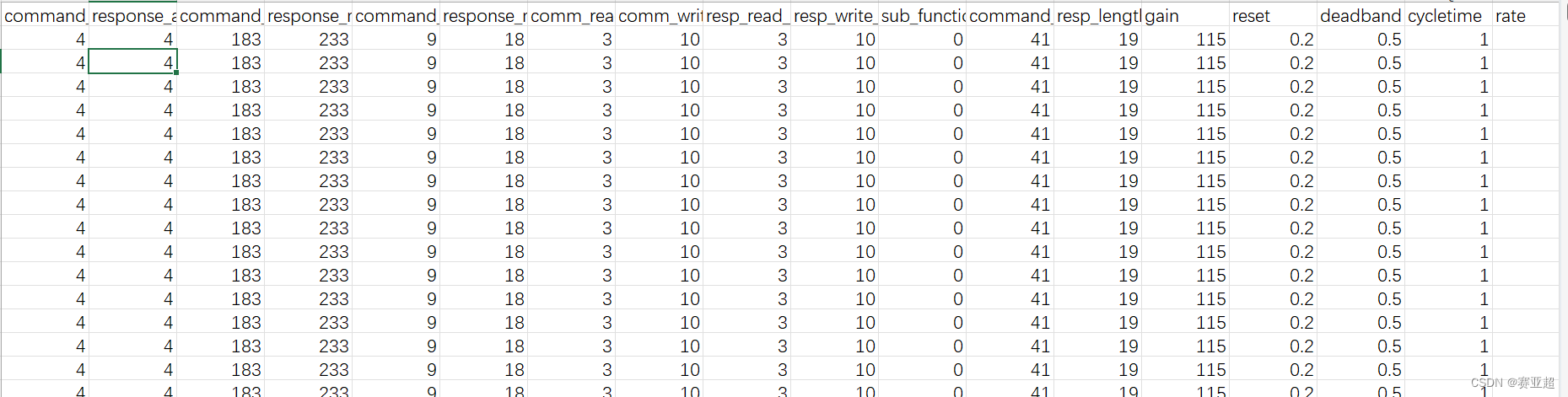
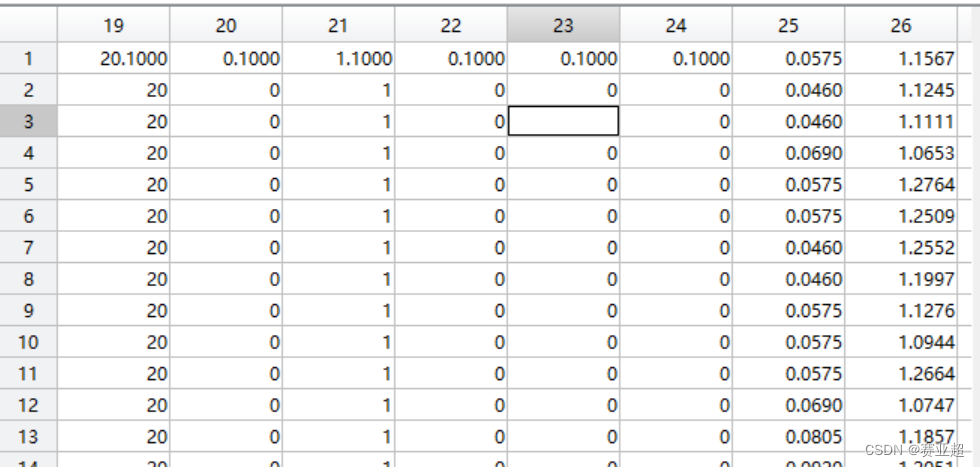
1.csv数据为密西西比数据集,获取数据集可以管我要,数据集内容形式如下图:
2.代码
这里参考的是b站的一位博主。
数据集导入教程在我的另一篇文章bp写过,需要的话可以去看一下
psobp.m
close all
clc
%读取数据
input=X;
output=Y;%10000行1列
%设置训练数据与测试数据
input_train=input(1:8000,:)';
output_train=output(1:8000,:)';
input_test=input(8001:10000,:)';
output_test=output(8001:10000,:)';%2000列1行
%节点个数
inputnum=26;%输入层节点数量
hiddennum=12;%隐藏层节点数量
outputnum=1;%输出层节点数量
w1num=inputnum*hiddennum;%输入层到隐藏层的权值个数
w2num=outputnum*hiddennum;%输出层到隐藏层的权值个数
N=w1num+hiddennum+w2num+outputnum;%待优化的变量个数
%训练数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
%%定义pso算法参数
E0=0.001;%允许误差
MaxNum=10;%粒子最大迭代次数
narvs=N;%目标函数的子变量个数
particlesize=10;%粒子群规模
c1=2;%个体经验学习因子
c2=2;%社会经验学习因子
w=0.6;%惯性因子
vmax=0.8;%粒子最大飞行速度
x=-5+10*rand(particlesize,narvs);%粒子所在位置,规模是粒子群数和参数需求数设置x的取值范围[-5,5]
v=2*rand(particlesize,narvs);%粒子飞行速度,生成每个粒子飞行速度,只有一个变量,所以速度是一维的
trace=zeros(N+1,MaxNum);%寻优结果的初始值
objv=objfun(x,input_train,output_train,input_test,output_test);%计算目标函数值
personalbest_x=x;%用于存储个体最优,存储每个粒子经历的x值
personalbest_faval=objv;%存储个体最优的y,每个个体的误差的群体
[globalbest_faval,i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:);%全局最优的x
k=1;%开始迭代
while k<=MaxNum
objv=objfun(x,input_train,output_train,input_test,output_test);
for i=1:particlesize
if objv(i)<personalbest_faval(i)
personalbest_faval(i)=objv(i);%将第i个粒子作为个体最优解
personalbest_x(i,:)=x(i,:);%更新最优解位置
end
end
[globalbest_favalN,i]=min(personalbest_faval);
globalbest_xn=personalbest_x(i,:);
trace(1:N,k)=globalbest_xn;%每代最优x值
trace(end,k)=globalbest_favalN;
%%粒子更新
for i=1:particlesize
v(i,:)=w*v(i,:)+c1*rand*(personalbest_x(i,:)-x(i,:))+c2*rand*(globalbest_x-x(i,:));
%rand会随机生成一个(0,1)的随机降低学习因子的比例
for j=1:narvs%确定每个变量的速度,不超过最大速度
if v(i,j)>vmax
v(i,j)=vmax;
elseif v(i,j)<-vmax
v(i,j)=-vmax;
end
end
x(i,:)=x(i,:)+v(i,:);
end
globalbest_faval=globalbest_favalN;
globalbest_x=globalbest_xn;
k=k+1;
end
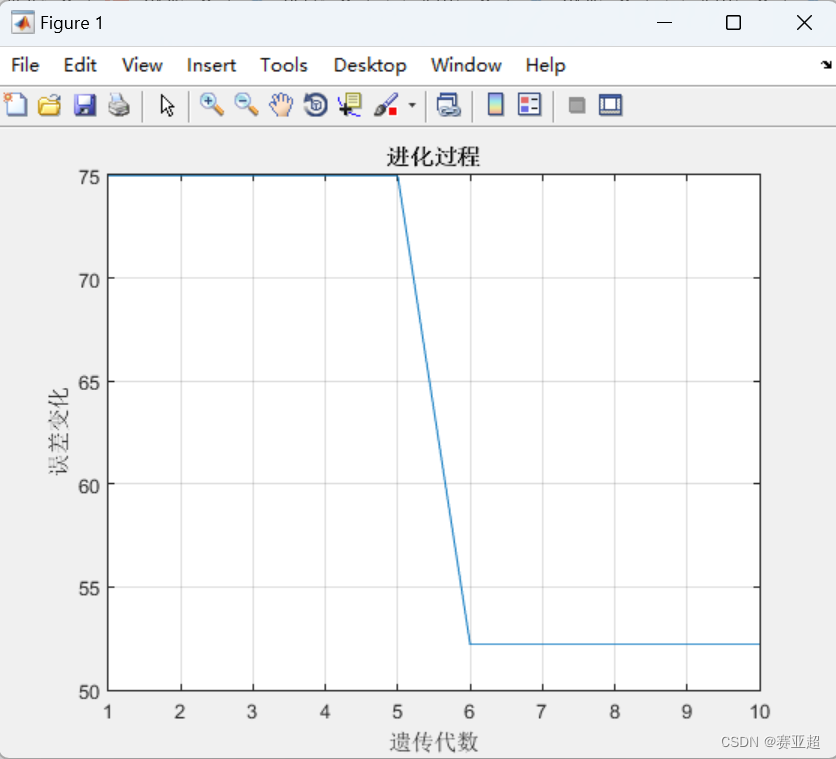
%%画图
figure(1);
plot(1:MaxNum,trace(end,:));
grid on;
xlabel('遗传代数');
ylabel('误差变化');
title('进化过程');
objfun.m
function [obj,T_sim]=objfun(X,input_train,output_train,input_test,output_test)
%%分别求解种群每个个体的目标值
%输入
%x:所有个体的初始权值与阈值
%input_train:训练样本输入
%output_train:训练样本输出
%hiddennum:隐藏神经元个数
%input_test:测试样本输入
%output_test:测试样本输出
%%输出
%obj:所有个体的预测样本的预测误差的范数,让这个误差最小,也就是每一个种群全都累加变成一个数,这里有10个种群,就是10个数
[M,N]=size(X);%返回一个M行N列的矩阵
obj=zeros(M,1);%所有个体误差初始化为M行1列也就是前面的粒子群规模,就是10行1列
T_sim=zeros(M,2000);%size(output_test,2)返回output_test的列数也就是2000个结果,也就是预测值是10行2000列的数值
for i=1:M
[obj(i),T_sim(i,:)]=BpFunction(X(i,:),input_train,output_train,input_test,output_test);
end
T_sim=T_sim';
endBpFunction.m
%%输入
function [err,T_sim]=BpFunction(x,input_train,output_train,input_test,output_test)
inputnum=26;%输入层节点数量
hiddennum=12;%隐藏层节点数量
outputnum=1;%输出层节点数量
%%数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);
[outputn,outputps]=mapminmax(output_train,0,1);
%bp神经网络
net=newff(inputn,outputn,hiddennum);
%网络参数配置
net.trainParam.epochs=30;
net.trainParam.lr=0.001;
net.trainParam.goal=0.0001;
w1num=inputnum*hiddennum;%输入层到隐藏层的权值个数
w2num=outputnum*hiddennum;%输出层到隐藏层的权值个数
W1=x(1:w1num);
B1=x(w1num+1:w1num+hiddennum);
W2=x(w1num+hiddennum+1:w1num+hiddennum+w2num);
B2=x(w1num+hiddennum+w2num+1:w1num+hiddennum+w2num+outputnum);
net.iw{1,1}=reshape(W1,hiddennum,inputnum);
net.lw{2,1}=reshape(W2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=reshape(B2,outputnum,1);
%%开始训练
%网络训练
net=train(net,inputn,outputn);
%%测试网络
t_sim=sim(net,input_test);
T_sim=mapminmax('reverse',t_sim,outputps);
err=norm(T_sim-output_test);
end3.结果
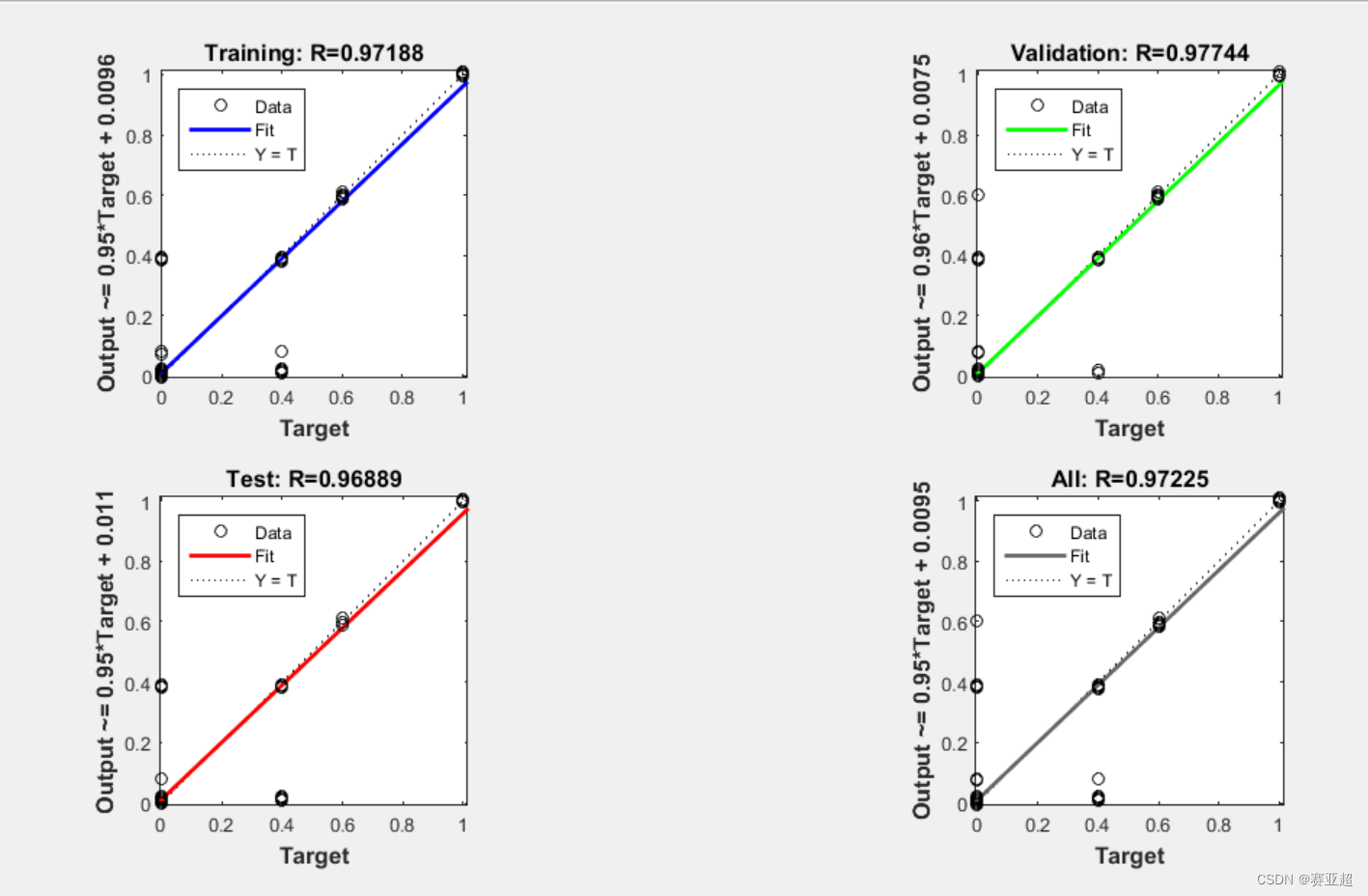
4.优化之前
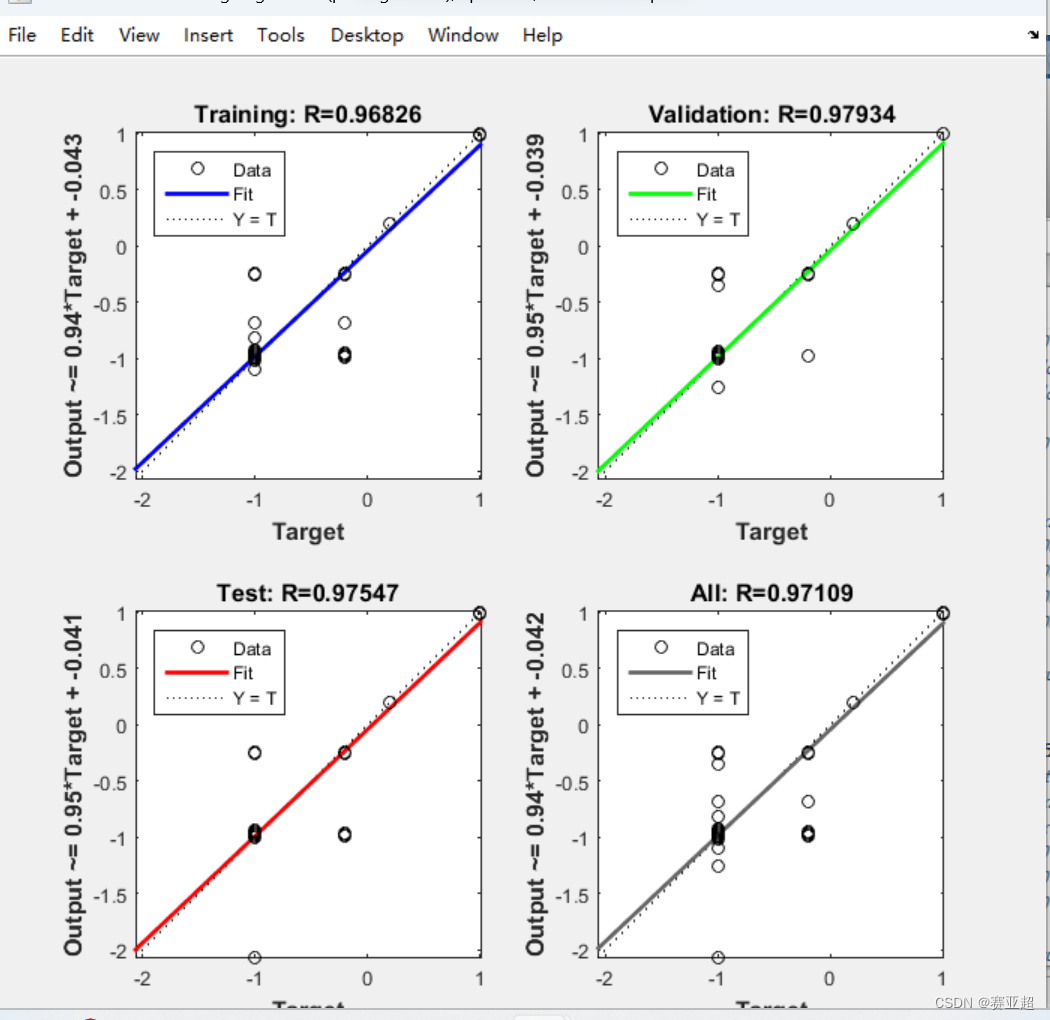
5.之所以上面有拟合差别大的地方在于bp网络自动将数据集中某一列全是一个数的给消去了,不知是系统消去的还是神经网络给消掉的。所以他会报错:
net.IW{1,1} must be a 12-by-8 matrix.
报这个错误的解决办法我是将某一列中第一行数据加个0.1。虽然是个解决办法,但是会影响到识别精度。所以不是个好办法。
1.1粒子群算法基础
Pso算法是从随机解出发,通过迭代寻找最优解,通过适应度来评价解的品质,但是它比遗传算法规则更为简单,它没有遗传算法的“交叉”和“变异”操作,它是通过追随当前搜索到的最优值来寻找全局最优。
1.2基本原理
Pso算法起源对简单社会的模拟,具有很好的生物社会背景。Pso中每个优化问题的潜在解都是搜索空间的一只鸟,称之为粒子。所有的粒子都有一个由被优化的函数决定的适应值,每个粒子还有一个速度决定他们”飞行“的方向和距离。然后粒子就追随当前的最优粒子在解空间中搜索。设想这样一个场景:鸟群在森林中随机搜索食物,它们想要找到食物量最多的位置。但是所有的鸟都不知道食物具体在哪个位置,只能感受到食物大概在哪个方向。每只鸟沿着自己判定的方向进行搜索,并在搜索的过程中记录自己曾经找到过食物且量最多的位置,同时所有的鸟都共享自己每一次发现食物的位置以及食物的量,这样鸟群就知道当前在哪个位置食物的量最多。在搜索的过程中每只鸟都会根据自己记忆中食物量最多的位置和当前鸟群记录的食物量最多的位置调整自己接下来搜索的方向。鸟群经过一段时间的搜索后就可以找到森林中哪个位置的食物量最多(全局最优解)。
(1)PSO的基础:信息的社会共享
(2)粒子的两个属性:速度和位置(算法的两个核心要素)
速度表示粒子下一步迭代时移动的方向和距离,位置是所求解问题的一个解。
算法的6个重要参数
假设在D维搜索空间中,有N个粒子,每个粒子代表一个解,则:
① 第i个粒子的位置为:
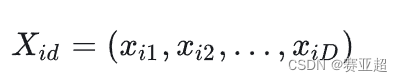
② 第 i个粒子的速度(粒子移动的距离和方向)为:
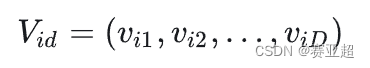
③ 第 i个粒子搜索到的最优位置(个体最优解)为:
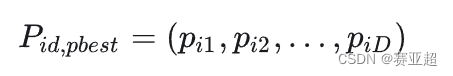
④ 群体搜索到的最优位置(群体最优解)为:
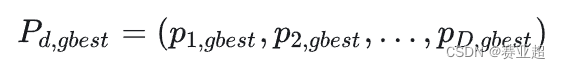
⑤ 第 i个粒子搜索到的最优位置的适应值(优化目标函数的值)为:
![]() ——个体历史最优适应值
——个体历史最优适应值
⑥ 群体搜索到的最优位置的适应值为:
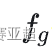 ——群体历史最优适应值
——群体历史最优适应值
1.3粒子群算法的流程图
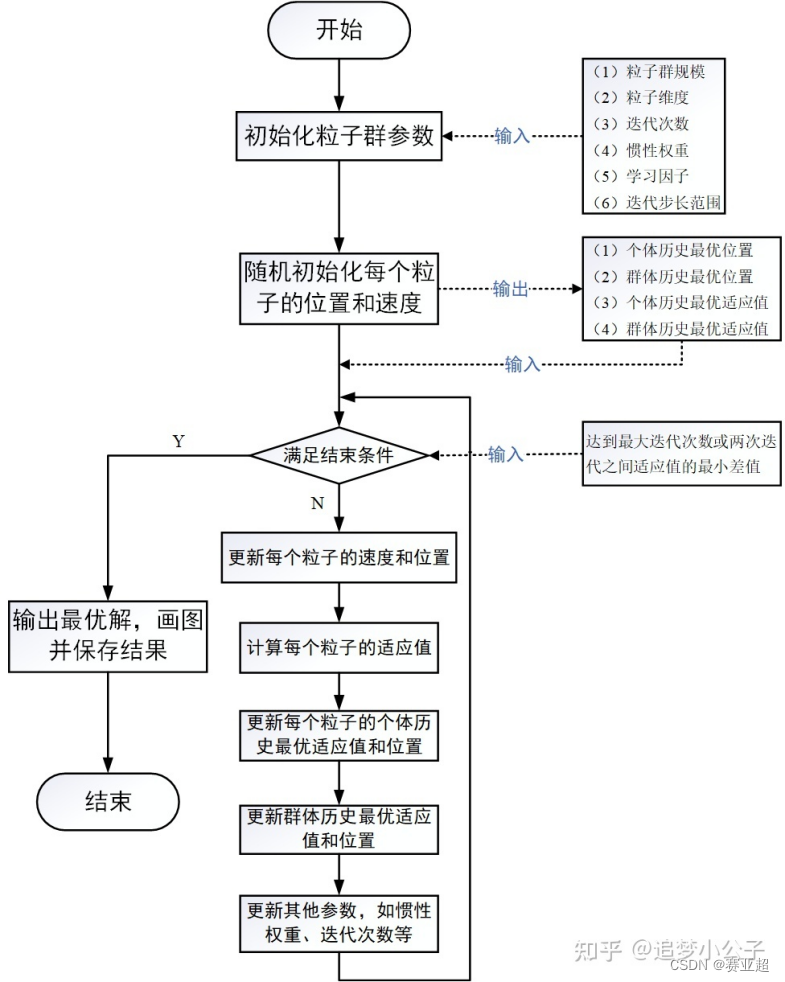
1.4粒子群算法的伪代码

1.5速度更新公式
表述上叫速度,实际上就是粒子下一步迭代移动的距离和方向,也就是一个位置向量。
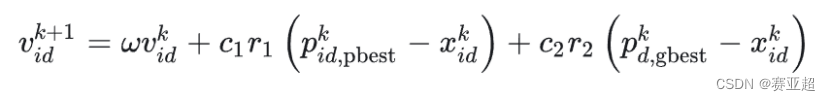
(1)速度更新公式的解释
① 第一项:惯性部分
由惯性权重和粒子自身速度构成,表示粒子对先前自身运动状态的信任。
② 第二项:认知部分
表示粒子本身的思考,即粒子自己经验的部分,可理解为粒子当前位置与自身历史最优位置之间的距离和方向。
③ 第三项:社会部分
表示粒子之间的信息共享与合作,即来源于群体中其他优秀粒子的经验,可理解为粒子当前位置与群体历史最优位置之间的距离和方向。
(2)速度更新公式的参数定义

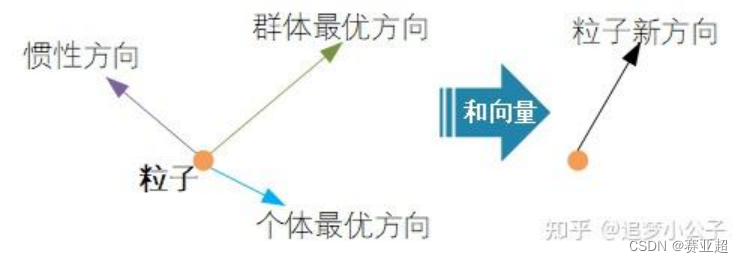
(3)速度的方向
粒子下一步迭代的移动方向 = 惯性方向 + 个体最优方向 + 群体最优方向
1.6、位置更新公式
上一步的位置 + 下一步的速度
1.7算法参数的详细解释
-
粒子群规模: N
一个正整数,推荐取值范围:[20,1000],简单问题一般取20~40,较难或特定类别的问题可以取100~200。较小的种群规模容易陷入局部最优;较大的种群规模可以提高收敛性,更快找到全局最优解,但是相应地每次迭代的计算量也会增大;当种群规模增大至一定水平时,再增大将不再有显著的作用。
(2)粒子维度: D
粒子搜索的空间维数即为自变量的个数。
(3)迭代次数: K
推荐取值范围:[50,100],典型取值:60、70、100;这需要在优化的过程中根据实际情况进行调整,迭代次数太小的话解不稳定,太大的话非常耗时,没有必要。
(4)惯性权重:w
1998年,Yuhui Shi和Russell Eberhart对基本粒子群算法引入了惯性权重(inertia weight)w,并提出动态调整惯性权重以平衡收敛的全局性和收敛速度,该算法被称为标准PSO算法。
参数意义
惯性权重w表示上一代粒子的速度对当代粒子的速度的影响,或者说粒子对当前自身运动状态的信任程度,粒子依据自身的速度进行惯性运动。惯性权重使粒子保持运动的惯性和搜索扩展空间的趋势。w值越大,探索新区域的能力越强,全局寻优能力越强,但是局部寻优能力越弱。反之,全局寻优能力越弱,局部寻优能力强。较大的w有利于全局搜索,跳出局部极值,不至于陷入局部最优;而较小的w有利于局部搜索,让算法快速收敛到最优解。当问题空间较大时,为了在搜索速度和搜索精度之间达到平衡,通常做法是使算法在前期有较高的全局搜索能力以得到合适的种子,而在后期有较高的局部搜索能力以提高收敛精度,所以w不宜为一个固定的常数[3]。
当w=1时,退化成基本粒子群算法,当 w=0 时,失去对粒子本身经验的思考。推荐取值范围:[0.4,2],典型取值:0.9、1.2、1.5、1.8
改善惯性权重w
在解决实际优化问题时,往往希望先采用全局搜索,使搜索空间快速收敛于某一区域,然后采用局部精细搜索以获得高精度的解。因此提出了自适应调整的策略,即随着迭代的进行,线性地减小w的值。这里提供一个简单常用的方法——线性变化策略:随着迭代次数的增加,惯性权重w不断减小,从而使得粒子群算法在初期具有较强的全局收敛能力,在后期具有较强的局部收敛能力。
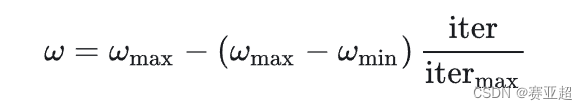

(5)学习因子: c1,c2
也称为加速系数或加速因子(这两个称呼更加形象地表达了这两个系数的作用)
c1 表示粒子下一步动作来源于自身经验部分所占的权重,将粒子推向个体最优位置
![]()
的加速权重;
c2表示粒子下一步动作来源于其它粒子经验部分所占的权重,将粒子推向群体最优位置
![]()
的加速权重;
c1=0:无私型粒子群算法,"只有社会,没有自我",迅速丧失群体多样性,易陷入局部最优而无法跳出;
c2=0:自我认知型粒子群算法,"只有自我,没有社会",完全没有信息的社会共享,导致算法收敛速度缓慢;
c1,c2都不为0:完全型粒子群算法,更容易保持收敛速度和搜索效果的均衡,是较好的选择。
低的值使粒子在目标区域外徘徊,而高的值导致粒子越过目标区域。 推荐取值范围:[0,4];典型取值:c1=c2=2、c1=1.6和 c2=1.8 、c1=1.6和 c2=2 ,针对不同的问题有不同的取值,一般通过在一个区间内试凑来调整这两个值。
1.8算法的一些重要概念和技巧
(1)适应值(fitness values)
即优化目标函数的值,用来评价粒子位置的好坏程度,决定是否更新粒子个体的历史最优位置和群体的历史最优位置,保证粒子朝着最优解的方向搜索。
(2)位置限制
限制粒子搜索的空间,即自变量的取值范围,对于无约束问题此处可以省略。
(3)速度限制
为了平衡算法的探索能力与开发能力,需要设定一个合理的速度范围,限制粒子的最大速度 vmax ,即粒子下一步迭代可以移动的最大距离。
1.9代码
clc
clear
close all
E=0.000001;
maxnum=800;%最大迭代次数
narvs=2;%目标函数的自变量个数
particlesize=50;%粒子群规模
c1=2;%每个粒子的个体学习因子,加速度常数
c2=2;%每个粒子的社会学习因子,加速度常数
w=0.6;%惯性因子
vmax=5;%粒子的最大飞翔速度
v=2*rand(particlesize,narvs);%粒子飞翔速度
x=-300+600*rand(particlesize,narvs);%粒子所在位置
%定义适应度函数
fitness=inline('(x(1)^2+x(2)^2)/10000','x');
for i=1:particlesize
f(i)=fitness(x(i,:));
end
personalbest_x=x;
personalbest_faval=f;
[globalbest_faval,i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:);
k=1;
while (k<=maxnum)
for i=1:particlesize
f(i)=fitness(x(i,:));
if f(i)<personalbest_faval(i)
personalbest_faval(i)=f(i);
personalbest_x(i,:)=x(i,:);
end
end
[globalbest_faval,i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:);
for i=1:particlesize
v(i,:)=w*v(i,:)+c1*rand*(personalbest_x(i,:)-x(i,:))...
+c2*rand*(globalbest_x-x(i,:));
for j=1:narvs
if v(i,j)>vmax
v(i,j)=vmax;
elseif v(i,j)<-vmax
v(i,j)=-vmax;
end
end
x(i,:)=x(i,:)+v(i,:);
end
ff(k)=globalbest_faval;
if globalbest_faval<E
break
end
% figure(1)
% for i= 1:particlesize
% plot(x(i,1),x(i,2),'*')
% end
k=k+1;
end
xbest=globalbest_x;
figure(2)
set(gcf,'color','white');
plot(1:length(ff),ff)