【数据结构】堆（C语言）

今天我们来学习堆，它也是二叉树的一种（我滴神树！）
在这里插入图片描述

堆的介绍：

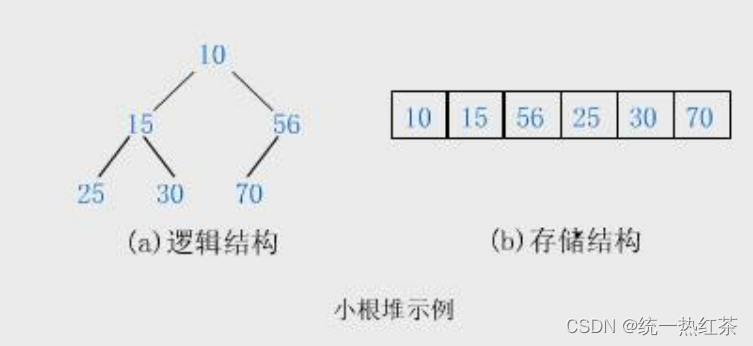
如果有一个关键码的集合K = { ，，，…， }，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足： <= 且
<= ( >= 且 >= ) i = 0，1，
2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质：

堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。

由于他们存储在数组中，又因为完全二叉树的性质，数组中不会空出来，故可以得到以下结论（皆为数组下标）：

parent = （child - 1）÷ 2
child（左孩子结点） = parent × 2 + 1
child（右孩子结点） = parent × 2 + 2

在这里插入图片描述

堆的代码实现：

堆的结构体创建：

typedef int HpDataType;

typedef struct Heap
{
	int size;
	int capacity;
	HpDataType* a;
}Hp;

堆的初始化：

这里我们选择先不给赋值，等push时再给赋值

void HpInit(Hp* php)
{
	assert(php);

	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

堆的销毁：

虽然与初始化相似，但是不能混用

void HpDestory(Hp* php)
{
	assert(php);

	free(php->a);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

堆的push：

我们需要一个向上调整算法：
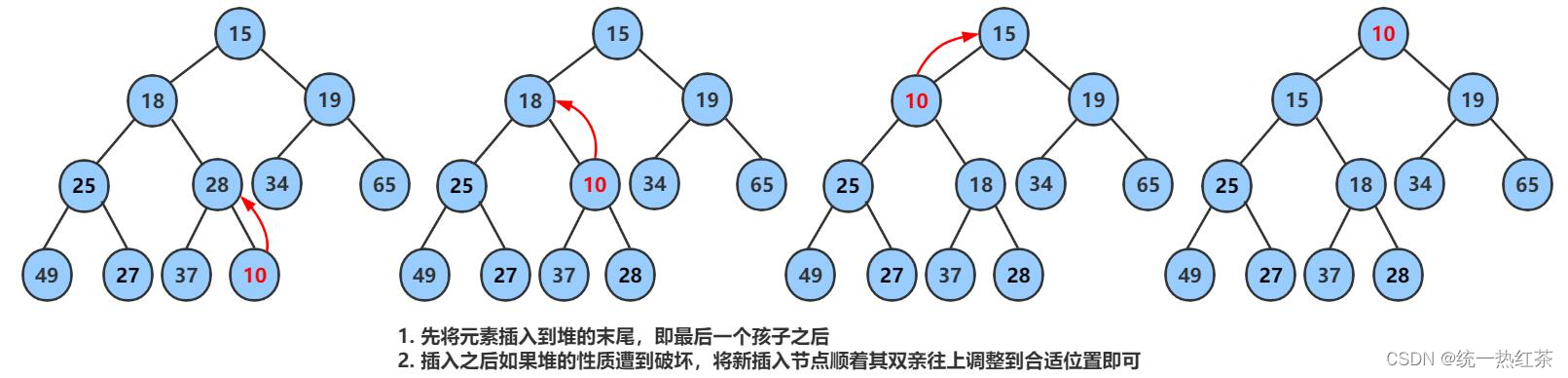
在这里插入图片描述
这里我们选择创建小堆

因为我们只有push需要创建newnode，故不需要重新封装一个CreatNewnode函数

void HpPush(Hp* php, HpDataType x)
{
	assert(php);

	if (php->capacity == php->size)
	{
		int newcapacity = (php->capacity == 0 ? 4 : php->capacity * 2);
		HpDataType* tmp = (HpDataType*)realloc(php->a, sizeof(HpDataType)* newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}

	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size - 1);
}

向上调整算法：

注意：
我们在进行向上传参时，要传入动态数组的地址和最后一个叶子节点的下标，为什么不是传入结构体的地址原因会在后来讲解

Swap(HpDataType* e1, HpDataType* e2)
{
	HpDataType tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

void AdjustUp(HpDataType* a, int child)
{
	int parent = (child - 1) / 2;
	//假设进入循环时child > 0
    //这里选择child = 0作为结束标志是因为当child = 0时
    //a[child] 与 a[parent]已经交换过一次了,
    //他们两现在同时指向下标位0，不需要在交换了
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
		}
		else
		{
			break;
		}

		child = (child - 1) / 2;
		parent = (parent - 1) / 2;
	}
}

堆的pop：

注意：
我们在进行pop时，并不是pop最后的叶子节点，这样没有实际意义，我们要pop的是根节点，这样是有实际意义的，比如Top k问题，堆排序等

pop主体部分：

void HpPop(Hp* php)
{
	assert(php);

	Swap(&php->a[php->size - 1], &php->a[0]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}

同理我们也需要一个向下调整算法
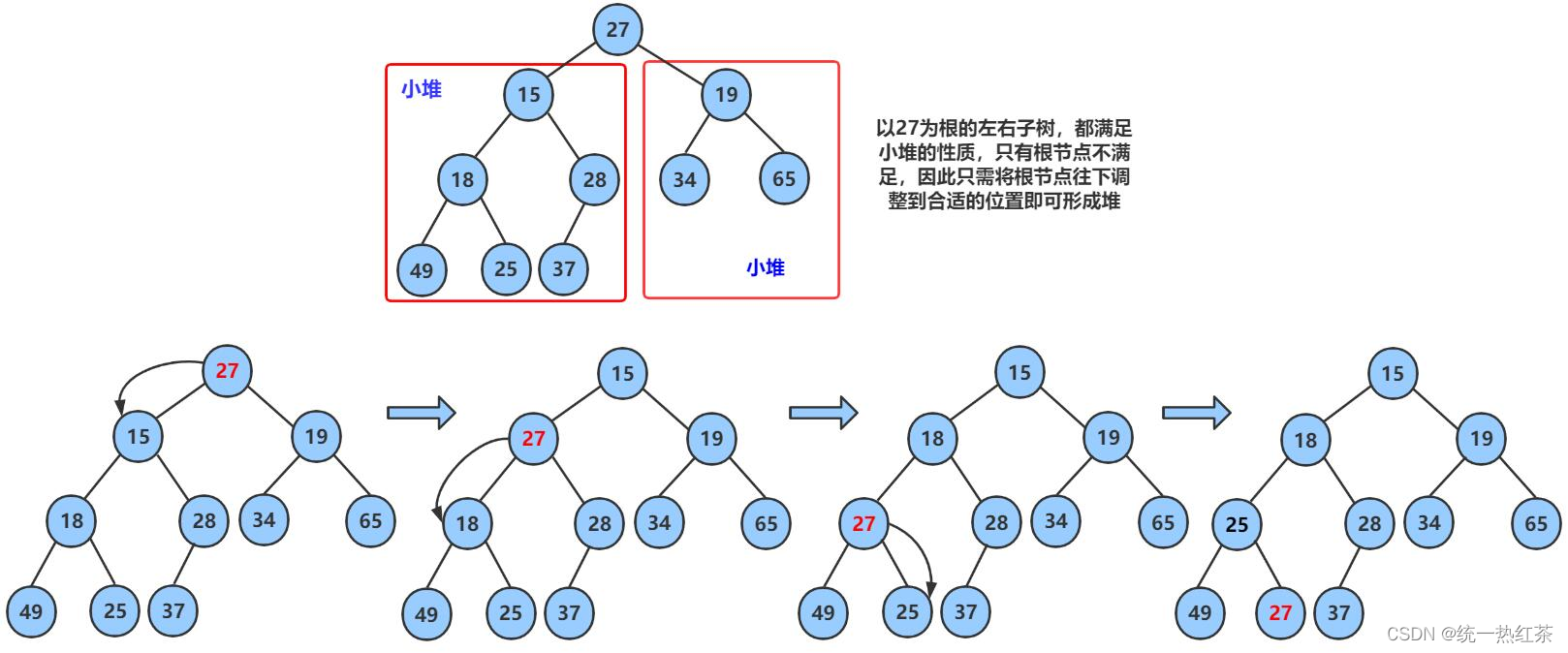
在这里插入图片描述
注意：

传参时仍然是传动态数组a的地址，另外还需要size与根节点0的下标，
size用于判断是否超出堆的范围，0作为parent的初始值

向下调整时我们需要找出孩子节点中较大或较小的那个，在这种情况下我们可以使用假设法，假设后在进行判断是否正确，将两段逻辑变成一段逻辑

AdjustDown(HpDataType* a, int size, int parent)
{
	//假设法
	int child = parent * 2 + 1;

	while (child < size)
	{
		if (child + 1 < size && a[child] > a[child + 1])
		{
			child++;
		}

		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);
		}
		else
		{
			break;
		}
		child = child * 2 + 1;
		parent = parent * 2 + 1;
	}
}

判空 && 求Top元素 && 求size：

bool HpEmpty(Hp* php)
{
	assert(php);

	return php->size == 0;
}

int HpTop(Hp* php)
{
	assert(php);
	//注意为空
	assert(php->size);

	return php->a[0];
}

int HpSize(Hp* php)
{
	assert(php);

	return php->size;
}

完整源码：

heap.c

#define _CRT_SECURE_NO_WARNINGS 1

#include"heap.h"

void HpInit(Hp* php)
{
	assert(php);

	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

void HpDestory(Hp* php)
{
	assert(php);

	free(php->a);
	php->a = NULL;
	php->size = 0;
}

Swap(HpDataType* e1, HpDataType* e2)
{
	HpDataType tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

void AdjustUp(HpDataType* a, int child)
{
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
		}
		else
		{
			break;
		}

		child = (child - 1) / 2;
		parent = (parent - 1) / 2;
	}
}
//小堆
void HpPush(Hp* php, HpDataType x)
{
	assert(php);

	if (php->capacity == php->size)
	{
		int newcapacity = (php->capacity == 0 ? 4 : php->capacity * 2);
		HpDataType* tmp = (HpDataType*)realloc(php->a, sizeof(HpDataType)* newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}

	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size - 1);
}

AdjustDown(HpDataType* a, int size, int parent)
{
	//假设法
	int child = parent * 2 + 1;

	while (child < size)
	{
		if (child + 1 < size && a[child] > a[child + 1])
		{
			child++;
		}

		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);
		}
		else
		{
			break;
		}
		child = child * 2 + 1;
		parent = parent * 2 + 1;
	}
}

void HpPop(Hp* php)
{
	assert(php);

	Swap(&php->a[php->size - 1], &php->a[0]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}

bool HpEmpty(Hp* php)
{
	assert(php);

	return php->size == 0;
}

int HpTop(Hp* php)
{
	assert(php);
	assert(php->size);

	return php->a[0];
}

int HpSize(Hp* php)
{
	assert(php);

	return php->size;
}

heap.h

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

typedef int HpDataType;

typedef struct Heap
{
	int size;
	int capacity;
	HpDataType* a;
}Hp;

void HpInit(Hp* php);

void HpDestory(Hp* php);

void HpPush(Hp* php, HpDataType x);

void HpPop(Hp* php);

bool HpEmpty(Hp* php);

int HpSize(Hp* php);

int HpTop(Hp* php);

有疑问可以及时找博主交流

目录