李群与李代数

旋转矩阵是一个正交且行列式为1的矩阵。
本文总结的是一些用在机器人slam中的李群李代数知识，并非数学专业，不够严谨见谅。

前言

本文设想你已经了解了旋转矩阵的知识，并且看过一些李群和李代数的资料，比如视觉slam十七四讲之类的，在此基础上我们试图抛开一些繁琐的公式推导，尽可能去描述一下李群李代数在干什么这件事。很明确的一点是，引入李代数是为了求导。
我们知道由旋转矩阵和乘法构成李群SO(3),通常在机器人位姿优化问题中需要求导，如：R=R+$\Delta R$，但是这样做显然是不对的，因为旋转的叠加是乘的关系如：R$\Delta R$，这也被描述为：SO(3)对加法不封闭。为了解决这个问题引入李代数。下面我们一起来看：

定义

群

群是一种集合加上一种运算的代数结构。 我们把集合记作A，运算记作.,那么群可以记作G=（A，.）。满足：封闭性、结合律、幺元及逆。

李群

李群是一种连续（光滑）的群。

李代数

李代数由一个集合V、一个数域F和一个二元运算[,]组成，记作（V，F，[,]）。 [,]称为李括号。满足:封闭性、双线性、自反性和雅可比等价。
eg:三维向量${\mathbb{R}}^3$上定义的x积是一种李括号 ，g=(${\mathbb{R}}^3$,$\mathbb{R}$,x)构成了李代数。

李群与李代数的关系

大致了解了李群李代数的定义后，我们重点来理解李群李代数的关系。
前面给出了李群李代数的基本定义，那么现在我们来看一下他们之间的关系，直接给出答案，一个SO(3)群，也就是三维特殊正交群，与他对应的李代数之间的关系为：
$$R=e^{{\varphi }^{\wedge }}$$ ${\varphi }^{\wedge }$是一个反对称矩阵，称作SO(3)的李代数。具体推导可以参考视觉slam14讲。
参考知乎上[如何通俗的解释李群和李代数的关系]这篇文章(https://www.zhihu.com/question/356466246/answer/2612548870)
其实李代数相当于定义在三维空间（球面)上绕定轴旋转运动时的速度， 速度方向与转轴和t时刻位矢呈法向， 也就球面上某点处所谓的切空间 ，这个球面的局部就叫流形。（大致就是这个意思，好吧，我也不是很懂，哈哈，但是不重要，只要知道了以上旋转矩阵和李代数的对应关系，那就接着往下看）。

李代数求导

知道了以上李群与李代数的指数映射关系，那么我们来看看求导问题：
通过R对空间中一点p进行旋转得到Rp,求旋转后的导数
$$\frac{\partial Rp}{\partial R}$$
由于R对加法不封闭，转化为为李代数$\varphi$求导，$\varphi$是反对称矩阵对应的向量，对加法是封闭的。为：
$$\frac{\partial e^{{\varphi }^{\wedge }}p}{\partial \varphi }$$
最终这个式子的解为：

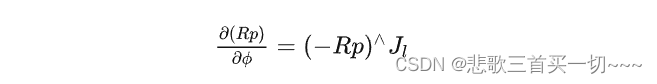
$J_l$为左雅可比，具体参考BCH公式。

扰动模型

以上我们求出了旋转后点想对于李代数的导数，但是$J_l$还是有点复杂，于是我们引入扰动模型（左乘）

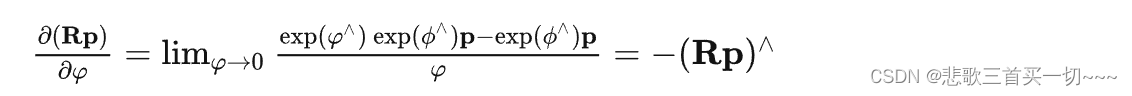
总之，就是引入李代数然后通过一堆近似的方法，让求导尽可能变得简单。

参考
视觉slam十四讲 高翔
李狗嗨，“如何通俗地解释李群和李代数的关系？”，https://www.zhihu.com/question/3564
李群和李代数 —— 名字听起来很猛其实也没那么复杂 https://zhuanlan.zhihu.com/p/358455662