数据结构——顺序表
前言
本篇为数据结构系列的第一篇文章,数据结构是一种有效地存储和管理数据的方法,在应对实际问题时的重要性不亚于算法。本系列为我在学习数据结构后对于数据结构的理解,使用的语言为C。这里提几点建议,数据结构最重要的是思想,先有思路再进行代码还原能提高学习效率,在学习时,建议多画图辅助理解,图形能更直观地表达出数据结构。
1 顺序表的基本思路
顺序表,又称线性表,是一种基础的线性数据结构。其基本思路是在一段连续的内存空间上存储数据。
1.1 静态版顺序表
顺序表的基本思路是将数据存储在一段连续的内存空间上,这与C语言数据类型中的数组非常相似,因此我们可以通过数组来实现一个顺序表。
当然,当我们创建一个数组作为顺序表后,需要存储的数据量可能会小于数组的大小,这时数组中就有部分未使用的空间。因此,在顺序表中最好有一个变量来管理顺序表有效空间的大小。如下为一个简单的静态顺序表结构。
struct SeqList
{
int a[100]; //容量大小为100个整型的顺序表
int size;
};在这样一个顺序表结构中,结构成员a即顺序表主体,用于存储数据。而变量size则负责管理有效空间,其初始值应该为0,表明初始有效空间为0,即顺序表中的数据量为0。
由于数组大小直接给定,因此这个顺序表的容量已经确定,无法改变,我们把这种无法改变容量的顺序表称为静态顺序表。
下图为静态顺序表的图解(矩形中的数字代表存储在表中的整型数据)。

1.2 动态版顺序表
与静态顺序表相反,动态顺序表的容量大小可以通过动态内存分配来管理。与静态版相比,动态版顺序表使用起来更加灵活,能更好地适应实际情况,提高内存空间的利用率(大部分数据结构基本都使用动态内存管理)。如下为一个简单的动态顺序表结构。
struct SeqList
{
int* a;
int size;
int capacity;
};与静态顺序表相比,动态顺序表结构中的主体a变成了指针类型。其实很好理解,学了数组后我们知道,数组本质上也是通过数组初始位置的指针来管理数组,这里用指针替换主要是方便进行动态内存管理。另外,多出了一个变量capacity,用来管理顺序表的容量,当容量不够大时,可使用realloc函数进行扩容。
下图为动态顺序表的图解。

2 顺序表的实现
2.1 接口
对于比较复杂的项目,我们采用接口,即在一个头文件中包含所有该项目所需要的标识符声明,以便完工后使用,在数据结构中也如此。
在写接口前,我们需要先分析该项目所需具备的功能,并分模块实现。
接下来我们来分析顺序表所需的功能。首先,当我们创建一个顺序表时,需要对顺序表进行初始化,包括为顺序表动态开辟初始空间,设置初始容量,设置初始有效容量为0等。相对的,既然进行了动态内存开辟,那么在空间使用完毕后就要释放空间。其次,就是实现顺序表作为数据结构的基本功能,数据的增删查改。
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#define SeqListAdd 2
typedef int SLDataType;
typedef struct SeqList
{
SLDataType* a;
int size;
int capacity;
}SeqList;
// 对数据的管理:增删查改
void SeqListInit(SeqList* ps);
void SeqListDestroy(SeqList* ps);
void SeqListPrint(SeqList* ps);
void SeqListPushBack(SeqList* ps, SLDataType x);
void SeqListPushFront(SeqList* ps, SLDataType x);
void SeqListPopFront(SeqList* ps);
void SeqListPopBack(SeqList* ps);
// 顺序表查找
int SeqListFind(SeqList* ps, SLDataType x);
// 顺序表在pos位置插入x
void SeqListInsert(SeqList* ps, int pos, SLDataType x);
// 顺序表删除pos位置的值
void SeqListErase(SeqList* ps, int pos);上方为我所用的顺序表接口。其中使用typedef将int重命名为SLDataType是为了后续调用方便。当使用者需要使用该顺序表存储其它数据类型的数据时,仅需将其中的int改为所需类型即可。
2.2 初始化
初始化的思路其实已经很明确了,首先动态开辟一块初始空间,用于存储数据。开辟空间后,我们就需要设置初始有效空间大小和初始容量大小。
我们先来看图解,我们以初始化开辟两个整型大小空间为例。首先,我们动态开辟大小为2的空间,并将空间的首地址赋值于顺序表结构中的指针变量a,然后,由于初始状态下顺序表中肯定是没有存放数据的,因此有效空间大小为0,即结构中的size为0。而由于例子中初始开辟的空间大小为2,因此初始容量为2,即结构中的capacity为2。

接下来是代码实现,首先使用malloc函数开辟2个整型大小的空间(SeqListAdd为接口中定义的常量,大小为2),然后这里判断开辟是否成功,若空间开辟失败则使用perror函数打印错误信息,这样做是为了方便我们快速找到出错位置。然后将size赋值为0,capacity赋值为SeqListAdd,初始化完成。
void SeqListInit(SeqList* ps)
{
assert(ps);
ps->a = (SLDataType*)malloc(sizeof(SLDateType) * SeqListAdd);
if (ps->a == NULL) //动态内存开辟失败
{
perror("Init:malloc"); //报错
return;
}
ps->size = 0;
ps->capacity = SeqListAdd;
}2.3 插入数据
数据结构的功能就是存储数据,那么既然我们已经初始化完毕,那么下一步我们就要将数据存入结构中,这就是增删查改中的增。
线性数据结构的插入数据一般分为头部插入(简称头插),尾部插入(简称尾插)和随机位置插入。
2.3.1 尾部插入
顺序表的尾插非常简单,首先我们需要明确一点,顺序表的size变量的数值就是顺序表尾部数据的下一个位置的下标。这一点我在之前的图片中也表达了,尾部数据的下标为size-1。也就是说,当我们进行尾插时,只需要将数据插入下标为size的位置即可,如图。

当然,在插入数据之前,我们需要考虑一个问题,那就是容量是否足够。若容量不足,则会出现非法访问的情况,如下图。

为了避免这种情况的发生,在插入数据之前,我们应该先进行容量检查,若容量不足,则先进行扩容,再执行插入。
这就是顺序表尾部插入的基本思路了,接下来我们来看代码。
函数的参数x为需要插入顺序表的新数据。首先进行容量检查,容量检查的思路是判断size与capacity的大小是否相等,若相等则说明顺序表已满(这是一个规律,可通过观察得到),需要先扩容再进行数据插入。否则可直接插入。根据之前的分析得出,新的数据应该插入下标为size的位置,插入完毕后,由于插入了一个新数据,顺序表的有效空间+1,因此让size自增1。
void SeqListPushBack(SeqList* ps, SLDataType x)
{
assert(ps);
if (ps->size == ps->capacity)
{
ps->capacity += SeqListAdd;
ps->a = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * ps->capacity);
}
if (ps->a == NULL)
{
perror("PB:realloc");
return;
}
ps->a[ps->size++] = x;
}2.3.2 头部插入
顺序表的头插相对来说比较麻烦,由于realloc函数无法实现向前扩容,因此想要在顺序表的头部腾出一个空间来进行头插就必须将表中所有元素向后移动一位。
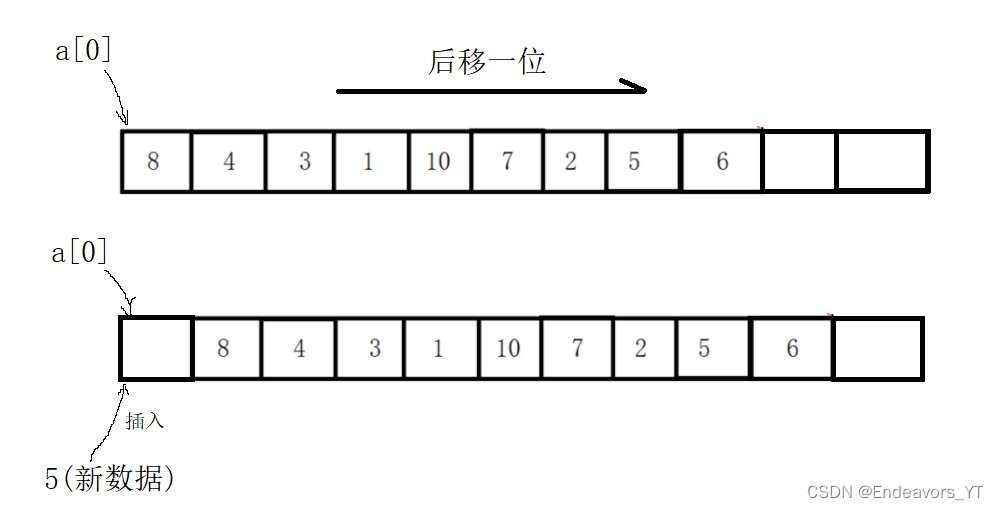
同样地,我们来进行步骤分析。首先当然是进行容量检查。然后则是将所有数据向后移动,这个操作相信大家都非常熟悉,通过简单的循环遍历就能实现。最后将表中首元素赋值为新数据即可。
我们来看代码。
检查容量的部分我就不多说了,我们直接来看数据后移的部分。这里我采用一个for循环,从下标为size-1处开始移动数据,也就是从顺序表的尾部开始移动,这样做是为了防止前面的数据移动覆盖后面的数据。移动完成后,插入数据,size自增1。
void SeqListPushFront(SeqList* ps, SLDataType x)
{
assert(ps);
if (ps->size == ps->capacity)
{
ps->capacity += SeqListAdd;
ps->a = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * ps->capacity);
}
if (ps->a == NULL)
{
perror("PF:realloc");
return;
}
int i = 0;
for (i = ps->size; i > 0; i--)
{
ps->a[i] = ps->a[i - 1];
}
ps->a[i] = x;
ps->size++;
}关于随机位置插入我会在查找数据部分详细介绍。
2.4 删除数据
有了插入数据,对应的就有删除数据,不可能只准进不准出,那不是无期徒刑了吗。与插入数据类似的,删除数据也分为头部删除(头删),尾部删除(尾删)和随机位置删除。
2.4.1 尾部删除
同样地,我们先从尾部删除讲起。与插入相比,删除数据可简单的多,因为删除数据不需要考虑容量是否足够,不可能越删除数据越多吧(除非你写出bug)。
可能大部分新手都会认为删除数据就必须将数据从表里抹除,例如把原数据用0覆盖,但其实这样并没有达到删除的效果,顶多算是修改数据。这里我们想想尾删是需要达到什么效果,将尾部的元素移出顺序表,并使有效空间减一。那不就很简单了吗,让size自减1就行了。size变量的值代表有效空间的大小,size自减1就是有效空间减少了1。而size自减1刚好又使原本处于尾部的元素离开了有效空间的范围,也就是无法再顺序表的有效空间找到,这就达到了我们的目的。
来看图解和代码。


void SeqListPopBack(SeqList* ps)
{
assert(ps && ps->size);
ps->size--;
}需要注意的是,当顺序表中没有数据时,也就是size为0时,理论上不能进行删除操作,因此我用assert函数断言size的值不为0以确保顺序表中有数据。
可以看出,实际上尾删只改变了size的值,并不是真的将尾部的数据抹除。那么这样做会不会影响后续尾插的数据呢?当然不会,看我们之前尾插的代码可以知道,尾插是通过赋值的方式插入数据,会直接覆盖原有数据,因此不会造成影响。
2.4.2 头部删除
头删的大体思路与尾删相似,也是使size自减1,但是由于我们需要删除头部的数据,不能直接自减,而是要将头部数据后的数据全部前移一位。
头删的图解如下。


至于头删后多出一个6这是因为数据前移是通过赋值实现,因此本来处在尾部的数据并未被抹去,不过由于其已经不在有效空间内,因此不会对其它操作产生影响。
接下来看代码。
void SeqListPopFront(SeqList* ps)
{
assert(ps && ps->size);
int i = 0;
for (i = 0; i < ps->size; i++)
{
ps->a[i] = ps->a[i + 1];
}
ps->size--;
}关于随机位置删除我会在查找数据部分详细介绍。
2.5 查找数据
数据结构的功能之一是存储数据,但是存储数据是为了更好地管理和使用数据。对于一个已经存有大量数据的顺序表,我们应该如何从中获取我们需要的数据呢?这就需要实现查找数据。
2.5.1 查找数据
这里仅介绍简单的顺序遍历查找顺序表中第一个所求数据。对给定的所求数据,通过顺序遍历顺序表找到该数据,并返回其在顺序表中的下标,若没找到则返回-1。这就是查找数据的基本思路,接下来看图解和代码。


int SeqListFind(SeqList* ps, SLDataType x)
{
assert(ps);
int i = 0;
for (i = 0; i < ps->size; i++)
{
if (ps->a[i] == x)
return i;
}
return -1;
}2.5.2 随机位置插入与删除
随机位置插入就是在给定的随机位置插入数据,其大致思路与头插类似,需要将插入位置后的数据向后移动一位。而随机位置删除也与头删类似,将给定随机位置后的数据向前移动一位,覆盖该位置原始数据即可。
通常,我们通过给定随机位置的下标来确定一个随机位置。而我们知道,查找函数的返回值就是所求数据的下标,因此我们通常将它们结合起来使用。
由于大致操作与头插和头删相同,重复操作我就不展开介绍了,直接来看图解和代码。


void SeqListInsert(SeqList* ps, int pos, SLDataType x)
{
assert(ps);
assert(pos >= 0);
if (ps->size == ps->capacity)
{
ps->capacity += SeqListAdd;
ps->a = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * ps->capacity);
}
if (ps->a == NULL)
{
perror("Insert:realloc");
return;
}
int i = 0;
for (i = ps->size; i > pos; i--)
{
ps->a[i] = ps->a[i - 1];
}
ps->a[i] = x;
ps->size++;
}

void SeqListErase(SeqList* ps, int pos)
{
assert(ps && ps->size);
int i = 0;
for (i = pos; i < ps->size - 1; i++)
{
ps->a[i] = ps->a[i + 1];
}
ps->size--;
}2.6 销毁
由于我们动态开辟了空间,当我们使用完顺序表后最好将其释放,以免造成内存泄露,我们把这个操作称为顺序表的销毁。
那么相信对于顺序表的销毁相信大家已经明白要如何操作了。由于我们动态开辟的空间是通过顺序表结构中的指针变量a维护的,因此我们只需要将a作为参数传入free函数即可。
void SeqListDestroy(SeqList* ps)
{
assert(ps && ps->a);
free(ps->a);
ps->a = NULL;
}3 其它
3.1 打印顺序表
打印顺序表在实际应用中的意义不大,一般用于测试时方便观察。实现也非常简单,遍历打印即可
void SeqListPrint(SeqList* ps)
{
assert(ps);
int i = 0;
for (i = 0; i < ps->size; i++)
{
printf("%d\n", ps->a[i]);
}
}3.2 容量检查函数复用
由于所有的插入操作中都涉及到容量检查这一操作,因此我们可以单独封装一个函数来实现这一操作,以简化代码。
void CapacityCheck(SeqList* ps)
{
assert(ps);
if (ps->size == ps->capacity)
{
ps->capacity += SeqListAdd;
ps->a = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * ps->capacity);
}
}
void SeqListPushBack(SeqList* ps, SLDataType x)
{
assert(ps);
CapacityCheck(ps);
if (ps->a == NULL)
{
perror("PB:realloc");
return;
}
ps->a[ps->size++] = x;
}
3.3 插入、删除函数复用
由于插入、删除的思路都一样,因此在头插和尾插时,我们可以直接复用随机插入函数。同理,进行头删和尾删时,可以直接复用随机删除函数。
void SeqListPushBack(SeqList* ps, SLDataType x)
{
assert(ps);
CapacityCheck(ps);
if (ps->a == NULL)
{
perror("PB:realloc");
return;
}
SeqListInsert(ps, ps->size, x);
}
void SeqListPushFront(SeqList* ps, SLDataType x)
{
assert(ps);
CapacityCheck(ps);
if (ps->a == NULL)
{
perror("PF:realloc");
return;
}
SeqListInsert(ps, 0, x);
}结束语
以上就是有关顺序表结构的全部内容啦,若内容有误欢迎各位大佬批评指正,有哪部分内容没有表达清楚也可以提问哦。再次强调,数据结构学习最好的方法就是画图理解,观察图形可比用脑子空想高效。另外,顺序表的源码我都藏在文中了,大家自行寻找吧!