(分子优化BenchMark)Sample Efficiency Matters: A Benchmark for Practical Molecular Optimization(PMO)
code and paper: https://arxiv.org/abs/2206.12411
SMILES的benchmark:
【13】GuacaMol: Benchmarking Models for De Novo Molecular Design:GuacaMol: Benchmarking Models for De Novo Molecular Design | Papers With Code
【25】BOSS: Bayesian Optimization over String Spaces:BOSS: Bayesian Optimization over String Spaces | Papers With Code
【6】Automatic chemical design using a data-driven continuous representation of molecules:Automatic chemical design using a data-driven continuous representation of molecules | Papers With Code
【5】Molecular De Novo Design through Deep Reinforcement Learning:Molecular De Novo Design through Deep Reinforcement Learning | Papers With Code
2 Algorithms
A molecular optimization method has two major components:
(1) a molecular assembly strategy that defines the chemical space by assembling a digital representation of compounds, and(用什么形式去表示这些分子)
(2) an optimization algorithm that navigates this chemical space.
This section will first introduce common strategies to assemble molecules, then introduce the benchmarked molecular optimization methods based on the core optimization algorithms. Table 1 summarizes current molecular design methods categorized based on assembly strategy and optimization method, including but not limited to the methods included in our baseline. We emphasize that our goal is not to make an exhaustive list but to include a group of methods that are representative enough to obtain meaningful conclusions.
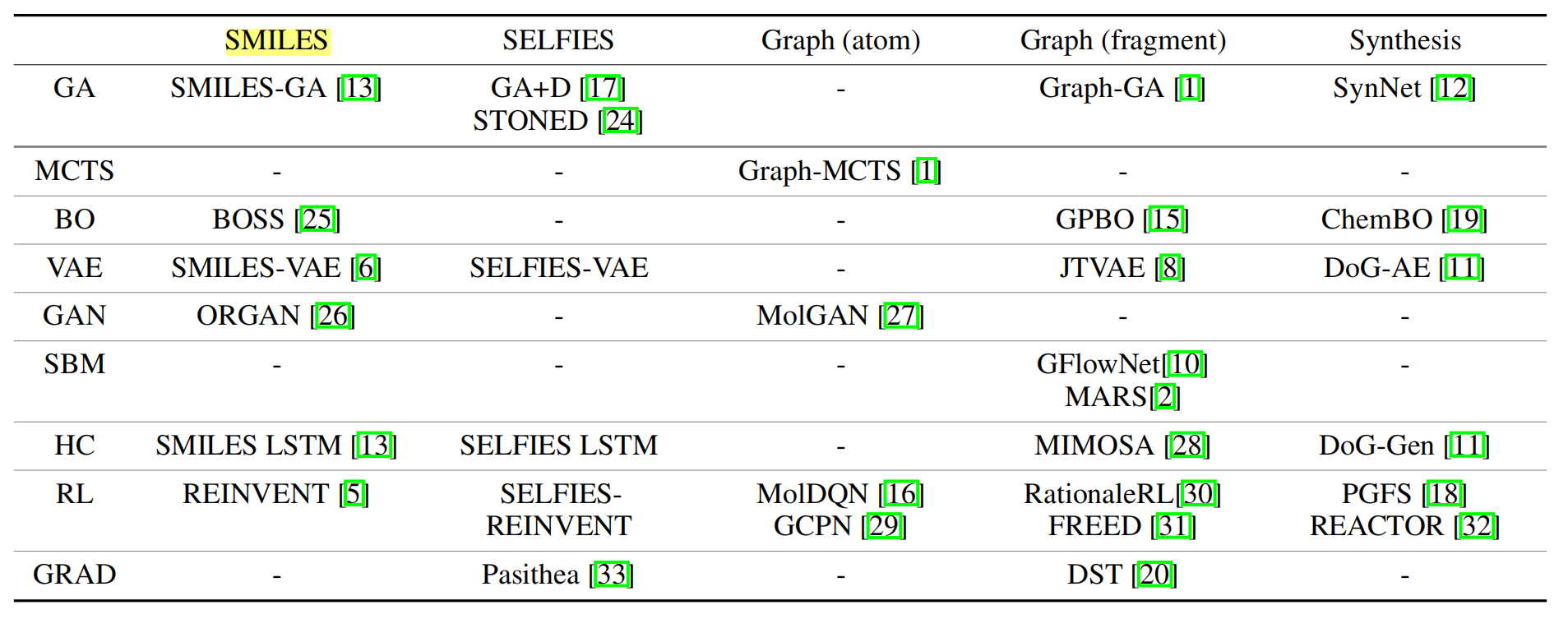
Table 1: Representative molecule generation methods, categorised based on the molecular assembly strategies and the optimization algorithms. Columns are various molecular assembly strategies while rows are different optimization algorithms.
2.1 Preliminaries(预备知识)
In this paper, we limit our scope to general-purpose single-objective molecular optimization methods focusing on small organic molecules with scalar properties with some relevance to therapeutic design. Formally, we can formulate such a molecular design problem as an optimization problem:
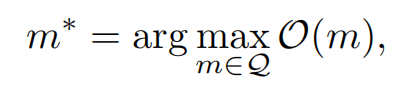
where m is a molecular structure, Q demotes the design space called chemical space that comprises all possible candidate molecules. The size of Q is impractically large, e.g., 1060 [23]. We assume we have access to the ground truth value of a property of interest denoted by O(m) : Q → R, where an oracle, O, is a black-box function that evaluates certain chemical or biological properties of a molecule m and returns the ground truth property O(m) as a scalar.
2.2 Molecular assembly strategies
String-based.
String-based assembly strategies represent molecules as strings and explore chemical space by modifying strings directly: character-by-character, token-by-token, or through more complex transformations based on aspecific grammar. We include two types of string representations: (1) Simplified Molecular-Input Line-Entry System (SMILES) [34], a linear notation describing the molecular structure using short ASCII strings based on a graph traversal algorithm; (2) SELF-referencIng Embedded Strings (SELFIES) [9], which avoids syntactical invalidity by enforcing the chemical validity rules in a formal grammar table.
Graph-based.
Two-dimensional (2D) graphs can intuitively define molecular identities to a first approximation (ignoring stereochemistry): the nodes and edges represent the atoms and bonds. There are two main assembling strategies for molecular graphs:
(1) an atom-based assembly strategy [16] that adds or modifies atoms and bonds one at a time, which covers all valid chemical space;
(2) a fragment-based assembling strategy [8] that summarizes common molecular fragments and operates one fragment at a time. Note that fragment-based strategy could also include atom-level operation.
Synthesis-based.
Most of the above assembly strategies can cover a large chemical space, but an eventual goal of molecular design is to physically test the candidate; thus, a desideratum is to explore synthesizable candidates only. Designing molecules by assembling synthetic pathways from commercially-available starting materials and reliable chemical transformation adds a constraint of synthesizability to the search space. This class can be divided into template-free [11] and template-based [12] based on how to define reliable chemical transformations, but we will not distinguish between them in this paper as synthesis-based strategy is relatively less explored in general.
2.3 Optimization algorithms
Screening (a.k.a. virtual screening)【虚拟筛选】 involves searching over a pre-enumerated library of molecules exhaustively. We include Screening as a baseline, which randomly samples ZINC 250k [35]. Model-based screening (MolPAL) [3] instead trains a surrogate model and prioritizes molecules that are scored highly by the surrogate to accelerate screening. We adopt the implementation from the original paper and treat it as a model-based version of screening.
Genetic Algorithm (GA) 【遗传算法】is a popular heuristic algorithm inspired by natural evolutionary processes. It combines mutation and/or crossover perturbing a mating pool to enable exploration in the design space. We include SMILES GA [36] that defifines actions based on SMILES context-free grammar and a modifified version of STONED [24] that directly manipulates tokens in SELFIES strings. Unlike the string-based GAs that only have mutation steps, Graph GA [1] derives crossover rules from graph matching and includes both atom- and fragment-level mutations. Finally, we include SynNet [12] as a synthesis-based example that applies a genetic algorithm on binary fifingerprints and decodes to synthetic pathways. We adopt the implementation of SMILES GA and Graph GA from Guacamol [13], STONED, and SynNet from the original paper. We also include the original implementation of a deep learning enhanced version of SELFIES-based GA from [17] and label it as GA+D.
Monte-Carlo Tree Search (MCTS)【蒙特卡洛树搜索 】 locally and randomly searches each branch of the current state (e.g., a molecule or partial molecule) and selects the most promising ones (those with highest property scores) for the next itera-tion. Graph MCTS [1] is an MCTS algorithm based on atom-level searching over molecular graphs. We adopt the implementation from Guacamol [13].
Bayesian optimization (BO) 【贝叶斯优化】[37] is a large class of method that builds a surrogate for the objective function using a Bayesian machine learning technique, such as Gaussian process (GP) regression, then uses an acquisition function combining the surrogate and uncertainty to decide where to sample, which is naturally model-based. However, as BO usually leverages a non-parametric model, it scales poorly with sample size and feature dimension [38]. We included a string-based model, BO over String Space (BOSS) [25], and a synthesis-based model, ChemBO [19], but do not obtain meaningful results even with early stopping (see Section B.3 for early stopping setting, and Section B.33 for more analysis). Finally, we adopt Gaussian process Bayesian optimization (GP BO) [15] that optimizes the GP acquisition function with Graph GA methods in an inner loop. The implementation is from the original paper, and we treat it as a model-based version of Graph GA.
Variational autoencoders (VAEs) 【变分自编码器】[39] are a class of generative method that maximize a lower bound of the likelihood (evidence lower bound (ELBO)) instead of estimating the likelihood directly. A VAE typically learns to map molecules to and from real space to enable the indirect optimization of molecules by numerically optimizing latent vectors, most commonly with BO. SMILES-VAE [6] uses a VAE to model molecules represented as SMILES strings, and is implemented in MOSES [40]. We adopt the identical architecture to model SELFIES strings and denote it as SELFIES-VAE. JT-VAE [8] abstracts a molecular graph into a junction tree (i.e., a cycle-free structure), and design message passing network as the encoder and tree-RNN as the decoder. DoG-AE [11] uses Wasserstein autoencoder (WAE) to learn the distribution of synthetic pathways.
Score-based modeling (SBM)【基于得分的模型】 formulates the problem of molecule design as a sampling problem where the target distribution is a function of the target property, featured by Markov-chain Monte Carlo (MCMC) methods that construct Markov chains with the desired distribution as their equilibrium distribution. MARkov molecular Sampling (MARS) [2] is such an example that leverages a graph neural network to propose action steps adaptively in an MCMC with an annealing scheme. Generative Flow Network (GFlowNet) [10] views the generative process as a flflow network and trains it with a temporal difference-like loss function based on the conservation of flflow. By matching the property of interest with the volume of the flflow, generation can sample a distribution proportional to the target distribution.
Hill climbing (HC)【爬山法】 is an iterative learning method that incorporates the generated high-scored molecules into the training data and fifine-tunes the generative model for each iteration. It is a variant of the cross-entropy method [41], and can also be seen as a variant of REINFORCE [42] with a particular reward shaping. We adopt SMILES-LSTM-HC from Guacamol [13] that leverages a LSTM to learn the molecular distribution represented in SMILES strings, and modififies it to a SELFIES version denoted as SELFIES-LSTM-HC. MultI-constraint MOlecule SAmpling (MIMOSA) [28] leverages a graph neural network to predict the identity of a masked fragment node and trains it with a HC algorithm. DoG-Gen [11] instead learn the distribution of synthetic pathways as Directed Acyclic Graph (DAGs) with an RNN generator.
Reinforcement Learning (RL)【强化学习】 learns how intelligent agents take actions in an environment to maximize the cumulative reward by transitioning through different states. In molecular design, a state is usually a partially generated molecule; actions are manipulations at the level of graphs or strings; rewards are defifined as the generated molecules’ property of interest. REINVENT [5] adopts a policy-based RL approach to tune RNNs to generate SMILES strings. We adopt the implementation from the original paper, and modify it to generate SELFIES strings, SELFIES-REINVENT. MolDQN [16] uses a deep Q-network to generate molecular graph in an atom-wise manner.
Gradient ascent (GRAD)【梯度上升】 methods learn to estimate the gradient direction based on the landscape of the molecular property over the chemical space, and back-propagate to optimize the molecules. Pasithea [33] exploits an MLP to predict properties from SELFIES strings, and back-propagate to modify tokens. Differentiable scaffolding tree (DST) [20] abstracts molecular graphs to scaffolding trees and leverages a graph neural network to estimate the gradient. We adopted the implementation from the original papers and modify them to update the surrogates online as data are acquired.
3 Experiments
3.1 Benchmark setup
This section introduces the setup of PMO benchmark. The main idea behind PMO is the pursuit of an ideal de novo molecular optimization algorithm that exhibits strong optimization ability, sample efficiency, generalizability to various optimization objectives, and robustness to hyperparameter selection and random seeds.
Oracle: To examine the generalizability of methods, we aim to include a broad range of pharmaceutically-relevant oracle functions. Systematic categorization of oracles based on their landscape is still challenging due to the complicated relationship between molecular structure and function.
We have included the most commonly used oracles (see a recent discussion of commonly-used oracles in [43]). Several have been described as “trivial”, but we assert this is only true when the number of oracle queries is not controlled. In total, PMO includes 23 oracle functions: QED [22], DRD2 [5], GSK3β, JNK3 [44], and 19 oracles from Guacamol [13].
1、QED is a relatively simple heuristic function that estimates if a molecule is likely to be a drug based on if it contains some “red flags”.(QED根据分子是否含有“红旗”来评估它是否是一种药物)
2、DRD2, GSK3β, and JNK3 are machine learning models (support vector machine (SVM), random forest (RF)) fit to experimental data to predict the bioactivities against their corresponding disease targets.(它们拟合实验数据以预测针对其相应疾病靶标的生物活性)
3、Guacamol oracles are designed to mimic the drug discovery objectives based on multiple considerations, called multi-property objective (MPO), including similarity to target molecules, molecular weights, CLogP, etc.
All oracle scores are normalized from 0 to 1, where 1 is optimal. Recently, docking scores that estimate the binding affinity between ligands and proteins have been adopted as oracles [45, 14, 46]. However, as the simulations are more costly than above ones but are still coarse estimates that do not reflect true bioactivity, we leave it to future work.
Metrics: To consider the optimization ability and sample efficiency simultaneously, we report the area under the curve (AUC) of top-K average property value versus the number of oracle calls (AUC top-K) as the primary metric to measure the performance. Unlike using top-K average property, AUC rewards methods that reach high values with fewer oracle calls. We use K = 10 in this paper as it is useful to identify a small number of distinct molecular candidates to progress to later stages of development. We limit the number of oracle calls to 10000, though we expect methods to optimize well within hundreds of calls when using experimental evaluations. The reported values of AUCs are min-max scaled to [0, 1].
Data: Whenever a database is required, we use ZINC 250K dataset that contains around 250K molecules sampled from the ZINC database [35] for its pharmaceutical relevance, moderate size, and popularity. Screening and MolPAL search over this database; generative models such as VAEs, LSTMs are pretrained on this database; fragments required for JT-VAE, MIMOSA, DST are extracted from this database.
Other details: We tuned hyperparameters for most methods on the average AUC Top-10 from 3 independent runs of two Guacamol tasks: zaleplon_mpo and perindopril_mpo. Reported results are from 5 independent runs with various random seeds. All data, oracle functions, and metric evaluations are taken from the Therapeutic Data Commons (TDC) [14] (https://tdcommons.ai) and more details are described in Appendix.
3.2 Results & Analysis
The primary results are summarized in Table 2 and 3. For clarity, we only show the ten best-performing models in the table. We show a selective set of optimization curves in Figure 1. The remaining results are in the Appendix A and D.
Sample efficiency matters. A first observation from the results is that none of the methods can optimize the simple toy objectives within hundreds of oracle calls, except some trivial ones like QED, DRD2, and osimertinib_mpo, which emphasize the need for more efficient molecular optimization algorithms. By comparing the ranking of AUC Top-10 and Top-10, we notice some methods have significantly different relative performances. For example, SMILES LSTM HC, which used to be seen as comparable to Graph GA, actually requires more oracle queries to achieve the same levelof performance, while a related algorithm, REINVENT, requires far fewer (see Figure 1). These differences indicate the training algorithm of REINVENT is more efficient than HC, emphasizing the importance of AUC Top-10 as an evaluation metric. In addition, methods that assemble molecules either token-by-token or atom-by-atom from a single start point, such as GA+D, MolDQN, and Graph MCTS, are most data-ineffificient. Those methods potentially cover broader chemical space and include many undesired candidates, such as unstable or unsynthesizable ones, which wastes a significant portion of the oracle budget and also imposes a strong requirement on the oracles’ quality.
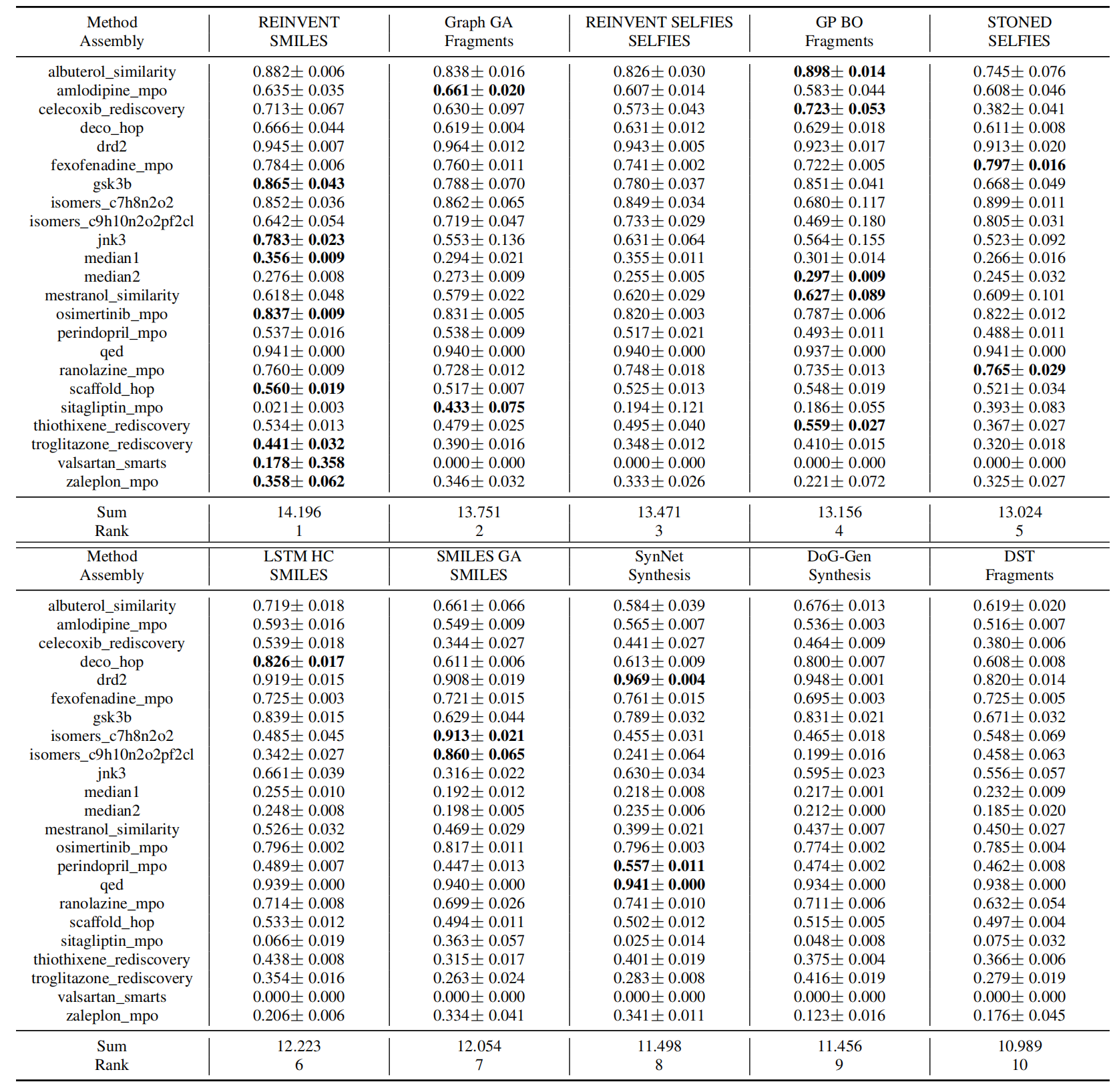
Table 2: Performance of ten best performing molecular optimization methods based on mean AUC Top-10. We report the mean and standard deviation of AUC Top-10 from 5 independent runs. The best model in each task is labeled bold. Full results are in the Appendix A
There are no obvious shortcomings of SMILES.
SELFIES was designed as a substitute of SMILES to solve the syntactical invalidity problem met in SMILES representation and has been adopted by a number of recent studies. However, our head-to-head comparison of string-based methods, especially the ones leveraging language models, shows that most SELFIES variants cannot outperform their corresponding SMILES-based methods in terms of optimization ability and sample efficiency (Figure 2a). We do observe some early methods like the initial version of SMILES VAE [6] (2016) and ORGAN [26] (2017) struggle to propose valid SMILES strings, but this is not an issue for more recent methods. We believe this is because current language models are better able to learn the grammar of SMILES strings, which has flattened the advantage of SELFIES. Further, as shown in Appendix D.1, more combinations of SELFIES tokens don’t necessarily explore larger chemical space but might map to a small number of valid molecules that can be represented by truncated SELFIES strings, which implies that there are still syntax requirements in generating SELFIES strings to achieve effective exploration.
On the other hand, we observe a clear advantage of SELFIES-based GA compared to SMILES-based one, which indicates that SELFIES has an advantage over SMILES when we need to design the rules to manipulate the sequence. However, we should note that the comparison is not head-to-head, as GAs’ performances highly depend on the mutation and crossover rule design, but not the representation. Graph GA’s mutation rules are also encoded in SMARTS strings and operate on SMILES strings, which can also be seen as SMILES modification steps. Overall, when we need to design the generative action manually, the assembly strategy that could derive desired transformation more intuitively should be preferred.
Our primary observations are that
(1) methods considered to be strong baselines, like LSTM HC, may be inefficient in data usage;
(2) several older methods, like REINVENT and Graph GA, outperform more recent ones;
(3) SELFIES does not seem to offer an immediate benefit in optimization performance compared to SMILES except in GA;
(4) model-based methods have the potential to be more sample efficient but require careful design of the inner-loop, outer-loop, and the predictive model; and
(5) different optimization algorithms may excel at different tasks, determined by the landscapes of oracle functions; which algorithm to select is still dependent on the use case and the type of tasks.