线性回归算法
线性回归算法概述
线性回归是利用数理统计中的回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。线性回归模型是相对简单的回归模型，对一个或多个自变量之间的线性关系进行建模，可用最小二乘法求模型函数。
回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。
线性回归算法计算过程
线性回归算法的目的是来找到一条函数表达式，从而能够最好的拟合给定的数据集。
当得到这条函数表达式的时候，讲所有已知的点代入到这个函数表达式之间，就会得到一个函数值，而这个函数值减去真实值之后就会得到一个误差，将所有的误差平方后求和就是这个函数表达式整体的一个误差，这种将所有误差平方求和的方法叫做残差平方和。得到的结果越大，就说明预测值和实际值差距越大，得到的结果越小，就说明预测值和实际值差距越小，当结果为0时，证明所有的点都在这个函数表达式上。
表达式为
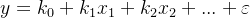
其中
为误差。
举个例子，在二维平面上一些点随机的分布在一条线的两侧，那么线性回归的目的就是找到这条线的函数表达式，得到这条线的函数表达式就能处理未知的点，就能够求出他的结果值。
线性回归算法的使用条件
1.自变量与因变量应该大致呈线性 。
2.残差即真实值与预测值的差的分布为正态分布。
3.残差应该满足方差齐性。
4.自变量之间应是相互独立的，不存在共线性。
正规地来说，应用线性回归分析之前，需要对这四个条件进行检验。如果条件不符合仍然使用线性回归，即使得出结果，精度也会很差。
最小二乘法
最小二乘法公式是一个数学的公式，在数学上称为曲线拟合。
公式为
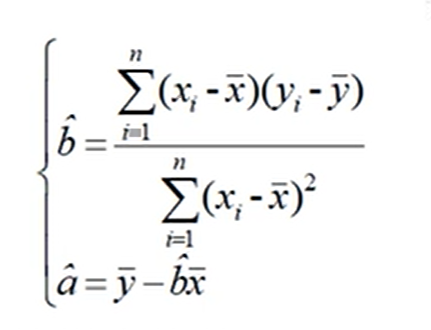
其中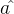
为最小二乘估计的截距，
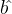为最小二乘估计的斜率，
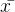和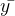
为样本x和y的均值。线性回归算法的函数表达式就是通过最小二乘法所得到的。
线性回归算法的优缺点
优点：
1.运算速度快，由于算法简单，符合非常简洁的数学原理，所以线性回归算法不管时建模速度还是预测速度都是非常快的。
2.可解释性很强，由于最终可以得到一个数学函数表达式，根据计算出的系数就可以明确的知道每个变量的影响大小。
3.善于获取数据集中的线性关系。
缺点：
1.预测的精确度较低，由于获得的模型只是要求最小的损失，而不是数据良好的拟合，所以精确度比较低。
2.不相关的特征会影响结果，对噪声数据处理比较难。
3.不适用于非线性数据。
4.容易出现过拟合，尤其是数据量不大的情况。
线性回归算法代码
from sklearn.linear_model import LinearRegression # 导入线性回归模型
clf = LinearRegression() # 建立线性回归模型对象
clf.fit(x_train, y_train)
res = clf.predict(x_test)代码函数及参数说明见