多目标灰狼优化算法(MGWO)
GWO简介
Mirjalili 等人于2014年提出来的一种群智能优化算法。该算法受到了灰狼捕食猎物活动的启发而开发的一种优化搜索方法,它具有较强的收敛性能、参数少、易实现等特点。
社会等级分层:初始化种群,将适应度最好的三个个体标记为
α
、
β
、
σ
\alpha、\beta、\sigma
α、β、σ,剩下的狼群为
ω
\omega
ω,GWO优化过程中主要由每代种群中三个最好的解来指导完成。
位置更新计算
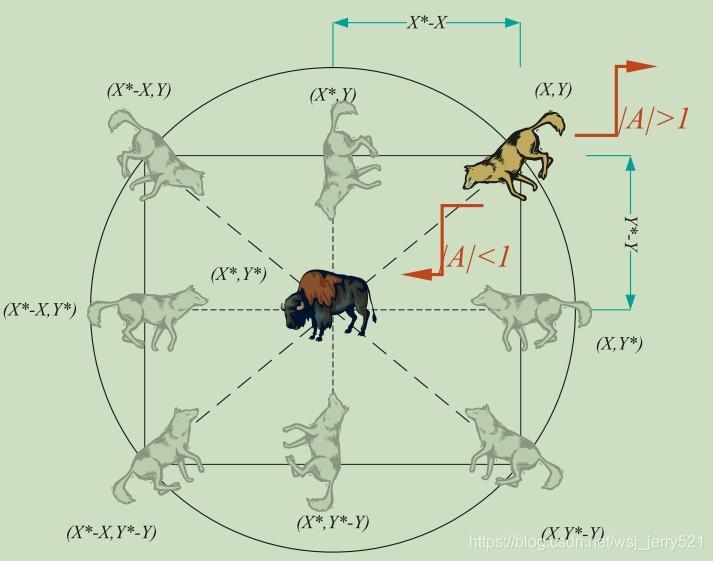 |  |
左边图中表示二维的向量及可能的区域,可以看出灰狼的位置根据中间猎物的位置
(
X
∗
,
Y
∗
)
(X^*,Y^*)
(X∗,Y∗)进行更新,通过调节
A
→
,
C
→
\overrightarrow{A},\overrightarrow{C}
A,C的值,可以到猎物周围不同的地方。
D
→
=
∣
C
→
⋅
X
→
p
(
t
)
−
X
→
(
t
)
∣
A
→
=
2
a
→
⋅
r
1
→
−
α
→
C
→
=
2
⋅
r
2
→
X
→
(
t
+
1
)
=
X
→
p
(
t
)
−
A
→
⋅
D
→
\begin{aligned} &\overrightarrow{D}=\vert \overrightarrow{C}\cdot\overrightarrow{X}_p(t)-\overrightarrow{X}(t)\vert \\ &\overrightarrow{A}=2\overrightarrow{a}\cdot\overrightarrow{r_1}-\overrightarrow{\alpha}\\ &\overrightarrow{C}=2\cdot\overrightarrow{r_2}\\ &\overrightarrow{X}(t+1)=\overrightarrow{X}_p(t)-\overrightarrow{A}\cdot\overrightarrow{D} \end{aligned}
D=∣C⋅Xp(t)−X(t)∣A=2a⋅r1−αC=2⋅r2X(t+1)=Xp(t)−A⋅D
A是[-2,2],随着迭代次数增加线性减少到[-1,1],此时个体还在对猎物进行广泛搜索,当|A|<1时,开始袭击猎物。
r
1
,
r
2
r_1,r_2
r1,r2是[0,1]之间的随机数。种群中所有个体位置更新计算根据上述公式进行计算。
D
→
α
=
∣
C
1
→
⋅
X
→
α
−
X
→
∣
D
→
β
=
∣
C
2
→
⋅
X
→
β
−
X
→
∣
D
→
σ
=
∣
C
3
→
⋅
X
→
σ
−
X
→
∣
X
1
→
=
X
α
→
−
A
1
→
⋅
(
D
α
→
)
X
2
→
=
X
β
→
−
A
2
→
⋅
(
D
β
→
)
X
3
→
=
X
σ
→
−
A
3
→
⋅
(
D
σ
→
)
X
→
(
t
+
1
)
=
X
1
→
+
X
2
→
+
X
3
→
3
\begin{aligned} &\overrightarrow{D}_\alpha=\vert \overrightarrow{C_1}\cdot\overrightarrow{X}_\alpha-\overrightarrow{X}\vert\\ &\overrightarrow{D}_\beta=\vert \overrightarrow{C_2}\cdot\overrightarrow{X}_\beta-\overrightarrow{X}\vert\\ &\overrightarrow{D}_\sigma=\vert \overrightarrow{C_3}\cdot\overrightarrow{X}_\sigma-\overrightarrow{X}\vert\\ &\overrightarrow{X_1}=\overrightarrow{X_\alpha}-\overrightarrow{A_1}\cdot(\overrightarrow{D_\alpha})\\ &\overrightarrow{X_2}=\overrightarrow{X_\beta}-\overrightarrow{A_2}\cdot(\overrightarrow{D_\beta})\\ &\overrightarrow{X_3}=\overrightarrow{X_\sigma}-\overrightarrow{A_3}\cdot(\overrightarrow{D_\sigma})\\ &\overrightarrow{X}(t+1)=\frac{\overrightarrow{X_1}+\overrightarrow{X_2}+\overrightarrow{X_3}}{3} \end{aligned}
Dα=∣C1⋅Xα−X∣Dβ=∣C2⋅Xβ−X∣Dσ=∣C3⋅Xσ−X∣X1=Xα−A1⋅(Dα)X2=Xβ−A2⋅(Dβ)X3=Xσ−A3⋅(Dσ)X(t+1)=3X1+X2+X3
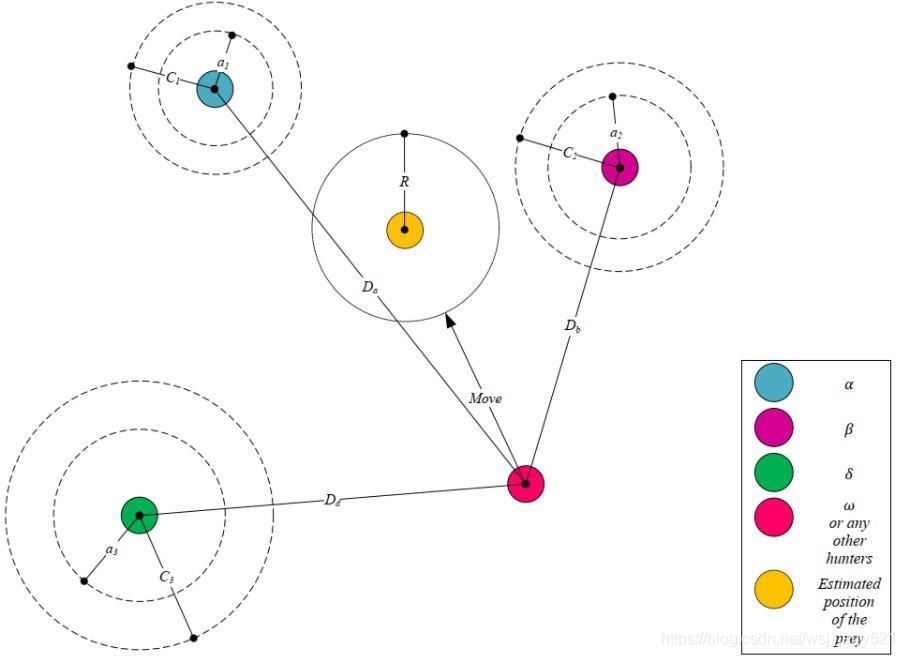
上述公式是根据
α
β
σ
\alpha \beta \sigma
αβσ三只狼来指导狼群中所有狼群位置更新的公式。
MGWO算法流程
Step1:初始化狼群,计算种群中的非支配解集Archive(大小确定),对Archive中的解进行网格计算求网格坐标值。
迭代开始
Step2:从初始Archive中根据网格选择
α
、
β
、
σ
\alpha、\beta、\sigma
α、β、σ,根据三个解进行狼群中所有个体的位置更新。
Step3:全部位置更新之后,计算更新之后种群的非支配解集non_dominates。
Step4:Archive更新—将non_dominates与Archive合并后计算两者的非支配解集,判断是否超过规定的Archive大小,如果超过,根据网格坐标进行删除。
本次迭代结束
Step5:判断是否达到最大迭代次数,是,输出的Archive.否,转Step2.
for it=1:MaxIt
a=2-it*((2)/MaxIt);
for i=1:GreyWolves_num
clear rep2
clear rep3
% Choose the alpha, beta, and delta grey wolves
Delta=SelectLeader(Archive,beta);
Beta=SelectLeader(Archive,beta);
Alpha=SelectLeader(Archive,beta);
% If there are less than three solutions in the least crowded
% hypercube, the second least crowded hypercube is also found
% to choose other leaders from.
if size(Archive,1)>1
counter=0;
for newi=1:size(Archive,1)
if sum(Delta.Position~=Archive(newi).Position)~=0%返回位置不同的个数
counter=counter+1;
rep2(counter,1)=Archive(newi);
end
end
Beta=SelectLeader(rep2,beta);
end
% This scenario is the same if the second least crowded hypercube
% has one solution, so the delta leader should be chosen from the
% third least crowded hypercube.
if size(Archive,1)>2
counter=0;
for newi=1:size(rep2,1)
if sum(Beta.Position~=rep2(newi).Position)~=0
counter=counter+1;
rep3(counter,1)=rep2(newi);
end
end
Alpha=SelectLeader(rep3,beta);
end
% Eq.(3.4) in the paper
c=2.*rand(1, nVar);
% Eq.(3.1) in the paper
D=abs(c.*Delta.Position-GreyWolves(i).Position);
% Eq.(3.3) in the paper
A=2.*a.*rand(1, nVar)-a;
% Eq.(3.8) in the paper
X1=Delta.Position-A.*abs(D);
% Eq.(3.4) in the paper
c=2.*rand(1, nVar);
% Eq.(3.1) in the paper
D=abs(c.*Beta.Position-GreyWolves(i).Position);
% Eq.(3.3) in the paper
A=2.*a.*rand()-a;
% Eq.(3.9) in the paper
X2=Beta.Position-A.*abs(D);
% Eq.(3.4) in the paper
c=2.*rand(1, nVar);
% Eq.(3.1) in the paper
D=abs(c.*Alpha.Position-GreyWolves(i).Position);
% Eq.(3.3) in the paper
A=2.*a.*rand()-a;
% Eq.(3.10) in the paper
X3=Alpha.Position-A.*abs(D);
% Eq.(3.11) in the paper
GreyWolves(i).Position=(X1+X2+X3)./3;
% Boundary checking
GreyWolves(i).Position=min(max(GreyWolves(i).Position,lb),ub);
GreyWolves(i).Cost=fobj(GreyWolves(i).Position')';
end
GreyWolves=DetermineDomination(GreyWolves);
non_dominated_wolves=GetNonDominatedParticles(GreyWolves);
Archive=[Archive
non_dominated_wolves];
Archive=DetermineDomination(Archive);
Archive=GetNonDominatedParticles(Archive);
for i=1:numel(Archive)
[Archive(i).GridIndex Archive(i).GridSubIndex]=GetGridIndex(Archive(i),G);
end
if numel(Archive)>Archive_size
EXTRA=numel(Archive)-Archive_size;
Archive=DeleteFromRep(Archive,EXTRA,gamma);
Archive_costs=GetCosts(Archive);
G=CreateHypercubes(Archive_costs,nGrid,alpha);
end
disp(['In iteration ' num2str(it) ': Number of solutions in the archive = ' num2str(numel(Archive))]);
save results
% Results
costs=GetCosts(GreyWolves);
Archive_costs=GetCosts(Archive);
if drawing_flag==1
hold off
plot(costs(1,:),costs(2,:),'k.');
hold on
plot(Archive_costs(1,:),Archive_costs(2,:),'rd');
legend('Grey wolves','Non-dominated solutions');
drawnow
end
end
相关论文:【Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization】