组合数学
下列所有的符号中,如果没有特殊说明,则n表示集合中所有元素的个数、r表示所取的元素个数,k表示种类数。
第一章:
绪论,介绍了为什么要研究组合数学,以及组合数学的三个研究内容。
第二章:
鸽巢原理:把N+1个鸽子放到N个巢里面,则至少有一个巢里面有两只鸽子。
推论:如果把N个物体放到K个盒子当中,则至少有一个盒子里面有N/k取上界个物体。
例子:Ramsey数
第三章:
1、集合的排列:P(n,r)、集合的循环排列:P(n,r)/r、集合的组合:C(n,r)
2、多重集合的排列:1、每个元素有无限多个,取r个:K^r——有K种元素,也就是说每个位置有K种选择,取r个。
2、每个元素是有限个,全排列数:N!/N1!N2!...Nk!。
3、每个元素是有限个,取r个的排列数:用后面章节的生成函数(指数生成函数)求解
3、多重集合的组合:1、每个元素有无限多个:C(r+k-1,r)
2、每个元素是有限个:用后面章节的容斥原理来求,用容斥原理将有限个转换成无限多个(最多取多少个转换成至少取多少个)。
第四章:
1、活动数:给数标一个方向,如果这个数比他所指方向的那个数大,那么这个数就叫做活动数。
2、生成排列(全排列):活动数法,1、找到一个最大的活动数,2、将这个数与他所指方向的那个数互换位置,3、将所有比他大的数的方向转换。重复这三步,直到所有的数都不是活动数。
3、逆序数:给定一个数的序列,如果Xi>Xj且i<j。则称这两个数为一个逆序对,用ai表示数字i的逆序对的个数,也叫逆序数。
算法1:通过相对位置和从大的数到小的数的逆序数来确定具体序列:i前面有ai个逆序对。
算法2:通过从小的数到大的数逆序数来直接确定具体序列:i直接放在第ai+1个空位上。
4、生成组合:通过2进制的+1来生成所有的组合。
5、生成r-组合:按字典序来排序,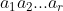 的直接后继是
的直接后继是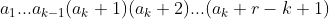 .直接前驱是
.直接前驱是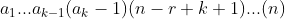 。其中后继的
。其中后继的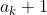 不与原序列任何一个数重复,前驱的
不与原序列任何一个数重复,前驱的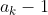 也是如此。
也是如此。
6、生成r-排列:先生成r-组合,然后对每个组合进行全排列。
第六章:
1、容斥原理:S中不具有P1,P2...Pn任何一个属性的元素有如下多个:
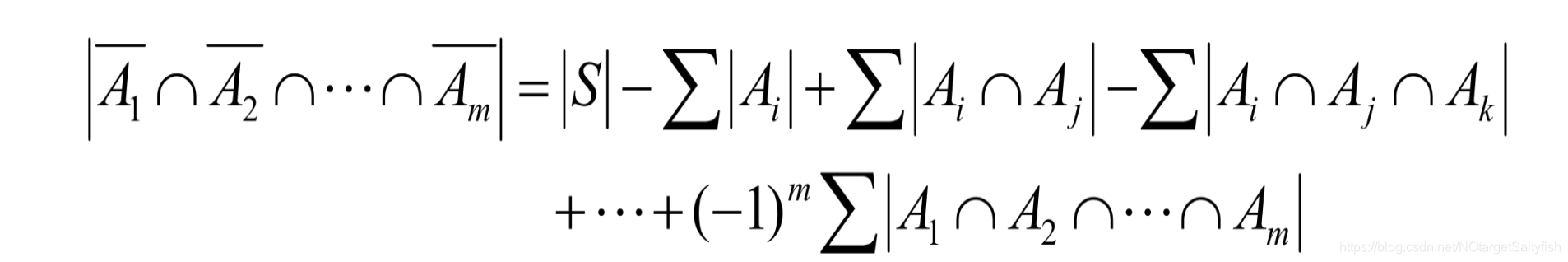
具备任何一种属性中的其中一种的元素有如下多个:
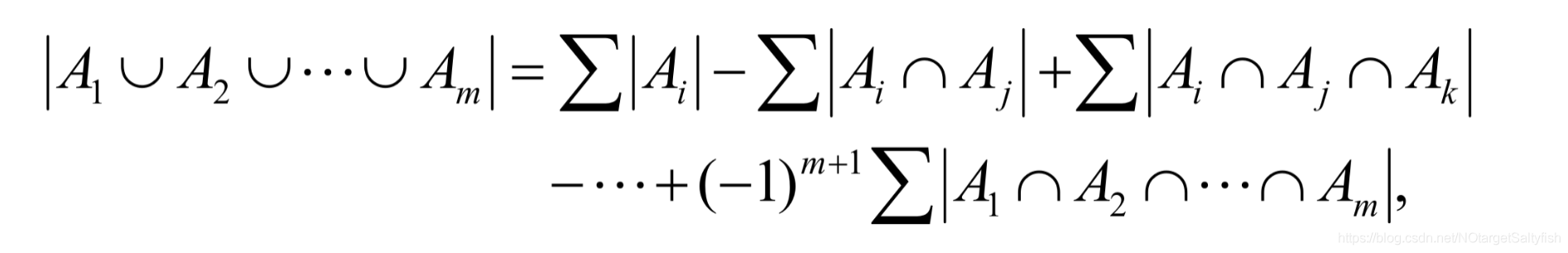
2、错位排列:给定n个数,从1到n,将这n个数排列起来,若任何一个数都不在他的自然位置上,则称这个排列是一个错位排列。例如312,因为1不在第一个位置,2不在第二个位置,3不在第三个位置,所以这是一个错位排列。
我们定义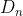 为n个数的错位排列数,则根据容斥原理可得
为n个数的错位排列数,则根据容斥原理可得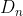 为:
为:
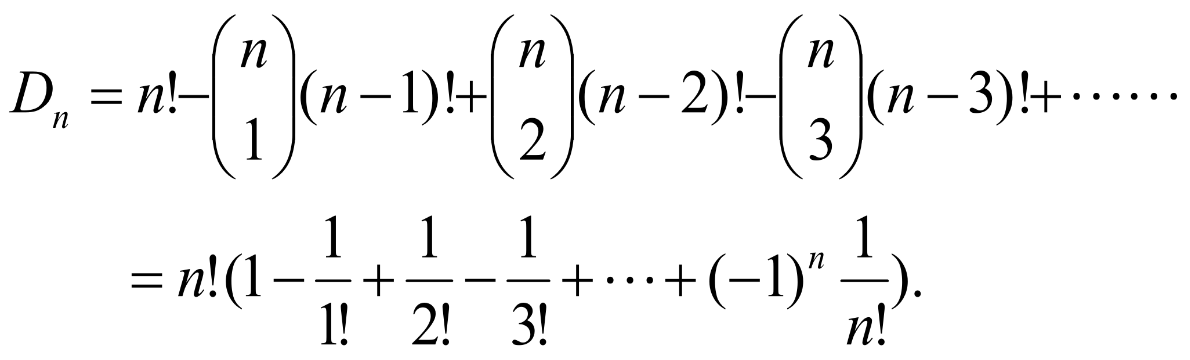
3、带禁止位置的排列:给定N个位置和N个集合,每个位置对应一个集合,带禁止位置的排列就是指,该位置对应的集合中的元素不能在该位置上。当对应的集合中的元素就只有该位置时,带禁止位置的排列就等价于错位排列。
求带禁止位置的排列的时候,当禁止位置的数量不多时,可采用容斥原理来解,但是当禁止位置数量很多时,用容斥原理求解起来很麻烦,因为禁止位置多的时候,求解反问题和原问题复杂度是相同的,因此需要换一种思路来求解这个问题。
4、棋盘多项式:带禁止位置的排列可看成在一个NXN的棋盘上放置N个带禁止位置的非攻击性車(这些車相互之间是有区别的),则在该棋盘上放置N个車的排列数为:
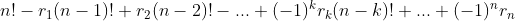
其中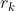 是k个非攻击性車放在相对应的禁止位置上的方法数,现在问题就转换成了如何求解
是k个非攻击性車放在相对应的禁止位置上的方法数,现在问题就转换成了如何求解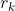 。
。
下面我们用棋盘多项式来求解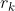 ,
,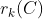 定义在为棋盘C上放K个非攻击性車的方法数。如:
定义在为棋盘C上放K个非攻击性車的方法数。如:
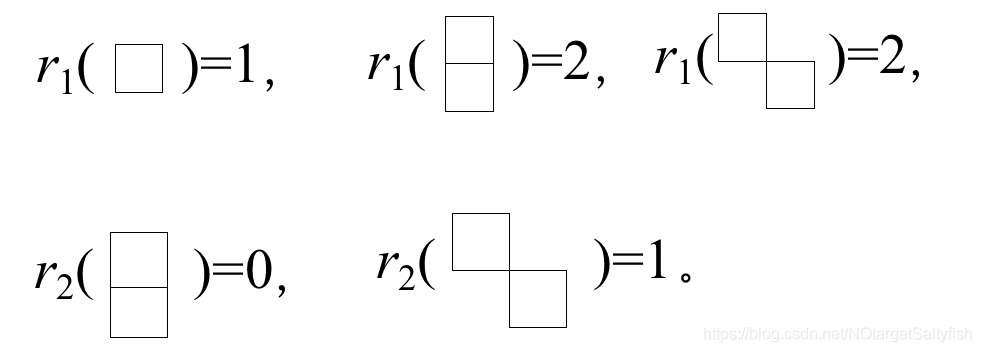
进一步,我们定义:
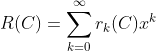 ,
,
其中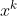 是做位置保持的,对于
是做位置保持的,对于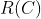 来说,有以下两条性质:
来说,有以下两条性质:
(1) 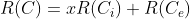 .也就是说,我们可以选定一个方格,然后原棋盘多项式就等于x乘以去掉该方格所在的行和列的棋盘多项式,再加上只去掉这个方格的棋盘多项式,来对一个很大的棋盘进行分解。例如:
.也就是说,我们可以选定一个方格,然后原棋盘多项式就等于x乘以去掉该方格所在的行和列的棋盘多项式,再加上只去掉这个方格的棋盘多项式,来对一个很大的棋盘进行分解。例如:
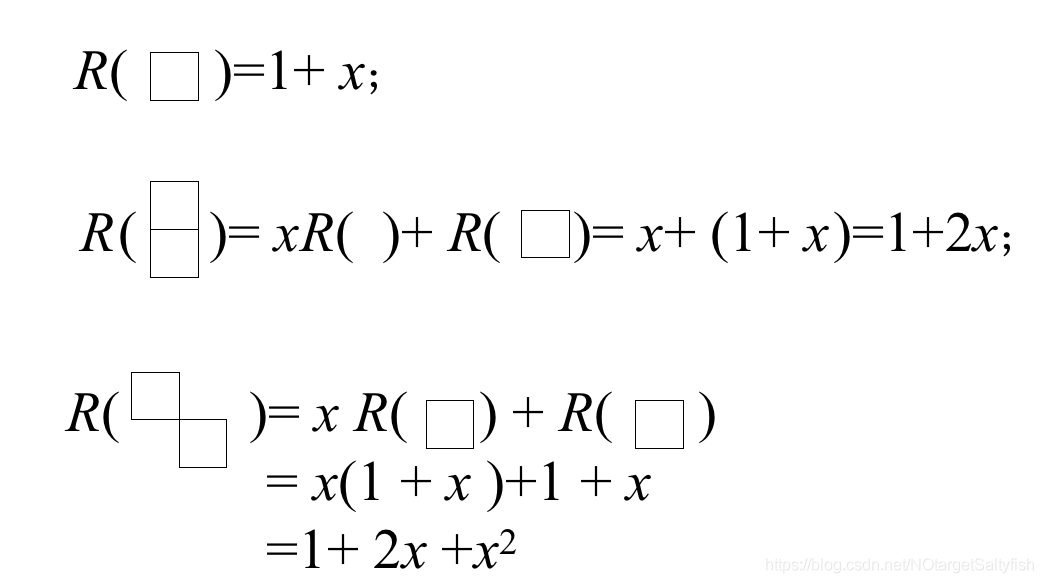
(2)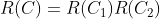 ,其中
,其中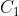 和
和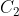 是相互独立的两部分。也就是说,如果一个棋盘可以分解成两个相互独立的部分,则原棋盘多项式就等于这两个独立棋盘多项式的乘积。
是相互独立的两部分。也就是说,如果一个棋盘可以分解成两个相互独立的部分,则原棋盘多项式就等于这两个独立棋盘多项式的乘积。
由以上两条性质,我们可知求解棋盘多项式时,我们应该尽可能挑选那些让棋盘分成两个独立部分的方格,来一步步使原问题变成一个个可直接求解的子问题。例如:
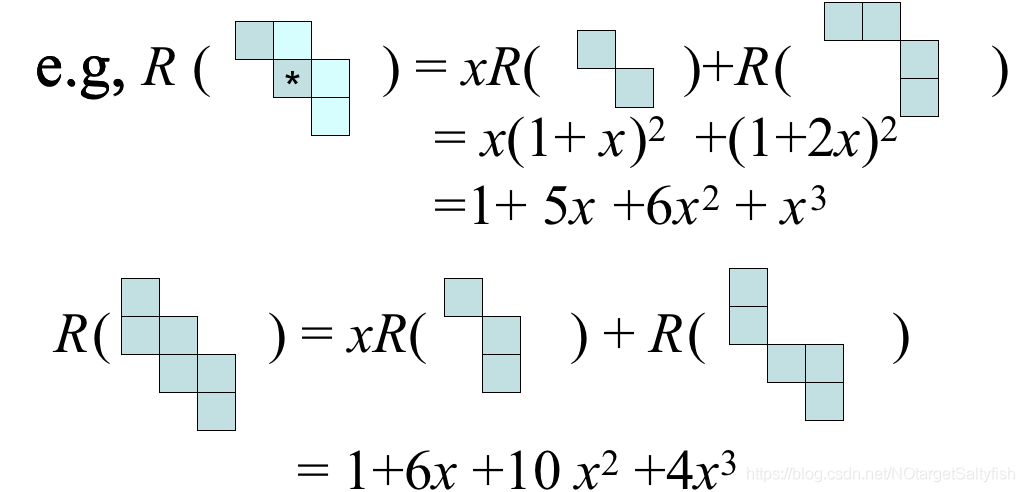
第七章:递推关系式和生成函数
1、线性齐次递推关系式
存在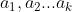 ,
,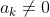 以及
以及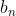 ,使得:
,使得: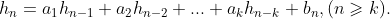 则称这个数列满足K阶线性递推关系式。
则称这个数列满足K阶线性递推关系式。
进一步,如果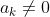 ,
,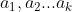 都为常数,且
都为常数,且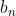 =0,我们称该递推关系式为线性齐次递推关系式。针对线性齐次递推关系式,我们可用以下方法求解:
=0,我们称该递推关系式为线性齐次递推关系式。针对线性齐次递推关系式,我们可用以下方法求解:
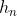 为:
为: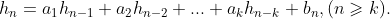
用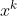 替换
替换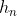 ,
,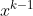 替换
替换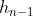 ,依次类推,即得到如下关系式:
,依次类推,即得到如下关系式:
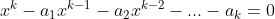
第一种情况:如果该方程有k个互异的根,则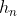 可以表示为:
可以表示为: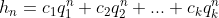 ,为
,为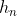 的一般表达式,即非递推表达式。(其中
的一般表达式,即非递推表达式。(其中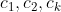 等根据已知的值代入求解)例如:
等根据已知的值代入求解)例如:

代入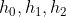 的值即可求出
的值即可求出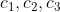 .
.
第二种情况:该方程有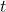 个重根,如果
个重根,如果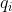 是该方程的
是该方程的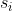 重根,那么
重根,那么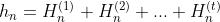 ,其中
,其中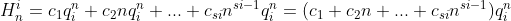 例如:
例如:

2、生成函数:无穷级数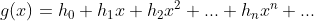 是无穷数列
是无穷数列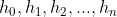 的生成函数,其中
的生成函数,其中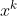 是位置保持,
是位置保持,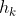 是
是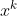 的系数。生成函数的系数即是我们所求解问题的解。
的系数。生成函数的系数即是我们所求解问题的解。

3、用生成函数求解线性齐次递推关系式的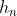 。求解时会用到牛顿二项式定理,先在这里说明一下,
。求解时会用到牛顿二项式定理,先在这里说明一下,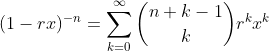
下面给个例子:

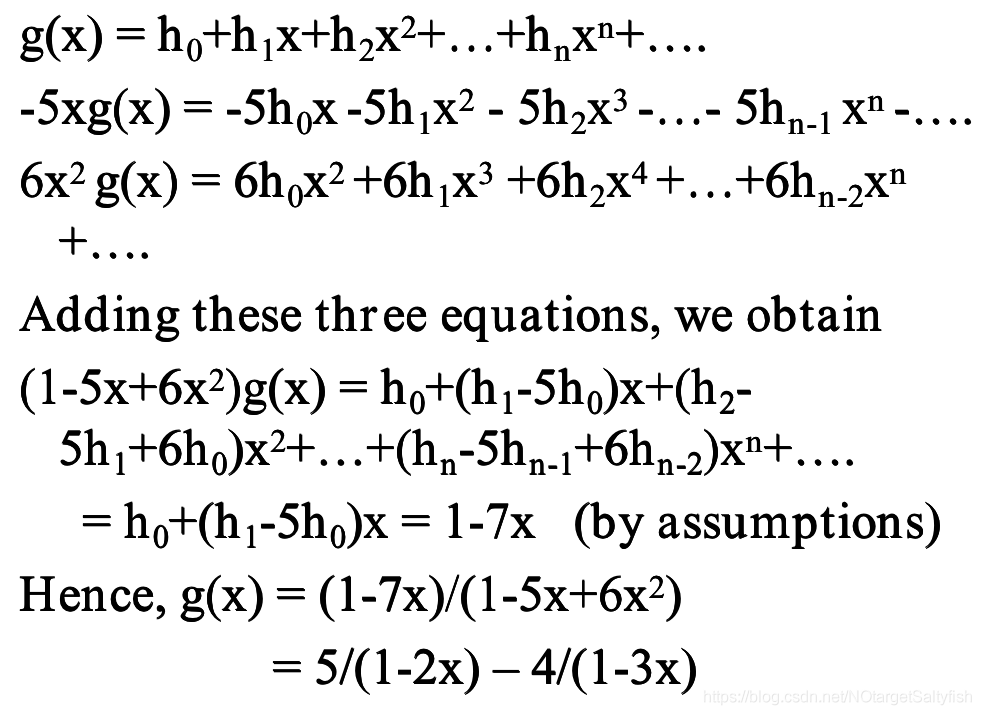

4、一个例子
求凸多边形的三角划分:设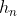 是有n+1条边的凸多边形,则根据该问题可得:
是有n+1条边的凸多边形,则根据该问题可得:
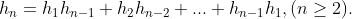
进一步可得: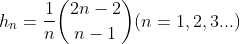 (后面会知道,这是一个特殊计数序列Catalan数)
(后面会知道,这是一个特殊计数序列Catalan数)
5、指数生成函数
将生成函数中的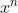 换成
换成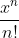 即为指数生成函数,即每一项都除以自身幂次的阶乘,具体的形式为:
即为指数生成函数,即每一项都除以自身幂次的阶乘,具体的形式为:
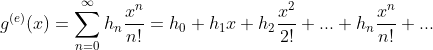
该生成函数用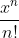 来做位置保持,刚好对应于排列,因此指数生成函数是用来求解排列问题的。
来做位置保持,刚好对应于排列,因此指数生成函数是用来求解排列问题的。
下面给个例子;

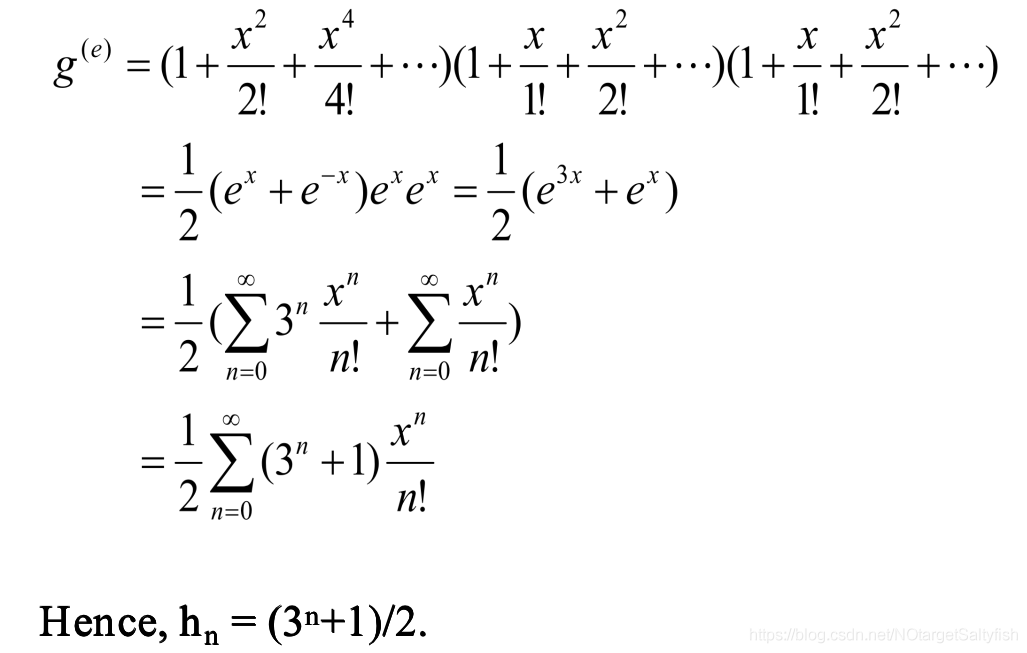
总结:这章介绍了如何用生成函数来求解递归定义的数列,其中生成函数用来求组合问题(与容斥原理不同点在于生成函数通常是求带有要求的无限多个元素的组合问题,例如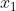 取偶数个,
取偶数个,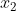 取奇数个),指数生成函数用来求排列问题。
取奇数个),指数生成函数用来求排列问题。
第八章:特殊计数序列
1、Catalan数
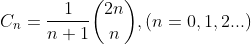
该数的实际意义是:将n个-1和n个1这2n个数排成一个序列,从中任取前k个数,这k个数的和大于等于零的排列数。
2、差分序列
给定一个数的序列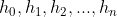 ,差分
,差分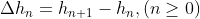 .二阶差分
.二阶差分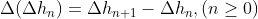 ,依此类推,可以得到三阶差分、四阶差分。这些差分所构成的表称为差分表。且如果
,依此类推,可以得到三阶差分、四阶差分。这些差分所构成的表称为差分表。且如果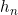 是多项式,则差分表不会无限循环下去,若
是多项式,则差分表不会无限循环下去,若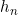 是p阶多项式,则第P+1阶差分一定为0.
是p阶多项式,则第P+1阶差分一定为0.
当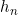 是p阶多项式时,
是p阶多项式时,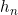 可由差分表的第0条对角线确定。
可由差分表的第0条对角线确定。
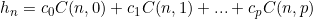 ,其中
,其中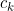 是第0条对角线上的K阶差分。例如:
是第0条对角线上的K阶差分。例如:

且有该序列的前n项和为:
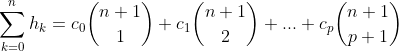
3、Stirling数(这里介绍的是第二类Stirling)
假设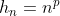 ,差分表的0零对角线上的元素为c(p,0)、c(p,1)、c(p,p),则第二类Stirling数定义为:
,差分表的0零对角线上的元素为c(p,0)、c(p,1)、c(p,p),则第二类Stirling数定义为:
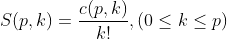
且有: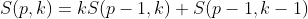
该数的实际意义是把P个物品放到K个不加相互区分的盒子里,且没有哪个盒子是空的,这样的放置的方法数。
如果这些盒子相互区分,那么就有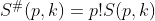 ,即再讲这些盒子全排列。
,即再讲这些盒子全排列。
4、Bell数
Bell数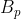 是将p个物品放到非空的相互区分的盒子里的方法数。因此有:
是将p个物品放到非空的相互区分的盒子里的方法数。因此有:
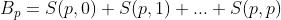
5、划分数
将一个正整数划分成一个或多个正整数的和(划分出来的数相互之间是没有顺序的),这样的划分的种数。定义为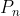 ,
,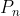 的生成函数为:
的生成函数为:
总结:本章一共介绍了五个特殊计数序列,分别是:(1)Catalan数:把n个-1,n个+1排列起来,且任取前K个,他们的和都不小于零的方法数;(2)第二类Stirling数:将p个元素放到k个不加区分的非空盒子里的方法数;(3)Bell数:将P个元素放到非空盒子里的方法数;(4)第一类Stirling数:把p个元素放到k个非空的循环排列中的方法数;(5)划分数:将一个正整数划分成一个或多个正整数的和的方法数。
第九章:二部图的匹配问题
1、通用问题模型
给定一个二部图G(X,Y, ),对于之前的求非攻击性車的放置数、以及多米诺骨牌的覆盖问题,都可以用二部图的匹配来解。
),对于之前的求非攻击性車的放置数、以及多米诺骨牌的覆盖问题,都可以用二部图的匹配来解。
非攻击性車:X、Y分别是行和列坐标的集合,如果某行某列的位置上可以放置一个非攻击性車,则这两点之间有一条边,那么非攻击性車的放置问题就对应于一个二部图的匹配问题。
多米诺骨牌的覆盖问题:给定一个带禁止位置的棋盘B,求该棋盘的多米诺骨牌覆盖。我们可以通过这种方式来求解此问题,用黑白两色给该棋盘着色,要求为黑色格子的周围是白色格子,白色格子的周围是黑色格子,即相邻两个格子的颜色不能相同,X为黑色格子的集合,Y为白色格子的集合,若这两个格子之间有共同的边,这这两个点之间有一条边。那么多米诺骨牌的覆盖问题也就成了该二部图的匹配问题。
任务分配:X、Y分别是人和任务的集合,如果某一个任务分配给了某个人,则这两者之间有一条边。那么任务分配问题也就成了一个二部图的匹配问题。
由上可见,二部图可用来解很多实际问题,且这些问题都可以转换为二部图的匹配问题,下面介绍二部图的匹配。
2、匹配
极大匹配:不能再加边的匹配。最大匹配:极大匹配中的最大值。
路径:点各不相同的点边序列(除了起始点和结束点可以相同之外),如果起始点和结束点相同,则称之为一个循环。
M渗透点与M非渗透点:给定一个匹配M,如果某一点与该匹配中的边相关联,则称之为M渗透点,如果没有与之关联,则称之为M非渗透点。
M交错路径:给定一个匹配M,M交错路径指的是该路径上的边是前一条在M中,下一条不在M中,依次交替出现的。
M增广路径:起始点和结束点都是M非渗透点的M交错路径。由此可知,M增广路径上不在M中的边的条数比在M中的边的条数多1
有了以上的概念之后,我们对一个增广路径一直增广,即可得到一个最大匹配,其中增广的方法为用该路径上不在M中的边替换该路径上在M中的边,得到一个新的集合M,即M'=(M-Mr)U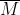 ,M’比M的边数多一。
,M’比M的边数多一。
3、Holl定理
如果存在一个渗透集合X的匹配,当且仅当|N(S)|>=|S|对于所有的S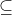 X。即如果一个匹配包括了集合X中的所有点,当且仅当该集合任意子集的邻居节点个数不少于该子集中点的个数。成婚定理也是这个意思。
X。即如果一个匹配包括了集合X中的所有点,当且仅当该集合任意子集的邻居节点个数不少于该子集中点的个数。成婚定理也是这个意思。
完备匹配:包含了二部图中所有的点的匹配叫做一个完备匹配。
K正则图:二部图G中所有点的度数都是K。K正则图一定存在一个完备匹配。
点覆盖:一个点的集合,图G中的任意一条边都能在该集合中找到一个与之关联的点。
最小点覆盖:点覆盖中点数最少的覆盖称为点覆盖。
4、Konig定理:二部图的最小点覆盖数等于最大边匹配数。
5、求最大匹配(最小覆盖)的算法:(1)将所有的M非渗透点标记为*,并且称这些点为未扫描的点(2)对X中所有新标记的点进行扫描,如果不存在新标记的点,则算法停止;否则扫描所有新标记的点,将与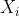 通过不属于M中的边相连的点标记为
通过不属于M中的边相连的点标记为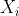 ,扫描完所有新标记的点之后进入下一步(3)如果Y中没有新标记的点,则算法停止,否则扫描Y中所有新标记的点,将与
,扫描完所有新标记的点之后进入下一步(3)如果Y中没有新标记的点,则算法停止,否则扫描Y中所有新标记的点,将与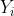 通过在M中的边相连的点标记为
通过在M中的边相连的点标记为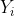 ,扫描完所有的点之后进入步骤(2)。
,扫描完所有的点之后进入步骤(2)。
突破点:Y中存在一个标记了但无法扫描过去的点,这样的点称为突破点。当出现突破点时,可以对该路径进行增广。
非突破点:X中存在一个标记了但无法扫描过去的点,这样的点称为非突破点,当非突破点出现时,该路径为最大匹配。
6、互异代表系统
Y是一个有限集合,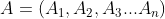 是Y的n个子集族,从每个子集族中找一个元素代表该子集族,如果这n个代表元素互不相同,则称之为一个互异代表系统。
是Y的n个子集族,从每个子集族中找一个元素代表该子集族,如果这n个代表元素互不相同,则称之为一个互异代表系统。
易知,互异代表系统并不总是存在的。当且仅当满足成婚定理时,该子集族有互异代表系统;即从该子集族中任选K个子集族,这K个子集族的并的元素不少于K个时,该子集族存在互异代表系统。
当这N个子集族不存在互异代表系统时,存在互异代表系统的最大子集族的个数可由下列式子中最小的值给出:
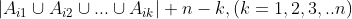
7、稳定婚姻
给定一个优先排名矩阵,使用延迟认可算法可以得到一个稳定婚姻。该算法可分为女士优先和男士优先两种情况,算法步骤为:
(女士优先)只要存在被拒绝的女士,就进行以下操作:
(1)对所有被拒绝的女士来说,找一位排名最高的且没有拒绝她的男士与之匹配。
(2)对每一个男士来说,从选择了他的女士当中挑选一位排名最高的女士延迟认可,拒绝其他所有女士。
第十章:区组设计
1、模运算
给定一个非负整数集合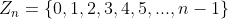 ,定义在该集合上的两个操作,模加和模乘运算。即该集合是一个域,因为模加和模乘这两种操作保证了参与运算的数在经过运算后依然还在这个集合中。
,定义在该集合上的两个操作,模加和模乘运算。即该集合是一个域,因为模加和模乘这两种操作保证了参与运算的数在经过运算后依然还在这个集合中。
定义了模运算及域之后,还需要定义加法逆元和乘法逆元,使得这个运算系统能进行通常的四则运算。
加法逆元:如果a+b=0,则称b是a的加法逆元,反过来,a也是b的加法逆元。
乘法逆元:如果aXb=1,则称b是a的乘法逆元,记做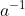 。
。
(此处的加法和乘法都是指的模加和模乘,即定义在该集合上的加法和乘法),易知,并不是域中的所有元素都有乘法逆元,只有当该元素与n互素时才存在乘法逆元。我们可用辗转相除法来求两个数的公因数,当公因数为1时,这两个数互素,我们可以根据该算法得到某个元素的乘法逆元。例如:

2、域及伴随多项式
给定一个素数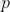 和整数
和整数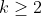 ,我们可以通过添加元素的方法从域
,我们可以通过添加元素的方法从域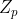 出发构造一个具有
出发构造一个具有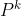 个元素的域,该域中的元素为:
个元素的域,该域中的元素为: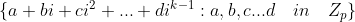 。构造方法为找到一个在
。构造方法为找到一个在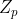 中没有解的
中没有解的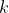 阶多项式,该多项式被称为
阶多项式,该多项式被称为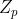 的伴随多项式,该伴随多项式的要求为系数和方程的解都是取自
的伴随多项式,该伴随多项式的要求为系数和方程的解都是取自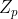 的。然后我们可以通过该多项式和
的。然后我们可以通过该多项式和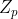 来构造一个新的域,下面给个例子说明这种构造方法:
来构造一个新的域,下面给个例子说明这种构造方法:

3、区组设计
区组设计:给产品分组,但在分组时需要满足某些特定要求。下面给一个例子说明这些特殊要求:

即7种产品分成7组,要求每组中有3个产品,且每一对产品只出现一次,这样要求的分组该怎么设计,即每一组里面是哪几件产品。
模型建立:给定 件产品,
件产品,
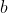 个区组,要求设计一个这样的分组方式:每个区组中有
个区组,要求设计一个这样的分组方式:每个区组中有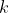 个元素,每个元素出现
个元素,每个元素出现 次,每对元素出现
次,每对元素出现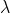 次,
次,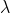 称之为设计指数。当每个区组中包含的元素个数相同时,我们称之为一个平衡区组设计;当k=v时,我们称之为完全区组设计,在这种情况下,每个区组之间是相互独立的,因为每个区组都包含了所有的元素,这种情况在实际中没有研究价值,因此我们研究的都是平衡不完全区组设计,简写为:BIBD,即每个区组中元素个数相同(平衡的),但小于
称之为设计指数。当每个区组中包含的元素个数相同时,我们称之为一个平衡区组设计;当k=v时,我们称之为完全区组设计,在这种情况下,每个区组之间是相互独立的,因为每个区组都包含了所有的元素,这种情况在实际中没有研究价值,因此我们研究的都是平衡不完全区组设计,简写为:BIBD,即每个区组中元素个数相同(平衡的),但小于 (不完全)的区组设计。此外,当
(不完全)的区组设计。此外,当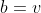 时,称之为对称平衡不完全区组设计,简称:SBIBD.
时,称之为对称平衡不完全区组设计,简称:SBIBD.
BIBD的四条性质:(1)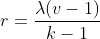 (从元素对的角度)(2)
(从元素对的角度)(2)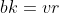 (从单个元素的角度)(3)
(从单个元素的角度)(3)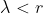 (4)
(4)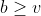
4、区组设计方法
(1)从一个给定的起始区组开始递增,该起始区组需要满足:起始区组中的任意两个元素做差对 取模的值出现的次数相同。即
取模的值出现的次数相同。即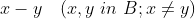 的值出现的次数相同。例如:
的值出现的次数相同。例如:

(2)根据Steiner三元系统来构造一个新的Steiner三元系统。
k=3的平衡区组设计称为Steiner三元系统,如果存在一个元素个数为 和一个元素个数为
和一个元素个数为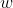 的Steiner三元系统,且设计指数
的Steiner三元系统,且设计指数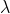 都为1,那么就可以根据这两个三元系统设计一个个数为
都为1,那么就可以根据这两个三元系统设计一个个数为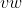 ,
,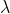 =1的三元系统。如果一个设计指数
=1的三元系统。如果一个设计指数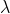 =1的三元系统可以分成几个部分,并且每个部分都包含所有的元素,那么称这个三元系统是可解的,每个部分称之为一个可解类。
=1的三元系统可以分成几个部分,并且每个部分都包含所有的元素,那么称这个三元系统是可解的,每个部分称之为一个可解类。
具体方法为:假设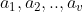 是个数为
是个数为 的三元系统A,
的三元系统A,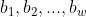 是个数为
是个数为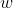 的另一个三元系统B。以A中元素为行,B中元素为列,拼成一个矩阵。
的另一个三元系统B。以A中元素为行,B中元素为列,拼成一个矩阵。
(1)该矩阵中在同一行的且属于B中的某个区组的三个元素构成一个新的区组
(2)该矩阵中在同一列的且属于A中的某个区组的三个元素构成一个新的区组
(3)该矩阵中在不同行和不同列的,且既属于A中的某个区组又属于B中的某个区组的三个元素构成一个新的区组
把符合这三个条件的区组拼起来就可以得到一个个数为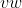 的新的区组。
的新的区组。
(3)根据拉丁方构造区组
拉丁方:拉丁方是集合S上一个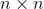 的矩阵,该矩阵每行和每列的元素都取自S,且都各不相同。
的矩阵,该矩阵每行和每列的元素都取自S,且都各不相同。
构造拉丁方:(1)设n是一个正整数,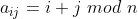 ,这样得到的一个矩阵是一个拉丁方
,这样得到的一个矩阵是一个拉丁方
(2)设n是一个正整数,r是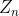 中的一个和n互素的数,
中的一个和n互素的数,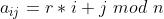 ,这样得到的矩阵也是拉丁方。用这种方法得到的拉丁方我们记为:
,这样得到的矩阵也是拉丁方。用这种方法得到的拉丁方我们记为: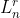
正交拉丁方:如果A、B是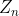 上的两个拉丁方,在并置矩阵AXB中,如果
上的两个拉丁方,在并置矩阵AXB中,如果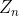 中的每一个序偶(A、B的对应位置拼成一个元组,第一个元素来自A,第二个元素来自B)恰好只出现一次,那么就称这两个拉丁方是正交的,记做MOLS。易知,不存在正交的2阶拉丁方。
中的每一个序偶(A、B的对应位置拼成一个元组,第一个元素来自A,第二个元素来自B)恰好只出现一次,那么就称这两个拉丁方是正交的,记做MOLS。易知,不存在正交的2阶拉丁方。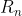 和
和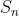 是两个特殊的矩阵:
是两个特殊的矩阵:
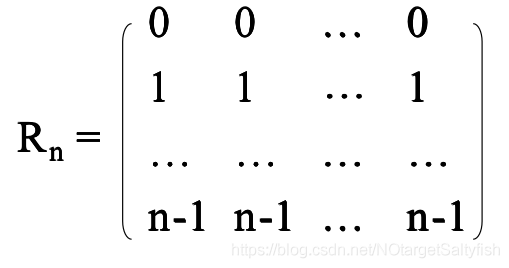
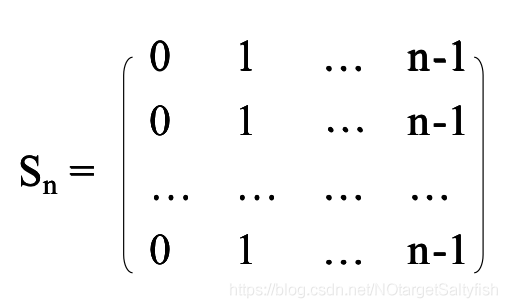
当n是一个素数时,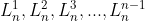 是n-1个n阶MOLS;
是n-1个n阶MOLS;
当n不是一个素数时,我们可以根据之前扩展域的方式来得到n-1个n阶MOLS,设F为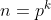 个元素的有限域,p是一个素数,k是一个正整数,假设
个元素的有限域,p是一个素数,k是一个正整数,假设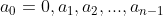 是F中的元素,那么
是F中的元素,那么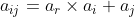 ,这样得到的矩阵是一个拉丁方。且根据这种方法得到的n-1个拉丁方是相互正交的。下面给个例子:
,这样得到的矩阵是一个拉丁方。且根据这种方法得到的n-1个拉丁方是相互正交的。下面给个例子:

构造拉丁方:给定n-1个n阶的互相正交的拉丁方(MOLS),以及上面给的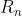 和
和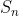 ,我们可以这样构造一个BIBD:
,我们可以这样构造一个BIBD: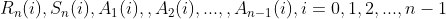 ,这样得到的区组的参数是:
,这样得到的区组的参数是: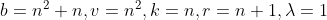 ;反之,如果存在参数形如上式的可解BIBD,则存在n-1个n阶MOLS。
;反之,如果存在参数形如上式的可解BIBD,则存在n-1个n阶MOLS。
下面给个例子:
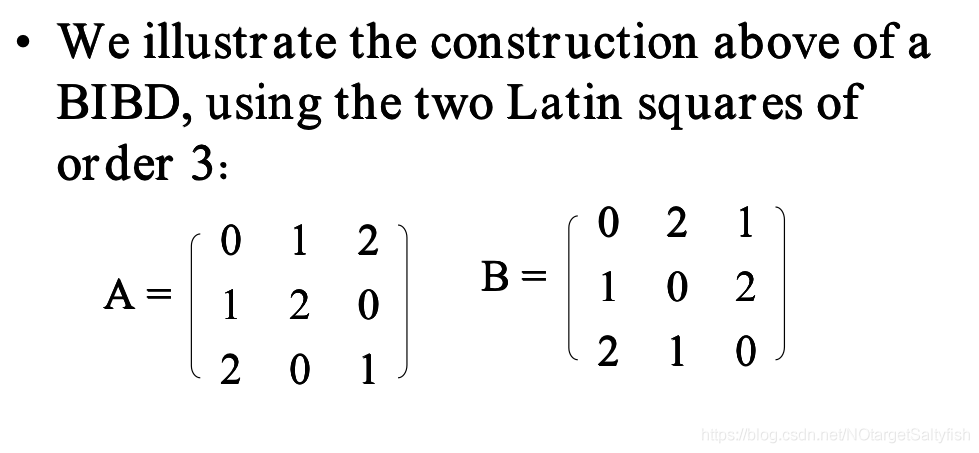

总结:这张介绍了区组设计,以及如何进行区组设计,总共有三种办法,第一种是从一个初始区组开始递增、第二种是用两个Steiner三元系统设计、最后一种是用正交拉丁方。
第14章:Polya计数
1、置换:一种映射,记为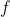 ,将集合
,将集合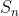 中的数
中的数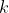 映射到
映射到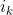 ,该映射是一个满射,集合中所有的点映射完之后还在该集合中。
,该映射是一个满射,集合中所有的点映射完之后还在该集合中。
2、置换群:置换的集合,该集合满足三条性质:1、两个置换的复合还在该集合中。2、一定存在恒等置换3、任一置换有逆置换
3、对称群:集合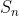 上的所有置换的集合称之为对称群。
上的所有置换的集合称之为对称群。
4、着色方案:C是一个着色方案,C(1)、C(2)、...、C(n)是给n的点着色,着成C(i)的颜色。
5、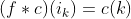 ,该公式的意思是将位置
,该公式的意思是将位置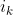 着成
着成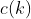 的颜色。即将置换作用在着色方法上,点不变,着色方案按照置换映射到一个新的着色方案。如:
的颜色。即将置换作用在着色方法上,点不变,着色方案按照置换映射到一个新的着色方案。如:
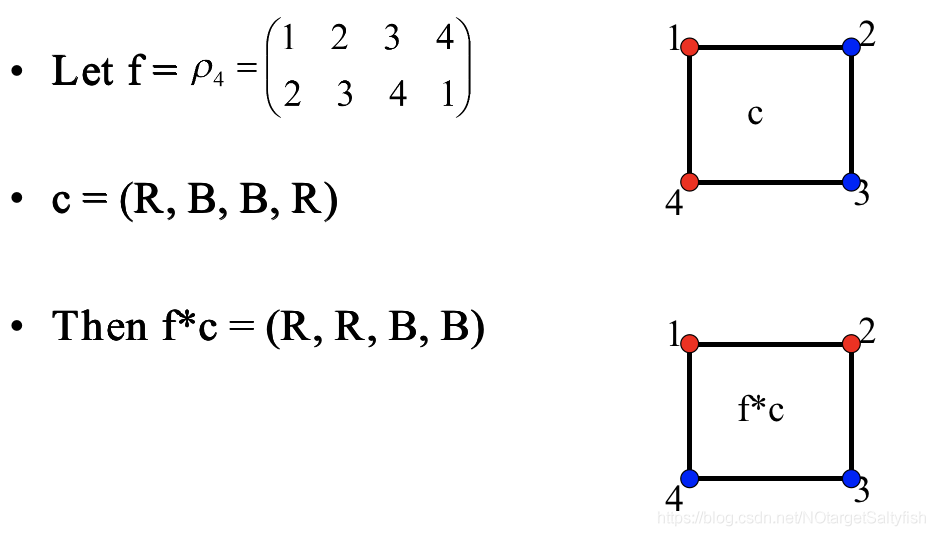
6、等价的着色方案:如果着色方案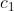 经过某种置换
经过某种置换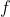 后等于
后等于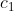 ,那么称这两个置换时等价的,即:如果
,那么称这两个置换时等价的,即:如果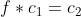 ,那么
,那么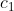 与
与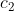 等价.
等价.
7、Burnside定理:我们可以通过这个定理来计算C中的非等价的着色方法数:
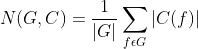
其中N(G,C)表示的是非等价的着色方案数,X是一个集合,如正方形的顶点的集合;G是X的置换群;C是X中满足以下条件的着色集合:对于G中所有的置换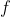 和C中所有的
和C中所有的 都有
都有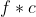 仍然在C中;C(
仍然在C中;C(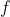 )是在
)是在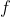 作用下保持不变的着色方案的集合;
作用下保持不变的着色方案的集合;
8、Polya计数
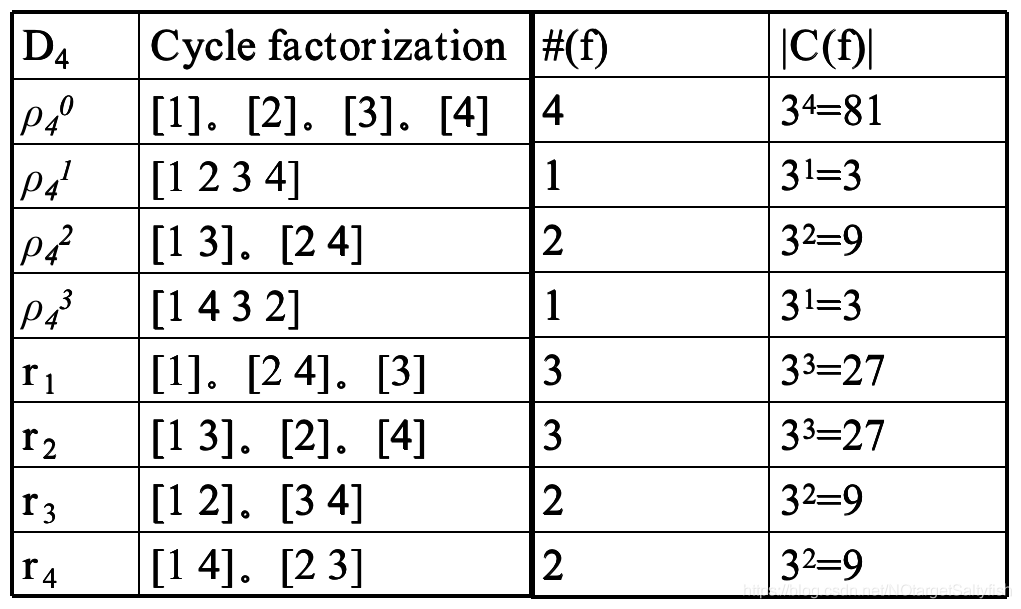
(1)循环因子:置换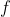 可用几个循环来表示,这些循环被称为循环因子。例如:8阶二面体上的置换群
可用几个循环来表示,这些循环被称为循环因子。例如:8阶二面体上的置换群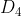
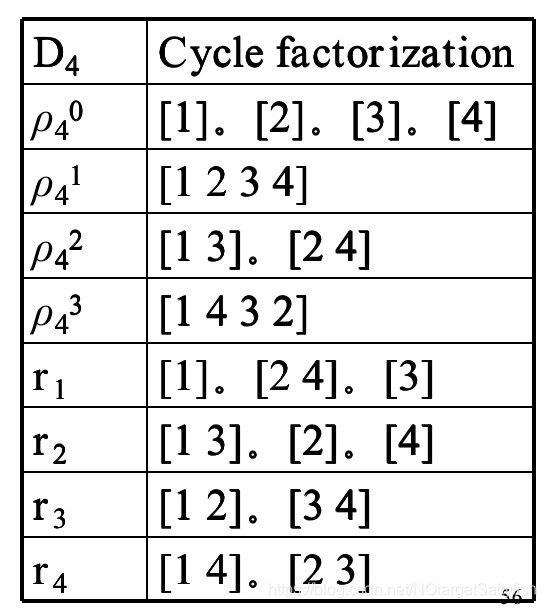
(2)由循环因子可知,对于某个置换来说,只要循环因子的个数确定了,那么不变的着色方案数也就确定了。因为同一个循环因子内的元素必须是同色,否则在经过该置换后着色方案就和之前不等价了。记#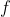 为置换
为置换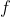 的循环因子数。继续以上述例子为例:
的循环因子数。继续以上述例子为例:
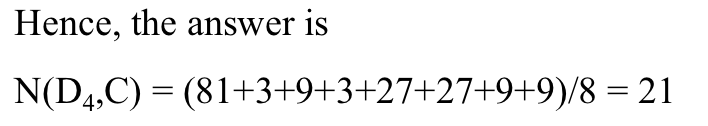
(3)type:我们用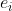 表示元素个数为
表示元素个数为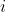 的循环因子个数,那么对于任意一个作用在n个元素上的置换来说,我们可以用元组(
的循环因子个数,那么对于任意一个作用在n个元素上的置换来说,我们可以用元组(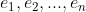 )来表示这个置换的循环因子,因为循环因子里面具体是哪些元素对我们计算
)来表示这个置换的循环因子,因为循环因子里面具体是哪些元素对我们计算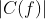 来说没有影响。我们用
来说没有影响。我们用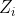 做
做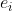 的位置保持,那么就可以得到置换
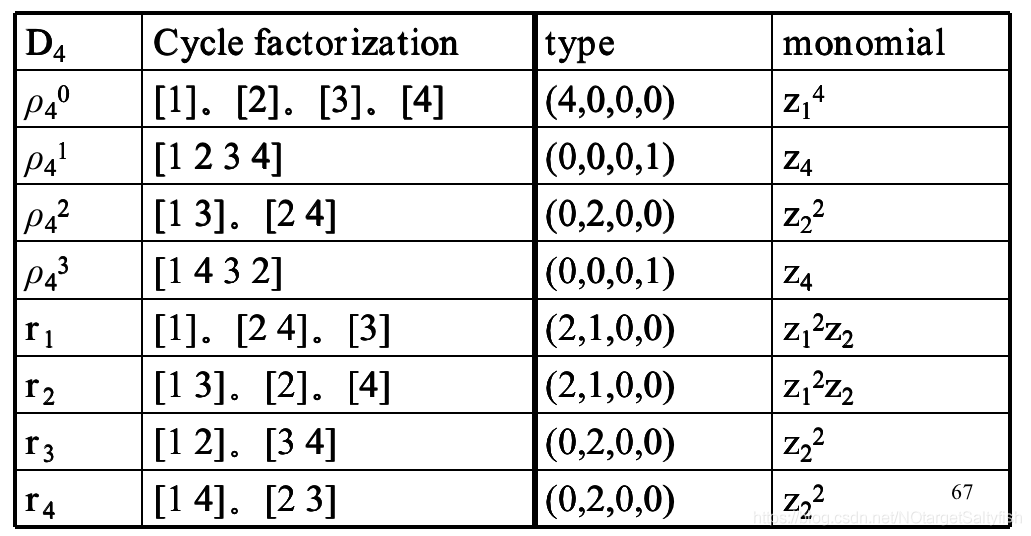
的位置保持,那么就可以得到置换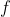 的单项表示,将所有置换的单项表示累加起来除以|G|,就可以得到整个置换的生成函数。还是上面那个例子:
的单项表示,将所有置换的单项表示累加起来除以|G|,就可以得到整个置换的生成函数。还是上面那个例子:
![]()
如果用K种颜色给这个二面体着色,那么非等价的着色方案数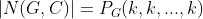 。
。
进一步,如果我们要求一个给特定数量的点着色的方案数,我们只需要用以下方法就可以得到:假设用K种颜色给X中的元素着色,那么生成函数为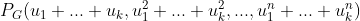 ,即用
,即用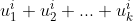 替换
替换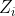 。然后就可以得到给特定数量的点着色的方案数,还是上面那个例子,我们根据这种方法得到的新的生成函数为:
。然后就可以得到给特定数量的点着色的方案数,还是上面那个例子,我们根据这种方法得到的新的生成函数为:
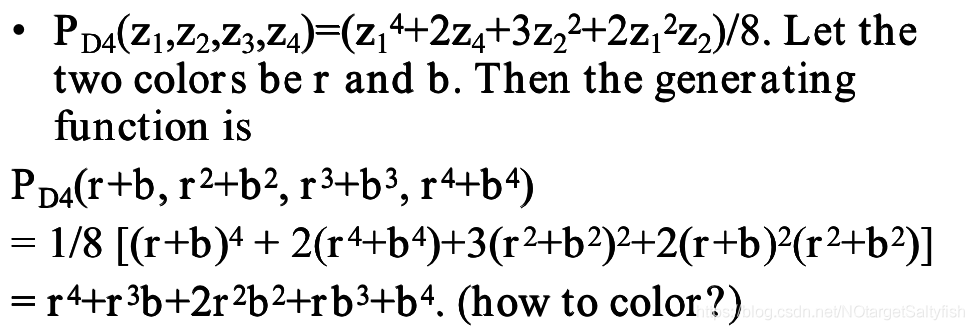
由这个生成可得,如果要两个点红色两个点绿色,那么就是两种。即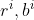 是做未知保持的,幂次指的是用这种颜色着色的点的个数,系数指的是方案数。
是做未知保持的,幂次指的是用这种颜色着色的点的个数,系数指的是方案数。
附:求一个图形对应的循环因子时,如果元素个数是偶数,则在求旋转置换时,会存在某几个点内部构成循环的情况;如果元素个数是奇数,则不存在这种情况,也就是旋转置换只能是所有元素构成一个循环因子,但是如果是偶数则有的情况会有多个循环因子,例如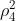 ,有两个元素为2的循环因子。
,有两个元素为2的循环因子。
总结:这章介绍了如何求一个集合上的非等价着色方案数,BurnSide定理给出了求解的具体公式,而polya计数公式则给出了给特定数量的点着特定颜色的具体公式,相当于是Burnside公式的拓展。