三维欧几里德空间中两个向量叉积的问题
定义
两个向量 a和b仅在三维空间中有意义。定义为:
a
⃗
∗
b
⃗
=
∣
∣
a
⃗
∣
∣
∣
∣
b
⃗
∣
∣
s
i
n
θ
\vec{a}*\vec{b}=||\vec{a}||||\vec{b}||sin\theta
a∗b=∣∣a∣∣∣∣b∣∣sinθ
θ
\theta
θ是两向量的夹角。
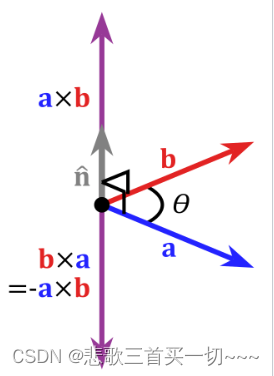
叉积的方向由右手定则确定,模长等于以两个向量为边的平行四边形的面积。
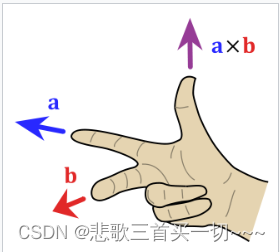
矩阵表示
a
⃗
∗
b
⃗
=
∣
i
⃗
j
⃗
k
⃗
a
1
a
2
a
3
b
1
b
2
b
3
∣
\vec{a}*\vec{b}=\begin{vmatrix} \vec{i}& \vec{j}&\vec{k} \\ a_1& a_2&a_3 \\ b_1&b_2&b_3 \end{vmatrix}
a∗b=
ia1b1ja2b2ka3b3
而向量叉乘可以写为左端向量对应的反对称矩阵与右端向量的乘积形式:
a
∗
b
=
[
a
^
]
b
=
[
0
−
a
3
a
2
a
3
0
−
a
1
−
a
2
a
1
0
]
[
b
1
b
2
b
3
]
\mathbf{a}*\mathbf{b}=[\hat{a}]\mathbf{b}= \begin{bmatrix} 0 & -a_3& a_2 \\ a_3& 0&-a_1\\ -a_2&a_1&0 \end{bmatrix}\begin{bmatrix} b_1 \\ b_2\\ b_3 \end{bmatrix}
a∗b=[a^]b=
0a3−a2−a30a1a2−a10
b1b2b3
几何意义
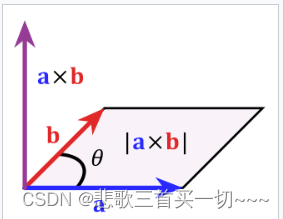
图1:平行四边形面积即外积的模长
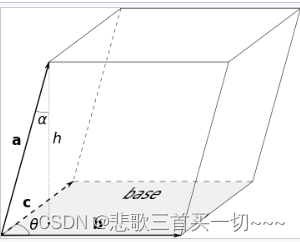
图2:三个向量定义平行六面体
如果以向量
a
⃗
\vec {a}
a和
b
⃗
\vec {b}
b 为边构成一个平行四边形,那么这两个向量外积的模长与这个平行四边形的正面积相等:
a
⃗
∗
b
⃗
=
∣
∣
a
⃗
∣
∣
∣
∣
b
⃗
∣
∣
s
i
n
θ
\vec{a}*\vec{b}=||\vec{a}||||\vec{b}||sin\theta
a∗b=∣∣a∣∣∣∣b∣∣sinθ
同时,如果以向量
a
\mathbf {a}
a 、
b
\mathbf {b}
b 、
c
\mathbf {c}
c 为棱构成一个平行六面体,那么这个平行六面体的体积
V
{\mathbf {V}}
V 也可以通过外积和点积的组合得到,这种积称作标量三重积:
a
⋅
(
b
×
c
)
=
b
⋅
(
c
×
a
)
=
c
⋅
(
a
×
b
)
.
{\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ).}
a⋅(b×c)=b⋅(c×a)=c⋅(a×b).
因为标量三重积可能为负,平行六面体的体积需要取其绝对值:
V
=
∣
a
⋅
(
b
×
c
)
∣
{\displaystyle V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}
V=∣a⋅(b×c)∣
因为外积的模长与其参数夹角的正弦有关,可以认为外积垂直度的度量,正如点积是“平行度”的度量一样。对于任意两个单位向量,外积为1意味着它们互相垂直,外积为0意味着它们互相平行。点积则相反:点积为0意味着它们互相垂直。
单位向量还能带来两个特性:两个单位向量的点积是它们夹角的余弦(可正可负);它们外积的模长则为夹角的正弦(始终为正)。
参考
^Cross Product https://en.wikipedia.org/wiki/Cross_product#Alternative_ways_to_compute_the_cross_product