文章翻译|法线矩阵(The Normal Matrix)
gl_NormalMatrix 存在于很多顶点着色器中,在这里,将会对这个矩阵和他的作用做出解释.本节的灵感来自Eric Lengyel的优秀著作"Mathematics for 3D Game Programming and Computer Graphics".
许多计算都是在眼睛空间完成的,这与光照通常在这个空间中执行有关,否则依赖于眼睛位置的效果,比如镜面光,将更难实现.
因此我们需要一个方式将法线转换到眼部空间.对于顶点到眼睛空间的转换可以使用下面的代码:
vertexEyeSpace = gl_ModelViewMatrix * gl_Vertex;
那么为什么我们不可以直接对于法线向量做相同的计算呢?首先,法线是一个由3个浮点数组成的向量,而模型-视口矩阵是4X4的,其次,由于法线是一个向量,所以我们只想要变换他的方向.模型-视口矩阵中包含旋转功能的部分是左上角3X3的子矩阵,所以为什么不将法线与子矩阵相乘呢?
这很容易用下面的代码实现:
normalEyeSpace = vec3(gl_ModelViewMatrix * vec4(gl_Normal,0.0));
那么,gl_NormalMatrix只是简化代码编写或优化代码的一种快捷方式吗?并不是,上面的代码仅在一些情况下有效.
让我们看一下一种可能的情况:
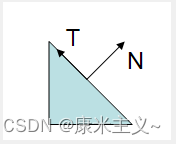
在上面的图中有一个三角形,并标有法线和切线的向量,下面的图片展示当模型-视口矩阵发生不均匀变换时的情况.
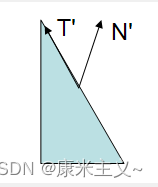
注意:如果缩放是均匀的,那么法线的方向将会被保留,长度将会被改变但可以通过归一化很容易的修复.
在上面的图中,模型-视口矩阵被应用到所有的顶点以及法线上,但结果显然是错误的:被变换后的法线不再垂直于表面.
我们知道,一个向量可以表示为两个点之间的差异,考虑切向量,它可以计算为三角形边的两个顶点之间的差异.如果P1和P2是定义边的顶点,我们知道:
T
=
P
2
−
P
1
T = P_2-P_1
T=P2−P1
考虑到一个向量可以被写成有四个分量的数组,其中最后一个分量是零,我们可以在等式的两侧乘以模型视口矩阵
T ∗ M o d e l v i e w = ( P 2 − P 1 ) ∗ M o d e l v i e w T * Modelview = (P_2-P_1)*Modelview T∗Modelview=(P2−P1)∗Modelview
那么结果就是:
T ∗ M o d e l v i e w = P 2 ∗ M o d e l v i e w − P 1 ∗ M o d e l v i e w T ′ = P 2 ′ − P 1 ′ T*Modelview = P_2*Modelview -P_1*Modelview \\T'=P_2'-P_1' T∗Modelview=P2∗Modelview−P1∗ModelviewT′=P2′−P1′
其中P1’和P2’是变换后三角形的两个顶点,T’代表变换三角形的边的切线,因此,模型视口矩阵保留了切线,但不会保留法线.
考虑用于向量T的方法,我们可以找到两个点Q1和Q2:
N
=
Q
2
−
Q
1
N=Q_2 - Q_1
N=Q2−Q1
主要问题在于,通过变换后的点Q2’,Q1’定义的向量,不一定保持垂直,如上图所示,法向量不是定义为两点之间的差异,就像切向量一样,它被定义为垂直于表面的向量.
所以现在我们知道不可以在任何情况下都使用模型视口矩阵来变换法向量,那下面的问题是应该使用什么矩阵.
考虑一个3X3的矩阵G,然后让我们看看如何计算这个矩阵以正确的变换法向量.
我们知道在矩阵变换之前T·N=0,因为从定义上来说这两个向量相互垂直,我们也知道在变换后T’·N’一定仍然是0,因为他们必须保持垂直, T可以安全的乘以模型视口矩阵左上角3x3的子矩阵(T是一个向量,因此W分量为零),我们称此矩阵为M.
让我们假设矩阵G是用于变换法向量的正确的矩阵,因此有下面的等式:
N
′
⋅
T
′
=
(
G
N
)
⋅
(
M
T
)
=
0
N'·T' = (GN)·(MT) = 0
N′⋅T′=(GN)⋅(MT)=0
点积可以转化为向量的乘积,因此:
(
G
N
)
⋅
(
M
T
)
=
(
G
N
)
T
⋅
(
M
T
)
(GN)·(MT) = (GN)^T·(MT)
(GN)⋅(MT)=(GN)T⋅(MT)
注意,必须考虑第一个向量的转置,因为这是乘以向量所必须的.我们还知道乘法的转置是转置的乘法,因此:
(
G
N
)
T
⋅
(
M
T
)
=
N
T
G
T
M
T
(GN)^T·(MT)=N^TG^TMT
(GN)T⋅(MT)=NTGTMT
我们在开始的时候声明了N和T的点积为0,所以如果:
G
T
M
=
I
G^TM = I
GTM=I
然后还有:
N
′
⋅
T
′
=
N
⋅
T
=
0
N'·T' =N·T=0
N′⋅T′=N⋅T=0
这正是我们想要的,所以我们可以基于M计算G
G
T
M
=
I
G
=
(
M
−
1
)
T
G^TM=I\\G=(M^{-1})^T
GTM=IG=(M−1)T
于是用于变换法线的正确的矩阵就是M矩阵的逆矩阵的转置,OpenGl使用gl_NormalMatrix表示.
在这一节的开始指出在某些情况下使用模型视口矩阵是可行的,每当模型视口矩阵的3X3左上子矩阵是正交的时候我们就有:
M
−
1
=
M
T
G
=
M
M^{-1} = M^T \\G=M
M−1=MTG=M
这是因为在正交矩阵中,转置矩阵与逆矩阵相等。那么,什么是正交矩阵呢?正交矩阵是一个矩阵,其中所有列/行都具有单位长度,并且彼此相互垂直。这意味着当两个向量通过这样一个矩阵相乘时,经过正交矩阵变换后它们之间的夹角与变换之前相同。简单来说,这种变换保持了向量之间的夹角关系,因此变换后的法向量仍然垂直于切向量!此外,它也保持了向量的长度不变。
那么,我们何时可以确信矩阵M是正交的呢?当我们将几何操作限制在旋转和平移上时,即在OpenGL应用中仅使用glRotate和glTranslate而不使用glScale时,可以确保M是正交的。请注意:gluLookAt也创建了一个正交矩阵!