GAMES101：作业3记录

总览

在这次编程任务中，我们会进一步模拟现代图形技术。我们在代码中添加了Object Loader(用于加载三维模型), Vertex Shader 与 Fragment Shader，并且支持了纹理映射。

而在本次实验中，你需要完成的任务是:

• 修改函数 rasterize_triangle(const Triangle& t) in rasterizer.cpp: 在此处实现与作业 2 类似的插值算法，实现法向量、颜色、纹理颜色的插值。
• 修改函数 get_projection_matrix() in main.cpp: 将你自己在之前的实验中实现的投影矩阵填到此处，此时你可以运行 ./Rasterizer output.png normal来观察法向量实现结果。
• 修改函数 phong_fragment_shader() in main.cpp: 实现 Blinn-Phong 模型计算 Fragment Color.
• 修改函数 texture_fragment_shader() in main.cpp: 在实现 Blinn-Phong的基础上，将纹理颜色视为公式中的 kd，实现 TextureShading Fragment Shader.
• 修改函数 bump_fragment_shader() in main.cpp: 在实现 Blinn-Phong 的基础上，仔细阅读该函数中的注释，实现 Bump mapping.
• 修改函数 displacement_fragment_shader() in main.cpp: 在实现 Bump mapping 的基础上，实现 displacement mapping
  这将会生成命名为 Rasterizer 的可执行文件。使用该可执行文件时，你传入的第二个参数将会是生成的图片文件名，而第三个参数可以是如下内容：

使用

texture: 使用代码中的 texture shader.
使用举例: ./Rasterizer output.png texture
normal: 使用代码中的 normal shader.
使用举例: ./Rasterizer output.png normal
phong: 使用代码中的 blinn-phong shader.
使用举例: ./Rasterizer output.png phong
bump: 使用代码中的 bump shader.
使用举例: ./Rasterizer output.png bump
displacement: 使用代码中的 displacement shader.
使用举例: ./Rasterizer output.png displacement
当你修改代码之后，你需要重新 make 才能看到新的结果。

框架代码说明

相比上次实验，我们对框架进行了如下修改：

• 我们引入了一个第三方.obj 文件加载库来读取更加复杂的模型文件，这部分库文件在OBJ_Loader.h file. 你无需详细理解它的工作原理，只需知道这个库将会传递给我们一个被命名被 TriangleList 的 Vector，其中每个三角形都有对应的点法向量与纹理坐标。此外，与模型相关的纹理也将被一同加载。
  注意：如果你想尝试加载其他模型，你目前只能手动修改模型路径。
• 我们引入了一个新的 Texture 类以从图片生成纹理，并且提供了查找纹理颜色的接口：Vector3f getColor(float u, float v)
• 我们创建了 Shader.hpp 头文件并定义 fragment_shader_payload，其中包括了 Fragment Shader 可能用到的参数。目前 main.cpp 中有三个 Fragment Shader，其中 fragment_shader 是按照法向量上色的样例 Shader，其余两个将由你来实现。
• 主渲染流水线开始于 rasterizer::draw(std::vector<Triangle> &TriangleList).我们再次进行一系列变换，这些变换一般由 Vertex Shader 完成。在此之后，我们调用函数 rasterize_triangle.
• rasterize_triangle 函数与你在作业 2 中实现的内容相似。不同之处在于被设定的数值将不再是常数，而是按照 Barycentric Coordinates 对法向量、颜色、纹理颜色与底纹颜色 (Shading Colors) 进行插值。回忆我们上次为了计算z value 而提供的 [alpha, beta, gamma]，这次你将需要将其应用在其他参数的插值上。你需要做的是计算插值后的颜色，并将 Fragment Shader 计算得到的颜色写入 framebuffer，这要求你首先使用插值得到的结果设置 fragment shader payload，并调用 fragment shader 得到计算结果。

运行与结果

在你按照上述说明将上次作业的代码复制到对应位置，并作出相应修改之后（请务必认真阅读说明），你就可以运行默认的 normal shader 并观察到如下结果：

实现 Blinn-Phong 反射模型之后的结果应该是：

实现纹理之后的结果应该是：

实现 Bump Mapping 后，你将看到可视化的凹凸向量:

实现 Displacement Mapping 后，你将看到如下结果:

---

代码实现

我们先看一下rasterizer::draw的实现：

void rst::rasterizer::draw(std::vector<Triangle *> &TriangleList) {

    float f1 = (50 - 0.1) / 2.0;
    float f2 = (50 + 0.1) / 2.0;

    Eigen::Matrix4f mvp = projection * view * model;
    for (const auto& t:TriangleList)
    {
        Triangle newtri = *t;

        std::array<Eigen::Vector4f, 3> mm {
                (view * model * t->v[0]),
                (view * model * t->v[1]),
                (view * model * t->v[2])
        };//得到相机下的四维坐标
        

        std::array<Eigen::Vector3f, 3> viewspace_pos;
        std::transform(mm.begin(), mm.end(), viewspace_pos.begin(), [](auto& v) {
            return v.template head<3>();
        });//得到相机下的三维坐标
 
        Eigen::Vector4f v[] = {
                mvp * t->v[0],
                mvp * t->v[1],
                mvp * t->v[2]
        };//计算屏幕坐标

        //Homogeneous division
        for (auto& vec : v) {
            vec.x()/=vec.w();
            vec.y()/=vec.w();
            vec.z()/=vec.w();           
        }//进行了齐次除法，也就是透视除法，视锥体被变换到一个立方体


        Eigen::Matrix4f inv_trans = (view * model).inverse().transpose();
        Eigen::Vector4f n[] = {
                inv_trans * to_vec4(t->normal[0], 0.0f),
                inv_trans * to_vec4(t->normal[1], 0.0f),
                inv_trans * to_vec4(t->normal[2], 0.0f)
        };//计算变换以后得新法线的方向

        //Viewport transformation
        for (auto & vert : v)
        {
            vert.x() = 0.5*width*(vert.x()+1.0);
            vert.y() = 0.5*height*(vert.y()+1.0);
            vert.z() = -vert.z() * f1 + f2;//这里要添加一个负号
        }

        for (int i = 0; i < 3; ++i)
        {
            //screen space coordinates
            newtri.setVertex(i, v[i]);
        }

        for (int i = 0; i < 3; ++i)
        {
            //view space normal
            newtri.setNormal(i, n[i].head<3>());
        }

        newtri.setColor(0, 148,121.0,92.0);
        newtri.setColor(1, 148,121.0,92.0);
        newtri.setColor(2, 148,121.0,92.0);

        // Also pass view space vertice position
        rasterize_triangle(newtri, viewspace_pos);
    }
}

① 经过MV变换我们得到view space的点，存在mm里，而后传递给viewspace_pos，后面传递给了rasterize_triangle函数作为着色点的位置用于计算光源到着色点的单位向量。
② 经过MVP变换我们得到投影空间的点，这时候已经投影到了平面，不过这时候投影的原点在矩形的中心，保存在了v，然后对这个齐次坐标进行了齐次除法（x,y,z分量除以第四个分量）w坐标记录了原本的z值，但是后面似乎没有用到。
③ MV变换后的点法向量和原来的法向量不同，中间差了一个矩阵: $(MV{)}^{-T}$，这个推导在这篇文章里有写：计算机图形学五：局部光照模型(Blinn-Phong 反射模型)与着色方法(Phong Shading)
④ 为了变换到当前的屏幕的空间（原点在左下角，x轴向右，y轴向上），再次对MVP变换后的点做了一次变换：

for (auto & vert : v)
{
    vert.x() = 0.5*width*(vert.x()+1.0);
    vert.y() = 0.5*height*(vert.y()+1.0);
    vert.z() = -vert.z() * f1 + f2;//这里要添加一个负号
}

下面是从论坛截的一些同学的评论，觉得也挺好。作业3 interpolated_shadingcoords

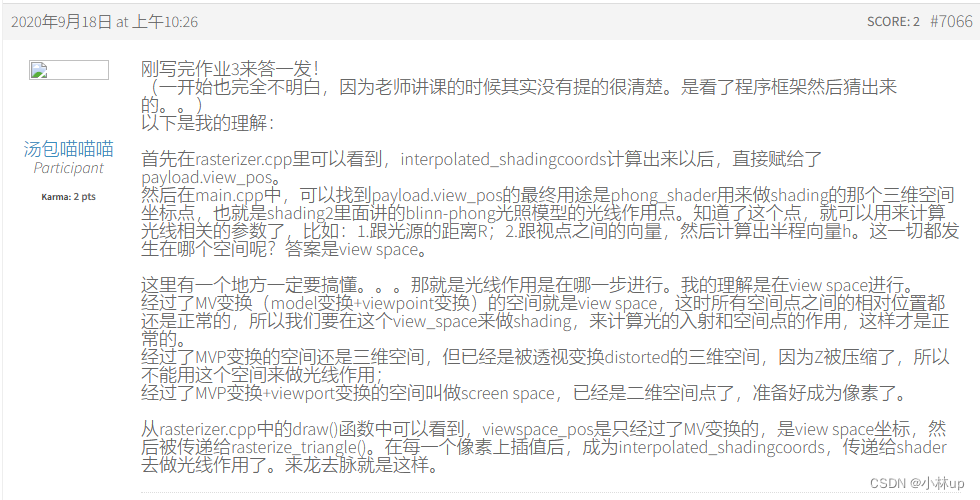
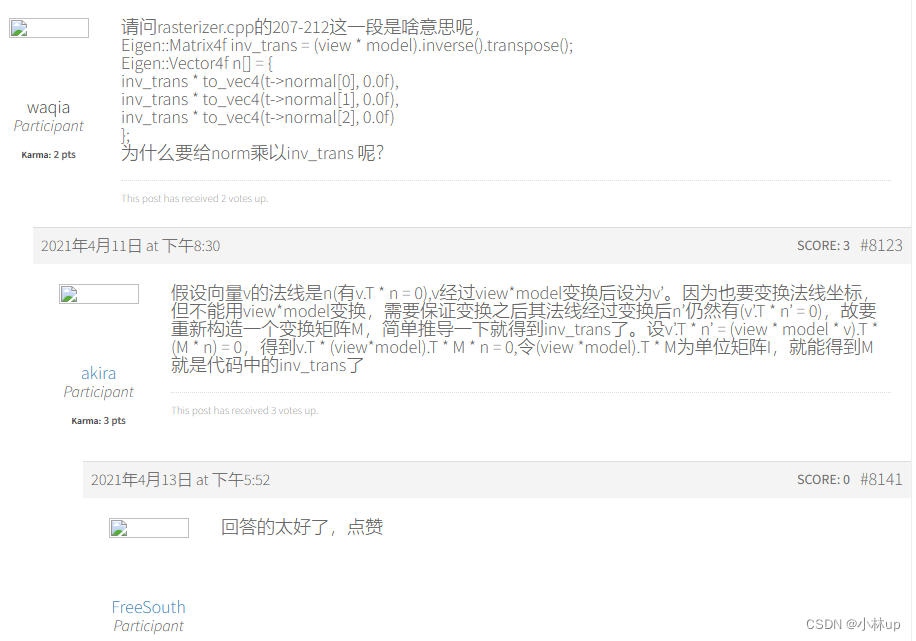
总结：在rasterizer::draw()函数里，使用newtri记录三角形的指针，并重新定义了三角形的属性：①法线：在相机空间viewspace（只进行MV变换）通过setNormal()函数实现;②顶点位置：在screen space(屏幕空间)，通过setVertex()函数实现，③viewspace下的三角形顶点的坐标通过参数的形式传递给了rasterize_triangle()函数，用作viewspace下使用重心插值公式渲染像素点的坐标interpolated_shadingcoords（详情看rasterize_triangle()函数）

rasterize_triangle(const Triangle& t)的实现

void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos) 
{
    // TODO: From your HW3, get the triangle rasterization code.
    // TODO: Inside your rasterization loop:
    //    * v[i].w() is the vertex view space depth value z. //顶点的深度值
    //    * Z is interpolated view space depth for the current pixel //当前像素的坐标值的深度
    //    * zp is depth between zNear and zFar, used for z-buffer//zp计算的像素在zNear和zFar之间的深度，使用在z-buffer算法里
    
    // float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());//alpha beta gamma通过插值函数求出
    // float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
    // zp *= Z;

    //view_pos: 这里使用的是相机下看到的坐标

    // TODO: Interpolate the attributes:
    // auto interpolated_color
    // auto interpolated_normal
    // auto interpolated_texcoords
    // auto interpolated_shadingcoords

    // Use: fragment_shader_payload payload( interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
    // Use: payload.view_pos = interpolated_shadingcoords;
    // Use: Instead of passing the triangle's color directly to the frame buffer, pass the color to the shaders first to get the final color;
    // Use: auto pixel_color = fragment_shader(payload);

    auto v = t.toVector4();

       
    // TODO : Find out the bounding box of current triangle.
    int bounding_box_left_x = std::min(v[0].x(), std::min(v[1].x(), v[2].x()));
    int bounding_box_right_x = std::max(v[0].x(), std::max(v[1].x(), v[2].x()));
    int bounding_box_bottom_y = std::min(v[0].y(), std::min(v[1].y(), v[2].y()));
    int bounding_box_top_y = std::max(v[0].y(), std::max(v[1].y(), v[2].y()));
    for (int x = bounding_box_left_x; x <= bounding_box_right_x; x++) {
        for (int y = bounding_box_bottom_y; y <= bounding_box_top_y; y++) {
            if (insideTriangle(x + 0.5, y + 0.5, t.v)) {
                // If so, use the following code to get the interpolated z value.   
                auto[alpha, beta, gamma] = computeBarycentric2D(x + 0.5, y + 0.5, t.v);
                float Z = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());

                // 计算正确的深度值
                float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                zp *= Z; //zp是正确的深度值
                if (zp <  depth_buf[get_index(x, y)]) {
                    depth_buf[get_index(x, y)] = zp;
                    
                    //auto interpolated_color
                    auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1.0);
                    auto interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1.0);
                    auto interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1.0);
                    auto interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1.0);
                    fragment_shader_payload payload( interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
                    payload.view_pos = interpolated_shadingcoords;
                    auto pixel_color = fragment_shader(payload);
                    set_pixel(Eigen::Vector2i(x, y),  pixel_color);
                }
            }
        }
    } 
} 

这里使用toVector4函数将t的w值全部变为了1，这里本来需要存储深度值的，但是这几行代码还是把z的值求出来了（范围在0.1到50）：

auto[alpha, beta, gamma] = computeBarycentric2D(x + 0.5, y + 0.5, t.v);
float Z =1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
// 计算正确的深度值
float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
zp *= Z; //zp是正确的深度值

首先这里使用了computeBarycentric2D进行插值，这里使用了二维点来插值得到了在view平面上的alpha,beta和gamma，这里使用了平面的重心坐标公式，这里直接给出可以和上面的代码比较（具体可以到computeBarycentric2D这个函数下面查看）：

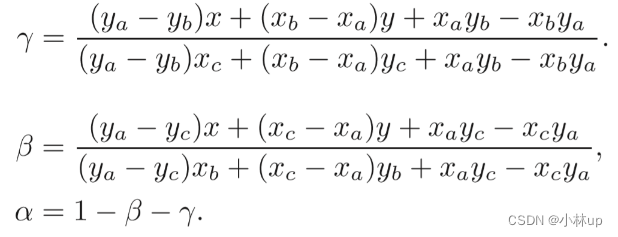
具体可以查看这几篇文章：

计算机图形学三(补充)：重心坐标(barycentric coordinates)详解及其作用
Perspective Correct Interpolation

但是这肯定是有误差的，我们希望的还是在真实的三维空间找到它的深度，这时候就需要用到透视校正插值了，这里给出透视校正插值的公式，具体可以看这篇文章的推导了解透视校正插值：【重心坐标插值、透视矫正插值】原理以及用法见解(GAMES101深度测试部分讨论)

$$Z_t=\frac{1}{\frac{\alpha }{Z_A}+\frac{\beta }{Z_B}+\frac{\gamma }{Z_C}}=1$$

由于使用的三角形在toVector4函数的作用下三个顶点的深度都变为1，所以这里等价于：

$$Z_t=\frac{1}{\alpha +\beta +\gamma }=1$$

然后计算真实的深度（后面两行的代码）

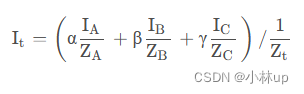
$$zp=(\alpha \frac{z_0}{1}+\beta \frac{z_1}{1}+\gamma \frac{z_2}{1})=\alpha z_0+\beta z_1+\gamma z_2$$

依然计算出了0.1到50 的深度（但我觉得这个深度不是真正的深度，真正的深度应该和摄像机的位置有关？不过下面的计算不影响，我们只是用这个“深度”判断是否更靠近相机）。

关于透视校正插值可以看这篇文章：

计算机图形学六：正确使用重心坐标插值(透视矫正插值(Perspective-Correct Interpolation))和图形渲染管线总结

注意这一句：

set_pixel(Eigen::Vector2i(x, y),  pixel_color);

和之前的渲染三角形不一样，参数列表的第一个参数是Eigen::Vector2i类型的，我复制作业2的代码提示数组的维度不一样报错了，原来的是Eigen::Vector3f的类型。

另外和作业2一样，insideTriangle函数的参数列表里的x和y我们还是使用了float类型，因为我们在rasterize_triangle(const Triangle& t)中使用了x+0.5和y+0.5作为这个函数的第一和第二个参数（像素的中心）。

static bool insideTriangle(float x, float y, const Vector4f* _v){// 这里还是一样进行了参数列表的修改
    Vector3f v[3];
    for(int i=0;i<3;i++)
        v[i] = {_v[i].x(),_v[i].y(), 1.0};
    Vector3f f0,f1,f2;
    f0 = v[1].cross(v[0]);
    f1 = v[2].cross(v[1]);
    f2 = v[0].cross(v[2]);
    Vector3f p(x,y,1.);
    if((p.dot(f0)*f0.dot(v[2])>0) && (p.dot(f1)*f1.dot(v[0])>0) && (p.dot(f2)*f2.dot(v[1])>0))
        return true;
    return false;
}

get_projection_matrix()的实现

首先在main.cpp插入我们之前写的投影矩阵的代码，直接复制以前的就好：

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
{
    // TODO: Use the same projection matrix from the previous assignments
    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    float t = abs(zNear) * tan(eye_fov * MY_PI / (180 * 2));
    float r = aspect_ratio * t;
    float l = -r;
    float b = -t;
    float n = -zNear;
    float f = -zFar;
    projection(0, 0) = 2 * n / (r - l);
    projection(0, 2) = (l + r) / (l - r);
    projection(1, 1) = 2 * n / (t - b);
    projection(1, 2) = (b + t) / (b - t);
    projection(2, 2) = (f + n) / (n - f);
    projection(2, 3) = 2 * f * n / (f - n);
    projection(3, 2) = 1.0;
    projection(3, 3) = 0.0;

    return projection;

}

为了不让我们的图形覆盖的顺序颠倒，我们需要修改rasterizer.cpp中的void rst::rasterizer::draw(std::vector<Triangle *> &TriangleList)

找到这一行：

vert.z() = vert.z() * f1 + f2;

右边的vert.z()前面添加一个负号

vert.z() = -vert.z() * f1 + f2;

否则可能会出现和之前一样的牛牛的屁屁对着我们的情况（三角形的覆盖是顺序有问题，这里是左右手系对应的问题，因为我的投影矩阵使用的还是右手系也就是闫老师说的那个矩阵，但是框架代码使用的是左手系，需要颠倒一下）。

我们编译，在命令行输入命令

./Rasterizer output.png normal

可以得到：

我们看下纹理映射实现的源码：

Eigen::Vector3f normal_fragment_shader(const fragment_shader_payload& payload)
{
    Eigen::Vector3f return_color = (payload.normal.head<3>().normalized() + Eigen::Vector3f(1.0f, 1.0f, 1.0f)) / 2.f;
    Eigen::Vector3f result;
    result << return_color.x() * 255, return_color.y() * 255, return_color.z() * 255;
    return result;
}

因为发现的方向的三个分量的范围是[-1,1]，我们加上1就变为[0,2]，再除以2就归一化为[0,1]，也就变成了RGB三个颜色分量的范围。

phong_fragment_shader()的实现

使用Phong Shading，详细可以参考计算机图形学五：局部光照模型(Blinn-Phong 反射模型)与着色方法(Phong Shading)，公式如下：

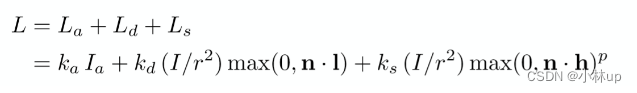
这里根据公式写代码即可：

Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = payload.color;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = payload.color;
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    Eigen::Vector3f result_color = {0, 0, 0};

    for (auto& light : lights)
    {
        // TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular* 
        Eigen::Vector3f r = light.position - point;
        Eigen::Vector3f l = r.normalized();
        Eigen::Vector3f v = (eye_pos - point).normalized();
        Eigen::Vector3f h = (l + v).normalized();
        Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
        Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity) / (r.dot(r)) * std::max((float)0.0, normal.normalized().dot(l));
        Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / (r.dot(r)) * std::max((float)0.0, pow(normal.normalized().dot(h), p));
        // components are. Then, accumulate that result on the *result_color* object.
        result_color = result_color + ambient + diffuse + specular;  
    }
 
    return result_color * 255.f;
} 

我们编译，在命令行输入命令

./Rasterizer output.png phong

texture_fragment_shader()的实现

纹理shader的实现其实就是用u,v去纹理图去找对应的颜色，我们需要知道该点像素的u和v，需要使用重心公式，其实现方式为：

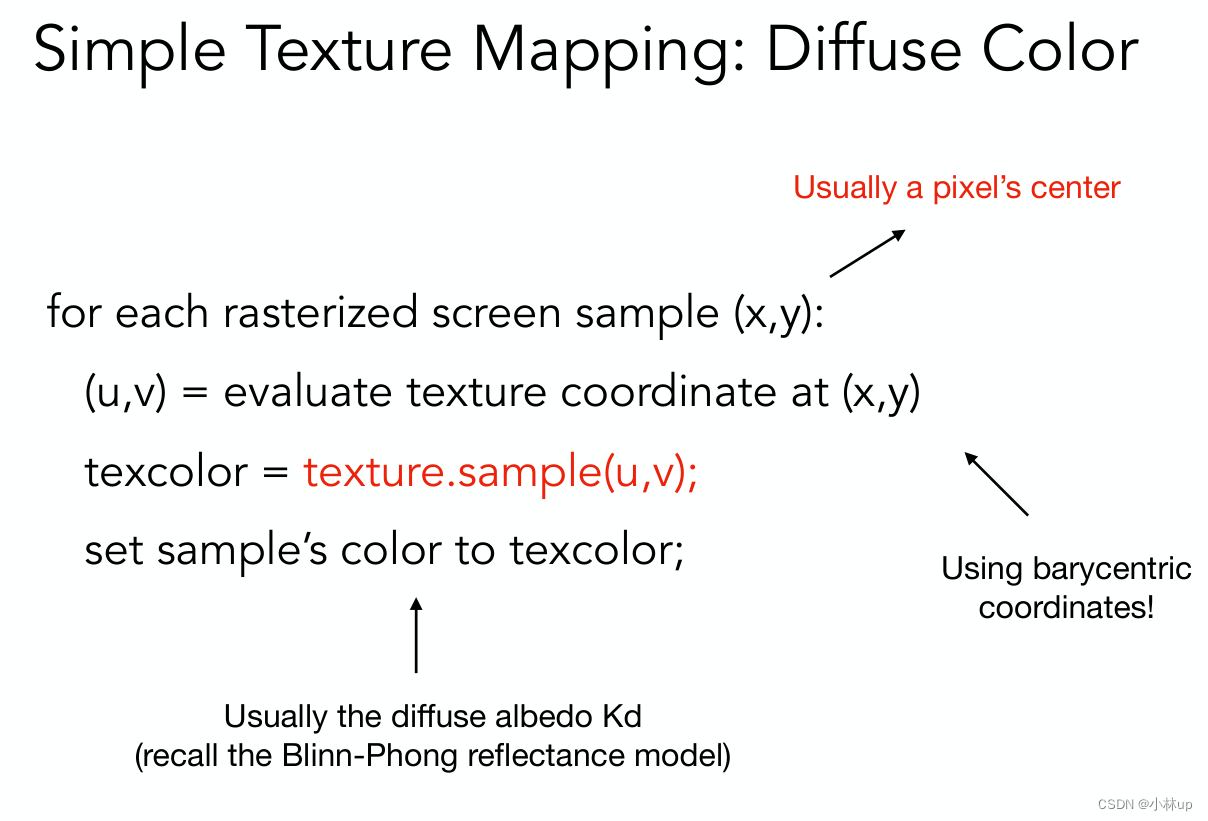
详细原理可以看：计算机图形学七：纹理映射(Texture Mapping)及Mipmap技术

Eigen::Vector3f texture_fragment_shader(const fragment_shader_payload& payload)
{
    Eigen::Vector3f return_color = {0, 0, 0};
    if (payload.texture)
    {
        // TODO: Get the texture value at the texture coordinates of the current fragment
        float u = payload.tex_coords[0];
        float v = payload.tex_coords[1];
        return_color = payload.texture->getColor(u, v);
    }
    Eigen::Vector3f texture_color;
    texture_color << return_color.x(), return_color.y(), return_color.z();

    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = texture_color / 255.f;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = texture_color;
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    Eigen::Vector3f result_color = {0, 0, 0};

    for (auto& light : lights)
    {
        // TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular* 
        // components are. Then, accumulate that result on the *result_color* object.
               // TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular* 
        Eigen::Vector3f r = light.position - point;
        Eigen::Vector3f l = r.normalized();
        Eigen::Vector3f v = (eye_pos - point).normalized();
        Eigen::Vector3f h = (l + v).normalized();
        Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
        Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity) / (r.dot(r)) * std::max((float)0.0, normal.dot(l));
        Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / (r.dot(r)) * std::max((float)0.0, pow(normal.dot(h), p));
        // components are. Then, accumulate that result on the *result_color* object.
        
        result_color = result_color + ambient + diffuse + specular; 
    }

    return result_color * 255.f;
}

和Phong Shading差不多，只不过这里我们使用的颜色要从纹理获得（实现的原理也很简单，通过u和v进行颜色的映射），而不是想Phong Shading里使用的是模型自己的颜色，关键代码在这里：

if (payload.texture)
{
    // TODO: Get the texture value at the texture coordinates of the current fragment
    float u = payload.tex_coords[0];
    float v = payload.tex_coords[1];
    return_color = payload.texture->getColor(u, v);
}

这里的tex_coords是通过rasterize_triangle()函数而来（回想我们在这个函数进行了纹理、法线、纹理坐标、颜色的插值得到像素点的最终渲染的属性，最后生成一个payload作为参数给渲染器帮我们着色，tex_coords在这个函数里是interpolated_texcoords，它是通过三角形的三个顶点的纹理坐标得来的，而三角形的三个纹理坐标我们是在main函数通过setTexCoord函数实现的）。

我们可以查看getColor源码的实现，注意这里为了防止数组的越界，我们需要给u和v设定范围限制（对应前面的四句if代码）。

Eigen::Vector3f getColor(float u, float v)
{

    if(u<0) u=0;
    if(v<0) v=0;
    if(u>1) u=1;
    if(v>1) v=1;

    auto u_img = u * width;
    auto v_img = (1 - v) * height;

    auto color = image_data.at<cv::Vec3b>(v_img, u_img);
    return Eigen::Vector3f(color[0], color[1], color[2]);
}

我们编译，在命令行输入命令

./Rasterizer output.png texture

bump_fragment_shader()的实现

bump mapping的思想是在像素的表面进行微小的高度变化（使用纹理）计算扰动点的法向量（只在渲染计算的时候做，实际并没有改变像素的高度）

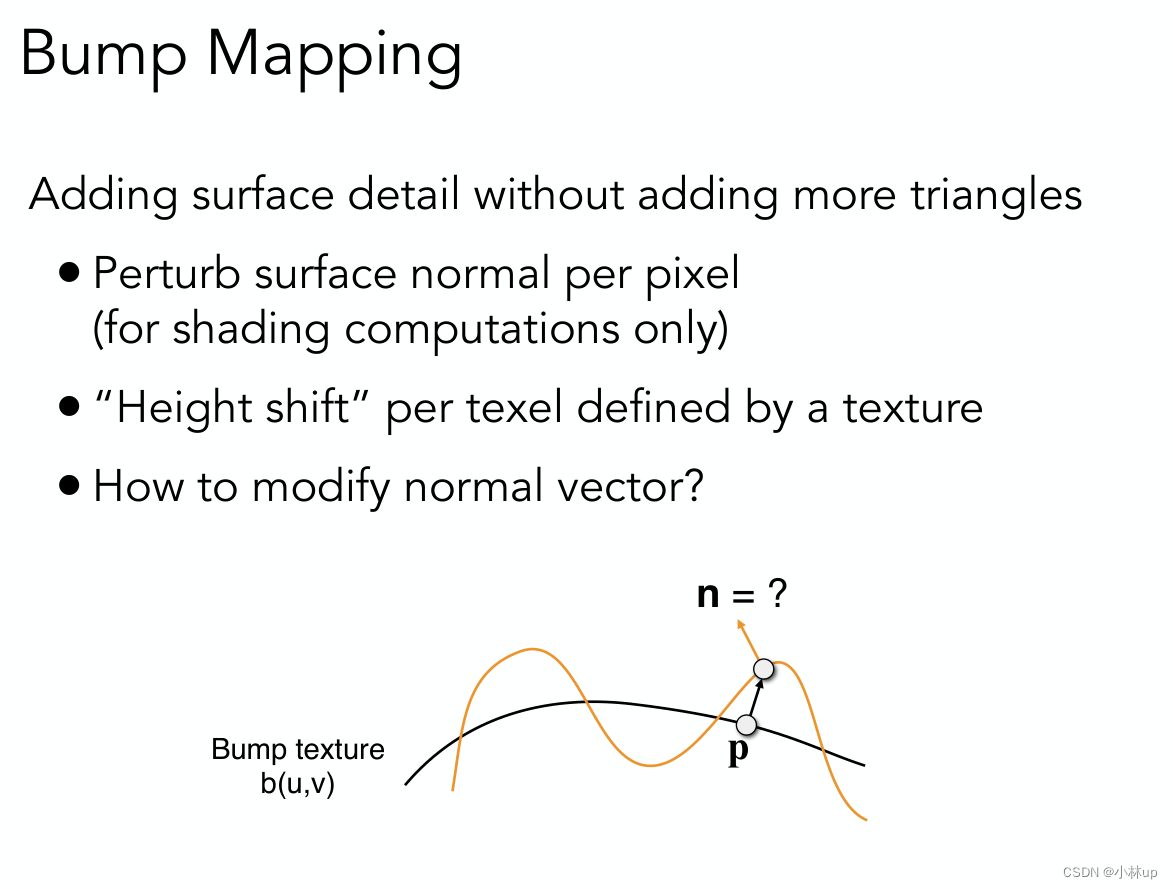
二维的实现

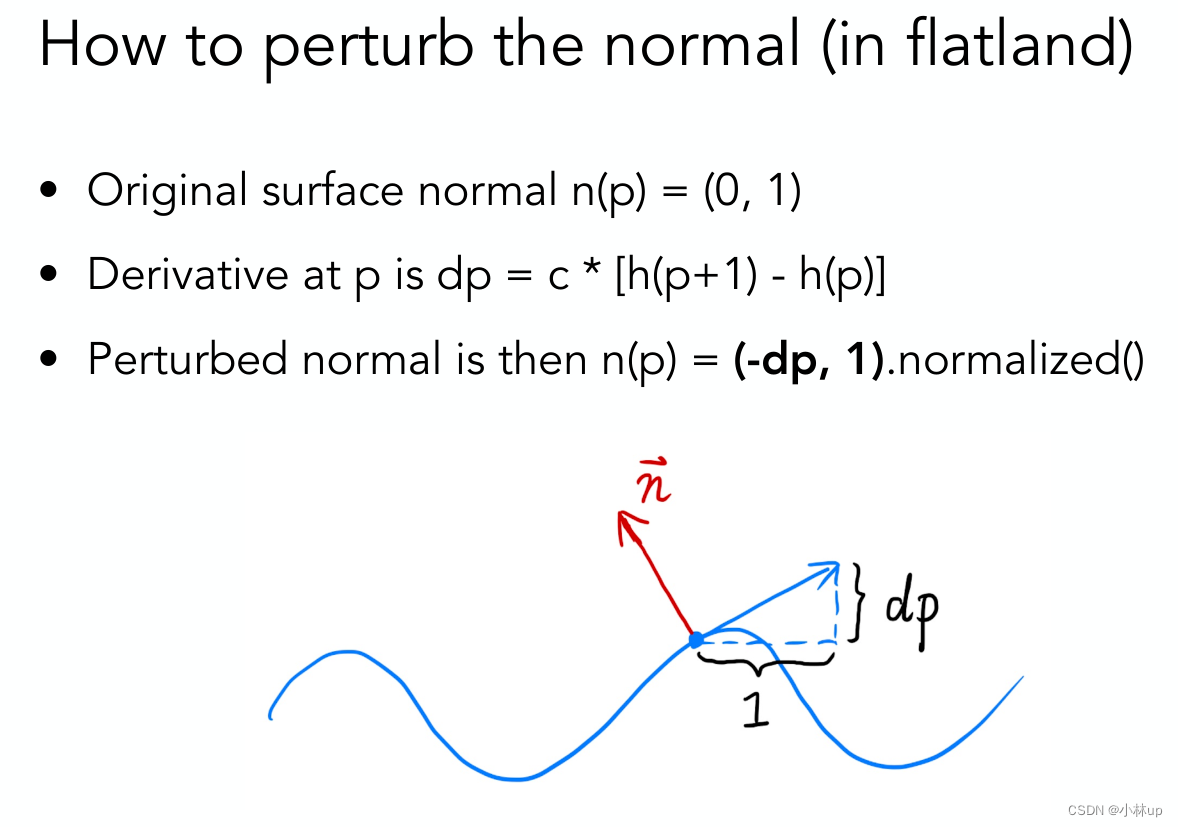
这里如图像素对应的切向量的是(1,dp)，所以法向量就是(-dp,1).。

三维的实现也是同样的，沿u方向和v方向的的切向量分别是(1,0,dp/du)和(0,1,dp/dv)（u和v是纹理坐标的方向，对应的是x轴和y轴，u和v方向垂直）。所以法向量要和这两个切向量垂直为(-dp/du,-dp/dv,1)，读者可以检验一下法向量和这两个切向量的垂直性。

根据注释写代码：这里使用的TBN矢量中，N是法线方向(normal)，代码里取的是$(x,y,z)$，B和T分别在切线空间里，注释提示我们T这里取的是$(\frac{xy}{\sqrt{(}{x}^2+z^2)},\sqrt{x^2+z^2},\frac{zy}{\sqrt{x^2+z^2}})$，尽管这个T的模是1，我们可以很容易地检验这是一个单位向量：

$$\begin{array}{rl}& {\left(\frac{xy}{\sqrt{x^2+z^2}}\right)}^2+{\left(\sqrt{x^2+z^2}\right)}^2+(\frac{zy}{\sqrt{x^2+z^2}}{)}^2\\ =& \frac{x^2{y}^2}{x^2+z^2}+x^2+z^2+\frac{z^2{y}^2}{x^2+z^2}\\ =& \frac{x^2{y}^2+x^4+2x^2{z}^2+z^4+z^2{y}^2}{x^2+z^2}\\ =& \frac{x^2{y}^2+x^4+x^2{z}^2+x^2{z}^2+z^4+z^2{y}^2}{x^2+z^2}\\ =& \frac{x^2(x^2+y^2+z^2)+z^2(x^2+y^2+z^2)}{x^2+z^2}(x^2+y^2+z^2=1)\\ =& \frac{x^2+z^2}{x^2+z^2}=1\end{array}$$

但是这里我认为是有问题的，但是它和N并不垂直。

$$\begin{array}{rl}& N\cdot T\\ =& (x,y,z)\cdot (\frac{xy}{\sqrt{(}{x}^2+z^2)},\sqrt{x^2+z^2},\frac{zy}{\sqrt{x^2+z^2}})\\ =& \frac{2x^{2}y+2z^{2}y}{\sqrt{x^2+z^2}}\end{array}$$

正确的应该是：$T=(-\frac{xy}{\sqrt{(}{x}^2+z^2)},\sqrt{x^2+z^2},-\frac{zy}{\sqrt{x^2+z^2}})$，这个博客画了这个T在三维坐标下的图（TBN三个矢量应该是相互垂直的！）,画得还是比较清楚的【图源games101——作业3】：

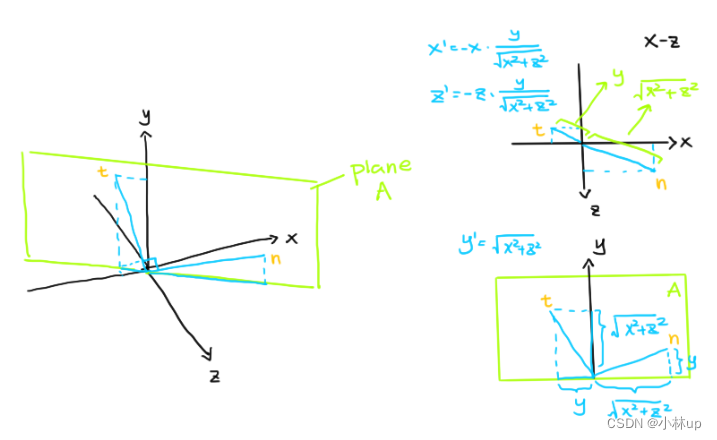
而B向量就是T和N的叉乘的结果了

Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload& payload)
{
    
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = payload.color;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = payload.color; 
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;


    float kh = 0.2, kn = 0.1;

    // TODO: Implement bump mapping here
    // Let n = normal = (x, y, z)
    // Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
    // Vector b = n cross product t
    // Matrix TBN = [t b n]
    // dU = kh * kn * (h(u+1/w,v)-h(u,v))
    // dV = kh * kn * (h(u,v+1/h)-h(u,v))
    // Vector ln = (-dU, -dV, 1)
    // Normal n = normalize(TBN * ln)
    float x = normal.x();
    float y = normal.y();
    float z = normal.z();
    Eigen::Vector3f t = {-x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),-z*y/sqrt(x*x+z*z)};
    Eigen::Vector3f b = normal.cross(t);
    Eigen::Matrix3f TBN;
    TBN << t.x(), b.x(), normal.x(),
                    t.y(), b.y(), normal.y(),
                    t.z(), b.z(), normal.z();
    float u = payload.tex_coords.x();
    float v = payload.tex_coords.y();
    float w = payload.texture->width;
    float h = payload.texture->height;
    float dU = kh * kn * (payload.texture->getColor(u + 1.0 / w, v).norm() - payload.texture->getColor(u, v).norm());
    float dV = kh * kn * (payload.texture->getColor(u, v + 1.0 / h).norm() - payload.texture->getColor(u, v). norm());
Eigen::Vector3f ln = {-dU, -dV, 1};
normal = (TBN * ln).normalized();
    


    Eigen::Vector3f result_color = {0, 0, 0};
    result_color = normal;

    return result_color * 255.f;
}

我们用下面的代码得到全局的TBN矩阵（我们最终的法向量还是要在相机空间里表示的，这是一个全局的变换矩阵）：

Eigen::Vector3f t = {-x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),-z*y/sqrt(x*x+z*z)};
Eigen::Vector3f b = normal.cross(t);
Eigen::Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
                t.y(), b.y(), normal.y(),
                t.z(), b.z(), normal.z();

然后我们需要计算再沿纹理图u和v方向的像素的变化量，计算导数用的是差分的方式再乘上一个系数：

float dU = kh * kn * (payload.texture->getColor(u + 1.0 / w, v).norm() - payload.texture->getColor(u, v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1.0 / h).norm() - payload.texture->getColor(u, v). norm());

注释提示这样求扰动后的法向量：

// Vector ln = (-dU, -dV, 1)
// Normal n = normalize(TBN * ln)

是先求扰动后的法向量（但没有归一化）再转换为相机空间的法向量，然后再归一化，而不是像ppt说的先对法向量归一化再转换到相机空间，猜测把归一化放到后面能减少一定的浮点误差，提前归一化要进行开平方根操作会造成变换到相机空间的误差。

Eigen::Vector3f ln = {-dU, -dV, 1};
normal = (TBN * ln).normalized();

我们编译，在命令行输入命令

./Rasterizer output.png bump

displacement_fragment_shader()的实现

位移贴图displacement mapping除了类似凹凸贴图，改变了法向量，而且实际移动了三维空间中点的位置，进而直接影响 Blinn-Phong 模型中的$l$和$v$。

Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload& payload)
{
    
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = payload.color;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = payload.color; 
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    float kh = 0.2, kn = 0.1;
    
    // TODO: Implement displacement mapping here
    // Let n = normal = (x, y, z)
    // Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
    // Vector b = n cross product t
    // Matrix TBN = [t b n]
    // dU = kh * kn * (h(u+1/w,v)-h(u,v))
    // dV = kh * kn * (h(u,v+1/h)-h(u,v))
    // Vector ln = (-dU, -dV, 1)
    // Position p = p + kn * n * h(u,v)
    // Normal n = normalize(TBN * ln)
     float x = normal.x();
    float y = normal.y();
    float z = normal.z();
    Eigen::Vector3f t = {x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z)};
    Eigen::Vector3f b = normal.cross(t);
    Eigen::Matrix3f TBN;
    TBN << t.x(), b.x(), normal.x(),
                    t.y(), b.y(), normal.y(),
                    t.z(), b.z(), normal.z();
    float u = payload.tex_coords.x();
    float v = payload.tex_coords.y();
    float w = payload.texture->width;
    float h = payload.texture->height;
    float dU = kh * kn * (payload.texture->getColor(u + 1.0/w, v).norm() - payload.texture->getColor(u, v).norm());
    float dV = kh * kn * (payload.texture->getColor(u, v + 1.0 / h).norm() - payload.texture->getColor(u, v). norm());
    Eigen::Vector3f ln = {-dU, -dV, 1};
    point = point + kn * normal * payload.texture->getColor(u, v).norm();
    normal = (TBN * ln).normalized();


    Eigen::Vector3f result_color = {0, 0, 0};

    for (auto& light : lights)
    {
        // TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular* 
        Eigen::Vector3f r = light.position - point;
        Eigen::Vector3f l = r.normalized();
        Eigen::Vector3f v = (eye_pos - point).normalized();
        Eigen::Vector3f h = (l + v).normalized();
        Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
        Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity) / (r.dot(r)) * std::max((float)0, normal.dot(l));
        Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / (r.dot(r)) * std::max((float)0, pow(normal.dot(h), p));
        // components are. Then, accumulate that result on the *result_color* object.
        result_color = result_color + ambient + diffuse + specular; 
    }

    return result_color * 255.f;
}

和bump mapping最主要的区别在于：

point = point + kn * normal * payload.texture->getColor(u, v).norm();

改变了顶点的坐标（沿着原来的发现的方向），顶点的坐标等于原顶点的坐标加法线向量乘系数kn乘纹理在该位置的颜色的模长，然后也是使用phong shading来渲染

我们编译，输入命令：

./Rasterizer output.png displacement

尝试其他的obj模型

参考的Games101｜作业3 + shading + 双线性插值 + 疑惑

需要安装meshlab，参考ubuntu安装meshlab，全网最简单的方法

记得改路径

记得该eye_pos！！！没有改可能会出现段错误，图形跑到700*700的框框外面去了，找不到对应的颜色。

输出时应该是下面这样（输出为obj）

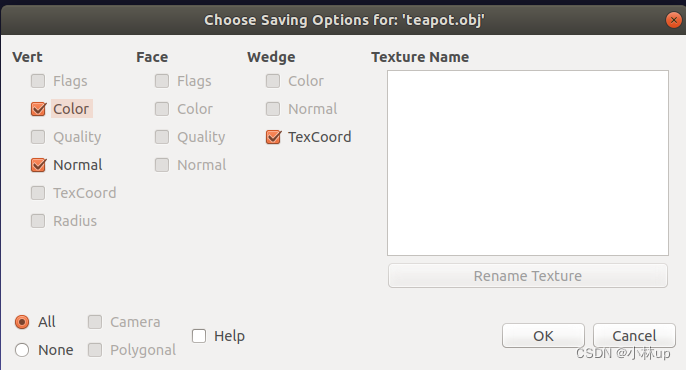
然后文件夹下除了obj还有obj.mtl格式的文件，没有的话texture可能出问题（我这里保存的是teapot2.obj和teapot.obj.mtl）

记得main函数修改路径：obj_path、loadout、texture_path。

normal shader

phong shader

bump shader 有点过于粗糙的感觉

texture shader

displacement shader

双线性插值

找个压缩图片的网站，我们把小奶牛的texture压缩为512*512的（原来是1024*1024的）保存下来，在把texture的路径改为这个512*512的。
OKTools-图片压缩

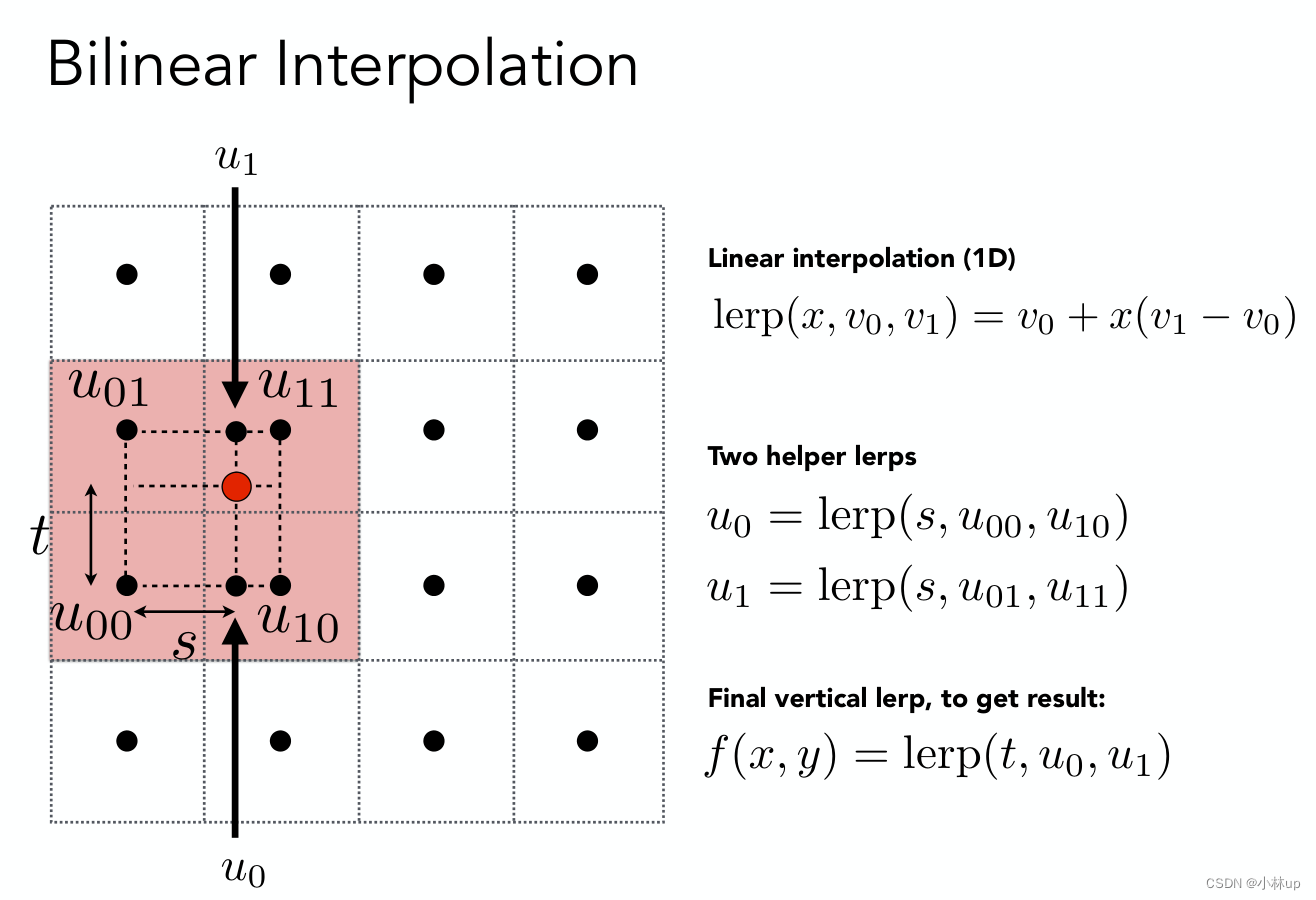
找到四个顶点，先沿宽度方向插值，再沿高度方向插值。

getColorBilinear

Eigen::Vector3f getColorBilinear(float u, float v)
    {

        if(u<0) u=0;
        if(v<0) v=0;
        if(u>1) u=1;
        if(v>1) v=1;

        auto u_img = u * width;
        auto v_img = (1 - v) * height;
        float ul = floor(u_img);
        float uh = ceil(u_img);
        float vl = floor(v_img);
        float vh = ceil(v_img);
        float s = (u_img - ul) / (uh - ul);
        float t = (v_img - vl) / (vh - vl);

        // 双线性插值
        auto color_o = image_data.at<cv::Vec3b>(v_img, u_img);
        auto color_00 = image_data.at<cv::Vec3b>(vl, ul);//color的序号按照u,v的顺序来，大值对应h，小值对应l
        auto color_01 = image_data.at<cv::Vec3b>(vh, ul);
        auto color_10 = image_data.at<cv::Vec3b>(vl, uh);
        auto color_11 = image_data.at<cv::Vec3b>(vh, uh);
        auto color_lerp1 = (1 - s) * color_00 + s * color_10;
        auto color_lerp2 = (1 - s) * color_01 + s * color_11;

        auto color = (1 - t) * color_lerp1 + t * color_lerp2 ;
        return Eigen::Vector3f(color[0], color[1], color[2]);
    }

};

记得把texture_fragment_shader获取颜色的方法改为双线性插值的方法getColorBilinear，主要是这一段代码：

if (payload.texture)
{
    // TODO: Get the texture value at the texture coordinates of the current fragment
    float u = payload.tex_coords[0];
    float v = payload.tex_coords[1];
    // return_color = payload.texture->getColor(u, v);
    return_color = payload.texture->getColorBilinear(u, v);

}

测试：使用双线性插值：

不使用双线性插值：

可以看到效果还是很明显的。

另外关于作业3框架的一些问题可以参考这篇知乎的文章，写的很好：《GAMES101》作业框架问题详解，尽管作业里的深度插值用的不是真实的深度，但是我们还是得到了正确的效果（题目也说了，深度处理为了正值，离相机越近深度是越小的，深度相当于做了一个线性的映射到0.1到50，不过深度的大小情况是不变的，该靠近相机的还是靠近相机，所以我们最后还是可以看到这只牛牛）。

其他记录：

+讨论区 › 作业3更正公告

• 讨论区 › [Lecture 9]为什么离视角近的像素点，对应的纹理区域越小？

• 讨论区 › 关于几个思路问题(学习习惯与学习方法)

• displacement 原理问题