灰度直方图均衡化讨论【个人原创】
目录
一、定义
我们在灰度直方图(grayscale histogram)的讨论中，对于输入图像中任意一像素(pixel)的灰度级 
，在输出图像中总能找到像素的灰度级
使得
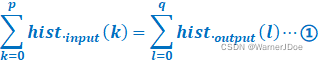
由①式我们显而易见可以得出：
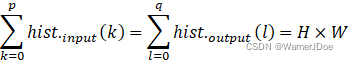
显然仅仅根据①式，想要实现直方图的均衡化是达不到的。如果使图像在所有灰度级上直方图均衡化，则需要在数学上求平均值，即理想状态下输出图像每个灰度级的个数：
([1]由于直方图横纵坐标取值均为非负整数，因此本文讨论一些数学关系需要根据实际做≈处理)
([2]每个直方图底边长为1，其右下角与所对应灰度级坐标刻度对齐，因此所有灰度级直方图底边长之和最大为255+1)
然而做到平均可能会造成原有亮度关系发生改变，为了保持这一关系不被均衡化打乱，那么在输出图像中对于任意灰度级q，需要有
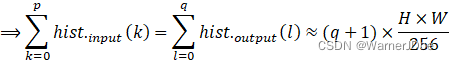
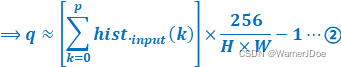
②式即为经过均衡化后输出图像中灰度级q的计算式。
二、几条性质
2.1 有界性
对于
，代入②式得
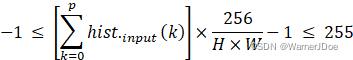
2.2 单调性
已知对于
，则有
对于
，易得
那么可知即随着k增加，和也随之增加。
2.3数量稳恒性
2.3.1 均衡化前后对应灰度级数量不变
假设原图数量级x经过均衡化后，对应生成灰度级y、z(y<z)，那么根据单调性
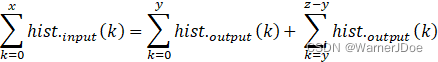
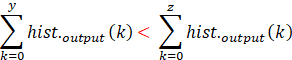
即z较y而言，更加亮。然而根据均衡化定义，可知
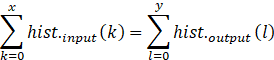
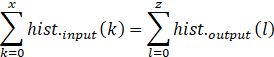
显然与上述不等式结论相矛盾，因此假设不成立。(其他假设情况可同理证明)
故均衡化前后对应灰度级数量保持不变。
2.3.2 均衡化前后对应灰度级像素数量不变
假设原图数量级x，其像素数量
经过均衡化后，分配至灰度级y、z(y<z)上，分别为
和
。
对于a<y，
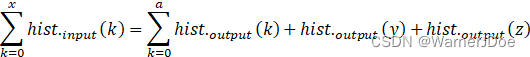
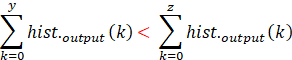
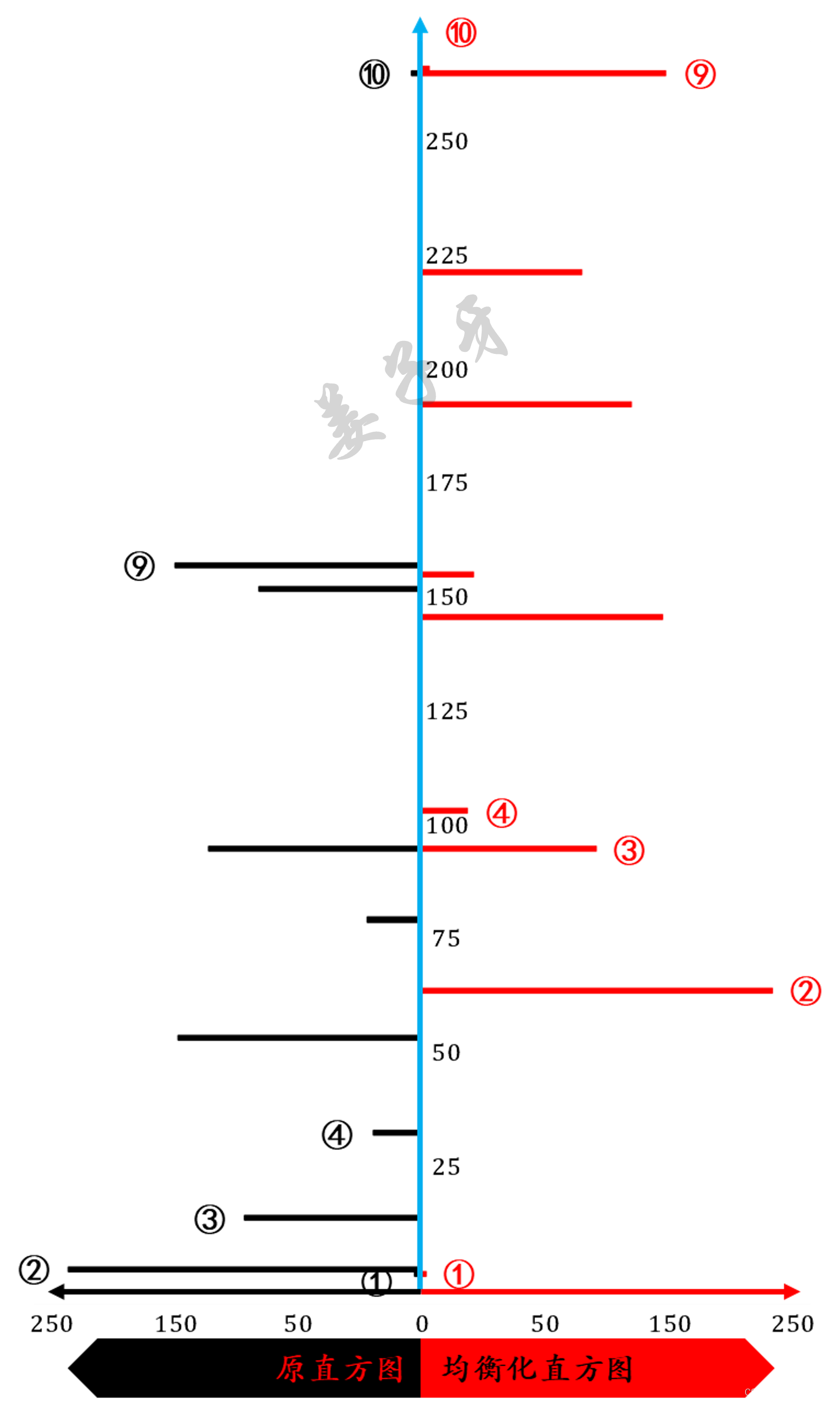
即z较y而言，更加亮。然而根据均衡化定义，可知
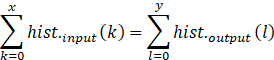
显然与上述不等式结论相矛盾，因此假设不成立。(其他假设情况可同理证明)
故均衡化前后对应灰度级像素数量保持不变。
三、对计算结果q处理的讨论
根据有界性的讨论可知，对于
，通过②式计算可得
。但实际上
，因此我们需要对②式计算结果做出调整以达到均衡化结果的可输出。
根据单调性可知，对于
，易得
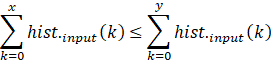
进而可得
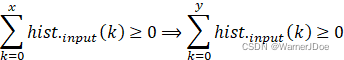
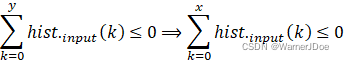
据此可得：计算式②中
的结果应当在k取值区间的左侧出现，且只会“连续出现”。
又根据数量稳恒性可知，如果出现
，那么q的灰度级数可能取值变成了257种，然而输入p只有256种可能。因此如果
，意味着q在[0,255]上一定出现某个灰度级出现“空隙”。
调整的操作，可以基于“空隙”采取不同策略。
暂时可以想到的简单策略有：
3.1 q=-1→q=0
指将均衡化计算得
的部分直接加到
上。
该方法代码实现较为简单，但是却在原理上部分违背了“均衡化后保持亮度关系不变”的原则。
3.2 q=-1 ~首个“空隙”整体+1
指计算结果中从
到第一个“空隙”之间的直方图整体灰度级+1以达到整体移动。
该方法需要首先判断
到第一个“空隙”的所有灰度级序号，然后将该区间所有灰度级+1处理。
该方法仍然改变了移动部分和不移动部分的亮度关系，但代码实现并不繁琐。
3.3 最大连续“空隙”缩减
指计算结果中群找到最大的连续“空隙”区间，将在此之前的灰度级整体+1。
该方法需要判断计算结果中所有的“空隙”区间(当然包括区间边界的灰度级序号)，相比较求得最大的区间，然后将区间边界灰度级序号之前的灰度级整体+1移动。
个人认为这是对计算所得的亮度关系改变最为温和的方法，但代码实现可能最为繁琐。
四、说明
以上均为个人不成熟的推论，欢迎与各位沟通交流，对我进行批评指正~谢谢！