直接插入排序和希尔排序

前言
排序: 所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序: 数据元素全部放在内存中的排序。
外部排序: 数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
概述
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
现实生活中,打扑克牌就是一个插入排序的例子

直接插入排序
本质
- 设一个待排序的数组,
a[1]是一个有序的序列 - 将后面的元素和已经排序好的元素进行比较。
图解:

分析
本篇文章,以从小到大的顺序排序为例
以其中一趟排序为例:
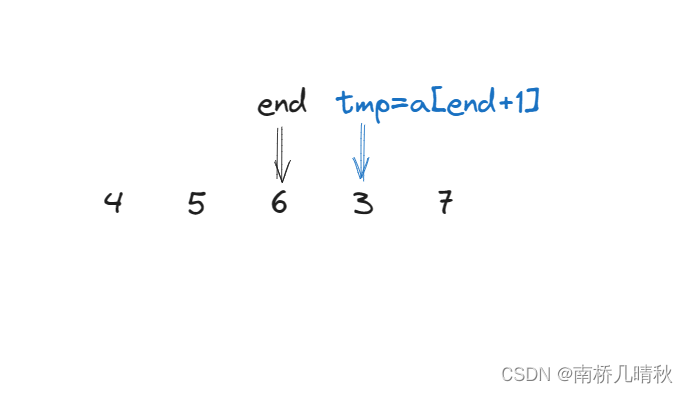
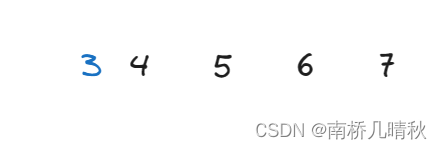
前面的4 5 6已经是排序好的数字,现在需要将元素3继续排序。
此时的end指向6,tmp指向的的是end+1的位置,即3。
将end和tmp进行比较,显然3<6,即tmp<end
此时将tmp拿出来,将end移动到tmp位置
end继续往前移动,继续和tmp比较
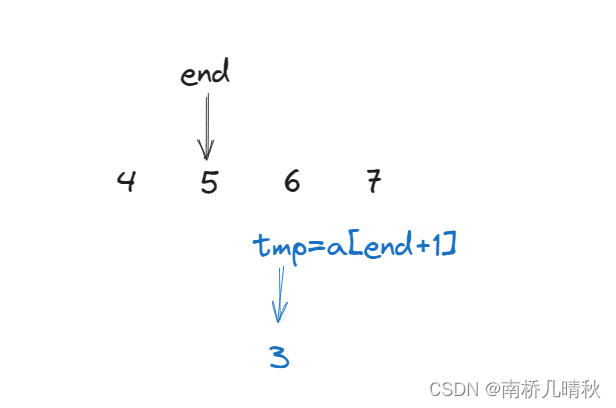
此时依然tmp<end,end还是需要往前移动,即end--
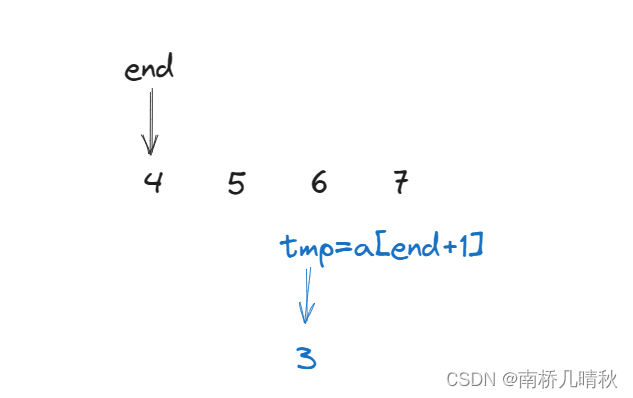
此时依然tmp<end,end还是需要往前移动,即end--
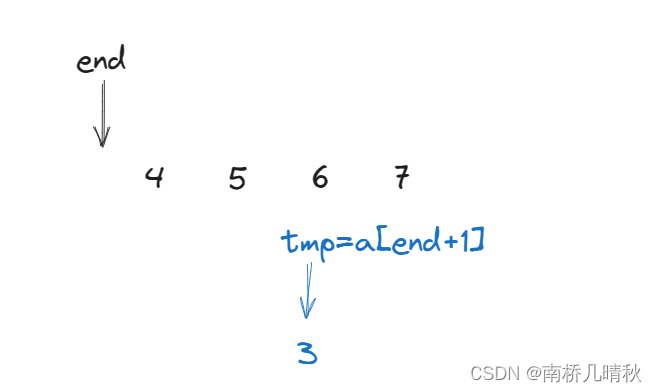
此时end<0,循环结束,无需再比较,直接将tmp元素插入到最前面。
一趟排序的代码:
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
因此一趟排序的终止条件为end<0
要想完成所有元素排序,在一趟排序的基础上套一个for循环。从第一个元素开始遍历,end=i,循环结束的标志是i<n-1,此时end指向的的是倒数第二个元素,tmp指向最后一个元素。
代码
# define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<assert.h>
void InsertSort(int*a,int n)
{
// [0,end] end+1
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
//输出排序后的数组
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
int main()
{
//测试
int a[] = { 3, 2, 6, 8, 4, 6, 0, 9, 5, 7, 1 };
InsertSort(a, sizeof(a) / sizeof(a[0]));
PrintArray(a, sizeof(a) / sizeof(a[0]));
return 0;
}
总结
直接插入排序适用于较为有序的元素
当元素较为有序时,时间复杂度为O(N)
当元素为逆序时,时间复杂度为O(N2)
希尔排序
希尔排序简单来说,可以分为两步,先进行分组排序,再进行插入排序。
先将整个待排序序列分割成几组,从而减少参与直接插入排序的数据量,对每组放分别进行直接插入排序,然后增加每组的数据量,重新分组。这样当经过几次分组排序后,整个序列中的记录“基本有序”时,再对整个序列进行一次直接插入排序。
一组一组排序
将待排序列9 8 7 6 6 5 4 3 2 1 0进行排序,先进行分组,小编以间隔3为一组,可得到以下分组方式:
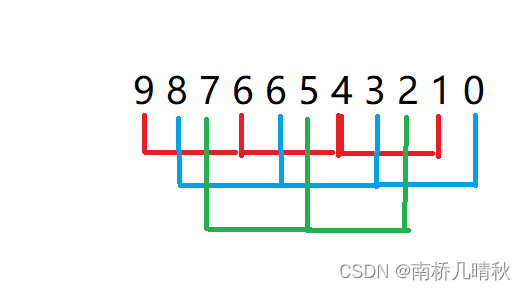
红色的为一组排序,蓝色的为一组排序,绿色为一组排序
先对红色的一组排序,红色的序列为9 6 4 1,进行直接插入排序,即1 4 6 9
然后对蓝色的一组排序,蓝色的序列为8 6 3 0,进行直接插入排序,即0 3 6 8
最后对绿色的一组排序,绿色的序列为7 5 2,进行直接插入排序,即2 5 7
此时的整个序列的顺序为1 0 2 4 3 5 6 6 7 9 8,待排序序列是一个较为有序的序列,这时直接使用插入排序,降低了插入排序的复杂度
int i = 0, j = 0;
int gap = 3;
for (i = 0; i < gap; i++)
{
for (j = i; j < n - gap; j = j + gap)
{
int end = j;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end = end - gap;
}
else
break;
}
a[end + gap] = tmp;
}
}
j == 0时,红色组进行排序
j == 1时,蓝色组进行排序
j == 2时,绿色组进行排序
多组同时进行
多组同时进行,只需要一个for循环,不需要再嵌套循环。
只需要将j一开始指向第一个待排序元素(是红色组的第一个元素),然后j++,指向第二个元素(蓝色组第一个元素),再j++,此时指向第三个元素(绿色组第一个元素)。
for (j = 0; j < n - gap; j ++)
{
int end = j;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end = end - gap;
}
else
break;
}
a[end + gap] = tmp;
}
无论是一组一组进行还是多组同时进行,都只是一个预排序,并没有完成整个跑排序
完整的代码
gap越大,大的值可以更快的跳到后面,小的值可以更快的跳到前面,越不接近有序
gap越小,跳的越慢,但是越接近有序,如果gap==1就是直接插入排序
那么,gap的值到底应该是多少??这个问题官方也没有一个直接的解答,但是有一个操作,可以解决这个问题:
gap > 1时是预排序,目的让他接近有序
gap == 1是直接插入排序,目的是让他有序
首先将gap的置为待排序元素的大小n,让gap循环一次就除以2,无论gap的值是多少,最终都会等于1;或者gap/3+1,无论gap的值是多少,最终都会等于1。gap==1时,是直接插入排序,不会再进入循环。
图解:
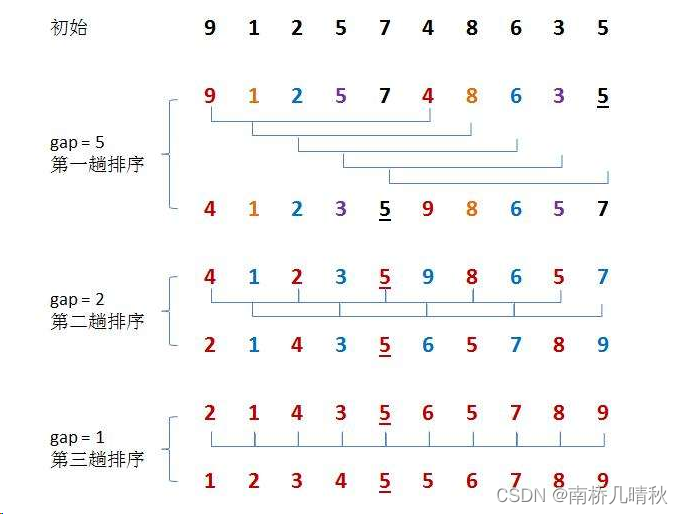
ShellSort排序代码:
void ShellSort(int* a, int n)
{
int gap = n;
// gap > 1时是预排序,目的让他接近有序
// gap == 1是直接插入排序,目的是让他有序
while (gap > 1)
{
//gap = gap / 2;
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
测试代码:
# define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
void ShellSort(int* a, int n)
{
int gap = n;
// gap > 1时是预排序,目的让他接近有序
// gap == 1是直接插入排序,目的是让他有序
while (gap > 1)
{
//gap = gap / 2;
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
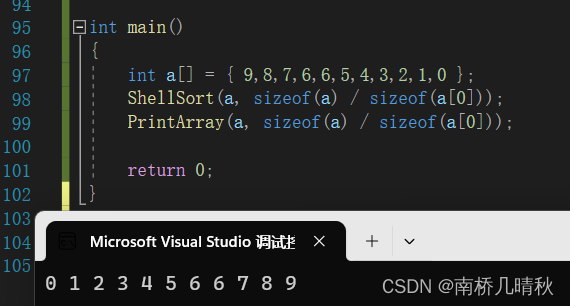
int main()
{
int a[] = { 9,8,7,6,6,5,4,3,2,1,0 };
ShellSort(a, sizeof(a) / sizeof(a[0]));
PrintArray(a, sizeof(a) / sizeof(a[0]));
return 0;
}
总结
希尔排序是在直接插入排序基础上完成的,希尔排序的时间复杂度的计算涉及数论,小编无法解读。直接排序的时间复杂度虽然是O(N2),但是不要小瞧它,比冒泡排序还是优秀很多。在冒泡排序直接插入排序,希尔排序中,希尔排序还是很优秀的。
