计算机图形学——二维变换
二维变换
概念
应用于对象几何描述并改变其位置、方向或者大小的变换叫做几何变换,有时候也被叫做建模变换。而本文仅讨论平面中的几何变换,即二维变换。
矩阵表示和齐次坐标
对于普通的2x2矩阵,我们总是要将平移项与其它变换对应的矩阵写成不同规格,为了统一形式且方便运算,我们需要将2x2的矩阵扩展到3x3。此时,二为坐标必须用三元向量来表示。标准实现技术是将二维坐标 ( x , y ) (x,y) (x,y)扩充到三维 ( x h , y h , h ) (x_h,y_h,h) (xh,yh,h),这称为齐次坐标,这个过程就被叫做齐次化。
对于每一个维度有
x
=
x
h
h
,
y
=
y
h
h
x = \frac{x_h}{h},y=\frac{y_h}{h}
x=hxh,y=hyh
其中非零值
h
h
h被称为齐次参数。
显然对于齐次参数,可以有无数个非零值,同样也意味着有无数个等价的齐次表达式。既然如此,为了方便计算,不妨令 h = 1 h=1 h=1。
平移变换
对于平移变换,我们可有参数方程
{
x
′
=
x
+
δ
x
y
′
=
y
+
δ
y
\begin{cases} x^{'}=x+\delta x \\ y^{'} = y+\delta y \end{cases}
{x′=x+δxy′=y+δy
我们将方程组转换为矩阵的形式
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
1
0
0
0
1
0
δ
x
δ
y
1
]
\begin{bmatrix} x'& y'& 1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0\\ 0& 1& 0\\ \delta x& \delta y & 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
10δx01δy001
旋转变换
对于一个复杂的图形的旋转,我们可以看做是多个点在同时旋转。因此只需要研究出一个点的旋转变换方法就可以了。
我们不妨令点为平面任意一点,其绕原点进行旋转变换,该点的运动轨迹一定是一个以该点到原点连线为半径的圆弧。那么问题就简单了,对于旋转任意角度,我们只需要用圆的参数方程就能搞定,
{
x
=
cos
θ
y
=
sin
θ
\begin{cases} x = \cos{\theta} \\ y = \sin{\theta} \end{cases}
{x=cosθy=sinθ
对于我们假设旋转了
α
\alpha
α的弧度(逆时针为正方向),则有
{
x
′
=
cos
(
θ
+
α
)
=
cos
θ
cos
α
−
sin
θ
sin
α
=
x
cos
α
−
y
sin
α
y
′
=
sin
(
θ
+
α
)
=
sin
θ
cos
α
+
cos
θ
sin
α
=
x
sin
α
+
y
cos
α
\begin{cases} x' = \cos{(\theta+\alpha)}=\cos{\theta}\cos{\alpha}-\sin{\theta}\sin{\alpha}=x\cos{\alpha}-y\sin{\alpha} \\ y' = \sin{(\theta+\alpha)}=\sin{\theta}\cos{\alpha}+\cos{\theta}\sin{\alpha}=x\sin{\alpha}+y\cos{\alpha} \end{cases}
{x′=cos(θ+α)=cosθcosα−sinθsinα=xcosα−ysinαy′=sin(θ+α)=sinθcosα+cosθsinα=xsinα+ycosα
很显然对应矩阵形式为
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
cos
α
sin
α
0
−
sin
α
cos
α
0
0
0
1
]
\begin{bmatrix} x'&y'&1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} \cos{\alpha}& \sin{\alpha}& 0 \\ -\sin{\alpha}& \cos{\alpha}& 0 \\ 0& 0& 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
cosα−sinα0sinαcosα0001
那么问题来了,如果所绕的旋转点不是原点怎么办呢?
前面已经讲过平移变换了,只需要平移坐标系原点至该点(移轴),再进行旋转,最后平移回去就行了。
不妨令被围绕点坐标为
P
(
x
1
,
y
1
)
P(x_1,y_1)
P(x1,y1),则该流程的矩阵运算如下:
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
1
0
0
0
1
0
−
x
1
−
y
1
1
]
⋅
[
cos
α
sin
α
0
−
sin
α
cos
α
0
0
0
1
]
⋅
[
1
0
0
0
1
0
x
1
y
1
1
]
\begin{bmatrix} x'& y'& 1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0\\ 0& 1& 0\\ -x_1& -y_1 & 1 \end{bmatrix} \cdot \begin{bmatrix} \cos{\alpha}& \sin{\alpha}& 0 \\ -\sin{\alpha}& \cos{\alpha}& 0 \\ 0& 0& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0\\ 0& 1& 0\\ x_1& y_1 & 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
10−x101−y1001
⋅
cosα−sinα0sinαcosα0001
⋅
10x101y1001
如果你对平移坐标系难以理解,不妨将坐标轴与平面想象成两个分离的东西。以坐标轴往右移动为例,则对于平面上的点来讲,就相当于坐标轴不动点向左平移。(平移坐标系只是移动的轴,不带平面上其他点,否则你会得到相反的结果!)
缩放变换
首先给出参数方程
{
x
′
=
s
x
x
y
′
=
s
y
y
\begin{cases} x' = s_xx \\ y' = s_yy \end{cases}
{x′=sxxy′=syy
对应矩阵运算为
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
s
x
0
0
0
s
y
0
0
0
1
]
\begin{bmatrix} x'&y'&1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} s_x& 0& 0 \\ 0& s_y& 0 \\ 0& 0& 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
sx000sy0001
对称变换
关于对称变换可以是轴对称或者点对称。
我们先来看关于y轴对称:只需要纵坐标不变,横坐标取相反数即可。
矩阵运算如下
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
−
1
0
0
0
1
0
0
0
1
]
\begin{bmatrix} x'&y'&1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} -1& 0& 0 \\ 0& 1& 0 \\ 0& 0& 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
−100010001
同理可得关于y轴对称矩阵运算
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
1
0
0
0
−
1
0
0
0
1
]
\begin{bmatrix} x'&y'&1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0 \\ 0& -1& 0 \\ 0& 0& 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
1000−10001
那么对于原点对称就有
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
−
1
0
0
0
−
1
0
0
0
1
]
\begin{bmatrix} x'&y'&1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} -1& 0& 0 \\ 0& -1& 0 \\ 0& 0& 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
−1000−10001
如果是对于平面中任意一点
P
(
x
1
,
y
1
)
P(x_1,y_1)
P(x1,y1)对称,则平移坐标系原点至该点,然后进行关于原点的对称,再平移回去就行。
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
1
0
0
0
1
0
−
x
1
−
y
1
1
]
⋅
[
−
1
0
0
0
−
1
0
0
0
1
]
⋅
[
1
0
0
0
1
0
x
1
y
1
1
]
\begin{bmatrix} x'& y'& 1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0\\ 0& 1& 0\\ -x_1& -y_1 & 1 \end{bmatrix} \cdot \begin{bmatrix} -1& 0& 0 \\ 0& -1& 0 \\ 0& 0& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0\\ 0& 1& 0\\ x_1& y_1 & 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
10−x101−y1001
⋅
−1000−10001
⋅
10x101y1001
如果是关于平面内任意一条直线对称,那比较麻烦了,你需要先平移坐标系到直线的一点,并旋转坐标系使x轴与直线重合,然后进行关于x轴的对称变换,再旋转回去,然后再平移回去。
特别地,如果直线斜率不存在,平移后直线与y轴重合,那么直接进行关于y轴对称然后再平移回去即可。
注意该过程的顺序,因为矩阵并不满足交换律!
这里实际上是有两个大坑的,我们不妨假设直线经过的两点分别为
A
(
x
1
,
y
1
)
,
B
(
x
2
,
y
2
)
A(x_1,y_1),B(x_2,y_2)
A(x1,y1),B(x2,y2)
不失一般性,我们令
x
1
<
=
x
2
x_1<=x_2
x1<=x2
我们在上面已经说过直线斜率不存在的情况了,这里仅讨论直线斜率存在的情况。直线斜率为
k
=
δ
x
δ
y
=
y
2
−
y
1
x
2
−
x
1
k = \frac{\delta x}{\delta y}=\frac{y_2-y_1}{x_2-x_1}
k=δyδx=x2−x1y2−y1
我们想要得到直线与x轴的夹角,可以利用反正切函数
θ
=
arctan
k
\theta = \arctan{k}
θ=arctank
但是事实就是如此吗?注意反正切函数的取值范围为
(
−
π
2
,
π
2
)
(-\frac{\pi}{2},\frac{\pi}{2})
(−2π,2π),而直线倾斜角范围是
[
0
,
π
]
[0,\pi]
[0,π],即使挖去了
π
2
\frac{\pi}{2}
2π这个点(因为我们不讨论这种情况),范围仍不一致!
我们记倾斜角为
α
\alpha
α,则有
α
=
{
θ
,
0
≤
θ
<
π
2
π
+
θ
,
θ
<
0
\alpha= \begin{cases} \theta,& 0\le \theta<\frac{\pi}{2} \\ \pi+\theta, &\theta<0 \end{cases}
α={θ,π+θ,0≤θ<2πθ<0
现在开始进入第二个坑了,我们进行旋转倾斜角的时候,是顺时针还是逆时针?
我们不妨站在坐标系的角度来看,逆时针旋转倾斜角的角度,就相当于顺时针旋转图形这个角度。
也就是说,我们在进行第一次旋转变换时输入的角度参数应该为 − α -\alpha −α
综上所述,矩阵运算为
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
1
0
0
0
1
0
−
x
1
−
y
1
1
]
⋅
[
cos
α
−
sin
α
0
sin
α
cos
α
0
0
0
1
]
⋅
[
1
0
0
0
−
1
0
0
0
1
]
⋅
[
cos
α
sin
α
0
−
sin
α
cos
α
0
0
0
1
]
⋅
[
1
0
0
0
1
0
x
1
y
1
1
]
\begin{bmatrix} x'& y'& 1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0\\ 0& 1& 0\\ -x_1& -y_1 & 1 \end{bmatrix} \cdot \begin{bmatrix} \cos{\alpha}& -\sin{\alpha}& 0 \\ \sin{\alpha}& \cos{\alpha}& 0 \\ 0& 0& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0 \\ 0& -1& 0 \\ 0& 0& 1 \end{bmatrix} \cdot \begin{bmatrix} \cos{\alpha}& \sin{\alpha}& 0 \\ -\sin{\alpha}& \cos{\alpha}& 0 \\ 0& 0& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0\\ 0& 1& 0\\ x_1& y_1 & 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
10−x101−y1001
⋅
cosαsinα0−sinαcosα0001
⋅
1000−10001
⋅
cosα−sinα0sinαcosα0001
⋅
10x101y1001
错切变换
错切变换实际上是物体在投影平面上非垂直投影的结果。一般为水平错切和垂直错切,也可以同时对两个方向进行错切。
我们先来看看沿y轴方向的错切
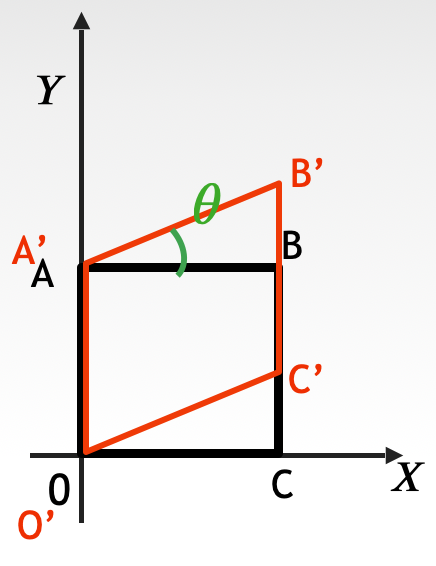
显然有方程
{
x
′
=
x
y
′
=
y
+
x
tan
θ
\begin{cases} x' = x \\ y' = y+x\tan{\theta} \end{cases}
{x′=xy′=y+xtanθ
有矩阵运算
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
1
tan
θ
0
0
1
0
0
0
1
]
\begin{bmatrix} x'&y'&1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& \tan{\theta}& 0 \\ 0& 1& 0 \\ 0& 0& 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
100tanθ10001
同理可得沿着x方向的错切矩阵运算
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
1
0
0
tan
θ
1
0
0
0
1
]
\begin{bmatrix} x'&y'&1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& 0& 0 \\ \tan{\theta}& 1& 0 \\ 0& 0& 1 \end{bmatrix}
[x′y′1]=[xy1]⋅
1tanθ0010001
同时沿着x方向和y方向的错切
[
x
′
y
′
1
]
=
[
x
y
1
]
⋅
[
1
tan
α
0
tan
θ
1
0
0
0
1
]
α
,
θ
∈
(
−
π
2
,
π
2
)
\begin{bmatrix} x'&y'&1 \end{bmatrix} = \begin{bmatrix} x& y& 1 \end{bmatrix} \cdot \begin{bmatrix} 1& \tan{\alpha}& 0 \\ \tan{\theta}& 1& 0 \\ 0& 0& 1 \end{bmatrix} \space \alpha,\theta \in (-\frac{\pi}{2},\frac{\pi}{2})
[x′y′1]=[xy1]⋅
1tanθ0tanα10001
α,θ∈(−2π,2π)
刚体变换
如果一个矩阵仅包含平移参数和旋转参数,那么它就是一个刚体变换矩阵
$$
\begin{bmatrix}
x’& y’& 1
\end{bmatrix}
\begin{bmatrix}
x& y& 1
\end{bmatrix}
\cdot
\begin{bmatrix}
r_{xx}& r_{yx}& 0\
r_{xy}& r_{yy}& 0\
tr_{x}& tr_{y}& 1
\end{bmatrix}
$$
对于刚体变换左上角的2x2矩阵满足正交矩阵的特性。也就是说对于两个列向量 [ r x x r x y ] T \begin{bmatrix}r_{xx}& r_{xy} \end{bmatrix}^{T} [rxxrxy]T和 [ r y x r y y ] T \begin{bmatrix}r_{yx}& r_{yy} \end{bmatrix}^{T} [ryxryy]T(或者两个行向量)形成单位向量的正交组,这样的向量也称为正交向量组。
对于每个向量具有单位长度,并且数量积为0:
r
x
x
2
+
r
x
y
2
=
r
y
x
2
+
r
y
y
2
=
1
r
x
x
r
y
x
+
r
x
y
r
y
y
=
0
r_{xx}^2+r_{xy}^2=r_{yx}^2+r_{yy}^2=1 \\ r_{xx}r_{yx}+r_{xy}r_{yy} = 0
rxx2+rxy2=ryx2+ryy2=1rxxryx+rxyryy=0
如果这些向量通过旋转矩阵进行变换,则可得出x方向和y方向的单位向量
[
r
x
x
r
x
y
1
]
⋅
[
r
x
x
r
y
x
0
r
x
y
r
y
y
0
0
0
1
]
=
[
1
0
1
]
\begin{bmatrix} r_{xx}& r_{xy}& 1 \end{bmatrix} \cdot \begin{bmatrix} r_{xx}& r_{yx}& 0\\ r_{xy}& r_{yy}& 0\\ 0& 0& 1 \end{bmatrix} =\begin{bmatrix} 1& 0& 1 \end{bmatrix}
[rxxrxy1]⋅
rxxrxy0ryxryy0001
=[101]
[ r y x r y y 1 ] ⋅ [ r x x r y x 0 r x y r y y 0 0 0 1 ] = [ 0 1 1 ] \begin{bmatrix} r_{yx}& r_{yy}& 1 \end{bmatrix} \cdot \begin{bmatrix} r_{xx}& r_{yx}& 0\\ r_{xy}& r_{yy}& 0\\ 0& 0& 1 \end{bmatrix} =\begin{bmatrix} 0& 1& 1 \end{bmatrix} [ryxryy1]⋅ rxxrxy0ryxryy0001 =[011]
代码
对于二维变换的代码相对来讲较麻烦一些,我不太喜欢OpenGL所带的矩阵运算操作,因此我自己写了一套简单的矩阵模版类。由于代码相对较长,我这里仅放出这几个变换的代码片段。
class Polygon
{
public:
Transform::Matrix<GLdouble> *vex;
Polygon(Pts vex)
{
this->vex = new Transform::Matrix<GLdouble>(vex.size(), 3, {{}}, 0);
for (int i = 0; i < vex.size(); i++)
{
(*this->vex)[i][0] = vex[i].x;
(*this->vex)[i][1] = vex[i].y;
(*this->vex)[i][2] = 1;
}
}
~Polygon()
{
delete vex;
}
Polygon *Translate(const Point &end)
{
vector<vector<GLdouble>> temp{{1, 0, 0}, {0, 1, 0}, {end.x, end.y, 1}};
Transform::Matrix<GLdouble> t(3, 3, temp);
(*vex) = (*vex) * t;
return this;
}
Polygon *Draw()
{
// cout << "Start" << endl;
glBegin(GL_POLYGON);
for (GLint i = 0; i < vex->CountRow(); i++)
{
// cout << i << ": " << (*vex)[i][0] << " " << (*vex)[i][1] << endl;
glVertex2d((*vex)[i][0], (*vex)[i][1]);
}
glEnd();
return this;
}
Polygon *Rotate(Point p, GLdouble radian)
{
Transform::Matrix<GLdouble> t1(3, 3, {{1, 0, 0}, {0, 1, 0}, {-p.x, -p.y, 1}});
Transform::Matrix<GLdouble> t2(3, 3, {{cos(radian), sin(radian), 0}, {-sin(radian), cos(radian), 0}, {0, 0, 1}});
Transform::Matrix<GLdouble> t3(3, 3, {{1, 0, 0}, {0, 1, 0}, {p.x, p.y, 1}});
(*vex) = (*vex) * t1 * t2 * t3;
return this;
}
Polygon *Scale(GLdouble x, GLdouble y)
{
if (x <= 0 || y <= 0)
{
cout << "WARNING: Invalid parameters" << endl;
return this;
}
Transform::Matrix<GLdouble> t(3, 3, {
{x, 0, 0},
{0, y, 0},
{0, 0, 1},
});
(*vex) = (*vex) * t;
return this;
}
Polygon *PointReflect(const Point &p)
{
Transform::Matrix<GLdouble> t1(3, 3, {{1, 0, 0}, {0, 1, 0}, {-p.x, -p.y, 1}});
Transform::Matrix<GLdouble> t2(3, 3, {
{-1, 0, 0},
{0, -1, 0},
{0, 0, 1},
});
Transform::Matrix<GLdouble> t3(3, 3, {{1, 0, 0}, {0, 1, 0}, {p.x, p.y, 1}});
*vex = (*vex) * t1 * t2 * t3;
return this;
}
Polygon *LineReflect(const Point &start, const Point &end, bool showAxis = false)
{
GLdouble x1 = start.x, x2 = end.x, y1 = start.y, y2 = end.y;
if (x1 > x2)
swap(x1, x2), swap(y1, y2);
if (showAxis)
{
glBegin(GL_LINES);
glVertex2d(x1, y1);
glVertex2d(x2, y2);
glEnd();
}
this->Translate({-x1, -y1});
GLdouble dy = y2 - y1;
GLdouble dx = x2 - x1;
if (dx == 0)
{
Transform::Matrix<GLdouble> t(3, 3, {{-1, 0, 0}, {0, 1, 0}, {0, 0, 1}});
*vex = (*vex) * t;
this->Translate({x1, y1});
return this;
}
GLdouble rad = atan(dy / dx);
if (rad < 0)
rad = 4 * atan(1) + rad;
this->Rotate({0, 0}, -rad);
Transform::Matrix<GLdouble> t1(3, 3, {{1, 0, 0}, {0, -1, 0}, {0, 0, 1}});
*vex = (*vex) * t1;
this->Rotate({0, 0}, rad);
this->Translate({x1, y1});
return this;
}
Polygon *Shear(const Point &sh)
{
Transform::Matrix<GLdouble> t1(3, 3, {{1, sh.y, 0}, {sh.x, 1, 0}, {0, 0, 1}});
*vex = (*vex) * t1;
return this;
}
};
完整代码请参考我的Github仓库: 2D变换-Github