关于37%法则的探究
前言
数学家欧拉发现了37%这个分界点,与大众来说应该毫无关系。可是现在越来越多人鼓吹用37%法则来进行选择,他们以为这是科学决策,其实只是对另一种未知事物的信仰。
我不否定37%法则的存在,也不推崇37%法则的运用。我只想通过这篇文章提高大众对37%法则的理解。
一、37%法则是什么?
1.故事导入
苏格拉底的3个弟子曾求教老师,怎样才能找到理想的伴侣。于是苏格拉底带领弟子们来到一片麦田,让他们每人在麦田中选摘一支最大的麦穗,要求是不能走回头路且只能摘一支。
第一个弟子刚刚走了几步便迫不及待地摘了一支自认为是最大的麦穗,结果发现后面的大麦穗多的是。
第二个弟子一直在寻找最大的麦穗,直到终点才发现前面最大的麦穗已经错过了。
第三个弟子把麦田分为三段,走过第一段麦田时,只观察,在心中把麦穗分为大、中、小三类;走过第二段时,还是只观察,验证第一段的判断是否正确;走到第三段,也就是最后三分之一时,摘下第一支他遇到的属于“大”类中的麦穗,然后走到终点。
2.问题提出
有一个列表,由n个随机分布的数字组成。从第一个数字开始,依次查看列表中的数字,并记录其大小。挑选一个正在查看的数字,已查看过的数字不能挑选。挑选完毕即停止查看列表数字。从什么时候挑选才能最大概率的挑中列表中的最大值?
3.问题抽象
可以建立一个挑选模型,分为观察阶段和选择阶段。
观察阶段:依次查看列表中前k个数字,并记录其大小,留意其中的最大值。
选择阶段:将前k个数字中的最大值与正在查看的数字作比较,如果遇到比它更大的数字就选择它。
这样,只需要求解出k为何值时,挑选出最大数字的概率最大,就可以知道答案了。
4.问题解答
对于某个固定的 k,如果最适合的数字出现在了第 i 个位置,此时挑选出最大值的概率记作P(k)。计算公式如下:
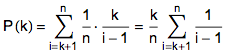
其中1/n是最适合的数字出现在第i个位置的概率,k/(i-1)表示k到i之间的数字比前k个数字都小的概率。只有满足上述两个条件才能挑出适合的数,因此这两个概率相乘。只有i>k,才有可能在第k个数字之后挑选出最大的数字。将i出现在k到n的情况进行概率累加,就是参考位置为k时挑选最适合数字的概率。
用 x 来表示 k/n 的值,并且假设 n 充分大,则上述公式可以写成:
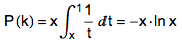
对 -x · ln x 求导,并令这个导数为 0,可以解出 x 的最优值—— 1/e 。
1/e 大约等于 0.37(e ≈2.718281828459)。因此列表前37%的数字作为参考,如果遇到比这些数字还大的,就选择它。这样挑选出最大数字的概率最大。
二、用python代码模拟
1.设计思路
通过python代码,我们可以模拟非常非常多次决策过程。
令k为前1%,进行上万次结果模拟,并记录其每次选择的结果。
令k为前2%,进行上万次结果模拟,并记录其每次选择的结果。
令k为前3%,进行上万次结果模拟,并记录其每次选择的结果。
……
令k为前99%,进行上万次结果模拟,并记录其每次选择的结果。
我们只需要比较,挑选出最大值的结果个数,就可以得知k为多少合适。
为了完成上面的过程,需要拆分成三个步骤。
第一个步骤:生成一个随机数列表,作为筛选对象。
第二个步骤:用for循环实现k从1到99对随机数列表的挑选过程,并把每个k挑选出的数字放入对应的列表中。
第三个步骤:对第一个步骤和第二个步骤重复执行上万次,得到k=1至k=99对应的99个挑选结果列表。并统计每个列表里有多少个属于筛选数列的最大值,将最大值最多的列表对应的k值输出。
2.生成随机数列表
生成含有100个随机数的列表,作为模拟挑选对象。
代码如下:
import random #引入随机模块
def text():#定义生成随机数字列表的函数
global li #将列表设置为全局变量,方便后续使用
li = [] #创建空列表作为容器
for i in range (100): #将下面的步骤重复一百遍
a = random.randint(0,100) #令a为0至100的一个随机数
li.append(a) #将a添加到列表中
pass3.模拟挑选过程
这一块的设计需要更多思考,代码核心就在此处。
前面虽然说“令k为前1%,进行上万次结果模拟,并记录其每次选择的结果”,但实际上我们的操作顺序并不是这样。我们并没有生成99个上万次的筛选列表,而是生成一个列表让k从1执行到99,再生成一个列表让k从1执行到99,直到生成上万个筛选列表。这样一个列表用99次,就可以大大节约运行内存了,并且代码也比较好写。
每个k值都表示将前k%的数字拿来作为参考,去挑选更大的数字。这样k从1到99,我们需要99个不同的列表来接收不同k值每次进行的挑选结果。你不可能用手把这99个列表一个个敲出来吧?所以我们需要自动生成99个接收列表。点这里:动态生成变量名方法
我们有了挑选结果,但如何知道挑选结果有多好呢?只要把我们生成的上万个供筛选的列表进行统计,得到平均最大值、平均最小值、平均的平均值,就可以知道了。
代码如下:
def select (x): #定义模拟挑选函数,x为每个k的挑选次数
global limax ,limin ,liaver ,prepare_list #将列表最大值、最小值、平均值以及结果容器设为全局变量,方便后面函数外使用
limax=[] #生成一个列表,用来装生成的上万个数列的最大值
limin=[] #生成一个列表,用来装生成的上万个数列的最小值
liaver=[] #生成一个列表,用来装生成的上万个数列的平均值
prepare_list = locals() #准备locals函数,locals()函数会以字典类型返回当前位置的全部局部变量
for i in range(100): #让i从0遍历到99
prepare_list['list_' + str(i+1)] = [] #让字典key为list_i+1,value为列表
pass
for item in range(x): #让item遍历x次
text() #生成供挑选的数列
limax.append(max(li)) #将数列的最大值装入列表
limin.append(min(li)) #将数列的最小值装入列表
liaver.append(sum(li)/len(li)) #将数列的平均值装入列表
for i in range(100): #让i遍历100次
k=0 #令k等于0
le = [] #生成一个空列表,用来装供筛选数列的前k个数作为参考数列
for one in li: #遍历供筛选数列,用来制作参考数列
k += 1 #令k加1
le.append(one) #将遍历的数添加到le列表里
if k >i:
c = max(le) #如果k大于i,就挑选出参考数列的最大值赋予c
break #只要k大于i就跳出制作参考数列的循环,i是0到99,k要执行1到100
for two in li[k:]: #遍历供筛选数列第k个之后的数
if two > c or two == li[99]:#如果有大于c的数或遍历到最后一个数
prepare_list['list_' + str(i+1)].append(two)#将筛选结果添加到对应列表中
break #跳出循环,继续执行
else:
pass
pass3.输出结果
前面把挑选过程模拟完了,现在到了结果输出阶段。
每个不同的k都代表着不同的策略,我们需要对每个策略得到的结果进行总结。所以需要输出不同策略下,挑选结果的平均值和挑选出最大值的次数。我们还需要筛选出其中挑选平均值最大的策略和挑选出最大值最多的策略。
我们生成的供挑选数列有上万个,需要对其进行一个整体了解。输出这上万个数列的最大值平均数、最小值平均数、平均值的平均数。
代码如下:
def out():
ls = {} #生成接收筛选结果平均值的字典
dg = {} #生成接收筛选最大值次数的字典
for i in range(100): #重复一百遍
if len(prepare_list[f'list_{i+1}'])==0: #如果得到筛选结果的列表为空
print(f"只参考前{i+1}个",end="") #显示k的位置
print("没有平均值,因为全错过了!\n") #列表为空即没有挑选出一个数字
pass
else:
average = sum(prepare_list[f'list_{i+1}'])/len(prepare_list[f'list_{i+1}']) #计算平均值,列表数字总和除以列表数字个数
average = round(average,4) #平均值保留四位小数
ls[f'{i+1}'] = average #将平均值填入字典对应key的value值,表示采用对应k策略获得的平均值
g = 0 #定义变量g,用来确定供筛选数列最大值的位置,即确定生成的是第几个供筛选数列的最大值。
count = 0 #定义变量count,用来计算挑选出最大值的次数。
for item in prepare_list[f'list_{i+1}']: #遍历挑选结果列表里的数字
if item == limax[g]: #将挑选出的数字与对应数列最大值进行比较
count+=1 #如果挑选出的数字是该数列的最大值,则计数加一
pass
g += 1 #进行第下一个数列的确定
pass
print(f"只参考前{i+1}个\t选了{len(prepare_list[f'list_{i+1}'])}次\t挑选结果平均值为{average}\t选出最大值的次数为{count}次,") #遍历完成,输出参考个数、挑选次数、挑选结果平均值、选出最大值的次数,用制表符\t来分隔开
dg[f'{i+1}']= count #记录每个策略收集最大值的次数
print("列表平均最大值为:",end="")
print(sum(limax)/len(limax)) #输出供筛选数列的最大值
print("列表平均最小值为:",end="")
print(sum(limin)/len(limin)) #输出供筛选数列的最小值
print("列表平均值的平均值为:",end="")
print(round(sum(liaver)/len(liaver),4)) #输出供筛选数列的平均值
ls_key = max(ls,key=ls.get) #ls_key表示筛选结果中平均值最大的策略
ls_value = ls[max(ls,key=ls.get)] #ls_value表示其平均值
print(f'最优参考个数为{ls_key}个,平均值为{ls_value}') #输出结果
dg_key = max(dg,key=dg.get) #dg_key表示筛选结果中挑选出最大值最多的策略
dg_value = dg[max(dg,key=dg.get)] #dg_value表示其挑出最大值的个数
print(f'参考个数为{dg_key}个时,挑出最优个数最多,挑了{dg_value}个') #输出结果
pass4.开始执行
三个步骤都用函数定义好了,最后只需要依次执行就好了。
代码如下:
def main():
select(10000)
out()
if __name__ == '__main__':
main()预备~执行!
然后盯着这黑屏看了一个世纪,要不是电脑风扇在转着,任务管理器显示正在运行,很难不怀疑死机了。这怎么忍得了,赶紧加一个进度条吧。在for i in range(100):上面加上z=0,在for item in range(x): 下面加上这些代码,就可以显示已完成百分之几啦。
代码如下:
if item == z*x/100:
print(f"已完成{z}%")
z += 1
pass再执行一遍。
可以看到有不断更新进度,让等待不再崩溃。
三、生成的随机列表问题
1.问题发现
代码运行完成后的结果如下图。可以看到运行的代码在K为27时挑选的最优个数最多,这与上述计算得出的37%不符。考虑到37%法则人尽皆知,这肯定是代码出现了问题。
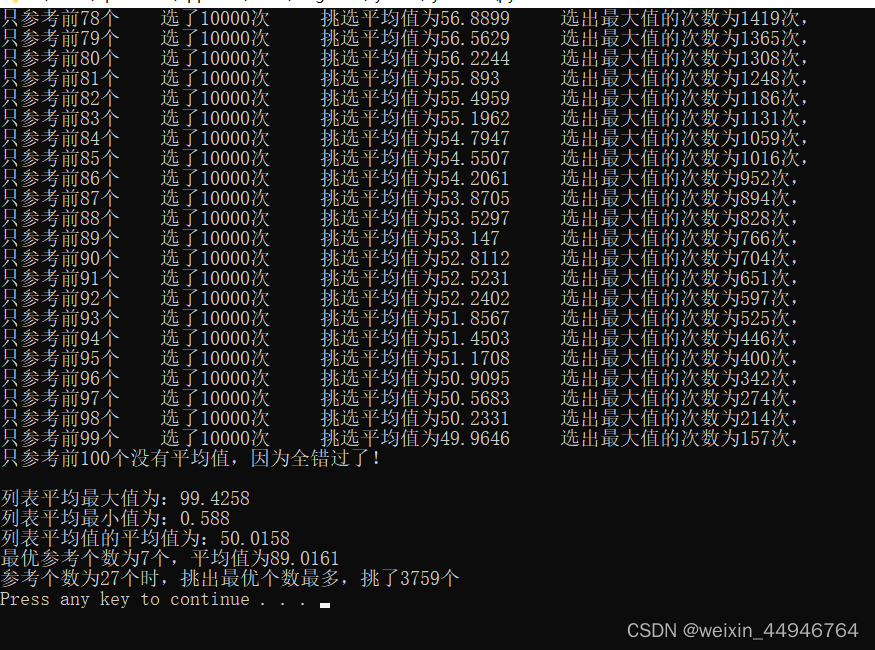
检查了挑选过程的代码,发现没有问题。于是利用random.normalvariate函数生成了一个均值为50的正态分布列表,列表里一共一百个元素。试一试从这个列表抽取结果如何。
代码如下:
def text():#生成正态分布的随机数列
global li
li = []
for i in range (100):
a = random.normalvariate(50, 20)
a = round(a)#去除多余小数
li.append(a)注释掉之前的随机数列生成函数后运行一下,结果很神奇,居然正好是37。
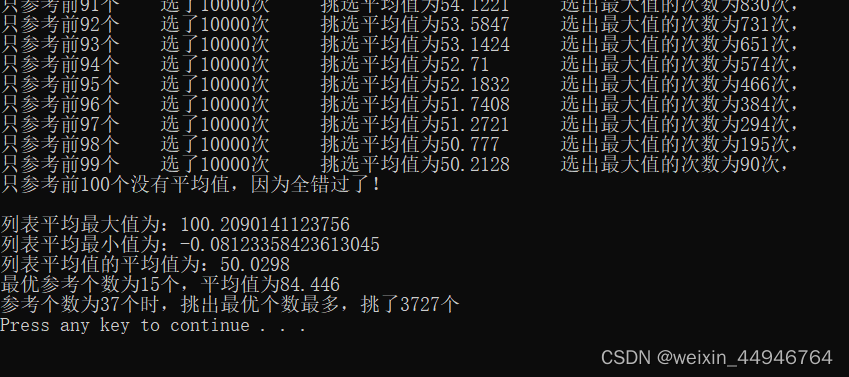
可以看到生成的这个正态分布数列最大值是100,最小值是0,平均值是50,和之前用random.randint函数生成的数列几乎一样,但结果却变正常了。难道37%法则仅适用于正态分布的随机数吗?
2.其他随机列表的生成方式
为了研究这个问题,应该再次生成一个随机列表。这次利用random.shuffle函数将含有0到100的列表元素顺序打乱。
代码如下:
def text():
global li
li = []
for i in range(1,101):
li.append(i)
random.shuffle(li)先将0到100按顺序装填到列表中,再用shuffle打乱,这样就得到了一个一百以内的随机数列表。运行一下,看看结果。
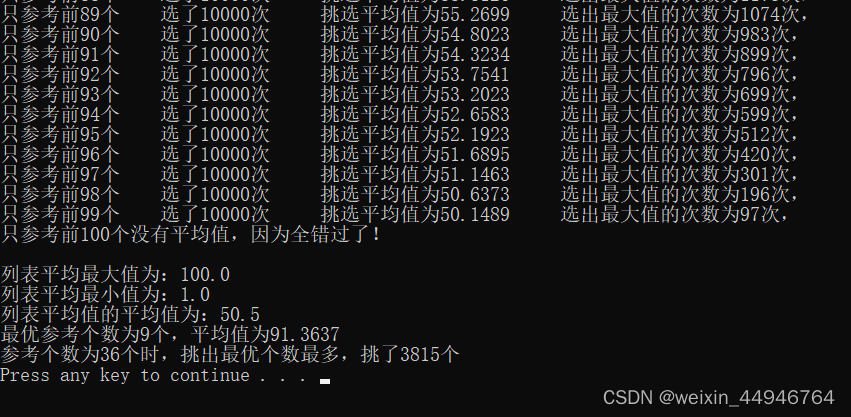
可以看到,出现的是36,离37很近,多次运行后也是在这附近。这说明37%法则并不是非得正态分布情况下才适用。问题应该处在random.randint生成的数列上。考虑到该方法生成的数列内每个元素都是从0到100之间随机生成,数列本身并不一定包含0到100中的每个数字。这种方式产生的数是否分布不均匀?比如生成小数字的可能性更大?
3.列表元素偏态与均匀分布的探究
为了验证这些随机生成的列表内元素是否均匀分布,可以统计生成的列表最大值或最小值的平均位置在哪。如果是均匀分布的,这个值必定在50附近。因为每个列表有100个数,位置是从0到100,如果每个元素都均匀分布那最大值出现在第一个的概率和出现在第一百个的概率一样,所有位置的平均值一定是50。但这个值是50也不代表一定是均匀分布,比如均值是50的正态分布,该代码核心功能应该是判断生成的列表是否偏态。这个代码不能断定列表是否均匀分布,但可以通过判断列表元素分布是偏态,来否定列表是均匀分布。
代码如下:
def indexmax(x):
sdf=[]
sumlimax = 0
for i in range(0,x):
text()
sdf.append(li.index(min(li)))
sumlimax += li.index(min(li))
print(li.index(max(li)))
print(f'生成了{x}个列表,最大值的平均位置在{sumlimax/x+1}个(从1开始数)')利用这个函数,分别测试上述三种方法生成的数列是否偏态。
首先测试random.normalvariate函数生成的正态分布列表。结果如下:

最大值的平均位置在50左右,没什么好意外的,毕竟这个数列是均值为50生成的随机正态数列。这说明上面的代码没有问题。
再测试一下random.shuffle函数生产的数列是否偏态。结果如下
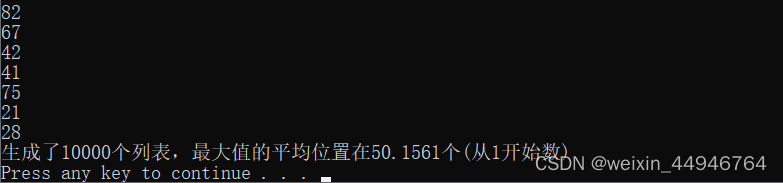
最大值的平均位置也在50左右,这说明random.shuffle生成的数列并没有偏态,极大可能是均匀分布。
最后再测试一下random.randint生产的函数,结果如下。

可以看到,最大值的平均位置在42,该方法生成的列表在之前执行时最大值是100,最小值是0,平均值是50。而现在发现最大值的平均位置在第42位,这说明该列表并不是均匀分布的。
为什么random.randint生成的列表是偏态的?
推测一:此方法生成的随机数并不涵盖所有1到100的数,是由于有些数字少了有些数字重复,才导致的偏态分布。作用机理暂且不明,数学不是很好。
推测二:是random伪随机导致的这个结果。网上有一些说法,不过个人感觉这个可能性不大。
四、关于37%法则的更多细节
1.什么情况?
在代码的世界里,随机数列就是背景环境。每一个数列都无序混乱,每一次选择都无限可能。在一次次的不断尝试之下,数列有了规律,好像结果也有了趋向。
但是随机并不随机,随机数产生的规律并不适用所有随机情况。就像上面random.randint生成的数列一样,也是随机的,但产生不了37%的结果。在生活中,我们真能判断是哪种情况吗?我们甚至连这串列表的长度都无法确定。
2.何为最优解?
37%法则里提到的这个数字,是挑选出最大数的最佳策略,并不代表这种方法挑选出来的平均值最大。那么,等待那最好的还是选择最稳妥的?
上面代码运行结果里写的最优参考个数,就是均值最大的参考个数。不同方式生成的随机数列产生的最优参考个数也不一样,但都比37%法则更靠前。这意味着选择了最好的就得放弃最稳妥的。
总结
37%法则无法解决生活中的选择问题,因为所有选择都必须自己亲自做。