【数据结构】栈和队列
一、栈
1.栈的概念与结构
栈是一种特殊的线性表,即栈也是线性表,可见栈的特性,栈只运行在特定的一端进行插入和删除操作,这一端我们就叫为栈顶,另一端我们称为栈底,所以栈有一个很重要的性质,即所有入栈的元素都遵循后进先出LIFO(last in first out)的原则。
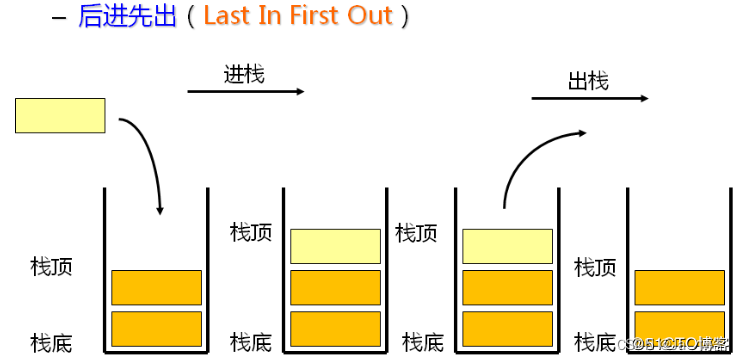
2.栈的具体实现
栈的实现有两种实现方式,一种是链表,一种是顺序表,如果是链表的话也是可以实现的,我们知道单链表的尾插是需要遍历链表找到尾才可以尾插,故代价比较大,而顺序表的数组就相对代价小了很多,所以我们的栈是用顺序表实现的。
下面贴上栈的具体实现代码:
Stack.h --- 实现栈的函数的声明,类型的定义等等
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top; // 栈顶
int capacity; // 容量
}ST;
// 初始化栈
void STInit(ST* ps);
// 入栈
void STPush(ST* ps, STDataType data);
// 出栈
void STPop(ST* ps);
// 获取栈顶元素
STDataType STTop(ST* ps);
// 获取栈中有效元素个数
int STSize(ST* ps);
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
bool STEmpty(ST* ps);
// 销毁栈
void STDestroy(ST* ps);
Stack.c --- 栈的函数接口实现
#define _CRT_SECURE_NO_WARNINGS 1
#include"Stack.h"
void STInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->top = 0;
ps->capacity = 0;
}
void STPush(ST* ps, STDataType data)
{
assert(ps);
if (ps->top == ps->capacity)
{
int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);
if (tmp == NULL)
{
perror("realloc fail");
return;
}
ps->a = tmp;
ps->capacity = newcapacity;
}
ps->a[ps->top] = data;
ps->top++;
}
void STPop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}
STDataType STTop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->a[ps->top - 1];
}
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
void STDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->capacity = ps->top = 0;
}
二、队列
1.队列的概念与结构
队列是一种在特定一端进行插入数据,另一端进行删除数据,分别为队列的入队和出队,
队列具有先进先出FIFO(first in first out)的特性。
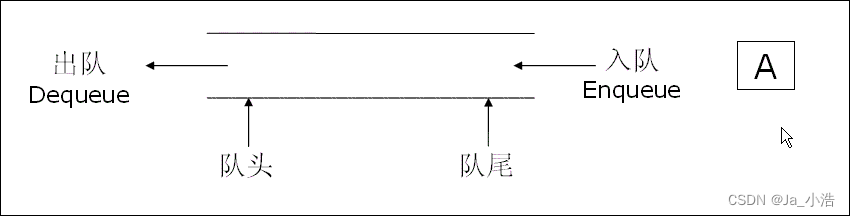
2.队列的具体实现
队列可以用链表和顺序表实现,但我们通常是使用链表实现,因为我们在数组头上入数据时需要进行大量的挪动数据,时间复杂度高,效率低,而链表的头插就会很方便,所以我们选用链表作为链表的实现方式。
Queue.h --- 队列的函数的声明与类型的定义。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* next;
QDataType data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* phead;
QNode* ptail;
int size;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);
Queue.c --- 函数接口的实现
#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"
void QueueInit(Queue* q)
{
assert(q);
q->phead = q->ptail = NULL;
q->size = 0;
}
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
return;
}
newnode->data = data;
newnode->next = NULL;
if (q->ptail == NULL)
{
q->phead = q->ptail = newnode;
}
else
{
q->ptail->next = newnode;
q->ptail = newnode;
}
q->size++;
}
void QueuePop(Queue* q)
{
assert(q);
assert(q->phead);
QNode* del = q->phead;
q->phead = q->phead->next;
free(del);
del = NULL;
if (q->phead == NULL)
q->ptail = NULL;
q->size--;
}
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->phead;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
q->phead = q->ptail = NULL;
q->size = 0;
}
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->phead);
return q->phead->data;
}
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->ptail);
return q->ptail->data;
}
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}
bool QueueEmpty(Queue* q)
{
assert(q);
return q->phead == NULL;
}3.循环队列
队列还有一种特殊的队列,这种队列就是循环队列。
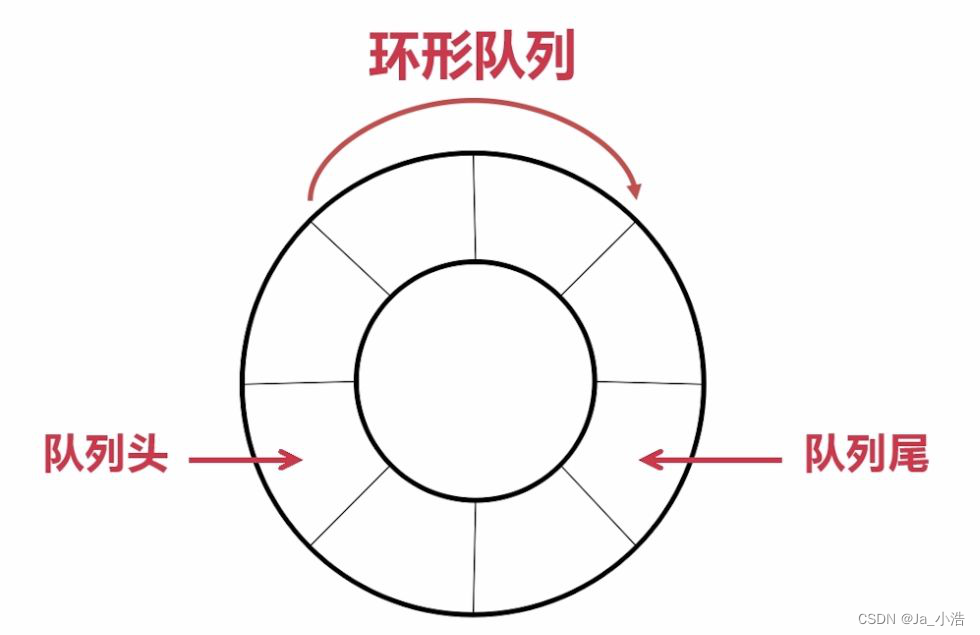
对于循环队列的实现我们主要是弄懂空和满是如何判断的,这样我们就很容易就能写出一个循环队列。
循环队列也是可以用链表和顺序表实现,但建议使用用顺序表实现,链表实现更不利于控制,具体小伙伴们可以尝试一下链表实现,可能会很痛苦哦!
如果是用顺序表实现,如何判断空呢?
如果我们申请k个空间存放k个数据。
我们会学到用头与尾相等就可以了,但如何判断满呢?
我们第一想法可能是头front在下标0的位置,尾rear在下标为k-1的位置,这样想,那可就太天真了。事实是front是不一定就是在下标为0的位置的,可能在其他的任何位置,那就很难判满了。
由以上发现循环队列不像我们想的这么简单的,如果我们想它既能判空又能判满,那就必须再想一个方法,使判空和判满能互不干扰,一劳永逸。
这里我们提供一个方法就是可以我们多申请一个额外空间,即申请k+1个空间,这样有了额外一个空间,判空依旧可以是front == rear 而判满就可以是 front == (rear + 1) % k + 1。
下面有三个oj题,小伙伴们可以进行练习。