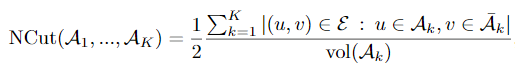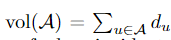阅读笔记Graph Representation Learning–Chapter2
系列文章目录
阅读笔记Graph Representation Learning–Chapter2
阅读笔记Graph Representation Learning–Chapter3
阅读笔记Graph Representation Learning–Chapter4
阅读笔记Graph Representation Learning–Chapter5
阅读笔记Graph Representation Learning–Chapter6
阅读笔记Graph Representation Learning–Chapter8
文章目录
2.1 GRAPH STATISTICS AND KERNEL METHODS
2.1.1 Node-level statistics and features
(1)Node degree
一个节点所包含的边的数量称为这个节点的度(degree)
(2)Node centrality
节点度只是衡量一个节点有多少个邻居,但这并不一定足以衡量图中一个节点的重要性
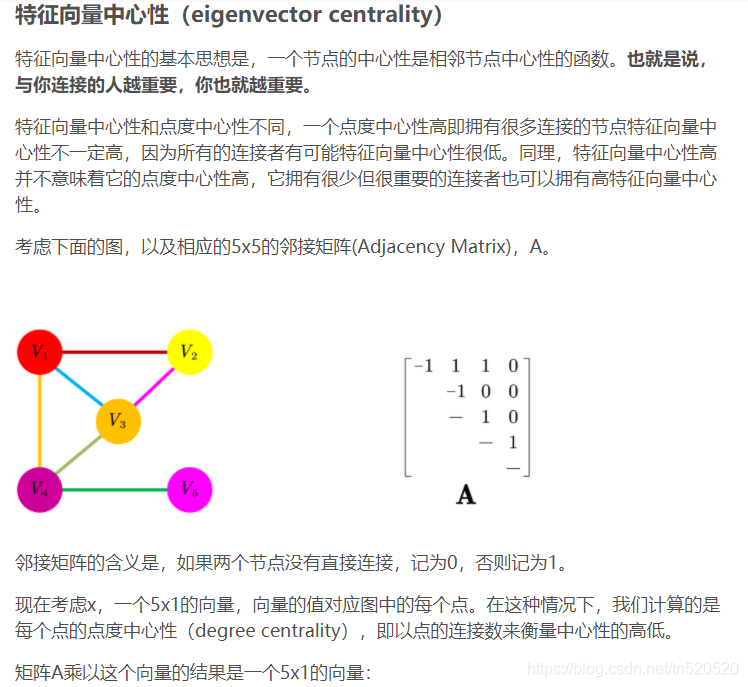
eigenvector centrality
度只是衡量每个节点有多少个邻居,而特征向量中心性还考虑了一个节点的邻居有多重要。我们通过递推关系定义节点的特征向量中心性,其中节点的中心性与相邻节点的平均中心性成比例。
实际上是求一个向量e,满足 λe=Ae。λ是一个常值,取邻接矩阵A的最大特征值。
解释如下(来源于link1):


betweenness centrality
测量一个节点位于其他两个节点之间的最短路径上的频率.如果一个成员位于其他成员的多条最短路径上,那么该成员就是核心成员,就具有较大的中介中心性
closeness centrality
测量一个节点和所有其他节点之间的平均最短路径长度。如果节点到图中其他节点的最短距离都很小,那么它的接近中心性就很高。相比中介中心性,接近中心性更接近几何上的中心位置。
(3)The clustering coefficient(聚集系数)
一个节点的聚类参数被称为 Local Cluster Coefficient。它的计算方法也是非常的简单粗暴。先计算所有与当前节点连接的节点中间可能构成的 link 有多少个,这个数会作为分母,然后计算实际上有多少个节点被连接上了,这个数会作为分子。最终的计算结果就是 Local Cluster Coefficient。聚类系数之所以叫聚类系数,是因为它测量的是一个节点的邻域聚类有多紧密。当聚类系数为1时,表示u的所有邻居也是彼此的邻居。

第二种方法是先计算在图中已经关闭上的三角形的个数,除上没有闭上的三角形的个数。这种计算方法叫做 Transitivity。
2.1.2 Graph-level features and graph kernels
(1)Bag of nodes
定义图级特征的最简单方法是聚合节点级统计信息。例如,可以基于图中节点的程度,中心性和聚类系数来计算直方图或其他汇总统计信息。然后可以将这些聚合的信息用作图级表示。这种方法的缺点是,它完全基于局部节点级信息,可能会错过图中重要的全局属性。
(2)The Weisfieler-Lehman kernel
一种改进基本节点袋方法的方法是使用迭代邻域聚合策略。这些方法的想法是提取节点级特征,这些节点级特征不仅包含其局部自我图的特征,而且还包含更多信息,然后将这些更丰富的特征聚合到图级表示中。这些策略中最重要,最著名的也许是WL算法。WL算法背后的基本思想如下:
- 首先,给每一个节点分配一个初始的标签。在大多数图中,这些标签就是每个节点的度。
- 接下来,我们通过对节点邻域内的当前标签的多集进行哈希,迭代地为每个节点分配一个新标签。
- 重复执行步骤2,现在对于总结其K跳邻域结构的每个节点我们都有了一个标签。然后,我们可以计算这些标签上的直方图或其他汇总统计信息,作为图的特征表示。换句话说,WL核是通过测量两个图的合成标签集之间的差来计算的。
WL内核是流行的,经过深入研究的并且具有重要的理论特性。 例如,一种流行的近似图同构的方法是检查WL算法经过K回合后,两个图是否具有相同的标签集,并且这种方法已知可以解决大量图的同构问题。
(3)Graphlets and path-based methods
最后,正如我们对节点级特性的讨论一样,在图上定义特性的一个有效而强大的策略是简单地计算不同小子图结构(在此上下文中通常称为graphlets)的出现次数。在形式上,graphlet内核涉及枚举特定大小的所有可能的图形结构,并计算它们在整个图形中出现的次数。这种方法的挑战在于,尽管已经提出了许多近似方法,但对这些图进行计数是一个组合困难的问题.枚举所有可能的图形的另一种方法是使用基于路径的方法。在这些方法中,不必枚举图,而是简单地检查图中出现的不同类型的路径。
graphlet:连通的非同构子图
同构图:如果能够通过重新标记图G的顶点而产生图H,则称两个图G和H是同构图
可以理解为两个图之间存在双向映射
如果两个图是同构的,不取决于两个图是怎么画的,也不取决于如何标记顶点。
图G和H是同构的,那么它们的阶相同,大小相同,各顶点度数也对应相同
可以理解edges是具有弹性的绳子,同构表示,节点固定,对G“扯一扯”绳子即可变换成H。
2.2 Neighborhood Overlap Detection
在2.1中,我们介绍了各种方法来提取有关单个节点或整个图的特征或统计信息。这些节点和图形级统计信息对于许多分类任务很有用。 但是,它们的局限性在于它们无法量化节点之间的关系。例如,上一节讨论的统计数据对于关系预测任务不是很有用,因为我们的目标是预测两个节点之间的边的存在。在本节中,我们将考虑对节点之间的邻域重叠的各种统计度量,这些度量量化了对节点之间的关联程度。例如,最简单的邻域重叠度量仅计算两个节点共享的邻居数:
S[u,v] =|N(u)∩N(v)|
S[u,v]:表示量化节点u和v之间关系的值;
S∈R |V|×|V|:表示汇总所有成对节点统计信息的相似矩阵。
即使本节中讨论的任何统计量都没有涉及“机器学习”,但它们仍然是关系预测的非常有用且功能强大的基准。节点u 与 节点v之间相互连接的概率和他们的邻域重叠统计值S[u,v] 成正比。
P(A[u,v] = 1)∝S[u,v]
因此,为了使用邻域重叠度量来接近关系预测任务,只需设置一个阈值即可确定何时预测边缘的存在。请注意,在关系预测设定中,我们通常假设我们只知道真实边的子集。我们希望在训练边缘上计算出的节点-节点相似性度量能够准确地预测测试集中边的存在性的大小。
2.2.1 Local overlap measures
局部重叠统计只是两个节点共享的公共邻居数量的函数。
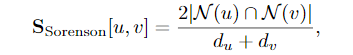
正则化通常是非常重要的;否则,重叠测度会对节点数量较大的节点的预测边缘产生较大的偏差。其他类似的方法包括索尔顿指数,它通过u和v的乘积正常化。
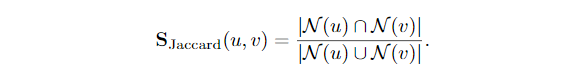
以及Jaccard overlap:
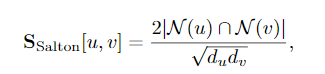
通常,这些措施旨在量化节点邻域之间的重叠,同时最大程度地减少由于节点度引起的偏差。除了简单地计算共同邻居的数量外,还有一些措施试图以某种方式考虑共同邻居的重要性。
资源分配(RA)指标计算公共邻居的反比度
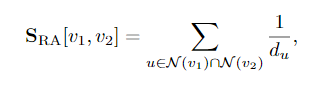
the Adamic-Adar (AA) index:

2.2.2 Global overlap measures
局部重叠度量对于链路预测是非常有效的启发式方法,即使与先进的深度学习方法相比,也常常获得具有竞争力的性能。但是,局部方法的局限性在于它们仅考虑局部节点邻域。 例如,两个节点在其邻域中可能没有局部重叠,但仍是图中同一社区的成员。全局重叠统计数据试图将这种关系考虑在内。
Katz index
Katz index可以区分不同的邻居节点不同的影响力。Katz index给邻居节点赋予不同的权重,对于短路径赋予较大的权重,而长路径赋予较小的权重。
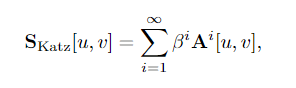
β 为权重衰减因子,为了保证数列的收敛性, β 的取值须小 于邻接矩阵 A 最大特征值的倒数。

图片来源:link1
Leicht, Holme, and Newman (LHN) similarity
未完待续
2.3 Graph Laplacians and Spectral Methods
在讨论了用图数据进行分类的传统方法以及传统的关系预测方法之后,我们现在转向学习在图中聚类节点的问题。。
2.3.1 Graph Laplacians
Unnormalized Laplacian
**L=D−A**
A:邻接矩阵
D:度矩阵
示例:pandas 是基于NumPy 的一种工具,该工具是为了解决数据分析任务而创建的。
Normalized Laplacians
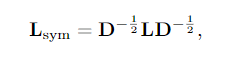
random walk Laplacian
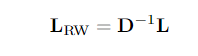
2.3.2 Graph Cuts and Clustering
Graph Cuts
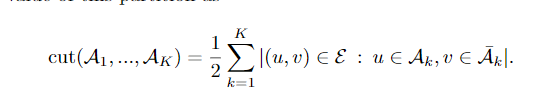
换言之,切割只是计算有多少条边穿过节点划分之间的边界。现在,将节点定义为K个群集的最佳群集的一种方法是选择一个最小化该割值的分区。有一些有效的算法可以解决这个任务,但是这种方法的一个已知问题是,它倾向于使集群只包含一个节点。因此,我们通常不是简单地最小化切割,而是寻求最小化切割,同时保证分区都是合理的大。一种流行的执行方法是最小化Ratio Cut。
RatioCut切图为了避免最小切图,对每个切图,不光考虑最小化cut(A1,A2,…Ak),它还同时考虑最大化每个子图点的个数,
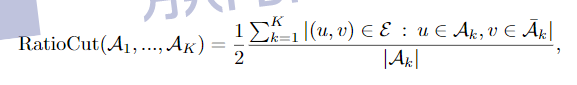
Normalized Cut (NCut):
Ncut切图和RatioCut切图很类似,但是把Ratiocut的分母|Ai|换成vol(Ai). 由于子图样本的个数多并不一定权重就大,我们切图时基于权重也更合我们的目标,因此一般来说Ncut切图优于RatioCut切图。