处理字符串公式转换为数学公式计算得到结果---无任何依赖版本----使用栈完成
处理字符串公式转换为数学公式计算得到结果:
如何将字符串转换为数学公式?
1. 需要引入依赖
-
**JEP (Java Math Expression Parser)**库:EP 是一个功能强大的Java库,用于解析和计算数学表达式。它支持变量、函数、常量等,并且可以处理各种数学运算。你可以通过 JEP 将字符串转换为数学表达式,然后计算其值。
import org.lsmp.djep.djep.DJep; import org.nfunk.jep.Node; public class MathParser { public static void main(String[] args) throws Exception { DJep jep = new DJep(); jep.addStandardFunctions(); jep.addStandardConstants(); jep.addVariable("x", 10.0); // 设置变量的值 String expression = "2*x + sin(x)"; Node node = jep.parse(expression); double result = (Double)jep.evaluate(node); System.out.println("Result: " + result); } } -
Apache Commons Math:Apache Commons Math库也提供了一些数学表达式解析的功能。它支持不同的数学函数和运算,可以将字符串转换为数学表达式并进行计算。
Apache Commons Math库的使用示例:
import org.apache.commons.math3.analysis.function.Sin; import org.apache.commons.math3.analysis.function.Add; public class MathParser { public static void main(String[] args) { String expression = "2*x + sin(x)"; Add function = new Add(new Mult(2.0, new Identity()), new Sin()); UnivariateFunction ufunc = function.compile(expression); double result = ufunc.value(10.0); System.out.println("Result: " + result); } } -
还有javaScript库等一些方法,但是这些都需要引入依赖。
2. 无需引入依赖,可匹配例如-0.00000057e-12*tilt*tilt+0.00178274*tilt+0.95884259的公式
整个代码为:
public static BigDecimal calculate(String formula, BigDecimal tilt) {
//先将科学计数法转换为非科学计数法:
formula = convertToPlainFormula(formula);
// 去掉空格, 替换公式中的 "tilt"
formula = formula.replaceAll(" ", "").replaceAll("tilt", tilt.toString());
String[] tokens = formula.split("(?<=[-+*/])|(?=[-+*/])");
Stack<BigDecimal> numbers = new Stack<>();
Stack<Character> operators = new Stack<>();
boolean isNegative = false; // 用于处理负数开头的情况
for (String token : tokens) {
if (token.matches("[+\\-*/]")) {
if (token.equals("-")) {
if (isNegative) {
isNegative = false;
BigDecimal number = numbers.pop();
numbers.push(number.negate()); // 处理负数开头的情况
} else {
isNegative = true;
}
} else {
char operator = token.charAt(0);
while (!operators.isEmpty() && hasPrecedence(operator, operators.peek())) {
BigDecimal b = numbers.pop();
BigDecimal a = numbers.pop();
char op = operators.pop();
BigDecimal result = performOperation(a, b, op);
numbers.push(result);
}
operators.push(operator);
}
} else {
BigDecimal number = new BigDecimal(token);
if (isNegative) {
number = number.negate();
isNegative = false;
}
numbers.push(number);
}
}
while (!operators.isEmpty()) {
BigDecimal b = numbers.pop();
BigDecimal a = numbers.pop();
char op = operators.pop();
BigDecimal result = performOperation(a, b, op);
numbers.push(result);
}
return numbers.pop();
}
@NotNull
private static String convertToPlainFormula(String formula) {
// 使用正则表达式匹配科学计数法表示的数字
Pattern pattern = Pattern.compile("([+-]?\\d*\\.?\\d*[eE][+-]?\\d+)");
Matcher matcher = pattern.matcher(formula);
// 逐个替换匹配到的科学计数法表示
while (matcher.find()) {
String match = matcher.group();
BigDecimal number = new BigDecimal(match);
String plainString = number.toPlainString();
formula = formula.replace(match, plainString);
}
return formula;
}
private static boolean hasPrecedence(char operator1, char operator2) {
return (operator2 == '*' || operator2 == '/') && (operator1 == '+' || operator1 == '-');
}
private static BigDecimal performOperation(BigDecimal a, BigDecimal b, char operator) {
switch (operator) {
case '+':
return a.add(b);
case '-':
return a.subtract(b);
case '*':
return a.multiply(b);
case '/':
return a.divide(b, 8, BigDecimal.ROUND_HALF_UP); // 保留8位小数并四舍五入
default:
throw new IllegalArgumentException("Unsupported operator: " + operator);
}
}
可使用如下来测试:
public static void main(String[] args) {
System.out.println(calculate("-0.00000057e-12*tilt*tilt+0.00178274*tilt+0.95884259", BigDecimal.valueOf(45.34)));
System.out.println(-0.00000057e-12 * 45.34 * 45.34 + 0.00178274 * 45.34 + 0.95884259);
}
3. 结果显示,计算是正确的:
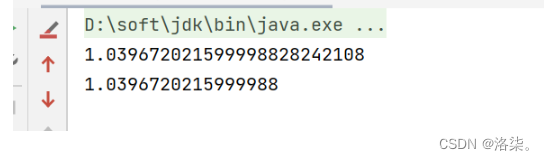
4. 代码解释:
这段代码是一个Java方法,名为 calculate,用于解析并计算一个数学表达式的结果。让我逐行解释它:
javaCopy code
public static BigDecimal calculate(String formula, BigDecimal tilt) {
这是一个公共静态方法的声明。它接受两个参数:一个是字符串 formula,表示数学表达式,另一个是 BigDecimal 类型的 tilt,用于替换表达式中的 “tilt”。
javaCopy code // 去掉空格, 替换公式中的 "tilt"
formula = formula.replaceAll(" ", "").replaceAll("tilt", tilt.toString());
这两行代码将表达式中的空格去掉,并将所有的 “tilt” 替换为 tilt 参数的字符串表示。
javaCopy code
String[] tokens = formula.split("(?<=[-+*/])|(?=[-+*/])");
这行代码将表达式拆分成一个字符串数组 tokens,使用正则表达式 (?<=[-+*/])|(?=[-+*/]) 作为分隔符,这个正则表达式的意思是在运算符前后进行拆分。
javaCopy code Stack<BigDecimal> numbers = new Stack<>();
Stack<Character> operators = new Stack<>();
这两行代码创建了两个栈,一个用于存储数字,另一个用于存储运算符。
javaCopy code
boolean isNegative = false; // 用于处理负数开头的情况
这行代码声明一个布尔变量 isNegative,用于跟踪是否遇到负数。
javaCopy code
for (String token : tokens) {
这是一个循环,遍历拆分后的表达式中的每个 token。
javaCopy code
if (token.matches("[+\\-*/]")) {
这行代码检查 token 是否是一个运算符(+、-、*、/)。
javaCopy code if (token.equals("-")) {
if (isNegative) {
isNegative = false;
BigDecimal number = numbers.pop();
numbers.push(number.negate()); // 处理负数开头的情况
} else {
isNegative = true;
}
}
这段代码处理负数的情况。如果 token 是负号 -,并且 isNegative 为真,那么从栈中弹出一个数,取其相反数,然后将结果推回栈中。否则,将 isNegative 设置为真,表示接下来的数是负数。
javaCopy code } else {
char operator = token.charAt(0);
while (!operators.isEmpty() && hasPrecedence(operator, operators.peek())) {
BigDecimal b = numbers.pop();
BigDecimal a = numbers.pop();
char op = operators.pop();
BigDecimal result = performOperation(a, b, op);
numbers.push(result);
}
operators.push(operator);
}
如果 token 不是运算符,那么它应该是一个数字。在这种情况下,首先检查运算符栈,如果栈不为空并且栈顶运算符的优先级高于当前 token 的运算符,就从栈中弹出运算符,并从数字栈中弹出两个数字进行计算,然后将结果推回数字栈中。然后,将当前 token 的运算符推到运算符栈中。
javaCopy code } else {
BigDecimal number = new BigDecimal(token);
if (isNegative) {
number = number.negate();
isNegative = false;
}
numbers.push(number);
}
如果 token 不是运算符,那么它应该是一个数字。在这种情况下,将 token 转换为 BigDecimal 数字,如果 isNegative 为真,就取其相反数,然后将结果推入数字栈中。
javaCopy code }
while (!operators.isEmpty()) {
BigDecimal b = numbers.pop();
BigDecimal a = numbers.pop();
char op = operators.pop();
BigDecimal result = performOperation(a, b, op);
numbers.push(result);
}
这个循环用于处理剩余的运算符和数字,直到运算符栈为空。对于每个运算符,从数字栈中弹出两个数字进行计算,然后将结果推回数字栈中。
javaCopy code
return numbers.pop();
最后,返回数字栈中的最终结果,这个结果就是整个表达式的计算结果。
这段代码的目的是解析一个包含数学表达式的字符串,并计算其结果,包括处理负数和运算符的优先级。