数据结构和算法-图的基本概念及邻接矩阵法和邻接表法和十字链表法和链表链表法

图的概念

总览

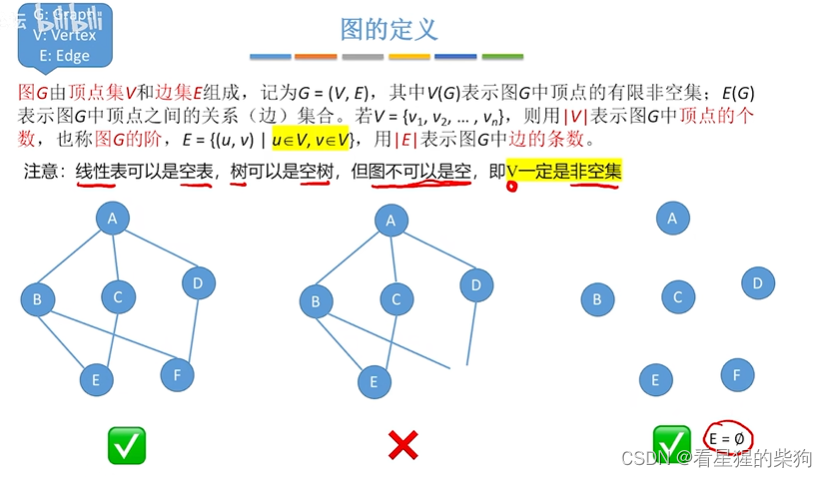
在这里插入图片描述

图的定义

顶点不能为空，边可以为空，且边对于两端必须要有顶点
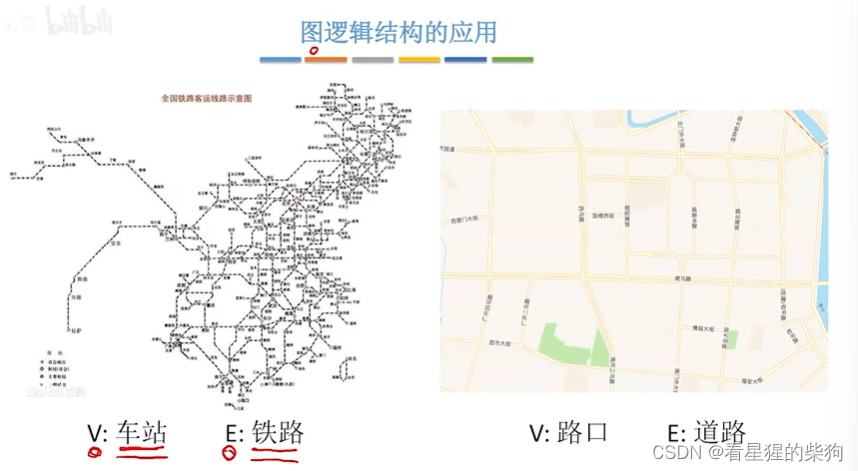
在这里插入图片描述

图逻辑结构的应用

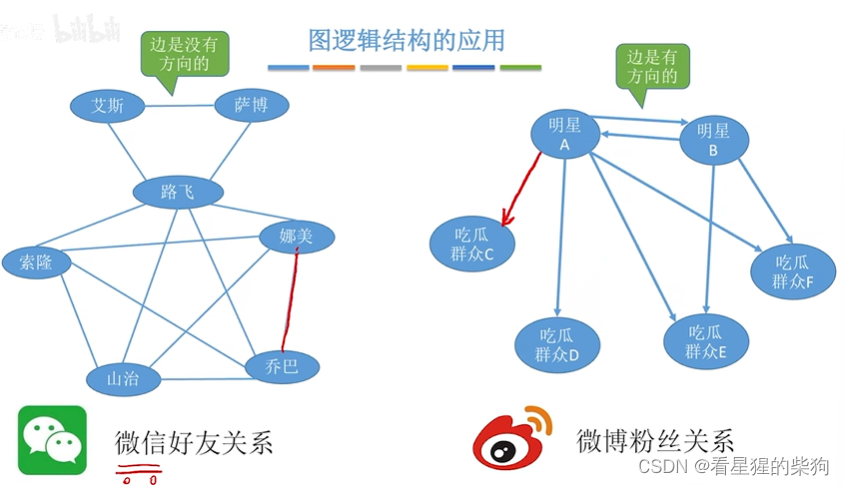
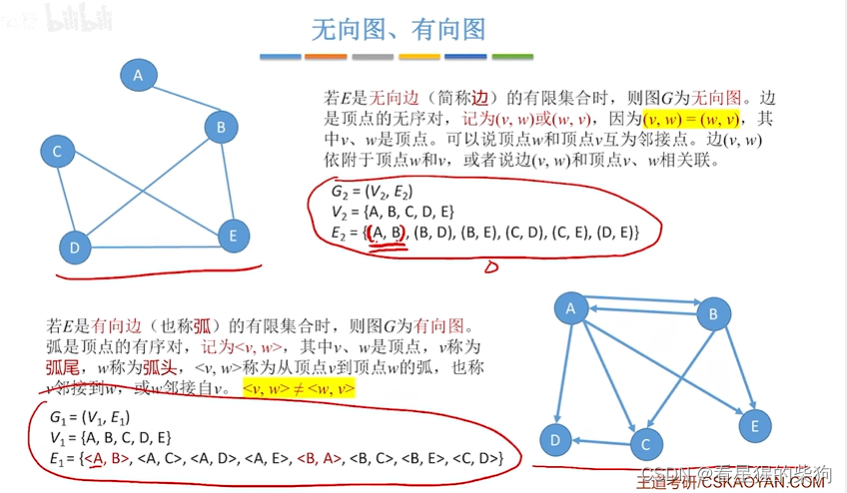
在这里插入图片描述

无向图和有向图

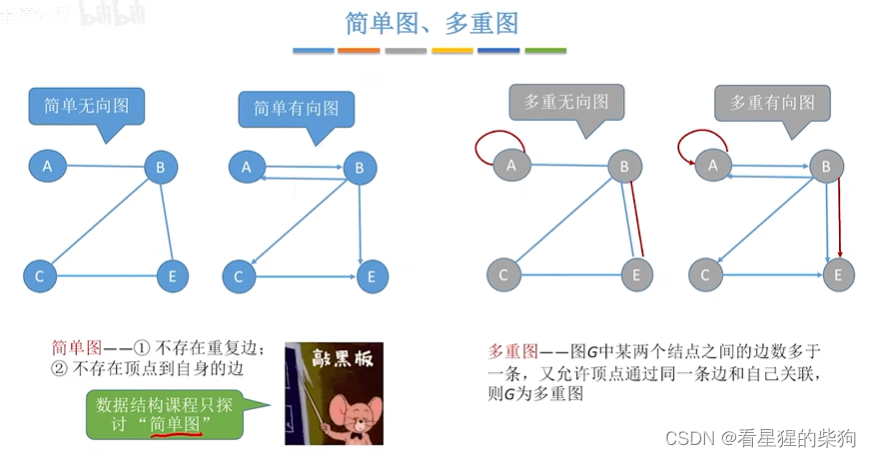
在这里插入图片描述

简单图和多重图

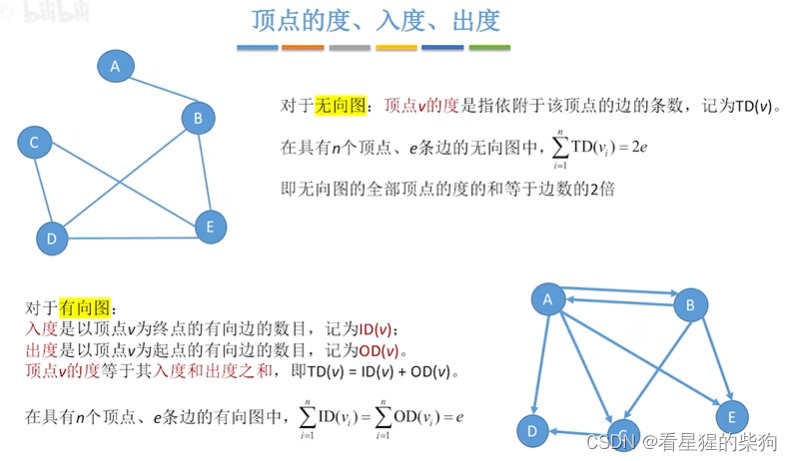
在这里插入图片描述

顶点的度，入读，出度

无向图中一条边对应两个节点产生两个度
有向图中一条边对应两个节点，一个节点产生入读，另一个节点产生出度
在这里插入图片描述

顶点-顶点的关系描述

连通（无向图中）：两个顶点有路径存在
强连通（有向图中）：两个顶点有来回路径
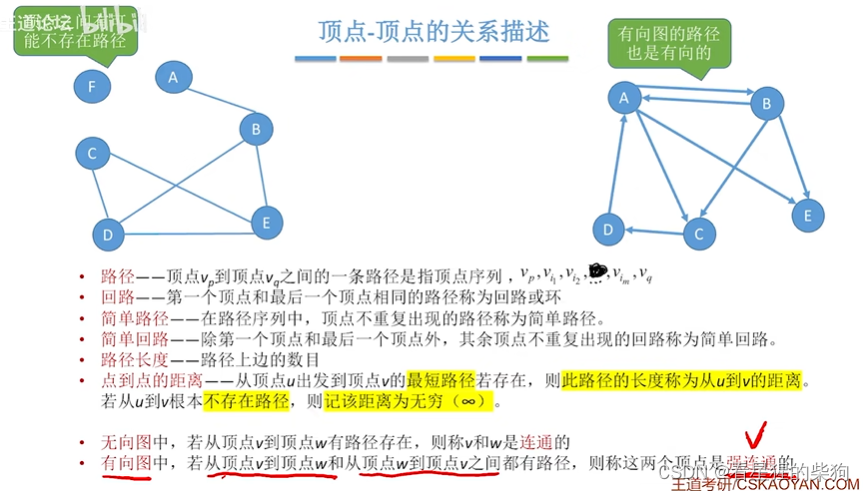
在这里插入图片描述

连通图，强连通图

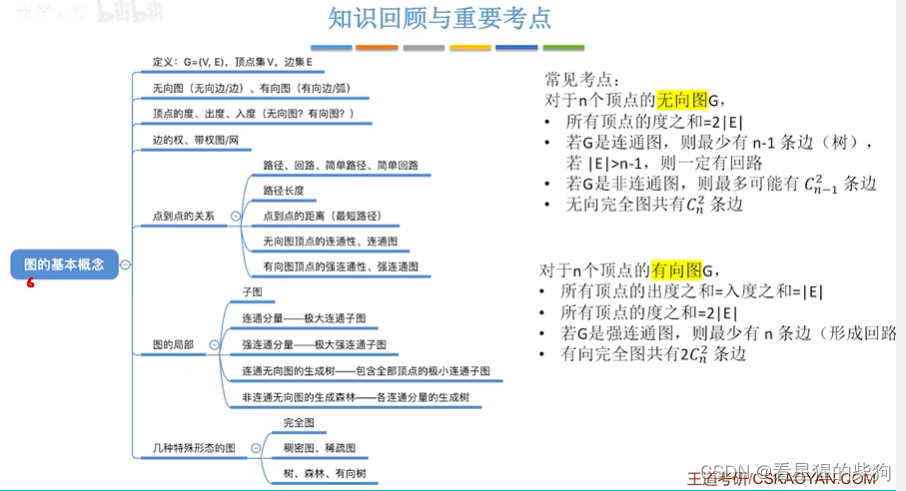
对于n个顶点的无向图G
若要为连通图，则保证n个顶点连成一条线即可，那么有n-1条边
若要为非连通图，则将一个顶点隔离，将剩余的节点的边连满，相当于是计算从n-1个顶点中选两个顶点的种类数有多少，此时连满后再增加任意条边，只能是隔离的那个顶点连接到剩余的节点上，此时将连通，所以不行。所以只需计算将剩余的节点的边连满的边数

对于n个顶点的有向图
若要为强连通图，则最少有n条边（即形成回路，此时任意一个顶点沿回路方向出发都能到达任何一个顶点）
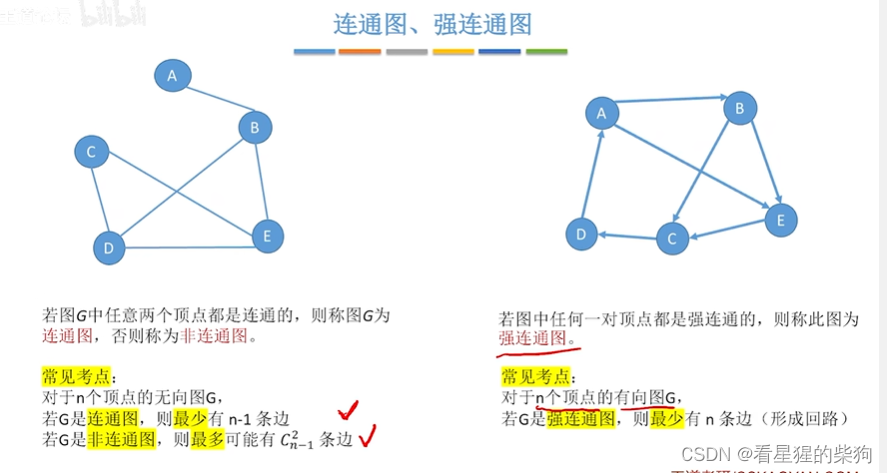
在这里插入图片描述

研究图的局部-子图

无向图和有向图对于子图相关的概念差不多
子图也是一个图，所以也要符合图的要求

无向图

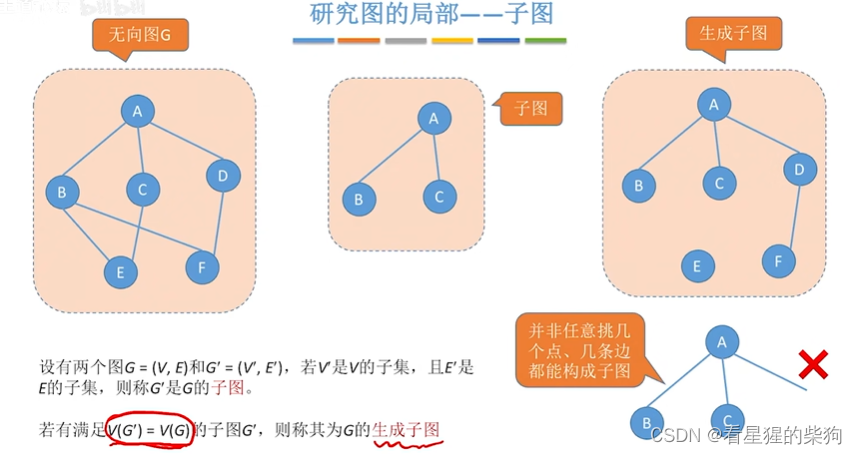
在这里插入图片描述

有向图

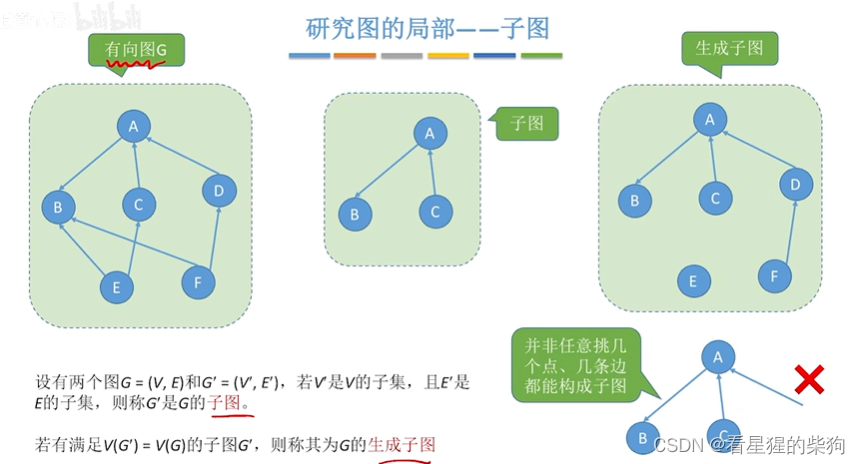
在这里插入图片描述

连通分量

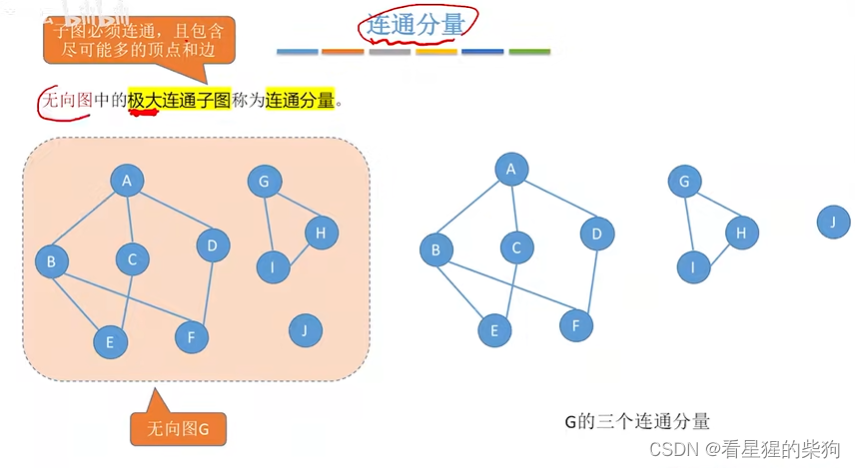
在这里插入图片描述

强连通分量

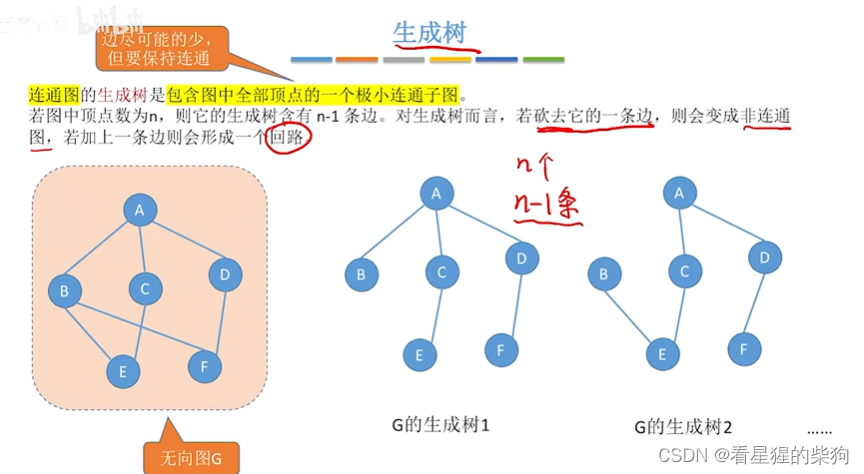
在这里插入图片描述

生成树

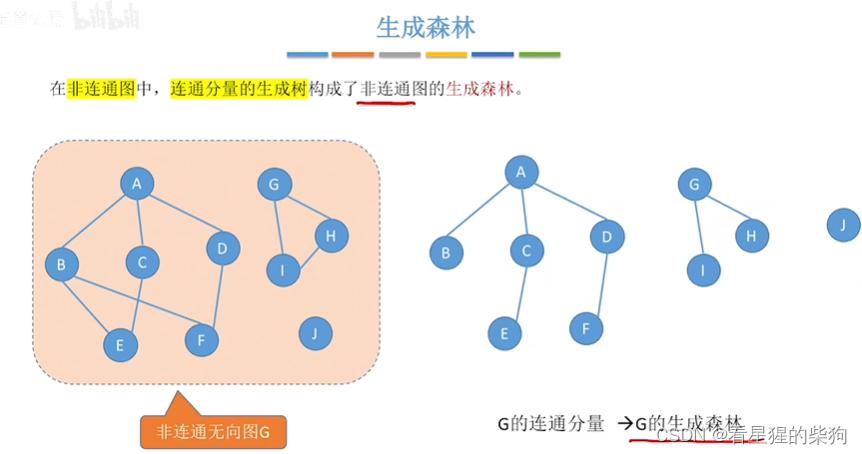
在这里插入图片描述

生成森林

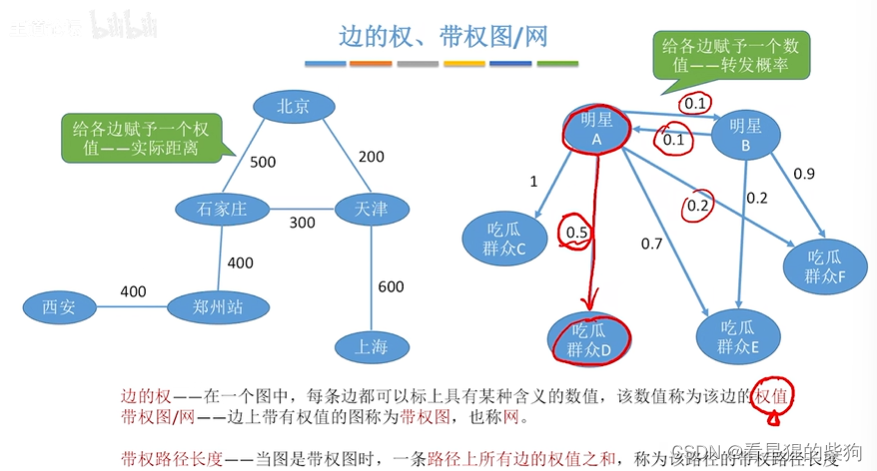
在这里插入图片描述

边的权，带权图/网

在这里插入图片描述

几种特殊形态的图

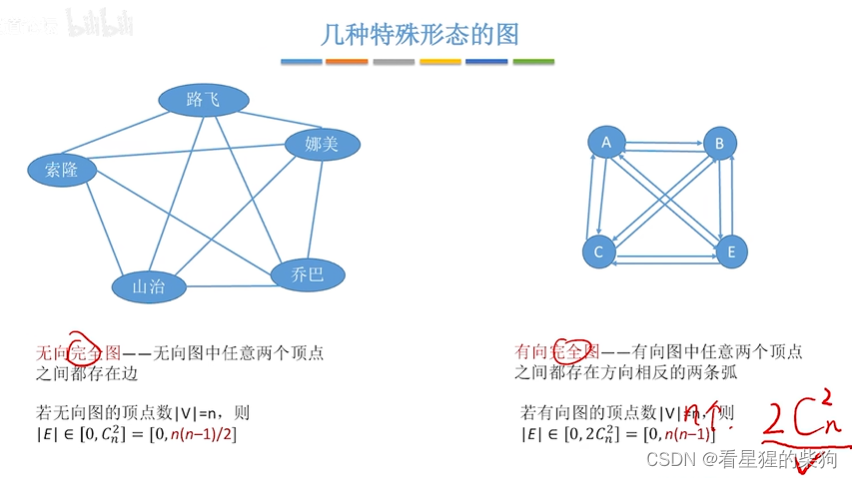
在这里插入图片描述

有向树不是强连通的

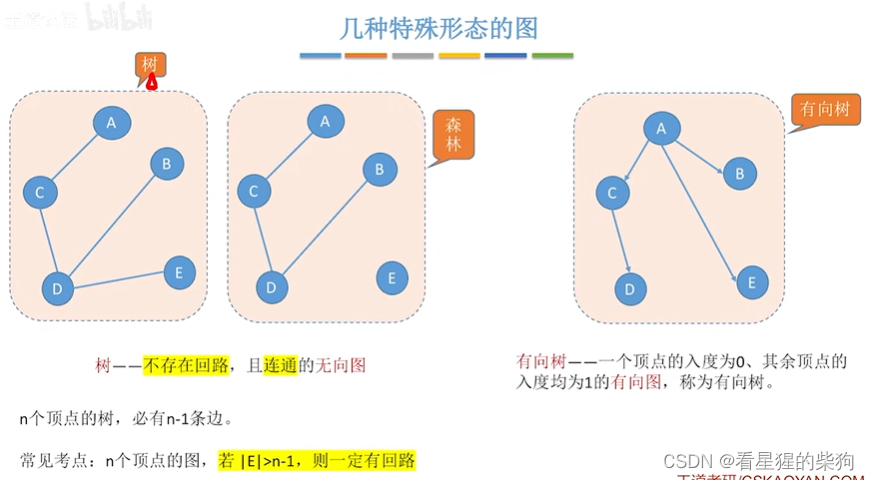
小结

在这里插入图片描述

邻接矩阵

总览

在这里插入图片描述

邻接矩阵

就是横坐标和纵坐标都为点的图，相连为1，不相连为0
领结的意思就是是否相邻连接
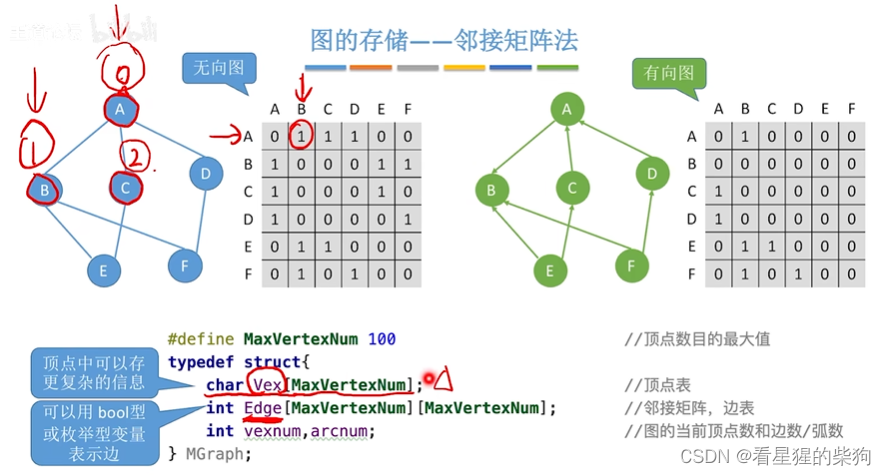
在这里插入图片描述

在这里插入图片描述

求顶点的度，入度，出度

无向图对应左边，有向图对应右边

在这里插入图片描述

邻接矩阵存储带权图

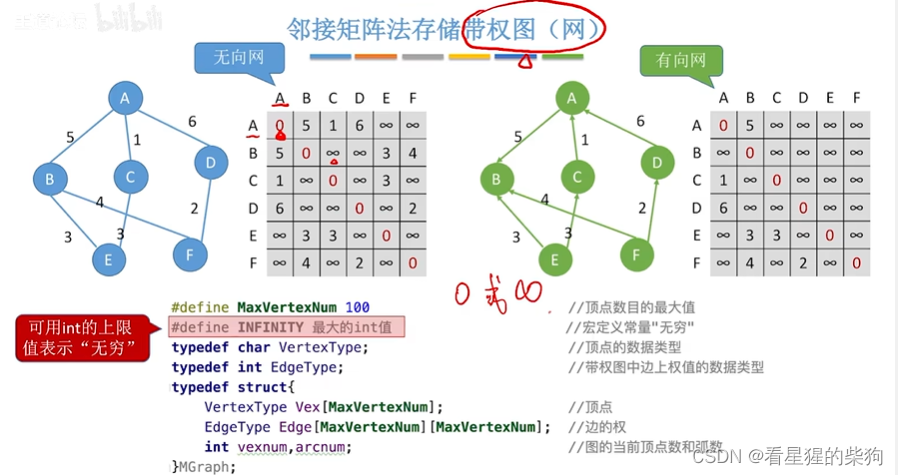
在这里插入图片描述

性能分析

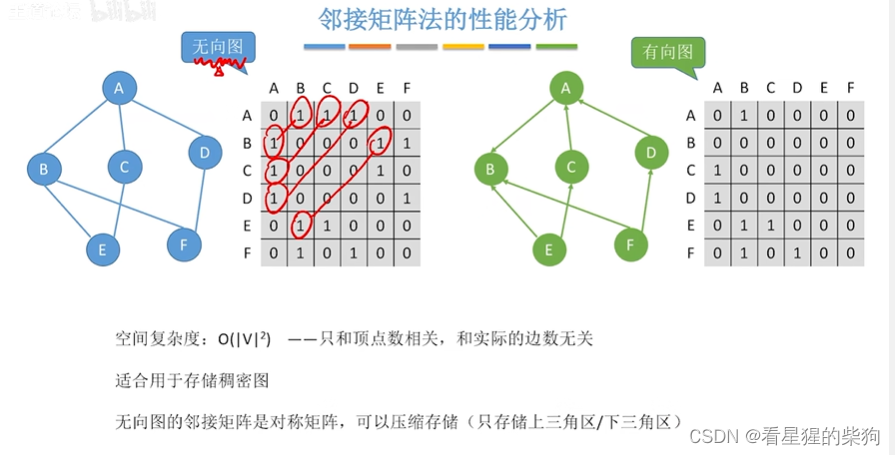
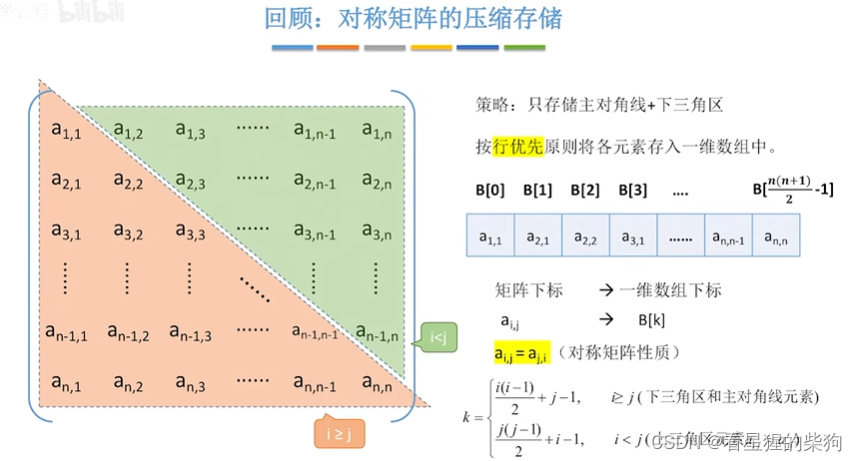
在这里插入图片描述

在这里插入图片描述

邻接矩阵法的性质

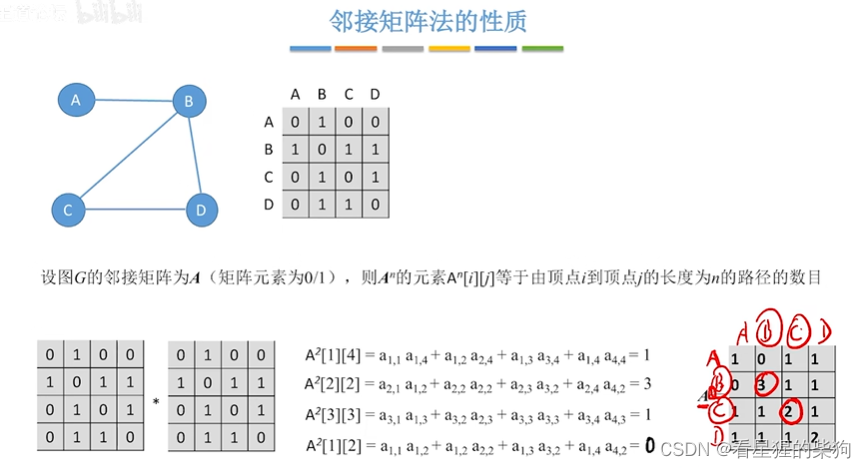
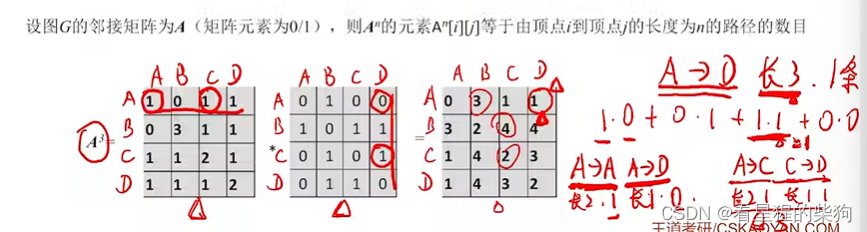
在这里插入图片描述

小结

在这里插入图片描述

邻接表

在这里插入图片描述

顺序+链式存储

用一维数组存图，每个顶点有对应边的指针相关信息
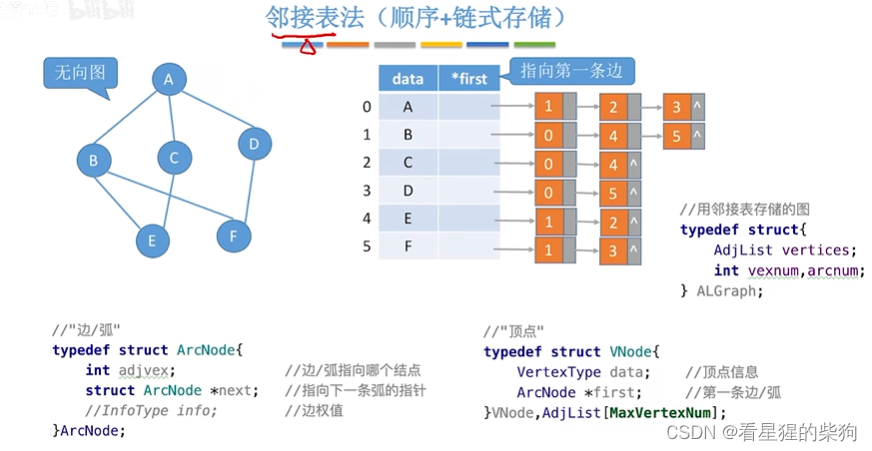
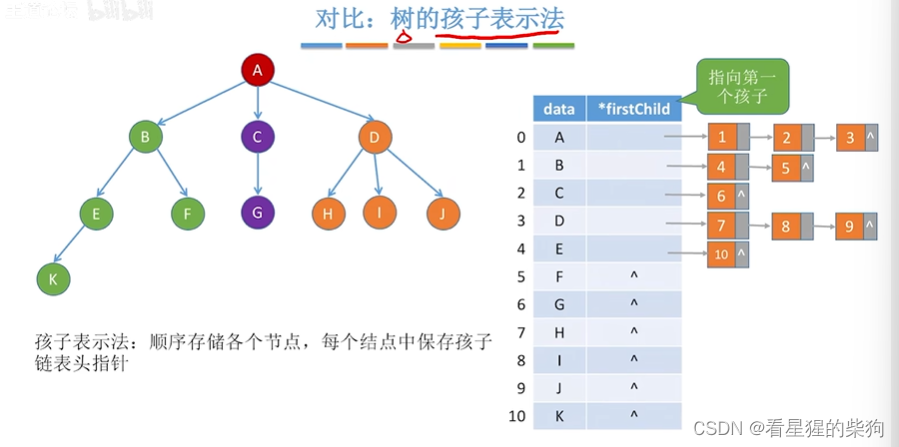
在这里插入图片描述

对比树的孩子表示法

在这里插入图片描述

有向图vs无向图

同一条边无向图需要存储两次，而有向图只需存储一次，所以空间复杂度有所不同
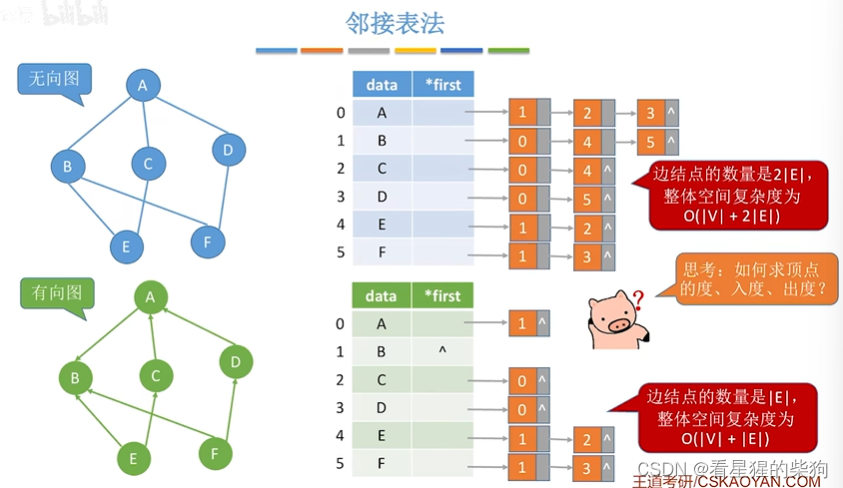
在这里插入图片描述

求顶点的度，入度，出度

无向图的度：只需遍历该节点对应的边链表
有向图的出度：只需遍历该节点对应的边链表
有向图的入度：需要遍历该节点之外的所有节点的边链表（麻烦）
有向图的度：即入度+出度

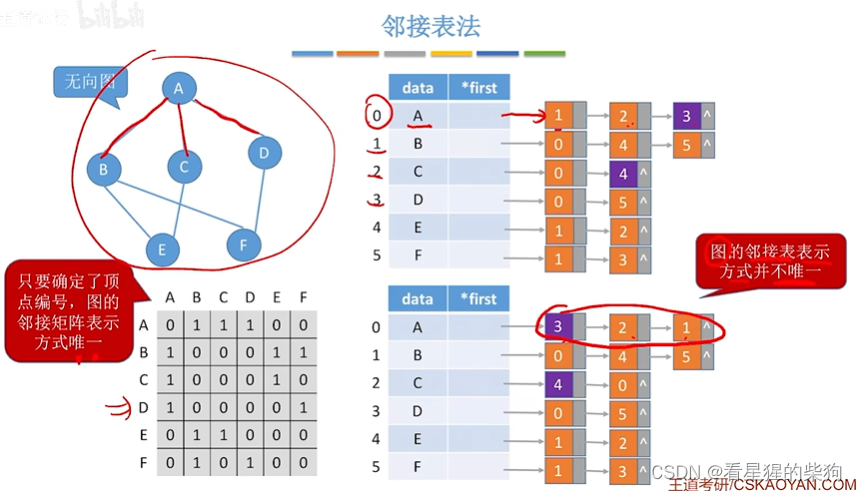
表示方式不唯一

即点的边链表不唯一
但图的邻接矩阵唯一
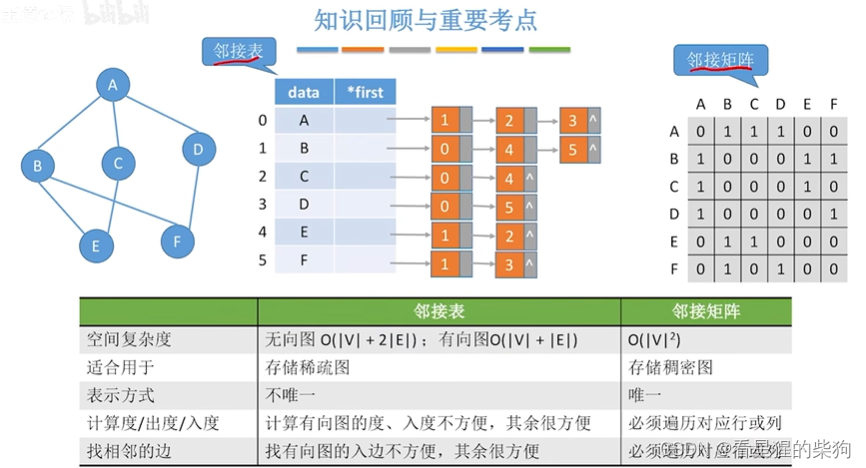
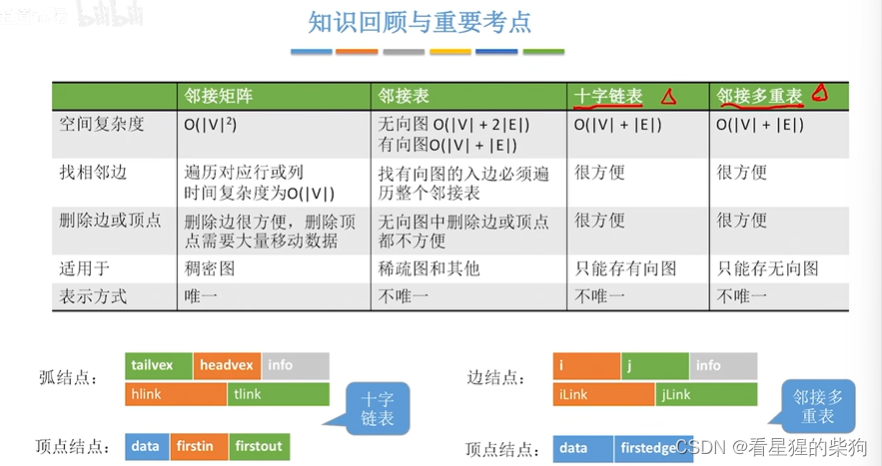
在这里插入图片描述

小结

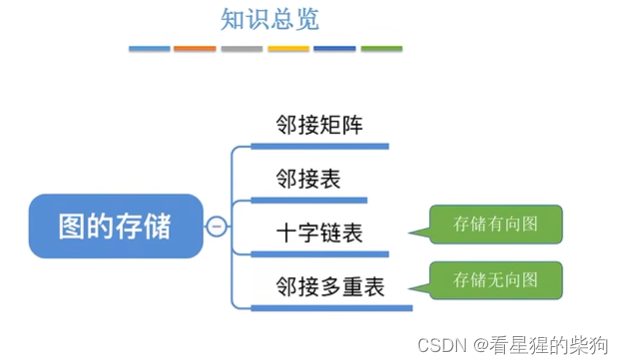
在这里插入图片描述

十字链表

总览

在这里插入图片描述

前提问题

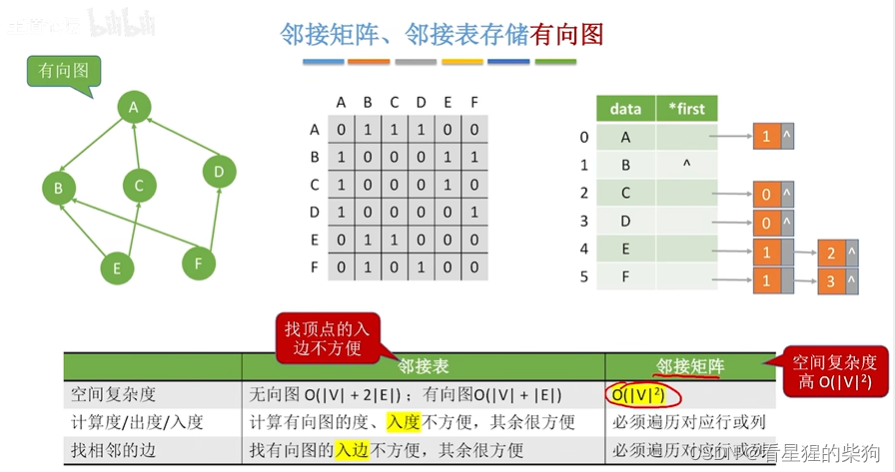
邻接矩阵存储空间复杂度高
而邻接表找入边不方便
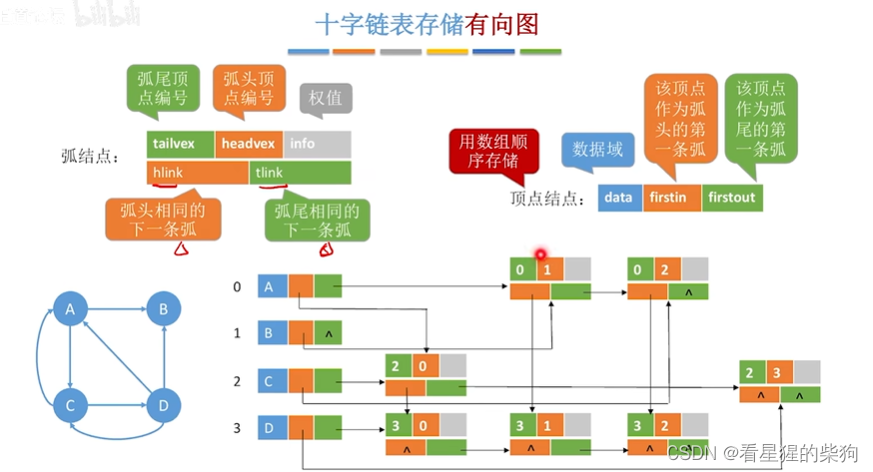
在这里插入图片描述

十字链表存储有向图

就是存储节点分别为弧的弧尾顶点和弧的弧头顶点的边链表
在这里插入图片描述

性能分析

在这里插入图片描述

邻接矩阵，邻接表存储无向图的缺点

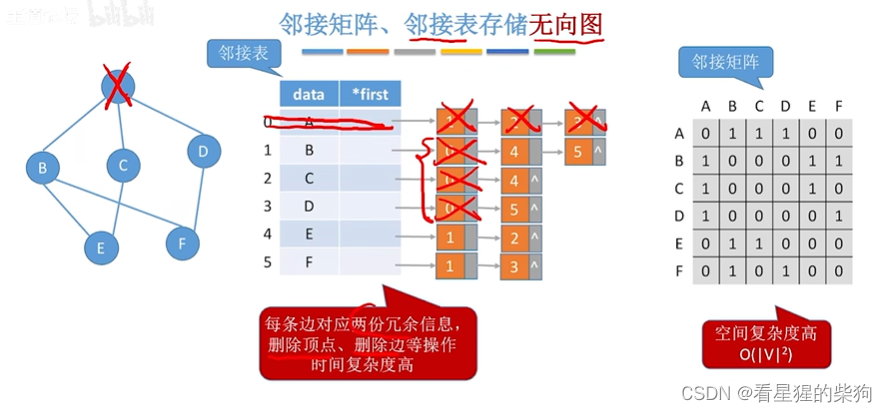
在这里插入图片描述

邻接多重表存储无向图

即一条边只有一个边元素对应，链表表示与某个顶点相连的边
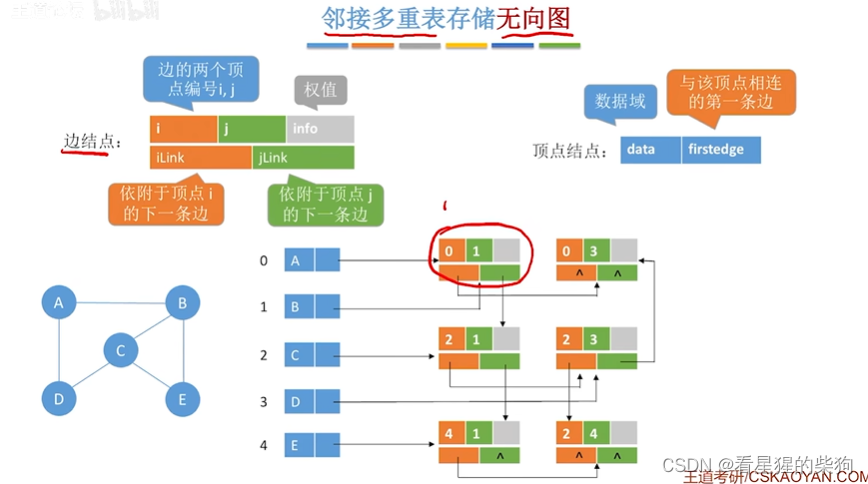
在这里插入图片描述
删除边时，只需要修改前一个的指针为后一个边的指针即可
删除点时,即将该点对应的边链表删除即可，同时修改指向该链表中元素的其他链表的元素指针

小结

在这里插入图片描述