代理模型：最小二乘支持向量回归(LSSVR)--- MATLAB程序

写在开头：

代理模型是工程问题中常用的一个优化方法。当实际问题计算量很大、不容易求解时，可以使用计算量较小、求解迅速的简化模型来替代原模型，加速优化过程。代理模型采用一个数据驱动的、自下而上的办法来建立：首先，通过抽样得到有限个样本点【输入，计算原模型的响应（输出）】；然后，基于抽样得到的样本点，建立代理模型替代高精度模拟模型。这一过程也被称为行为建模或者黑箱模型。如果只涉及唯一的变量，这一过程也被称为曲线拟合---转自：http://t.csdn.cn/kLWGh

目前代理模型通常有多项式响应面（RSM）模型、Kriging模型、径向基函数（RBF)、神经网络（NN)、支持向量回归（SVR)、多变量插值和回归（MIR）、多项式混沌展开（PCE)等等。在这里简单介绍一下最小二乘支持向量回归（LSSVR）。

LSSVR是一种优秀的基于统计学习理论的建模方法，具有训练速度快、泛化性能好和拟合非线性函数能力强等优点，其被广泛应用于建模、预测和模式识别等领域。

本文的理论部分引用了哈尔滨工业大学高润鹏博士的博士学位论文---《最小二乘支持向量回归机算法及应用研究》---第二章

一、最小二乘支持向量回归(LSSVR)

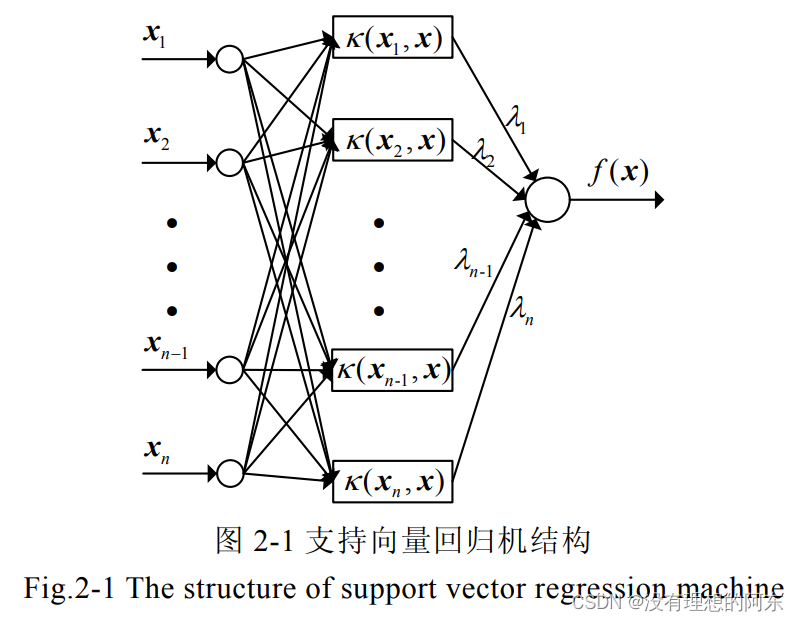
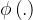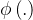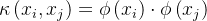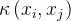支持向量机是 Vapnik 于 20 世纪 90 年代初提出的统计学习方法，其被广泛应用于建模预测、模式识别等领域。支持向量回归（Support vector regression SVR）是支持向量机的一个重要分支，用于解决建模问题。它通过非线性映射 $\small \phi \left ( . \right )$ 将输入空间映射到高维特征空间，在特征空间中求取最优线性函数，如图2-1所示。高维特征空间的维数可能是无穷维，并且通常不知道非线性映射 $\small \phi \left ( . \right )$ 的具体表达式，而采用核函数技术， $\small \kappa \left (x_{i},x_{j}\right )=\phi \left (x_{i}\right )\cdot \phi \left (x_{j}\right )$ ，（其中 $\small \kappa \left (x_{i},x_{j}\right )$ 是满足 Mercer 条件的核函数），通过非线性映射的内积代替非线性映射的直接计算，可明显简化计算。

LSSVR是 SVR的变形算法，Suykens 将不等式约束转变为等式约束，将损失函数由误差和转变为误差的平方和，求解算法由解凸二次优化问题转变为求解线性方程组问题，求解变量个数由 2n+1个减少到 n +1个，（n 为训练样本个数），因此 LSSVR 算法较 SVR算法求解难度降低，并且训练速度加快。

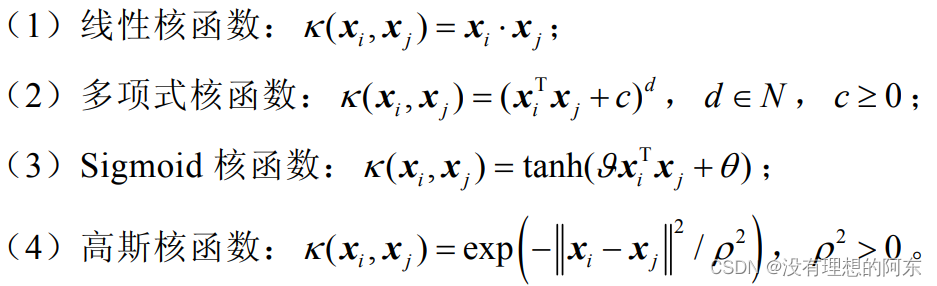
通过求解式(2-9)可得

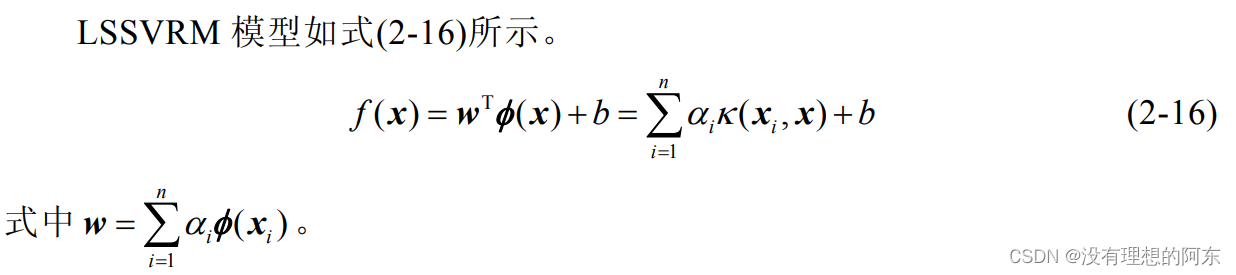
二、MATLAB实现

Case 1：

clear all
close all
clc

S=[0.700000000000000,59.6000000000000;2.10000000000000,82.7000000000000;4.70000000000000,75.1000000000000;4.80000000000000,52.8000000000000;5.90000000000000,67.1000000000000;6,35.7000000000000;6.40000000000000,33.7000000000000;7,46.7000000000000;8.20000000000000,40.1000000000000;13.3000000000000,0.600000000000000;13.3000000000000,68.2000000000000;13.4000000000000,31.3000000000000;17.8000000000000,6.90000000000000;20.1000000000000,66.3000000000000;22.7000000000000,87.6000000000000;23,93.9000000000000;24.3000000000000,73;24.8000000000000,15.1000000000000;24.8000000000000,26.3000000000000;26.4000000000000,58;26.9000000000000,65;27.7000000000000,83.3000000000000;27.9000000000000,90.8000000000000;29.1000000000000,47.9000000000000;29.5000000000000,89.4000000000000;30.1000000000000,6.10000000000000;30.8000000000000,12.1000000000000;32.7000000000000,40.2000000000000;34.8000000000000,8.10000000000000;35.3000000000000,32;37,70.3000000000000;38.2000000000000,77.9000000000000;38.9000000000000,23.3000000000000;39.4000000000000,82.5000000000000;43,4.70000000000000;43.7000000000000,7.60000000000000;46.4000000000000,84.1000000000000;46.7000000000000,10.6000000000000;49.9000000000000,22.1000000000000;51,88.8000000000000;52.8000000000000,68.9000000000000;52.9000000000000,32.7000000000000;55.5000000000000,92.9000000000000;56,1.60000000000000;60.6000000000000,75.2000000000000;62.1000000000000,26.6000000000000;63,12.7000000000000;69,75.6000000000000;70.5000000000000,83.7000000000000;70.9000000000000,11;71.5000000000000,29.5000000000000;78.1000000000000,45.5000000000000;78.2000000000000,9.10000000000000;78.4000000000000,20;80.5000000000000,55.9000000000000;81.1000000000000,51;83.8000000000000,7.90000000000000;84.5000000000000,11;85.2000000000000,67.3000000000000;85.5000000000000,73;86.7000000000000,70.4000000000000;87.2000000000000,55.7000000000000;88.1000000000000,0;88.4000000000000,12.1000000000000;88.4000000000000,99.6000000000000;88.8000000000000,82.9000000000000;88.9000000000000,6.20000000000000;90.6000000000000,7;90.7000000000000,49.6000000000000;91.5000000000000,55.4000000000000;92.9000000000000,46.8000000000000;93.4000000000000,70.9000000000000;94.8000000000000,71.5000000000000;96.2000000000000,84.3000000000000;98.2000000000000,58.2000000000000]
Y=[34.1000000000000;42.2000000000000;39.5000000000000;34.3000000000000;37;35.9000000000000;36.4000000000000;34.6000000000000;35.4000000000000;44.7000000000000;37.8000000000000;37.8000000000000;43.9000000000000;37.7000000000000;42.8000000000000;43.6000000000000;39.3000000000000;42.3000000000000;39.7000000000000;36.9000000000000;37.8000000000000;41.8000000000000;43.3000000000000;36.7000000000000;43;43.6000000000000;42.8000000000000;37.5000000000000;43.3000000000000;38.8000000000000;39.2000000000000;40.7000000000000;40.5000000000000;41.4000000000000;43.3000000000000;43.1000000000000;41.5000000000000;42.6000000000000;40.7000000000000;42;39.3000000000000;39.2000000000000;42.2000000000000;42.7000000000000;40.1000000000000;40.1000000000000;41.8000000000000;40.1000000000000;40.9000000000000;41.7000000000000;40.8000000000000;38.7000000000000;41.7000000000000;40.8000000000000;38.7000000000000;38.6000000000000;41.6000000000000;41.5000000000000;39.4000000000000;39.8000000000000;39.6000000000000;38.8000000000000;41.6000000000000;41.3000000000000;41.2000000000000;40.5000000000000;41.5000000000000;41.5000000000000;38.9000000000000;39;39.1000000000000;39.7000000000000;39.7000000000000;40.3000000000000;39.5000000000000]

S=max_min(S);
Y=max_min(Y);


figure(1)
plot3(S(:,1),S(:,2),Y,'.k', 'MarkerSize',10)%绘制原始散点数据

St=S;
Kenel_Matrix=Kenel(St,St);
n=size(St,1);
C=100;

%最小二乘支持向量回归
b_alpha=inv([[0,ones(1,n)];[ones(n,1),Kenel_Matrix+eye(n)/C]])*[0;Y];
b=b_alpha(1);
a=b_alpha(2:end);
%% %预测
X = gridsamp([0 0;1 1], 40);  
[m,~]=size(X);
YX=zeros(m,1);
for i=1:size(X,1)
    x=X(i,:);
    y=sum(a.*Kenel(St,x))+b;
    YX(i)=y;
end
X1 = reshape(X(:,1),40,40); X2 = reshape(X(:,2),40,40);
YX = reshape(YX, size(X1));
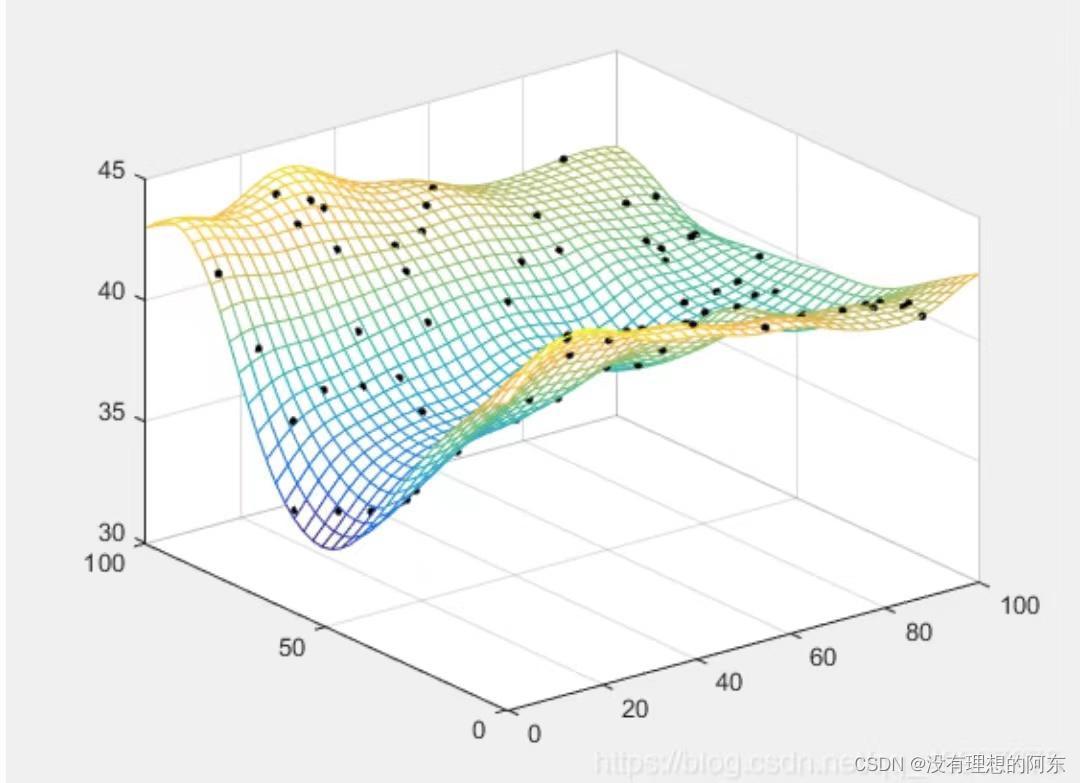
figure(2), mesh(X1, X2, YX)%绘制预测表面
hold on
plot3(S(:,1),S(:,2),Y,'.k', 'MarkerSize',10)%绘制原始散点数据

function [S] = Kenel(S1,X)

% GUASSIAN_KENEL 高斯核函数
dist=pdist2(S1,X);
delta=0.1;
S=exp(-dist.^2/(2*delta*delta));

% 拉普拉斯函数
% dist=pdist2(S1,X);
% delta=0.5;
% S=exp(-dist/delta);

end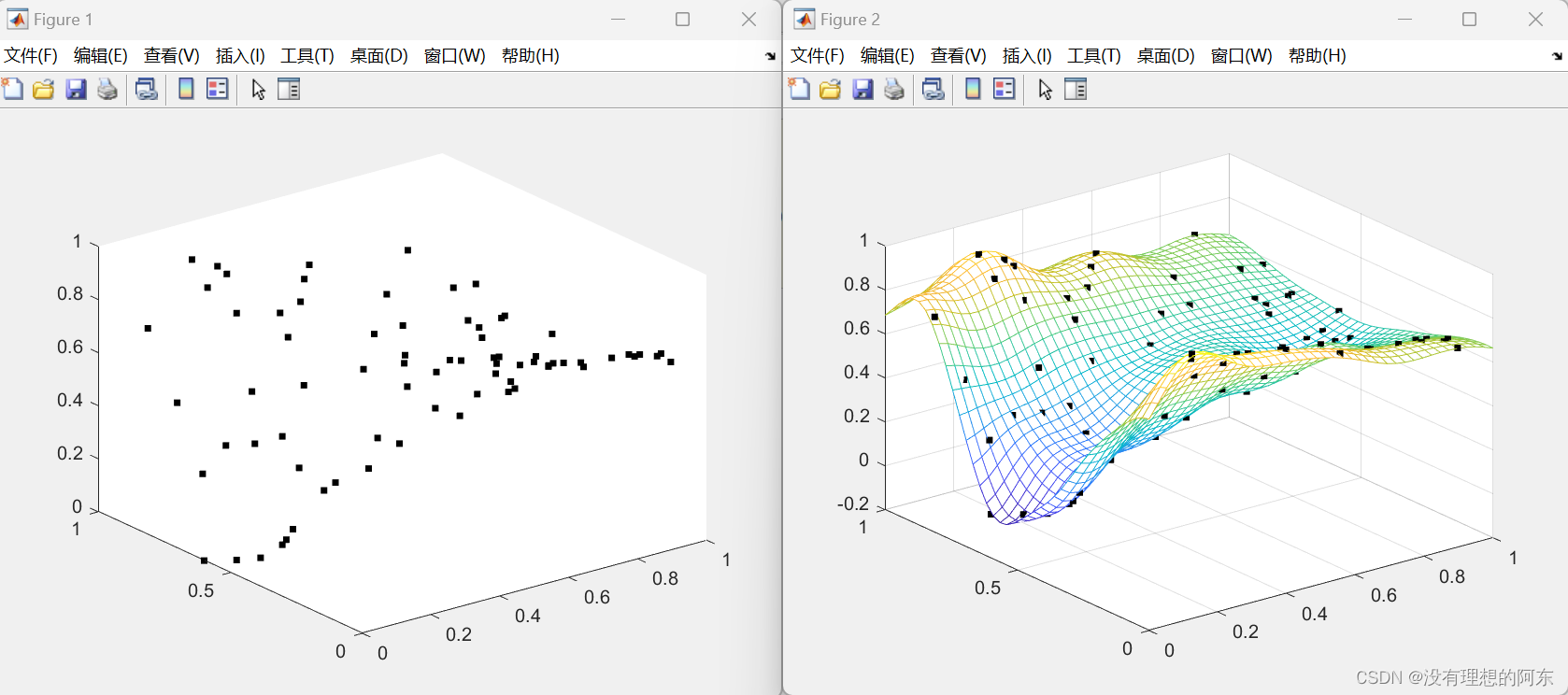

与克里金插值工具箱的结果基本一致，克里金插值详见 http://t.csdn.cn/n2kYT

Case 2：

clear all
close all
clc

S=[0:0.1:20]';%生成200个样本
temp=randperm(size(S,1),180)';
St=S(temp);%随机取180个样本作为训练样本，其余的样本作为测试样本
Y=sin(St);


Kenel_Matrix=Kenel(St,St);
n=size(St,1);
C=100;

%最小二乘支持向量回归
b_alpha=inv([[0,ones(1,n)];[ones(n,1),Kenel_Matrix+eye(n)/C]])*[0;Y];
b=b_alpha(1);
a=b_alpha(2:end);
X=S(setdiff([1:size(S,1)]',temp),:);
for i=1:size(X,1)
    x=X(i,:);
    y=sum(a.*Kenel(St,x))+b;
    YX(i,:)=[y,sin(x)];
end
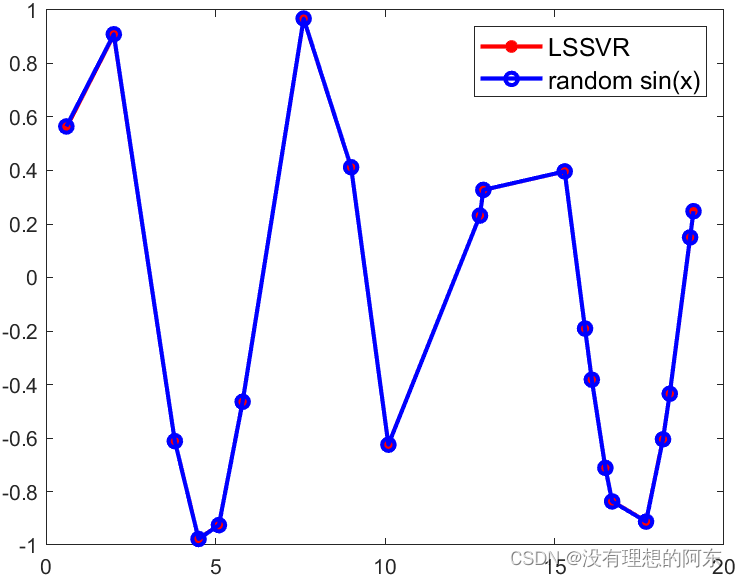
figure(2)
plot(X,YX(:,1),'-r*','LineWidth',2)
hold on
plot(X,YX(:,2),'-bo','LineWidth',2)
gca = legend('LSSVR','random sin(x)');
set(gca,'FontSize',12);

function [S] = Kenel(S1,X)

% GUASSIAN_KENEL 高斯核函数
dist=pdist2(S1,X);
delta=1;
S=exp(-dist.^2/(2*delta*delta));


end

其它子程序：

function [x] = max_min(x)
%数据归一化
for i=1:size(x,2)
    x(:,i)=(x(:,i)-min(x(:,i)))/(max(x(:,i))-min(x(:,i)));
end
end

function  S = gridsamp(range, q)
%GRIDSAMP  n-dimensional grid over given range
%
% Call:    S = gridsamp(range, q)
%
% range :  2*n matrix with lower and upper limits
% q     :  n-vector, q(j) is the number of points
%          in the j'th direction.
%          If q is a scalar, then all q(j) = q
% S     :  m*n array with points, m = prod(q)

% hbn@imm.dtu.dk  
% Last update June 25, 2002

[mr n] = size(range);    dr = diff(range);
if  mr ~= 2 | any(dr < 0)
  error('range must be an array with two rows and range(1,:) <= range(2,:)')
end 
sq = size(q);
if  min(sq) > 1 | any(q <= 0)
  error('q must be a vector with non-negative elements')
end
p = length(q);   
if  p == 1,  q = repmat(q,1,n); 
elseif  p ~= n
  error(sprintf('length of q must be either 1 or %d',n))
end 

% Check for degenerate intervals
i = find(dr == 0);
if  ~isempty(i),  q(i) = 0*q(i); end

% Recursive computation
if  n > 1
  A = gridsamp(range(:,2:end), q(2:end));  % Recursive call
  [m p] = size(A);   q = q(1);
  S = [zeros(m*q,1) repmat(A,q,1)];
  y = linspace(range(1,1),range(2,1), q);
  k = 1:m;
  for  i = 1 : q
    S(k,1) = repmat(y(i),m,1);  k = k + m;
  end
else    
  S = linspace(range(1,1),range(2,1), q).';
end