使用MATLAB进行傅里叶变换
1、定义
T=1;% 周期0-1
N=20;% 最大谐波
k=-N:N;% -20:20——-20表示a_(20)e^(j*20*w0*t)
N1=length(k);%N1=41
% ceil(N1/2)=21%即21是N1的中位数
t=linspace(0,T,100);
Nt=length(t);
tt=linspace(-4*T,4*T,1024);
Ntt=length(tt);
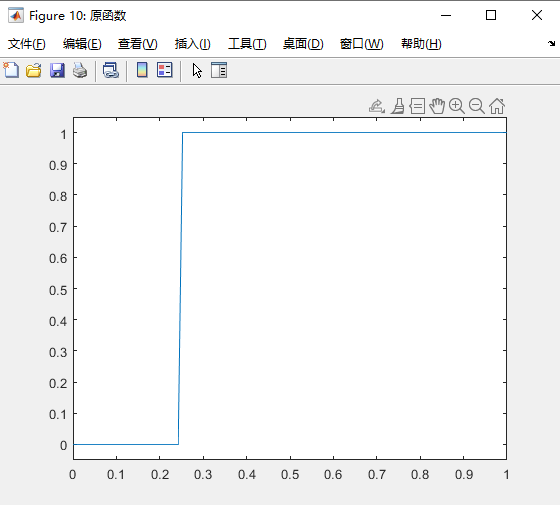
2、原函数
w0=2*pi/T;
% 0-T
xt=(t>=T/4).* 1.0;
fig10=figure(10);
fig10.Name='原函数';
plot(t,xt);
axis([t(1) t(Nt) min(xt)-0.05 max(xt)+0.05 ]);
3、原函数的周期延拓
N2=length(tt);
xx=zeros(1,N2);%size(a)=1*41,用于记录傅里叶级数的系数
for n=1:N2
for numT=-4:3
if (T/4+numT*T)<tt(n) && tt(n)<(T+numT*T)
xx(n)=1;
break
end
end
end
fig20=figure(20);
fig20.Name='原函数的周期延拓';
plot(tt,xx);
axis([tt(1) tt(Ntt) min(xx)-0.05 max(xx)+0.05 ]);
grid on 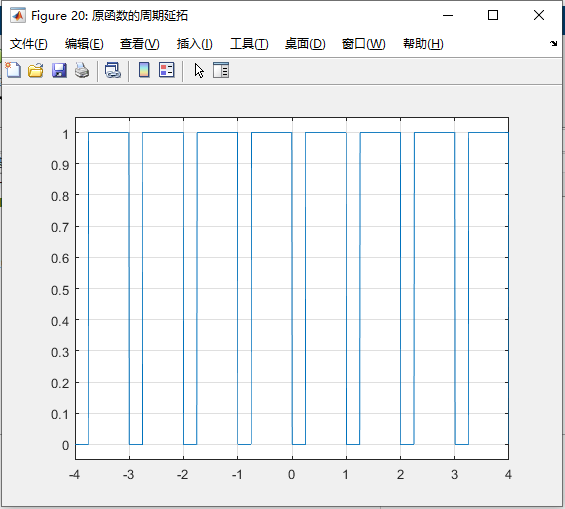
4、使用integral进行傅里叶变换
a=zeros(1,N1);%size(a)=1*41,用于记录傅里叶级数的系数
for n=1:N1
% a(n)=integral(@(x) signal0(x,k(n),T),0,T); %1
a(n)=integral(@(x) signal0(x,k(n),T),0,T,'RelTol',0,'AbsTol',1e-12);
% %解决《警告: 最小步长已快达到 x = 0.25。可能具有奇异性,或者容差可能对于此问题太小。 》
% RelTol - 相对误差容限
% AbsTol - 绝对误差容限
end
A=abs(a); %计算傅里叶变换的幅值
fig30=figure(30);
fig30.Name='傅里叶分解图';
subplot(3,1,1);stem(k,A);ylabel("a(k)幅值");
axis([k(1) k(N1) min(A)-0.05 max(A)+0.05]);% axis([ x起点 x终点 y起点 y终点]);
subplot(3,1,2); stem(k,real(a));ylabel('a(k)实部'); % real(F)
axis([k(1) k(N1) min(real(a))-0.05 max(real(a))+0.05 ]);
subplot(3,1,3);stem(k,imag(a));ylabel('a(k)虚部'); % imag(F)
xlabel('k');
axis([k(1) k(N1) min(imag(a))-0.05 max(imag(a))+0.05 ]);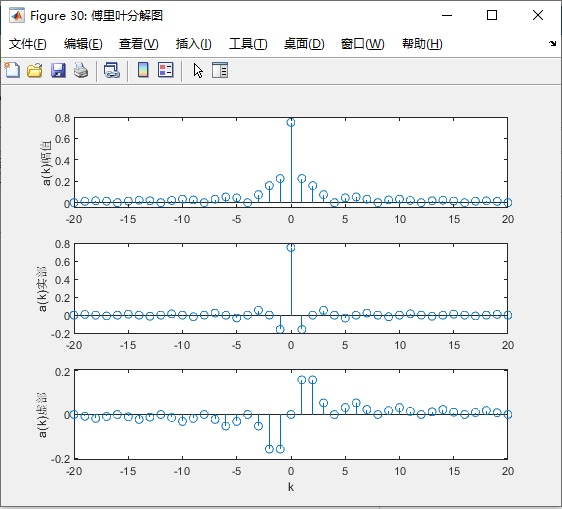
5、谐波分量
%基波分量
fundamental_component=a(ceil(N1/2))*exp(1i*0*w0*tt);
%一次谐波分量
% first_harmonic_component=a(ceil(N1/2)-1)*exp(-1i*1*w0*tt)+a(ceil(N1/2)+1)*exp(1i*1*w0*tt);
har=1;
first_harmonic_component=a(ceil(N1/2)-har)*exp(-1i*har*w0*tt)+a(ceil(N1/2)+har)*exp(1i*har*w0*tt);
%二次谐波分量
% second_harmonic_component=a(ceil(N/2)-2)*exp(-1i*2*w0*tt)+a(ceil(N/2)+2)*exp(1i*2*w0*tt);
har=2;
second_harmonic_component=a(ceil(N1/2)-har)*exp(-1i*har*w0*tt)+a(ceil(N1/2)+har)*exp(1i*har*w0*tt);
%三次谐波分量
har=3;
third_harmonic_component=a(ceil(N1/2)-har)*exp(-1i*har*w0*tt)+a(ceil(N1/2)+har)*exp(1i*har*w0*tt);
fig40=figure(40);
fig40.Name='傅里叶分解图';
subplot(3,1,1);
plot(tt,fundamental_component);
ylabel('基波分量');
subplot(3,1,2);
plot(tt,fundamental_component+first_harmonic_component+second_harmonic_component);
ylabel(sprintf('%d%s',2,'次谐波分量合成图'));
subplot(3,1,3);
plot(tt,fundamental_component+first_harmonic_component+second_harmonic_component+third_harmonic_component)
ylabel(sprintf('%d%s',3,'次谐波分量合成图'));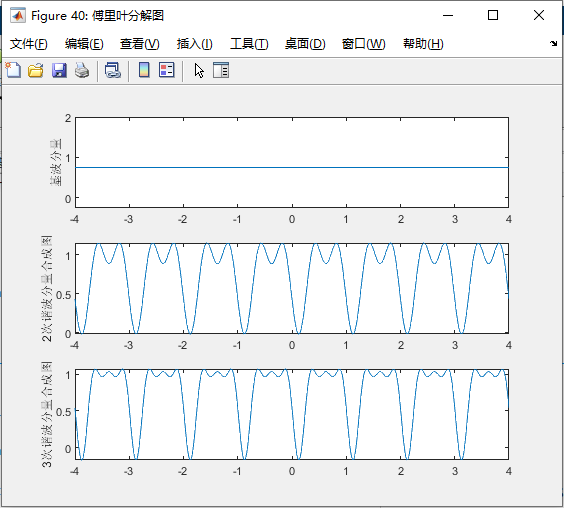
6、任意次谐波的傅里叶级数合成
xiebo=8;% 计算前xiebo次谐波分量的和
% tt=linspace(-4*T,4*T,1024);
fx=a(ceil(N1/2))*exp(1i*0*w0*tt);
for n=1:xiebo
fx=fx+a(ceil(N1/2)-n)*exp(-1i*n*w0*tt)+a(ceil(N1/2)+n)*exp(1i*n*w0*tt);
% n=1——第20次谐波分量
% a(1)*exp(1i*(1-20-1)*w0*tt)=a(1)*exp(1i*(-20)*w0*tt)
% n=N1=41——第20次谐波分量
% a(41)*exp(1i*(41-20-1)*w0*tt)=a(41)*exp(1i*(20)*w0*tt)
end
fig41=figure(41);
fig41.Name=sprintf('%d%s',xiebo,'次谐波分量合成图');
% f3=figure('Name','傅里叶合成图','IntegerHandle','on','Number',100)
plot(tt,fx)
grid on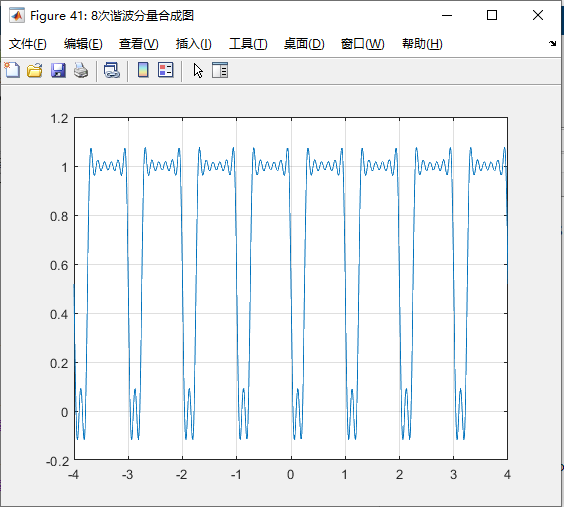
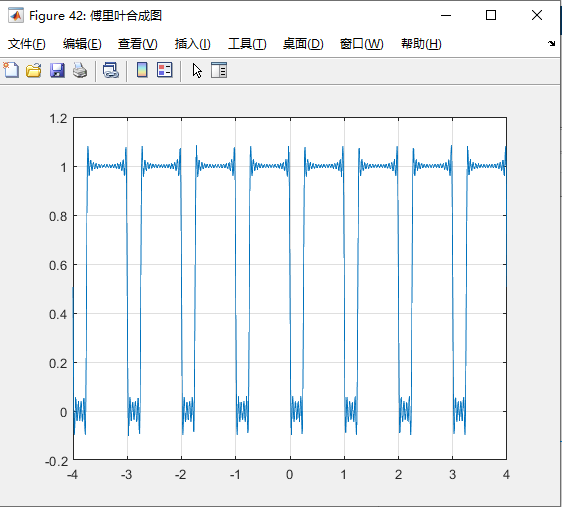
7、20次谐波的傅里叶级数合成
% tt=linspace(-4*T,4*T,1024);
fx=0;
for n=1:N1
fx=fx+a(n)*exp(1i*(n-N-1)*w0*tt);
% n=1——第20次谐波分量
% a(1)*exp(1i*(1-20-1)*w0*tt)=a(1)*exp(1i*(-20)*w0*tt)
% n=N1=41——第20次谐波分量
% a(41)*exp(1i*(41-20-1)*w0*tt)=a(41)*exp(1i*(20)*w0*tt)
end
fig42=figure(42);
fig42.Name='傅里叶合成图';
% f3=figure('Name','傅里叶合成图','IntegerHandle','on','Number',100)
plot(tt,fx)
grid on
8、局部函数——signal0
%程序signal0.m:定义求傅里叶级数的系数的被积函数: y=(1/T)*x(t).*exp(-j*(2*pi/T)*k*t)
function y=signal0(t,k,T) %T为信号周期,t为时间变量,k为k次谐波
x=(t>=T/4).* 1.0;
% 定义占空比为25%的非对称周期方波for one period=T
% 对称周期三角形可定义:x=(abs(t)<=T/4). * (1-abs(t))
% 占空比为50%的对称周期方波可定义:x=(abs(t)<=T/4). *1.0
y=(1/T).*x.*exp(-1i*k*(2*pi/T)*t);
end