一文速览扩散模型优化过程:从DDPM到条件生成模型Stable Diffusion
文章目录
目前AIGC可以说是整个人工智能领域的当红炸子鸡,而Diffusion Model(扩散模型)正是目前各项图像生成式应用的主要架构。本人并不主要研究图像生成领域,不过由于项目需要也对其进行过一些调研,故写下这篇文章进行分享与记录。本文会从最简单的扩散模型开始讲起,然后根据原始模型存在的缺点介绍当前的一些改进方法,最后介绍一个经典的可用于条件生成的扩散模型Stable Diffusion。
1、扩散模型简介 - Diffusion Model
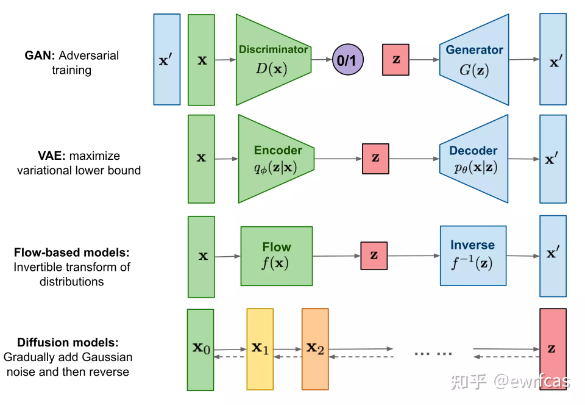
如下图所示,目前的图像生成式模型主要可以分为四类:① 首先是生成对抗网络GAN通过一种生成对抗式的方式进行学习,其生成器 G G G根据潜在空间的采样 z z z生成图像 x ′ x' x′,判别器 D D D则判断输入图像是真实图像 x x x还是生成图像 x ′ x' x′;② 变分自编码器VAE通过编码器学习图像分布 p ( x ) p(x) p(x)到先验分布 p ( z ) p(z) p(z)之间的转换,解码器学习 p ( z ) p(z) p(z)到 p ( x ) p(x) p(x)的转换关系,其在数学上可以被视为通过最大化ELBO进行优化;③ 标准化流模型则是通过构造一个可逆的变换,建立图像分布 p ( x ) p(x) p(x)与某个已知分布 p ( z ) p(z) p(z)的变换;④ 最后是扩散模型Diffusion Model,其通过逐步增加高斯噪声将其变为纯高斯噪声 z z z,再通过对 z z z逐步去噪生成新的图像。
简单地说,扩散模型就分为两个过程:“加噪”和“去噪”(也称为前向过程和逆向过程)。
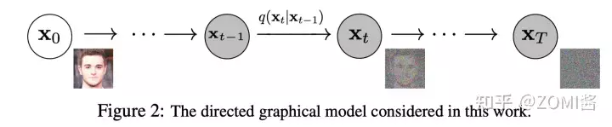
- 加噪过程:不断地往输入数据中加入噪声,直到其就变成纯高斯噪声,每个时刻都要给图像叠加一部分高斯噪声。其中后一时刻是前一时刻增加噪声得到的。
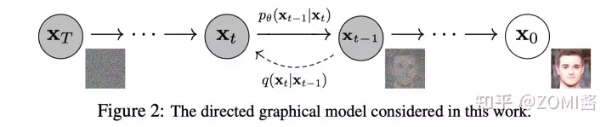
- 去噪过程:由一个纯高斯噪声出发,逐步地去除噪声,得到一个满足训练数据分布的图片。
在数学上可以将扩散模型的前向和逆向过程理解为马尔科夫链,其特点是"无记忆性",即下一状态的概率分布只能由当前状态决定,与之前的事件均与之无关。
在下一节本文将详细介绍具体的加噪过程与去噪过程,以及整体的学习流程。
2、最简单的扩散模型 - DDPM
我们从Denoising Diffusion Probabilistic Models(DDPM)这个工作出发来分析扩散模型的前向与逆向过程
前向加噪过程
首先对于前向加噪过程涉及两个公式:
- α t = 1 − β t \alpha_t = 1 - \beta_t αt=1−βt,其中 β \beta β会随着时间步长 t t t线性增大(0.0001->0.02),从而 α \alpha α越来越小;
- x t = α t x t − 1 + 1 − α t z t x_t= \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z_t xt=αtxt−1+1−αtzt ,其中 x t − 1 x_{t-1} xt−1是前一阶段的图像,z是一个满足标准高斯分布的噪音。
可以看到,模型的加噪其实就是将上一阶段输入的图像与一个高斯分布采样进行加权融合,权重随着时间步长而繁盛变化,可以看到一开始所加噪声幅度比较少,越往后噪声幅度逐渐增加。并且根据上面两个式子,我们可以推算得到任意时刻下
x
t
x_t
xt与
x
0
x_0
x0的关系(根据
t
t
t和
x
0
x0
x0直接得到
x
t
x_t
xt):

其中的 a t ^ \hat{a_t} at^是 t t t个时间内的 a t a_t at的连乘项
根据上式可以得到,当时间步长 t t t足够大时,最终输出 x t x_t xt就会变成一个标准高斯分布(因为α小于1,并且其随着时间一直衰减)。
逆向去噪过程
去噪过程仍然是逐步进行的,其需要根据
x
t
x_t
xt得到
x
t
−
1
x_{t-1}
xt−1,我们利用贝叶斯公式进行推导。如果我们已知
x
t
x_t
xt和
x
0
x_0
x0去求
x
t
x_t
xt,其贝叶斯公式如下所示:
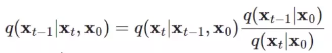
其中等式右边都可以通过前向加噪过程中的推理公式求得每一项的分布,如下所示:
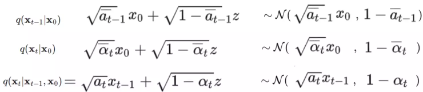
将这些正态分布代入到贝叶斯公式中(利用正态分布的乘除规则),得到下式:
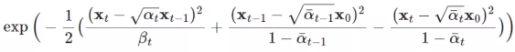
然后进行化简+合并同类项+配方, 如下所示。其中
σ
\sigma
σ方差已知的 → 常数(绿色框)。然后可以进一步计算得到
μ
\mu
μ的表达式。

需要注意这个过程要对X0进行换算,使得最后的结果只与Xt相关(此外还有一个待求参数 z t z_t zt)
经过上式的推导我们就能得到分布 p ( x t − 1 ∣ x t ) p(x_{t-1}|x_t) p(xt−1∣xt),其满足某个高斯分布。在这个分布中,方差是已知的(由α和β组成),而均值与 x t x_t xt还有一个高斯噪声 z t z_t zt相关,其中 x t x_t xt是已知的。因此,我们只要求得这个 z t z_t zt,就可以得到从 x t x_t xt得到 x t − 1 x_{t-1} xt−1的分布(知道了高斯分布的均值和方差)。而Diffusion Model采用一个深度模型 m o d e l ( X t , t ) model(X_t,t) model(Xt,t)去预测轮次 t t t的噪声 z t z_t zt,根据 x t x_t xt和 z t z_t zt,我们就可以得到去噪后的 x t − 1 x_{t-1} xt−1。这个模型采用U-Net结构(共享权重-所有时间轮次都只用这一个模型)。
训练与推理流程

左边是训练过程:随机选择一张图片,均匀采样得到时间轮次t,并从标准正态分布采样得到噪声ε【这也会当做U-Net训练时的label】,通过公式得到第
t
t
t轮加噪后的图像。将噪声图像和时间步长一起输入网络预测噪声值
z
t
z_t
zt,计算其与采样噪声ε之间的loss来更新模型参数(即U-Net网络);
训练主要关注的是逆向去噪过程,训练的目标也是让U-Net能够根据 x t x_t xt和 t t t得到噪声 z t z_t zt.
右边是生成过程:先从标准高斯分布中随机采样得到 X T X_T XT,然后利用噪声预测模型预测每一轮次的噪声 z t z_t zt,并根据上面推导的从 x t x_t xt到 x t − 1 x_{t-1} xt−1的公式进行逐步去噪。
模型优缺点
对于一个图像生成模型,存在三个方面的考虑:1. 高质量样本;2. 生成多样性;3. 高效快速的采样。但这三者之间往往难以权衡:
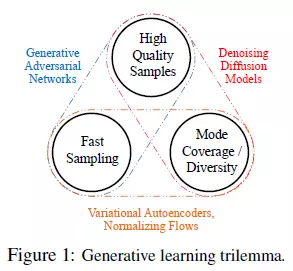
- GAN可以生成高质量的结果,同时可以快速采样,但是生成结果缺乏多样性,而且GAN网络训练过程中会出现不稳定和模式坍塌的问题;
- VAE和Normalizing Flows可以快速采样,而且生成的结果也有良好的多样性, 但是生成的质量却比较差;
- Diffusion生成的结果质量比较高,甚至可以超过GAN, 而且结果也有良好的多样性,但是Diffusion需要几百甚至几千步的采样,这导致训练与推理十分缓慢。此外,Diffusion Model的训练也比较容易(相比于GAN)。
在下一节中,本文将会介绍一个用于减少Diffusion Model采用次数的工作。
3、减少扩散模型的采样步骤 - DiffusionGAN
Tackling the Generative Learning Trilemma with Denoising Diffusion GANs
目前已有很多工作提出用于减少扩散模型的采样次数,这里介绍其中一项工作 - DiffusionGAN,其核心在于通过使用生成对抗模型来进行large step的快速采样。
不过目前主要流行的方法主要是DDIM()
首先回顾Diffusion Model,其有两个重要假设:1. 去噪过程的分布 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)是高斯分布;2. 去噪过程的步数需要数百/数千的数量级。这里也引申出两个问题:
- 去噪过程真实分布是高斯分布吗?或者在什么条件下是高斯分布?
- 去噪过程的步数多少与高斯分布的假设是否相关?
分析高斯分布、采样步长
我们先回顾上一节用到的贝叶斯公式: q ( x t − 1 ∣ x t ) ∝ q ( x t ∣ x t − 1 ) q ( x t − 1 ) q(x_{t-1}|x_t)\propto q(x_{t}|x_{t-1})q(x_{t-1}) q(xt−1∣xt)∝q(xt∣xt−1)q(xt−1),其中前向加噪过程的分布 q ( x t ∣ x t − 1 ) q(x_{t}|x_{t-1}) q(xt∣xt−1)服从高斯分布。那么在如下两种情况下,去噪过程满足高斯分布:
- 当步长 β t \beta_t βt无限小的时候,这时候贝叶斯项中的 q ( x t ∣ x t − 1 ) q(x_{t}|x_{t-1}) q(xt∣xt−1)占主导,无论 q ( x t ) q(x_{t}) q(xt)是什么形式,真实的去噪过程的分布与前向过程相同,都是高斯分布,这也是Diffusion Models需要大量采样步骤的原因;
因为 q ( x t ) q(x_{t}) q(xt)和 q ( x t − 1 ) q(x_{t-1}) q(xt−1)的分布基本一致
- 当数据边缘分布 q ( x t ) q(x_{t}) q(xt)是高斯分布时,那么真实的去噪分布也是高斯分布的形式,因此有一种做法就是通过VAE将其编码到高斯分布,再利用Diffusion模型(但这个VAE很难学)。
高斯分布相乘仍然还是高斯分布
所以当两个条件都不满足时,真实的去噪过程分布会变得很复杂:

上图是在一维数据集上模拟前向加噪过程的各数据分布,可以看到:采用较小的采样步长时,真实去噪过程分布满足高斯分布,如果步长过大,真实去噪分布将变得非常复杂(几种高斯混合在一起)。这说明在DDPM中,需要具有较多的采样step的必要性,但这也影响着模型在推理时的采样速率。
Diffusion GAN
DiffusionGAN的目标是当数据分布不为高斯分布时减少采样的步数。在这种情况下,真实去噪分布也不再服从高斯分布形式,那么建模的反向过程的分布
p
θ
(
x
t
−
1
∣
x
t
)
p_\theta(x_{t-1}|x_t)
pθ(xt−1∣xt)也不再是高斯分布。因此diffusionGAN直接采用Conditional GAN去直接学习去噪分布(即
q
(
x
t
∣
x
t
−
1
q(x_t|x_{t-1}
q(xt∣xt−1),而不是显式地去学习高斯分布的均值和方差。它训练目标是拟合真实的去噪过程分布,如下所示:
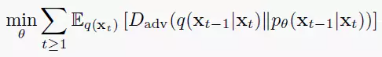
其中GAN的判别器优化目标是去区分真实去噪过程分布与模式输出的去噪分布:
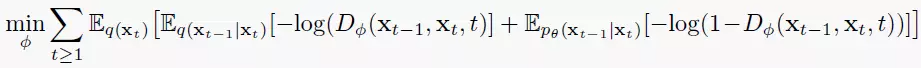
但是我们也无法知道真实的去噪过程分布
q
(
x
t
−
1
∣
x
t
)
q(x_{t-1}|x_{t})
q(xt−1∣xt)到底是什么,因此使用如下定义去重写第一项:
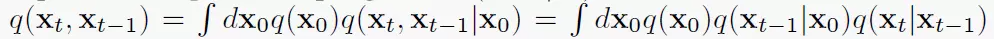
最终使得第一项变为下式:
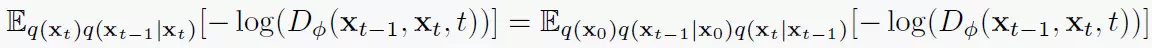
利用条件概率的特性,将真实去噪分布 q ( x t ) q ( x t − 1 ∣ x t ) q(x_{t})q(x_{t-1}|x_{t}) q(xt)q(xt−1∣xt)一起进行转换成 q ( x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x t − 1 ) q(x_{0})q(x_{t-1}|x_{0})q(x_t|x_{t-1}) q(x0)q(xt−1∣x0)q(xt∣xt−1),而这三项我们是比较公式直接可定义的
而GAN的生成器优化目标就是反着来,即让判别器无法分辨模型输出分布和真实分布:
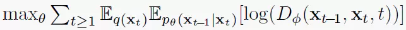
Diffusion GAN模型的整体架构如下所示:判别器需要输入
x
t
−
1
,
x
t
,
t
x_{t-1},x_t,t
xt−1,xt,t三项,判断输入的
x
t
−
1
x_{t-1}
xt−1是真实的还是模型模拟得到的。根据输入的
x
0
x_0
x0就可以在前向过程中直接得到真实的
x
t
−
1
x_{t-1}
xt−1和
x
t
x_t
xt,这样就解决了真实分布下的数据。而生成器则是根据输入的
x
t
x_t
xt直接得到完全去噪后的
x
0
′
x'_0
x0′,然后再对
x
0
′
x'_0
x0′进行一次posterior sampling去得到
x
t
−
1
′
x'_{t-1}
xt−1′,得到模型预测的结果:
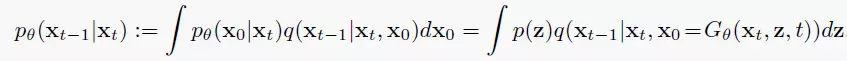
这个过程就类似于DDPM的采样过程,只不过我们直接得到了 x 0 x_0 x0和 x t x_t xt,直接算出 x t − 1 x_{t-1} xt−1就可以了(在DDPM预测噪声 z t z_t zt也是为了得到 x 0 x_0 x0)
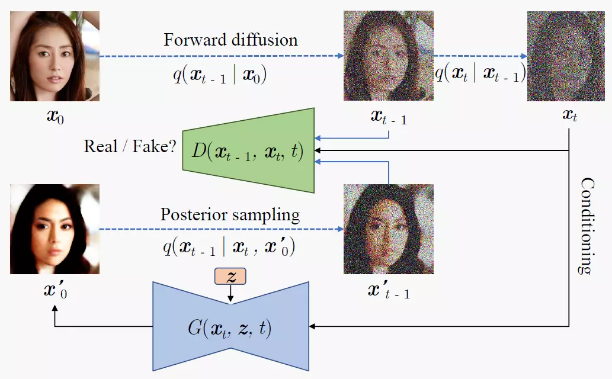
总结:生成器的目标是根据 x t x_t xt得到 x 0 ′ x'_0 x0′,然后通过后验采样得到 x t − 1 ′ x'_{t-1} xt−1′;而判别器的目标是根据输入的 x t − 1 , x t , t x_{t-1},x_t,t xt−1,xt,t来判断 x t − 1 x_{t-1} xt−1是从真实加噪过程中得到的还是模型模拟出来的结果。
可以看到,生成器需要输入 x t , z , t x_t,z,t xt,z,t,相比于DDPM多引入了一个随机latent code变量z,并且直接输出 x 0 ′ x_0^{'} x0′。作者认为引入 z z z可以使得建模出来的去噪分布能够更复杂以及multimodal。
- 为什么不直接输出 x t − 1 ′ x_{t-1}^{'} xt−1′? 因为 x t x_t xt在不同时刻扰动程度不同,直接用单个网络预测 x t − 1 ′ x_{t-1}^{'} xt−1′很难,不如直接预测无噪声的 x 0 x_0 x0;
- 什么不直接训练一个直接去生成样本的GAN,而是采用这种逐步去噪的模式?主要是因为GAN存在"训练不稳定"+“模型崩塌”+ “判别器容易过拟合” + 一些其他原因。相比之下,DiffusionGAN将生成的过程拆分多步,每一步都比较简单。此外diffusion过程能够平滑数据分布,判别器也不容易过拟合. 【多样性更好 + 更稳定】
总结:DDPM之所以要这么多的采样步长,是为了使得去噪过程 q ( x t − 1 ∣ x t ) q(x_{t-1}|x_t) q(xt−1∣xt)为高斯分布。如果采样步长较大,那么 q ( x t − 1 ∣ x t ) q(x_{t-1}|x_t) q(xt−1∣xt)的分布就复杂了,而DiffusionGAN就用一个GAN去直接学习这个分布,从而减少采样步长,提升推理速度。
此外还有从其他角度分析的工作,比如DDIM不限制扩散过程是一个马尔科夫链,使得其在采样时可以采用更小的采样步数来加速生成过程(采样一个子序列),详情请见扩散模型之DDIM。
4、潜在扩散模型与条件生成模型 - Stable Diffusion
High-Resolution Image Synthesis with Latent Diffusion Models
虽然目前已经存在一些方法来减少扩散模型的采样步骤数,比如上文提到的DiffusionGAN和DDIM,但要训练一个不错的扩散模型还是需要大量的GPU资源,这主要是因为模型的训练与推理过程都基于像素空间进行。除此之外,作为一类生成式模型,扩散模型应该拥有条件建模能力(即根据输入的条件信息生成对应的图像,例如文本、语义掩码等)。
为了解决这两个问题,Stable Diffusion分别提出了两种解决措施:首先将模型从像素空间迁移到特征空间中,去除掉不必要的高频和细节信息,在主要的语义层面进行扩散过程;其次引入条件建模,采用Cross-Attention操作将条件信息嵌入到生成去噪过程中。
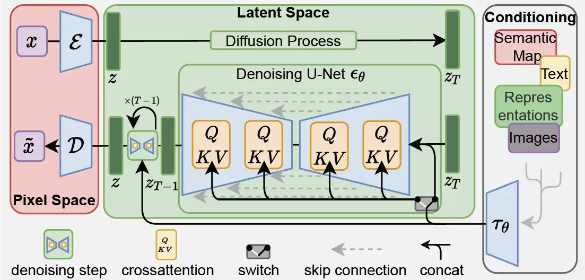
感知图像压缩
为了使扩散模型不在高分辨率的图像空间中进行训练与推理,Stable Diffusion额外引入一个感知图像压缩模型,其实也就是自编码器。自编码器包括一个编码器和一个解码器,其中编码器负责将图像x压缩到一个潜在表征 z z z(latent representation),解码器则是将这个潜在表征重构到图像空间(上图中的 ε \varepsilon ε和 D D D)。
自编码器在训练时引入了KL约束和VQ约束,并保留图像的空间维度
在引入自编码器后,扩散模型就只需要在表征空间 z z z中进行训练和推理,其空间维度是将原像素空间下采样了 f = 2 m f=2^m f=2m倍。
这类将扩散模型在特征空间中训练与推理的方法也称为LDM(Latent Diffusion Model)
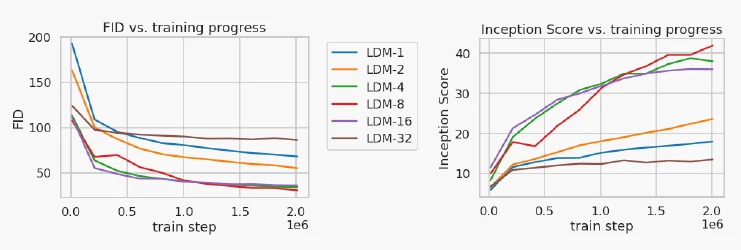
上面的实验展示了不同采样倍率的LDM在训练时的收敛情况,可以看到当下采样倍率过大和过小时效果都不太好,在4-16之间的效果较好。这意味着,下采样倍率过大时,图像会损失较多信息,倍率过小时包含了太多无效信息,导致收敛时间较长。
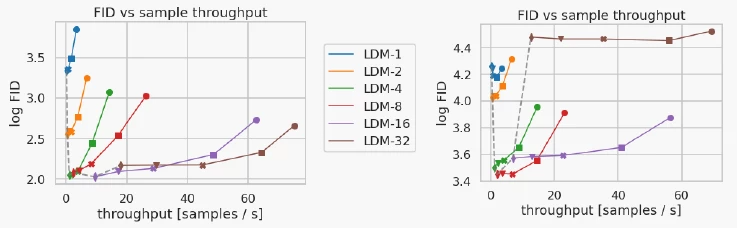
上面实验展示了不同采样倍率的LDM的推理速度(其中不同的点代表不同的采样步骤数 - 这里参考DDIM,使用了{10,20,50,100,200}),可以看到在潜在空间中推理会显著提升模型效率。
条件信息建模
为了引入条件信息,Stable Diffusion在扩散模型中(即U-Net)引入了cross-attention机制,如上面的模型结构图所示,先通过一个条件编码器将条件信息进行编码(比如文本信息就可以采用BERT这类transformer模型进行编码)。在得到条件编码信息后,每一层采用下式计算注意力:
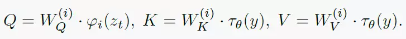
其中Q来自特征编码
z
t
z_t
zt,而K,V来自条件信息
y
y
y。通过这种方式,模型就能够在训练过程中学习到条件信息,从而在推理时根据不同的条件生成出不同的图像。
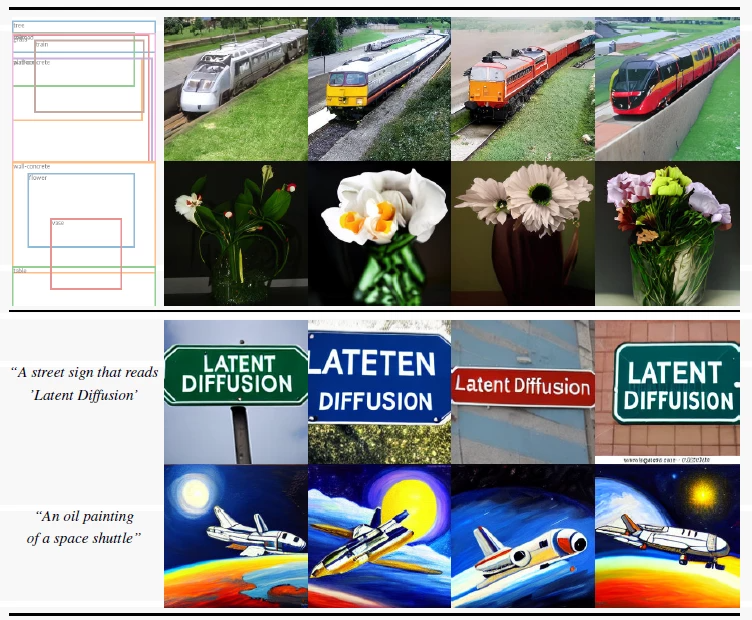
上图就是展示了Stable Diffusion对于不同的条件建模任务生成的图像(上两行是布局式图像生成, layout-to-image,下两行是文本-图像生成)。
关于Stable Diffusion更多的量化实验结果就不放在文中了,其不仅可以进行条件图像生成,还可以进行图像超分、图像重建等任务,并且表现都非常好,详情参照原文。
参考资料
[1] 强推!不愧是公认的讲的最好的【Diffusion模型全套教程】
[2] 扩散模型之DDIM。
[3] 十分钟读懂stable diffusion model
[4] Stable Diffusion原理解读