庖丁解牛——用纯python构建深度学习框架(三)
导语
在上一篇中我们简单介绍了神经网络的样子,以及通过拓扑排序和反向传播实现自动求导,但是那只是停留在概念层面,那么接下来就是用代码实现拓扑排序,以及模拟神经网络的计算过程
实现拓扑排序
先提一点,实际上在python3.9的版本上已经有了拓扑排序的功能,如果是使用python3.9版本的同学可以在python官网查看相关文档调取使用,因为我是用的是python3.8版本,所以需要手动实现拓扑排序的功能。
再理一下流程。如下图
x
,
k
1
,
b
1
x,k_1,b_1
x,k1,b1把值输入到
L
1
(
)
L_1()
L1(),之后进行非线性变换,把
L
1
(
)
L_1()
L1()的结果输出到
s
i
g
m
o
i
d
(
)
sigmoid()
sigmoid(),之后再把非线性变换结果和第二次线性变换的参数
s
i
g
m
o
i
d
(
x
)
,
k
2
,
b
2
sigmoid(x),k_2,b_2
sigmoid(x),k2,b2输入到
L
2
(
)
L_2()
L2()之后再把最后的结果和
y
y
y值输入到
L
o
s
s
(
)
Loss()
Loss()函数得到损失值,然后根据
L
o
s
s
Loss
Loss值反向传播,不断优化参数,再进行向前传播继续得到
L
o
s
s
Loss
Loss值,如此往复,最终得到模型。
这就是整个训练过程,所以现在的任务要先实现拓扑排序,为后续的向前计算和向后计算做准备。
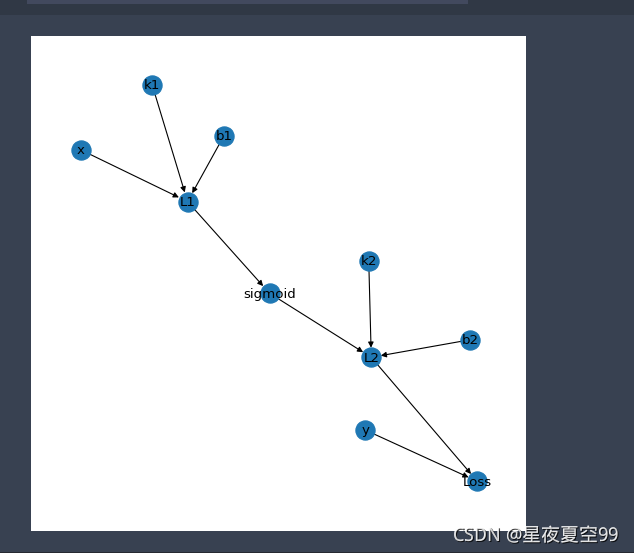
顺着上一篇的思路,建立节点与节点之间的关系,我们需要从输出和输入来建立。
#先创建一个图备用
x,k1,b1,linear1,sigmoid1,y,loss = 'x','k1','b1','linear1','sigmoid1','y','loss'
k2,b2,linear2,sigmoid2 ='k2','b2','linear2','sigmoid2'
test_graph = {
x:[linear1],
k1:[linear1],
b1:[linear1],
linear1:[sigmoid1],
sigmoid1:[linear2],
k2 : [linear2],
b2 : [linear2],
linear2:[sigmoid2],
sigmoid2:[loss],
y:[loss]
}
}
那么首先我们要理清各个节点的关系,找出有输入的 I (Input)节点,和有O(Output)输出的节点,以及只有OONI(Only Output No Input)输出没有输入的节点即外缘节点,并用列表存储记录
all_nodes_have_inputs = []
all_nodes_have_outputs = []
all_nodes_only_have_outputs_no_inputs = []
通过对test_graph的此参数观察我们我可以清楚,有输出的O节点是字典的键,那么I节点就是字典的值。求解OONI节点的话我们可以通过集合的差集来求得。
在这里因为字典的值是字典,我们需要用到python自带的reduce函数,目的是得到的数据为列表,具体用法可以到python的官方文档查看
from functools import reduce
import random
#创建一个列表用来存储排序后的结果
sorted_list = []
all_nodes_have_inputs = reduce(lambda a, b: a + b,list(graph.values()))
all_nodes_have_outputs = list(graph.keys())
all_nodes_only_have_outputs_no_inputs = set(all_node_have_outputs) - set(all_nodes_have_inputs)
数据准备完成之后,开始进行拓扑排序
大致思路是先找到OONI节点,然后记录删除,再在删除后的图中一种重复之前的工作,直到最后一个节点
# 如果OONI节点存在,那么就随机选取一个
if alL_nodes_only_have_outputs_no_inputs:
node = random.choice(list(all_nodes_only_have_outputs_no_inputs))
# 记录存储OONI节点
sorted_nodes.append(node)
# 在原字典中删除OONI节点
graph.pop(node)
这样我们的大致流程就写好了,因为我们需要不断的寻找、记录和删除节点,直至原字典没有任何数据,所以需要用一个while循环。下面我们就用函数来封装一下拓扑排序的代码。
def topologic(graph):
sorted_node = []
while graph:
all_nodes_have_inputs = reduce(lambda a, b: a + b,list(graph.values()))
all_node_have_outputs = list(graph.keys())
all_nodes_only_have_outputs_no_inputs = set(all_node_have_outputs) - set(all_nodes_have_inputs)
if all_nodes_only_have_outputs_no_inputs:
node = random.choice(list(all_nodes_only_have_outputs_no_inputs))
sorted_node.append(node)
#最后一个节点Loss节点是没有输出的,所以不在字典的key上,删除最后一个OONI节点
#Loss也就被删除了,所以该if语句是把Loss节点或者说最后一个节点添加到sorted_list中
if len(graph) == 1:
sorted_node += graph[node]
graph.pop(node)
else:
raise TypeError('This graph has circle, which cannot get topological order')
return sorted_node
#下面测试一下效果
topologic(test_graph)
>>> ['k2',
'b1',
'y',
'x',
'b2',
'k1',
'linear1',
'sigmoid1',
'linear2',
'sigmoid2',
'loss']
可以看到结果是严格按照我们的预期,实际这也展示了我们的计算过程。
x
,
y
,
k
1
,
b
1
,
k
2
,
b
2
x,y,k_1,b_1,k_2,b_2
x,y,k1,b1,k2,b2这些都是我们预先得到的数据,或是设置的参数,然后就是把相关参数和数据带依次带入到
L
1
(
)
−
>
S
i
g
m
o
i
d
1
(
)
−
>
L
2
(
)
−
>
S
i
g
m
o
i
d
2
(
)
−
>
L
o
s
s
(
)
L_1()->Sigmoid_1()->L_2()->Sigmoid_2() ->Loss()
L1()−>Sigmoid1()−>L2()−>Sigmoid2()−>Loss(),实际上这也是正向传播的过程。
得到拓扑排序的函数之后我们就要用节点来表示各个量。
# 首先创建一个节点类
class Node:
def __init__(self, inputs,outputs):
self.inputs = inputs
self.outputs = outputs
# 那么我们的节点就可以实例化了
node_x = Node(inputs = None,outputs = [node_linear])
node_k = Node(inputs = None,outputs =[node_linear])
node_b = Node(inputs = None,outputs =[node_linear])
node_y = Node(inputs = None,outputs =[node_loss])
node_linear = Node(inputs = [node_x, node_k, node_b],outputs =[node_sigmoid])
node_sigmoid = Node(inputs = [node_linear],outputs =[node_loss])
node_loss = Node(inputs = [node_y,node_sigmoid],outputs =None)
实际上这段代码不论是看上去还是运行都不是很好的代码。所以我们要优化一下。
那么我们可以按照上面拓扑图的形式,在我们实例化节点的时候只需要写出它的输入节点就可了,第二级的输入节点就是第一级的输出节点,所以可以这样优化一下代码
class Node:
def __init__(self, inputs= []):
self.inputs = inputs
self.outputs = []
for node in inputs:
node.outputs.append(self)
node_x = Node()
node_k = Node()
node_b = Node()
node_y = Node()
node_linear = Node(inputs = [node_x, node_k, node_b])
node_sigmoid = Node(inputs = [node_linear])
node_loss = Node(inputs = [node_y,node_sigmoid])
下面我就需要一些代码来生成图
# 创建一个列表,其中元素都是需要输入参数的节点
need_feed_value_nodes = [node_x, node_y, node_k, node_b]
from collections import defaultdict
# 该模块可以让我们通过上面的节点,也就是外援节点生成图
computing_graph = defaultdict(list)
while need_feed_value_nodes:
n = need_feed_value_nodes.pop(0)
if n in computing_graph:continue
for m in n.outputs:
computing_graph[n].append(m)
need_feed_value_nodes.append(m)
#这样我们就可以用拓扑排序来进行排序了
print(topologic(computing_graph))
>>>[<__main__.Node at 0x2232c0cf4c0>,
<__main__.Node at 0x2232c0cf1c0>,
<__main__.Node at 0x2232c0cfd30>,
<__main__.Node at 0x2232c6ae160>,
<__main__.Node at 0x2232c0cf400>,
<__main__.Node at 0x2232c0cfe20>,
<__main__.Node at 0x2232c0cfe50>]
打印出来的都是地址,那么我们可以在Node类中做一点手脚,让结果更清晰,同时我们也可以把上面的代码进行封装
import random
from functools import reduce
from collections import defaultdict
def topologic(graph):
"""拓扑排序"""
sorted_node = []
while graph:
all_nodes_have_inputs = reduce(lambda a, b: a + b,list(graph.values())) #所有有输入的节点
all_node_have_outputs = list(graph.keys()) #所有有输出的节点
all_nodes_only_have_outputs_no_inputs = set(all_node_have_outputs) - set(all_nodes_have_inputs)
if all_nodes_only_have_outputs_no_inputs:
node = random.choice(list(all_nodes_only_have_outputs_no_inputs))
sorted_node.append(node)
if len(graph) == 1:
sorted_node += graph[node]
graph.pop(node)
for _,links in graph.items():
if node in links:links.remove(node)
else:
raise TypeError('This graph has circle, which cannot get topological order')
return sorted_node
class Node:
"""定义一个节点类"""
def __init__(self, inputs= [],name = None):
"""初始化参数"""
self.inputs = inputs
self.outputs = []
self.name = name
for node in inputs:
node.outputs.append(self)
def __repr__(self):
"""打印时,打印节点名"""
return f'Node:{self.name}'
def convert_feed_dict_to_graph(feed_dict):
"""根据外缘节点生成图"""
need_expand = [n for n in feed_dict]
computing_graph = defaultdict(list)
while need_expand:
n = need_expand.pop(0)
if n in computing_graph:continue
for m in n.outputs:
computing_graph[n].append(m)
need_expand.append(m)
return computing_graph
#定义节点
node_x = Node(name = 'x')
node_k = Node(name = 'k')
node_b = Node(name = 'b')
node_y = Node(name = 'y')
node_linear = Node(inputs = [node_x, node_k, node_b],name = 'linear')
node_sigmoid = Node(inputs = [node_linear],name = 'sigmoid')
node_loss = Node(inputs = [node_y,node_sigmoid],name = 'loss')
#外缘节点
need_feed_value_nodes = [node_x, node_y, node_k, node_b]
print(topologic(convert_feed_dict_to_graph(feed_dict)))
>>>[Node:y, Node:x, Node:k, Node:b, Node:linear, Node:sigmoid, Node:loss]
到这一步我们就基本实现了神经网络计算之前的工作!!!