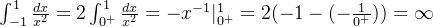第五单元 用python学习微积分(三十二)无穷的处理--不定式(下)和反常积分
本文内容来自于学习麻省理工学院公开课:单变量微积分-反常积分-网易公开课
Bullseye:第一单元 用python学习微积分(一) 安装开发环境Anaconda 和 导数(上)- 1/x的导数
目录
(3)结论:式子 , 当 时是发散的,而当 p >1 时是收敛的( )
一、洛必达法则复习
1、无限比无限的情况( 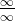 )
)
如果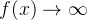 ,
, 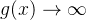 ,
, 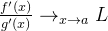 成立, 则
成立, 则 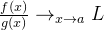 , 其中
, 其中 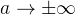 或
或 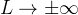 是允许的。
是允许的。
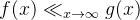 可以理解为
可以理解为 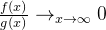 ,
, 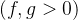
函数值排序:
增长: 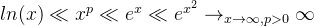
函数值排序:
减小: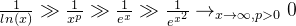
二、反常积分
1、基本概念
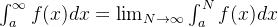
如果这个积分极限存在(这个极限有限),他就是收敛的(converges),否则就是发散的(diverges)
函数的积分收敛的情况,也就是函数曲线到x轴的面积是有限的,否则这个曲线下的面积就是无限的
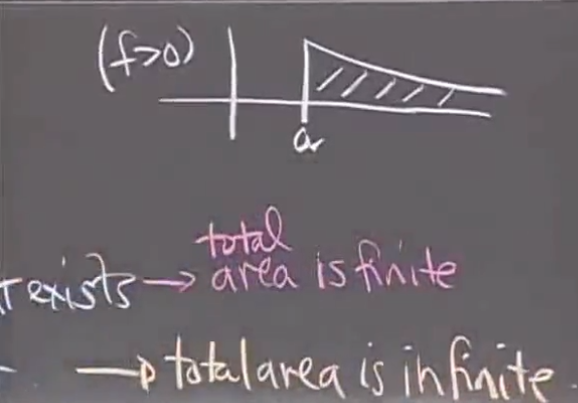
添加图片注释,不超过 140 字(可选)
2、例1
(1)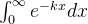 ( k > 0 )
( k > 0 )
import numpy as np
from sympy import *
import matplotlib.pyplot as plt
figure, ax= plt.subplots( 1 )
ax.set_aspect( 1 )
def DrawXY1(xFrom,xTo,steps,expr,color,label,plt, arrow =False):
yarr = []
xarr = np.linspace(xFrom ,xTo, steps)
for xval in xarr:
#print(expr.subs(x,xval), xval)
yval = expr.subs(x,xval)
yarr.append(yval)
y_nparr = np.array(yarr)
x_nparr = np.array(xarr)
length = len (xarr)
plt.plot(x_nparr, y_nparr, c=color, label=label)
if(arrow and steps > 2):
plt.arrow(float(x_nparr[0]),float( y_nparr[0]),float( x_nparr[2]-x_nparr[0]),float( y_nparr[2]-y_nparr[0]), width=.02, color = color)
def DrawXY(tFrom,tTo,steps,exprX,exprY, color,label,plt, arrow =False):
xarr = []
yarr = []
tarr = np.linspace(tFrom ,tTo, steps)
for tval in tarr:
xval = exprX.subs(t,tval)
xarr.append(xval)
yval = exprY.subs(t,tval)
yarr.append(yval)
y_nparr = np.array(yarr)
x_nparr = np.array(xarr)
length = len (xarr)
plt.plot(x_nparr, y_nparr, c=color, label=label)
if(arrow and steps > 2):
plt.arrow(float(x_nparr[0]),float( y_nparr[0]),float( x_nparr[2]-x_nparr[0]),float( y_nparr[2]-y_nparr[0]), width=.02, color = color)
x = symbols('x')
k=2
expr = np.e**(-k**2*x)
DrawXY1( 0.1,4,50,expr,color='c', label=' e**(-k**2*x)',plt = plt, arrow = True)
plt.legend(loc='lower right')
plt.show()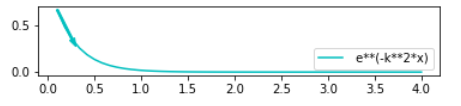
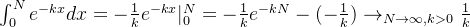
简便写法: 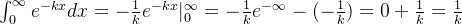
(2) 放射性粒子的平均衰减度(概率相关)
在时间T内辐射出的粒子的总数=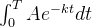 A代表某总数
A代表某总数
所能辐射出的粒子的总数=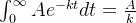
3、例2 一个概率计算中重要的常量
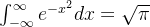
以上这些式子都是收敛的,从而告诉我们当遇到包含它们的式子时,我们能知道这些是有极限的
4、例3 1/x的p次幂 (p>0)
(1)临界情况 p=1
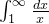
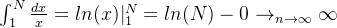
所以这个积分是发散的
x = symbols('x')
expr = 1/x
DrawXY1( 1,50,50,expr,color='c', label='1/x',plt = plt, arrow = False)
expr = ln(x)
DrawXY1( 1,50,50,expr,color='r', label='ln(x)',plt = plt, arrow = False)
plt.legend(loc='lower right')
plt.show()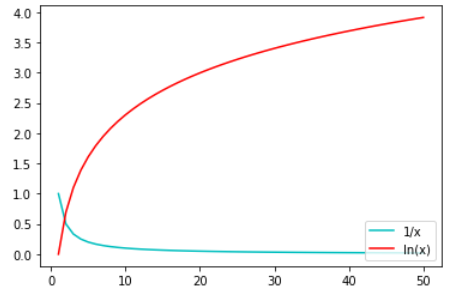
(2)
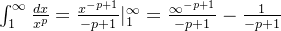
当 0<p<1时
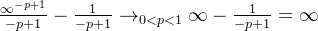
当 p>1时
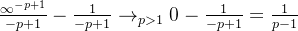
(3)结论:式子 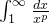 , 当
, 当 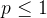 时是发散的,而当 p >1 时是收敛的(
时是发散的,而当 p >1 时是收敛的( 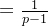 )
)
5、极限的比较
当 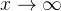 , 如果 f(x) 和 g(x) 相似(
, 如果 f(x) 和 g(x) 相似(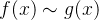 ) .....(means
) .....(means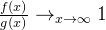 ) ,
) ,
此时 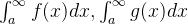 ( a 取一个很大的值 )同时收敛或同时发散
( a 取一个很大的值 )同时收敛或同时发散
6、例4
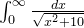
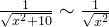
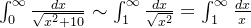
结果是发散的,所以可以忽略有限的 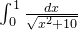 , 这里不考虑
, 这里不考虑 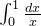 是因为这个式子是发散的和原式(
是因为这个式子是发散的和原式(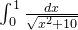 )同条件下的结果有很大的不同。
)同条件下的结果有很大的不同。
7、例5
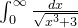
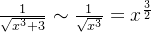
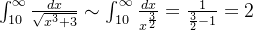 (
(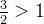 , 由例3结论 )
, 由例3结论 )
得出结论这个积分是收敛的
8、例2 - 续
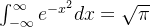
expr = np.e**(-x**2)
DrawXY1( -5,5,50,expr,color='r',label= '',plt = plt, arrow = False)
plt.legend(loc='lower right')
plt.show() 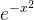 函数图形
函数图形
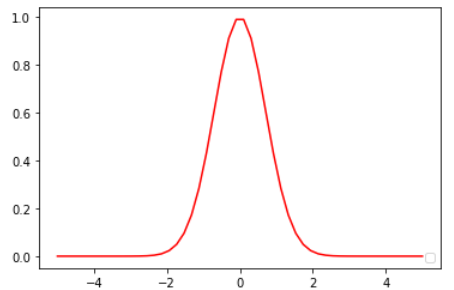
这个图形 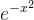 根据y轴对称
根据y轴对称
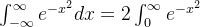
做个比较
当 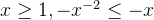
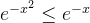
所以有
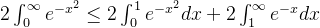
由 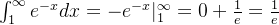 ,
,
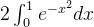 是收敛的
是收敛的
可知 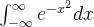 是收敛的
是收敛的
9、反常积分的第二种类型
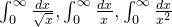
一般这些积分还是可以直接计算得到它们是收敛还是发散,但是老师提到了一个不一样的例子
错误 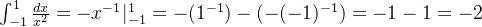 错误
错误
而函数 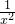 在(-1,1)区间的图形是这样的
在(-1,1)区间的图形是这样的
expr = 1/(x**2)
DrawXY1( -1,-0.1,50,expr,color='r',label= '',plt = plt, arrow = False)
DrawXY1( 0.1,1,50,expr,color='r',label= '',plt = plt, arrow = False)
plt.legend(loc='lower right')
plt.show()
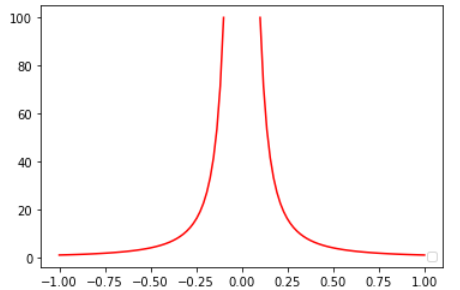
我个人觉得,这里不能直接计算这个积分,是因为在-1 到1 的范围内 x=0处是奇点 , 函数不连续。
个人觉得应该是这样计算,由于这个函数在y轴对称,