【介绍】有哪些决策树
目录
本文部分图文借鉴自《老饼讲解-机器学习》
0. 前言-决策树介绍
决策树(Decision Tree)是一种常见的机器学习方法,它基于树形结构来进行决策。
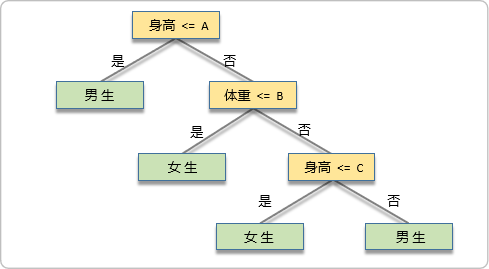
决策树在分类问题中特别有效,也可以用于回归问题。它通过将数据集划分成若干个子集,从而实现对整个数据集的预测。决策树的每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。决策树是一种直观运用概率分析的一种图解法,其目的是为了产生一棵泛化能力强,即处理未见示例能力强的决策树。
一、决策树有哪些
那么,但我们经常到到CART决策树、ID3决策树等等,对于刚接触决策树的同学是非常困惑的,下面我们详细讲讲决策树有哪些种类。
主要有以下5种常见决策树
1.ID3决策树
2. C4.5决策树,
3.C5.0决策树
4.CART分类树
5.CART回归树
但从技术角度进行分类,它们又可以分为两条支线
1.CART: classification and regression tree,分类与回归树
即CART自身包括了分类树与回归树
2.ID3系列: ID3算法,C4.5算法,C5.0算法
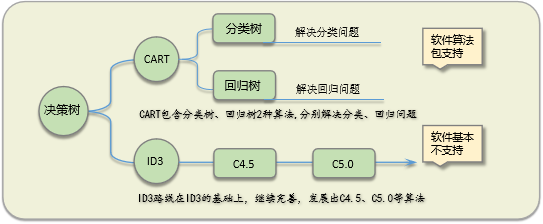
目前matlab和python软件都只实现了CART决策树,如果要实现ID3,C4.5,C5.0等,一般需要自行编写代码进行实现
二、各种决策树详细解释
下面我们详细介绍各种决策树,同时区分各种决策树的特性
2.1 ID3决策树
ID3决策树是由Ross Quinlan发明的用于决策树的算法,该算法建立在奥卡姆剃刀的基础上:越是小型的决策树越优于大的决策树。
ID3决策树只支持枚举变量。每个节点选择一个变量,按该变量所有可能取值分叉。
下面是一棵ID3决策树:
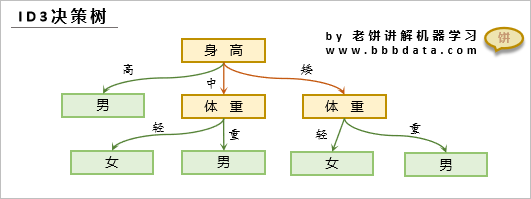
ID3算法使用信息增益来选择属性,以构建决策树。它首先计算当前例子集合的熵,然后计算每个属性的信息增益,并选择信息增益最大的属性作为当前节点的测试条件。然后,算法将根据该属性的值将例子集合划分为两个子集,并递归地在每个子集上执行相同的过程,直到满足停止条件为止。
ID3决策树的优点:
1.算法简单,通俗易懂。
2.可以处理离散型数据。
3.能够利用信息增益来选择属性,选择信息增益最大的属性作为根节点,从而帮助算法有效地进行决策。
ID3决策树的缺点:
1.无法处理缺失值,需要对缺失值进行预处理。
2.只能处理离散值,无法处理连续值。对于连续值的处理需要先进行离散化处理,这个过程可能会带来信息的损失。
3.存在偏向于选择取值较多的特征的问题。因为特征取值越多,说明划分的越细,不确定性越低,信息增益则越高。
4.容易出现过拟合。为了避免过拟合问题,可以裁剪决策树,去掉一些不必要的子树或叶节点,或者设置决策树的最大深度。
2.2 C4.5决策树
C4.5决策树是ID3决策树算法的改进版,由Ross Quinlan提出。C4.5决策树在以下几方面对ID3算法进行了改进:
1.用信息增益率来选择属性,克服了用信息增益选择属性时偏向选择取值多的属性的不足。
2.在树构造过程中进行剪枝。
3.能够完成对连续属性的离散化处理。
4.能够处理不完整数据。
C4.5决策树算法的优点是产生的分类规则易于理解且准确率较高。但是,在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,从而导致算法的低效。
C4.5决策树算法的优点包括:
1.产生的分类规则易于理解,准确率较高。
2.能够完成对连续属性的离散化处理。
3.能够处理不完整数据。
4.在树构造过程中进行剪枝。
C4.5决策树算法的缺点包括:
1.算法相对ID3要复杂许多
2.在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,从而导致算法的低效。
2.3 C5.0决策树
C5.0决策树是对C4.5算法的改进,主要在以下几个方面进行了优化:
1.引入了分支度(branching degree)的概念,用信息增益率作为判断优先划分属性的标准。分支度的计算公式是指,若某划分属性S将样本T划分成n个子集T1,T2,...Tn,则此属性S的分支度就等于:每个分支子集Ti的个数ci,出于样本总个数t,然后再乘以log2ci/t,然后再把各个分支的计算值加起来。
2.C5.0和C4.5可以处理数值型数据,处理方式核心思想:将数值从小到大排序,对每两个数值间进行试探切割,算出Gain Ratio,找到最大的那个切割Gain Ratio,进行切割离散化。
3.剪枝:C4.5和C5要对决策树进行剪枝,剪枝的目的是为了避免过拟合问题。这两种算法的剪枝方法是Bottom-Up从下往上剪枝,也就是说,先利用训练集把决策树建好。然后从下往上砍树。
总的来说,C5.0决策树在保持准确性的同时更注重算法效率,在处理数据时具有更强的泛化能力
2.4 CART分类树
CART(Classification And Regression Trees)决策树是一种常见的机器学习方法,可以用于分类和回归。CART决策树在做分类时,称为CART分类树。
下面是一棵CART分类树:
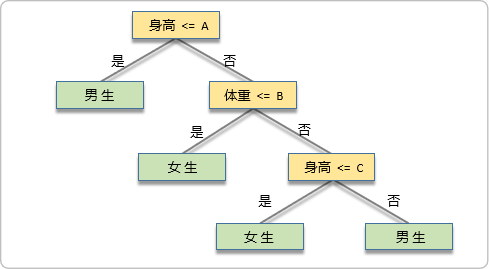
CART分类树采用递归的方式将数据空间划分为不重叠的矩形,其分类过程如下:
1.选择一个自变量和一个值,将数据空间划分为两部分,一部分的所有点都满足该条件,另一部分的所有点都不满足该条件。
2.对每个划分点,计算其基尼系数,并选择划分后基尼系数最小的点进行划分。
3.将整个数据空间划分为多个子集,每个子集都采用相同的划分方式,直到满足停止条件为止。
4.对于每个叶子节点,采用多数表决的方式进行分类,即选择该节点中占比最大的类别作为该节点的预测类别。
CART分类采用叶子节点中样本数最多的类别作为该节点的预测类别。
CART决策树的详细构建过程可参考《老饼讲解|【原理】CART决策树构建过程详细讲解》
2.5 CART回归树
CART回归树是与CART分类树一样,仍然是一棵二叉树,只是最终叶子节点是一个数值
下面是一棵CART回归树,它通过身高、年龄预测体重(体重是连续变量)
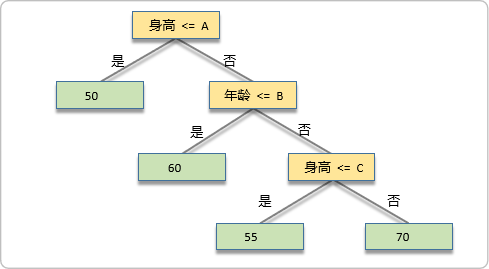
CART决策树回归过程如下:
1.用树模型做回归问题,每一个叶子节点都输出一个预测值,预测值一般是该叶子节点所含训练集样本的输出均值。
2.CART回归树的特征和分割点选择准则:CART回归树常用均方误差(Mean Squared Error,MSE/L2)最小化准则作为特征和分割点的选择方法。
需要注意的是,CART决策树回归的过程与分类树类似,但采用不同的评价标准。对于回归问题,CART采用均方误差作为评价标准,通过最小化每个节点中的观测值和平均值之间的误差平方和来选择最佳的分割点。
CART决策树的优点:
1.可以处理非线性关系:CART决策树可以捕捉变量之间的非线性关系,而不需要事先假设数据之间的关系。
2.易于解释:CART决策树生成的规则很容易理解,有助于业务决策和解释。
3.可以进行特征选择:CART决策树可以通过计算每个特征的信息增益或基尼指数来选择重要的特征,这对于高维数据集非常有用。
4.可以处理大规模数据集:CART决策树算法可以处理大规模数据集,并且在处理大数据集时相对较快。
CART决策树的缺点:
1.容易过拟合:CART决策树容易过度拟合训练数据,导致泛化能力较差。为了避免过拟合,需要进行剪枝或者使用正则化方法。
2.对缺失值和异常值敏感:CART决策树对缺失值和异常值比较敏感,可能导致生成的决策树不稳定。需要对数据进行预处理,如填充缺失值或删除异常值。
3.可能创建偏向的树:如果某些类别的样本数量过大,CART决策树可能会创建偏向这些类别的树。需要对数据进行平衡处理或者使用适当的采样技术。
如果觉得本文有帮助,点个赞吧!