【数据结构】 堆排序与TopK问题详解
在学习完堆的创建后,就轮到了标题的两个问题
这两个问题在实际生活中会有比较强的实际问题解决能力
先分别解释一下
- 堆排序:
运用堆的思想进行排序,时间复杂度为O(NlogN) - TopK:
从一大堆数据中选择K个最大或最小的数据,我们简称tTopK
堆的创建,关于堆的详情请点击。
堆排序:
思想:
假设我们有一个小堆为N个数,先在要对其排序,那么这个小堆适合什么排序呢?
答案是降序
绝大部分同学可能都会认为是升序,
因为最上边的元素是最小的,我们将第一个固定住,在对其后边N-1个再次进行建堆,就可以完美得到一个升序的数组,
注意:
但是我们忽略了建堆的时间复杂度为O(lNogN),对N个数进行建堆,比冒泡排序有过之而无不及,所以我们不会去用这样一个华而不实的方法
所以我们小堆其实更适合
降序,将建堆之后的第一个元素与数组末尾进行交换,再对这N-1个数进行向下调整算法,每调整一次时间复杂度为O(N),以此类推,再将第一个与倒数第二个交换…
代码实现:
我们既然进行排序,就要有一个待排序的数组,我们将数组传给堆排序,同样,当然也需要知道数组个数
int arr[] = { 5,7,3,9,1,2,6,0 };
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
然后我们就可以对这个数组进行建堆了,你的升降序也是根据你建的堆来进行的,要仔细区分
对于建堆,我们有两种方法
自上而下建堆:
这也是我们最容易想到的一种
利用循环将数组变成小堆
for (int child = 0; child < size; child++)
{
AdjustUp(arr, child);
}
自下而上建堆:
这是我们推荐的一种,因为他的时间复杂度小于上一种方式(从最后一个叶子节点的父节点开始,少了最后一层,而最后一层接近N/2个节点),同时,他只会用到向下调整算法,在进行排序时也只会用到向下算法,故很适合我们使用
int parent = (size - 1 - 1) / 2;
while (parent)
{
AdjustDown(arr, size, parent);
parent--;
}
AdjustDown(arr, size, parent);
排序代码:
//因为是小堆,排序降序
int child = size - 1;
for (int i = child; i > 0; i--)
{
Swap(&arr[0], &arr[i]);
AdjustDown(arr, i, 0);
}
for (int i = 0; i < size; i++)
{
printf("%d ", arr[i]);
}
源代码:
heap.c与heap.h我们用到的依然是开头链接处的代码,这里我们直接引用他们
void HeapSort(int* arr, int size)
{
//建堆:向下与向上
向下
//for (int child = 0; child < size; child++)
//{
// AdjustUp(arr, child);
//}
//向上
int parent = (size - 1 - 1) / 2;
while (parent)
{
AdjustDown(arr, size, parent);
parent--;
}
AdjustDown(arr, size, parent);
//因为是小堆,排序降序
int child = size - 1;
for (int i = child; i > 0; i--)
{
Swap(&arr[0], &arr[i]);
AdjustDown(arr, i, 0);
}
for (int i = 0; i < size; i++)
{
printf("%d ", arr[i]);
}
}
int main()
{
int arr[] = { 5,7,3,9,1,2,6,0 };
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}
TopK:
思想:
关于TopK我们有两种实现方法:
- 将
N个数据进行建堆,在依次Pop掉堆顶,得到K个最大或最小的数据,但这种方式显然代价太大,且如果N太大,malloc会开辟不出来这么多数据的数组 - 我们先建一个
K个数的堆,假设为小堆,那么此时还是问同学们一个问题,小堆适合选出最大的还是最小的呢?
解:
答案是最大的,
因为我们在建好一个小堆后,需要拿堆顶的元素与N个数据中剩下的元素比较,又因为我们是小堆,所以当一个元素大于栈顶元素时,那个元素就会进入堆,我们进行向下排序,那个元素就会下沉,直到选出K个最大的数据,
如果建立大堆的话,假设堆顶是K个数中最大的数据,就会挡在前边,另外几个次大的数据就会入不了堆,造成错误
代码实现:
首先创建一个文件,里面有很多的数据
void CreatData()
{
FILE* fin = fopen("pata.txt", "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
//write data
srand(time(NULL));
for (int i = 0; i < 10000000; i++)
{
int x = (rand() + i) % 10000000;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}
注意:
创建完文件后我们要进入文件,改变几个数值(改变为超过取模的数字,这样我们就可以验证我们的代码准确性)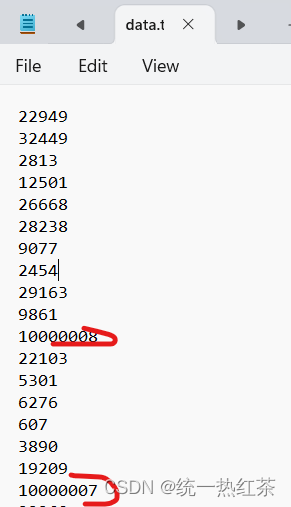
创建一个大小为K的堆
FILE* fout = fopen(filename, "r");
if (fout == NULL)
{
perror("fopen fail");
return;
}
// 建一个k个数小堆
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{
perror("malloc error");
return;
}
将大数据中的前N个放入堆中
// 读取前k个,建小堆
for (int i = 0; i < k; i++)
{
fscanf(fout, "%d", &minheap[i]);
AdjustUp(minheap, i);
}
依次读取,直到读取完毕并打印数据
int x = 0;
while (fscanf(fout, "%d", &x) != EOF)
{
if (x > minheap[0])
{
minheap[0] = x;
AdjustDown(minheap, k, 0);
}
}
for (int i = 0; i < k; i++)
{
printf("%d ", minheap[i]);
}
printf("\n");
free(minheap);
fclose(fout);
源代码:
void CreatData()
{
FILE* fin = fopen("pata.txt", "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
//write data
srand(time(NULL));
for (int i = 0; i < 10000000; i++)
{
int x = (rand() + i) % 10000000;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}
void TopK(char* filename, int k)
{
FILE* fout = fopen(filename, "r");
if (fout == NULL)
{
perror("fopen fail");
return;
}
// 建一个k个数小堆
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{
perror("malloc error");
return;
}
// 读取前k个,建小堆
for (int i = 0; i < k; i++)
{
fscanf(fout, "%d", &minheap[i]);
AdjustUp(minheap, i);
}
int x = 0;
while (fscanf(fout, "%d", &x) != EOF)
{
if (x > minheap[0])
{
minheap[0] = x;
AdjustDown(minheap, k, 0);
}
}
for (int i = 0; i < k; i++)
{
printf("%d ", minheap[i]);
}
printf("\n");
free(minheap);
fclose(fout);
}
int main()
{
//粘贴时注意先将创建数据的函数放出来,单独修改后再TopK
//CreatData();
TopK("data.txt", 5);
return 0;
}
有问题及时询问博主,25小时高强度冲浪