通俗易懂的双线性插值
双线性插值这个算法和公式，着实有点晦涩难懂，花了我很长时间。现在用图文并茂的方法，把我的理解记录一下。
一、先看一下线性插值法
学双线性插值法之前，先把线性插值法学懂，这个很重要，因为后面需要直接套公式。
上个图（网上盗的……）：
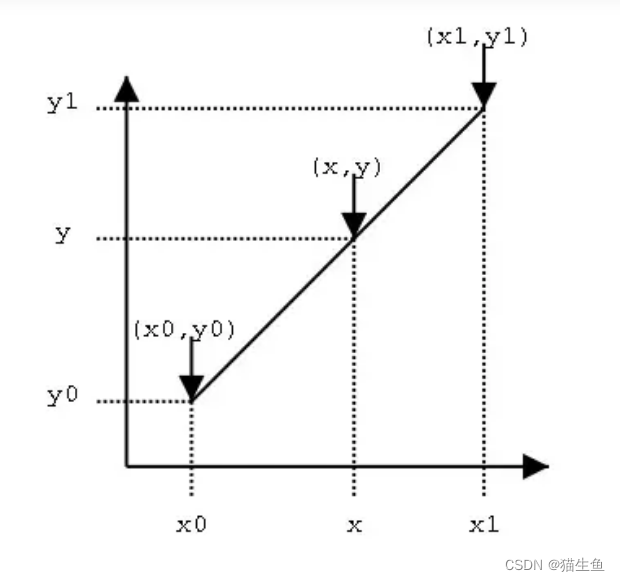
假设我们已知坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间内某一位置x在直线上的值。根据上图中所示，我们从两点式直线方程:
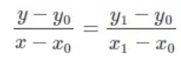
将这方程化解一下可得：
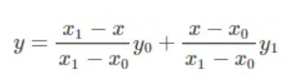
这个是有公式的，直接套就行：‘两点式方程公式’：已知直线1上的两点P1(x1, y1)、P2(x2, y2), (x1≠x2)，那么可得：(y-y1)/(y2-y1)=(x-x1)/(x2-x1)。
二、再来看双线性插值法
知道了线性插值法学了之后，再来看双线性插值法。
要是不乐意看公式的，可以直接跳到图片演示，示例能看懂也行。
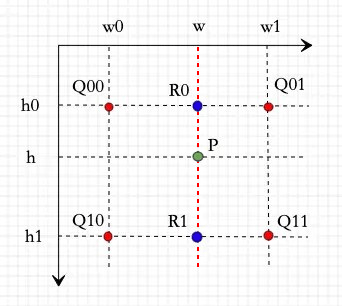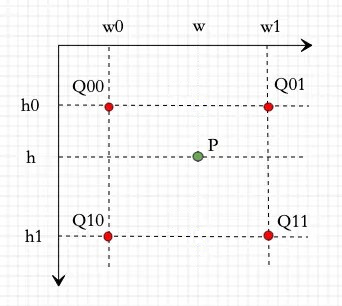
下面是关于双线性插值的经典说明图例：
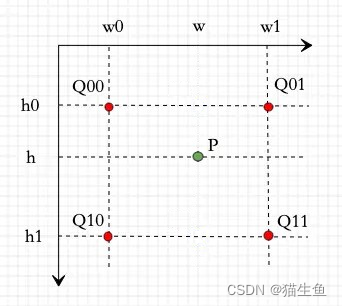
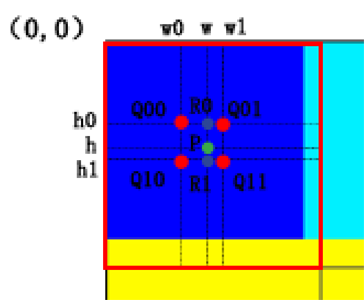
首先，图中有5个像素点：Q00, Q01, Q10, Q11, P。
其中四个红色点Q是原图的点，绿色点P则是目标图片上像素点在原图上的投影。
四个红色点Q就是投影点P的四周最近的点，通过这四个红色点Q，可以计算出投影点P的像素值，这样目标图片上的像素点点值就求出来了。
三、目标图的点如何投影到原图上？
已知：
1. 原图的高、宽、通道数为：height_src, width_src, channel_src。
2. 目标图的高、宽、通道数为：height_dst, width_dst, channel_src。因为通道要相同嘛
可以计算出投影公式为：h = h_dst * height_src / height_dst, w = w_dst * width_src / width_dst。
举个例子：原图大小是33， 目标图大小是99， 目标图的中心点坐标是(4,4)。按照上面的投影公式，计算目标图的中心点投影到原图中心点的坐标为：h = 4 * 3 / 9 = 1.3333, w = 4 * 3 / 9 = 1.3333，中心点坐标为(1.3333, 1.3333)。
这里就发现一个问题了，原图的大小为3*3，中心点坐标应该是(1,1)啊，公式计算出来的明显不一样。
之所以会出现这个情况，原因是每个像素点实际上是一个边长为1的正方形，所以对于坐标为(h,w)的像素点，它的中心其实是(h+0.5,w+0.5)。
所以精确的算法应该是：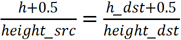
和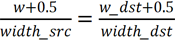 
，转换一下得到正确的投影公式：
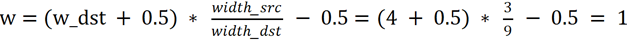
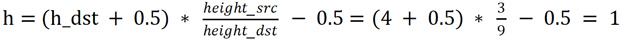
四、如何插值计算得到投影点的像素值？
已知：
1. 四个红色点Q的坐标值为：h0, h1, w0, w1，它们的像素值为f(Q00), f(Q01), f(Q10), f(Q11)。
2. 投影点P的坐标值h, w。
思路是：每个Q点的像素值乘以各自的权重，然后想加得到投影点P像素值。
Q点跟P点的距离越近，它的权重就越大。
双线性插值给出的算法很简单粗暴：先在横轴方向上进行两次线性插值计算，然后在纵轴方向上进行一次插值计算。
求横轴上的两次线性插值计算，就是求R0和R1这两个蓝色点的像素值。
再通过R0和R1两点的像素值，求得P点的像素值。
因其上已经求过线性插值的公式为：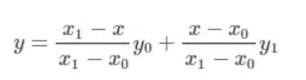
，现在直接代入就可以了。
具体计算如下：
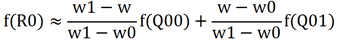
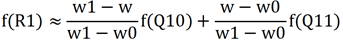
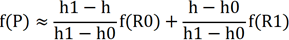
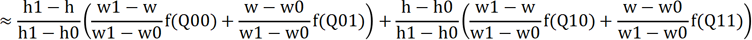
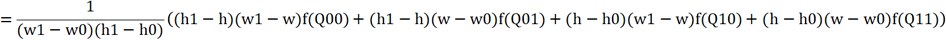
前面有说过，四个红色点Q是投影点P四周最近的点，点P又是目标图片上的一个坐标，其实相当于是一个宽度为1的像素方块。
所以w1-w0=1, h1-h0=1。
即公式又可以写成：
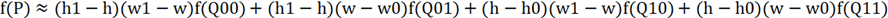
再设置u和v，令：u=h-h0, v=w-w0，公式又可以写成：
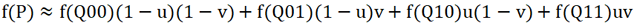
到这一步，双线性插值的原理和公式就全部讲完了，再用一个图片来演示一下，融会贯通。
五、图片演示
现在有如上这样一张图片，大小为20 * 20，通道3。现在想通过双线性插值的算法，将它变成3 * 3大小的图片。
先做一个坐标轴，记得图片的原坐标(0,0)是在左上角的，将整个图片分为3 * 3等份。
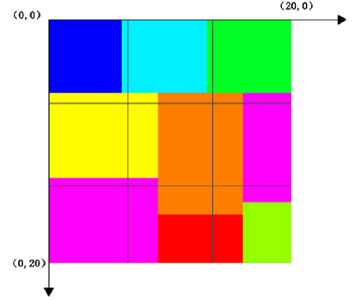
一份一份来计算：
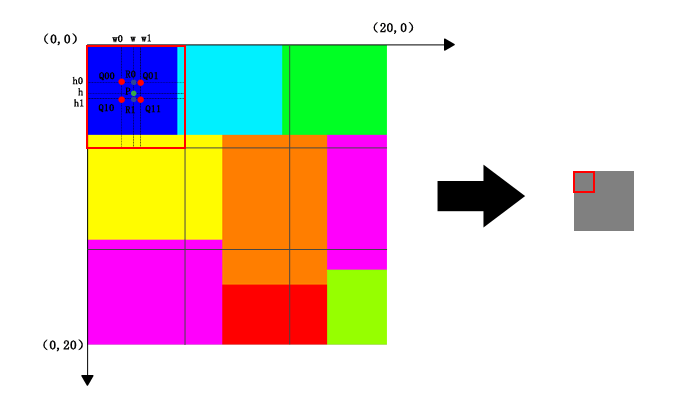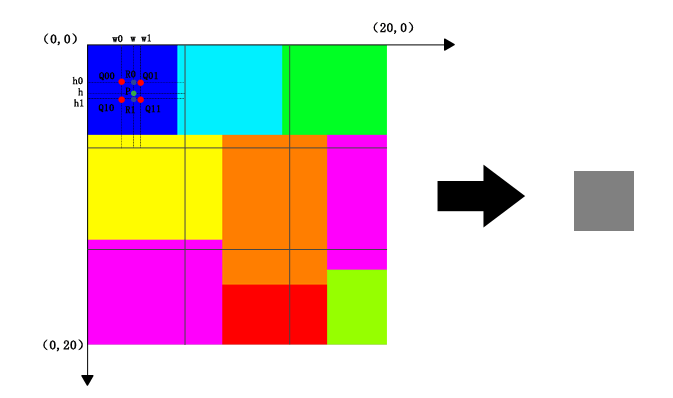
那么来计算一下第一份的P点坐标。因为P点其实是目标图的像素点的投影。那么也就是(0,0)的投影，代入中心对齐后的算法公式，应该是：
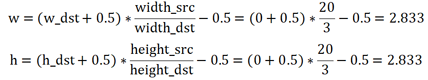
那么P点的坐标值应该是(2.833, 2.833),Q作为离P点最近的坐标点，坐标应为：h0=2, h1=3, w0=2, w1=3。
到这里，就可以求出u和v的值来，u=h-h0=0.833, v=w-w0=0.833。
又因为我们这个图片是RGB的彩色图，通道为3，所以对应到3*3目标图上时，每一个通道的值都要计算。
现在我们可以来代入公式了。
已知：
1. Q的颜色值为：Q00(0, 0, 255), Q01(0, 0, 255), Q10(0, 0, 255), Q11(0, 0, 255)。
2. u=0.833, v=0.833。
代入公式可得：
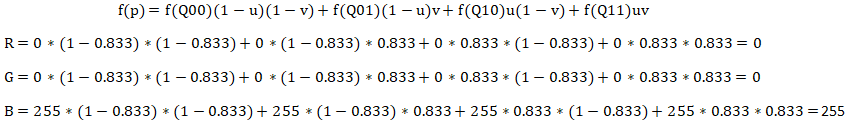
可求得P点对应的目标图的坐标值为(0, 0, 255)。
以此类推，可讲3*3的目标图求出为：
代码
from PIL import Image
import numpy as np
import math
def bilinear_interpolate(src, dst_size):
height_src, width_src, channel_src = src.shape # (h, w, ch)
height_dst, width_dst = dst_size # (h, w)
"""
中心对齐，投影目标图的横轴和纵轴到原图上
"""
ws_p = np.array([(i + 0.5) / width_dst * width_src - 0.5 for i in range(width_dst)], dtype=np.float32)
hs_p = np.array([(i + 0.5) / height_dst * height_src - 0.5 for i in range(height_dst)], dtype=np.float32)
"""找出每个投影点在原图横轴方向的近邻点坐标对"""
# w_0的取值范围是 0 ~ (width_src-2)，因为w_1 = w_0 + 1
ws_0 = np.clip(np.floor(ws_p), 0, width_src - 2).astype(int)
print(ws_p, ws_0)
"""找出每个投影点在原图纵轴方向的近邻点坐标对"""
# h_0的取值范围是 0 ~ (height_src-2)，因为h_1 = h_0 + 1
hs_0 = np.clip(np.floor(hs_p), 0, height_src - 2).astype(int)
dst = np.zeros(shape=(height_dst, width_dst, channel_src), dtype=np.float32)
us = hs_p - hs_0
vs = ws_p - ws_0
_1_us = 1 - us
_1_vs = 1 - vs
for h in range(height_dst):
h_0, h_1 = hs_0[h], hs_0[h] + 1 # 原图的坐标
for w in range(width_dst):
w_0, w_1 = ws_0[w], ws_0[w] + 1 # 原图的坐标
for c in range(channel_src):
dst[h][w][c] = src[h_0][w_0][c] * _1_us[h] * _1_vs[w]\
+ src[h_0][w_1][c] * _1_us[h] * vs[w]\
+ src[h_1][w_0][c] * us[h] * _1_vs[w]\
+ src[h_1][w_1][c] * us[h] * vs[w]
return dst
im_path = 'test.bmp'
image = np.array(Image.open(im_path))
image2 = bilinear_interpolate(image, (3, 3))
image2 = Image.fromarray(image2.astype('uint8')).convert('RGB')
image2.save('out.png')