【计算机视觉】角点检测(Harris、SIFT)
Harris
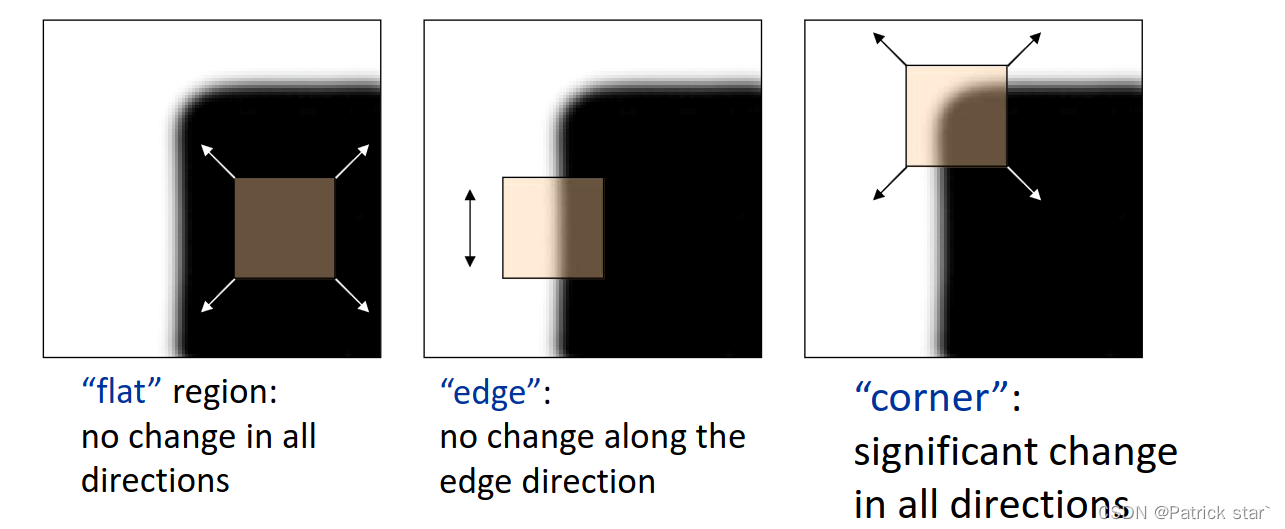
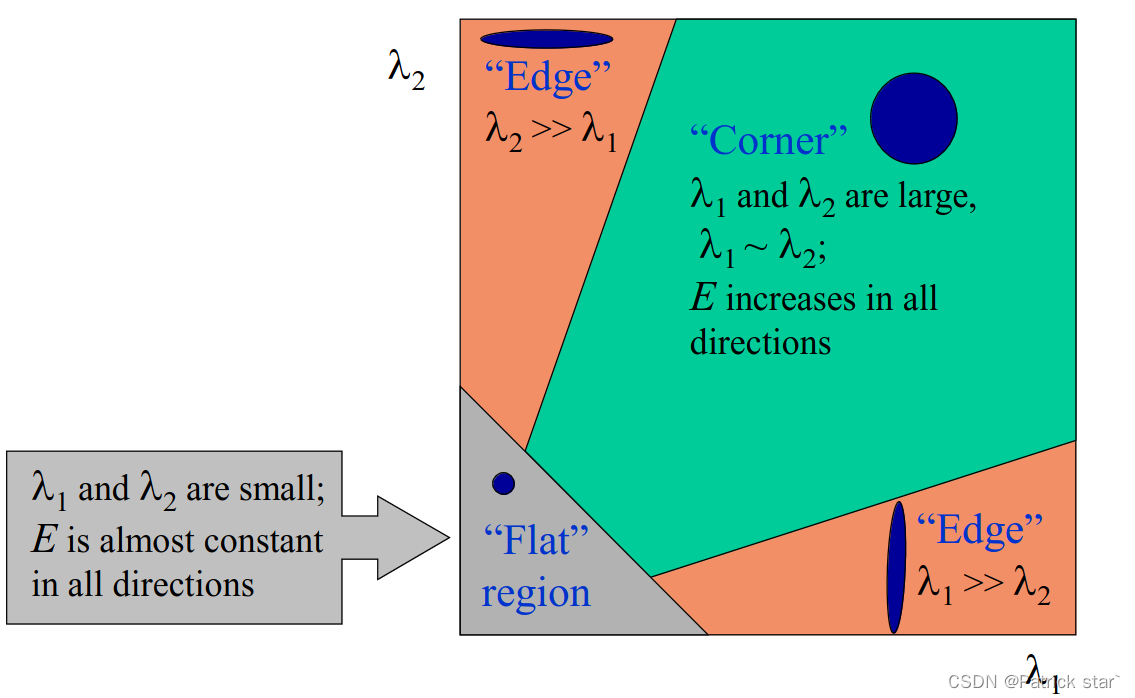
角点指的是窗口延任意方向移动,都有很大变化量的点。
用数学公式表示为:
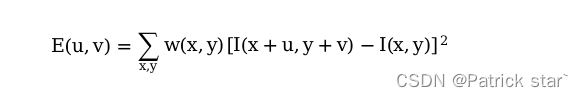
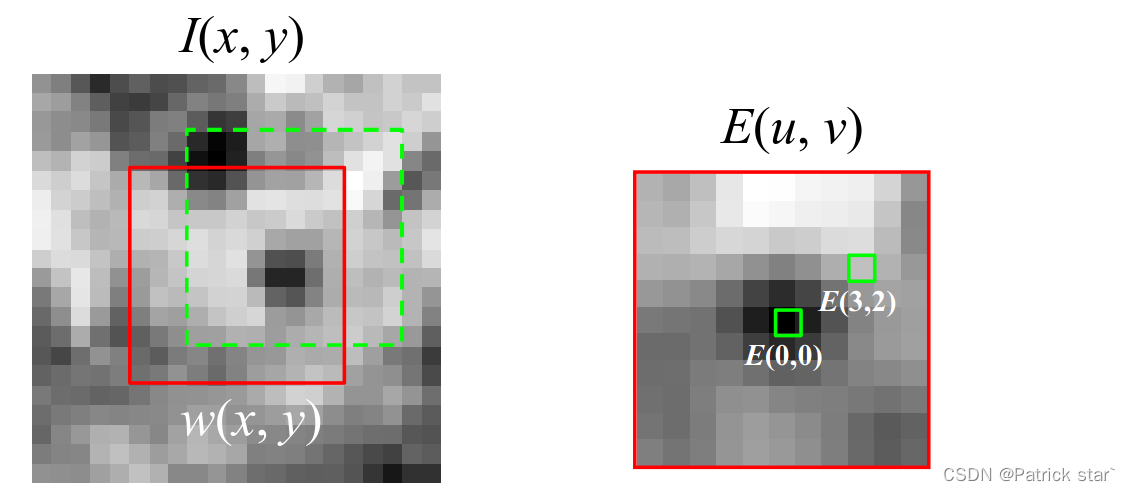
E(u,v)反映的移动后窗口的差异,w(x,y)为每个像素的点权值,I(x+u,y+v)是移动的像素值,I(x,y)是移动前的像素值。
将E(u,v)进行泰勒展开,直接建立E(u,v)和u,v的联系
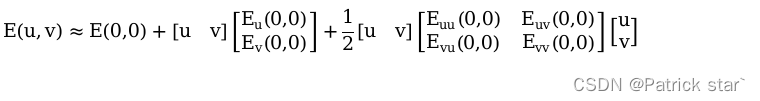
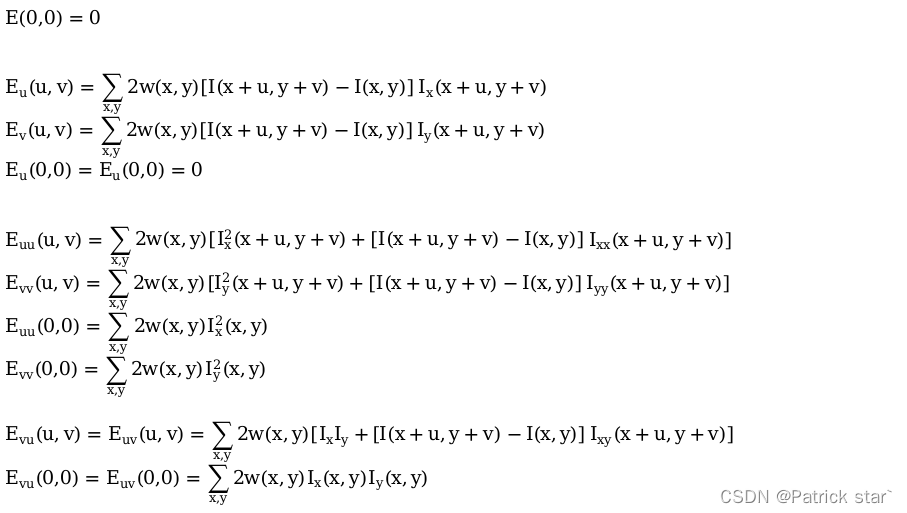
最终:
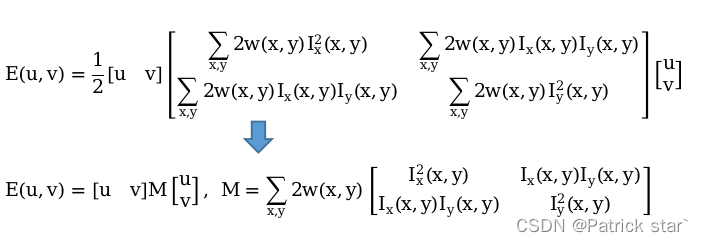
M称为二阶矩矩阵(second moment matrix)
若 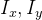 互不影响:
互不影响:
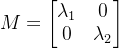
假设 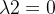 :
:
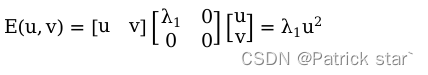
只有在u方向上变化是E才会变,因此只有 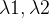 都不为0时(x,y)才是角点。
都不为0时(x,y)才是角点。
若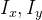 相关可以通过正交化变成前面的形式:
相关可以通过正交化变成前面的形式:
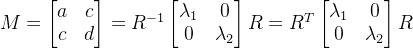
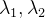 就反映了点在某个方向上的变化率,之后当
就反映了点在某个方向上的变化率,之后当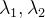 都很大时,该点才是角点。
都很大时,该点才是角点。
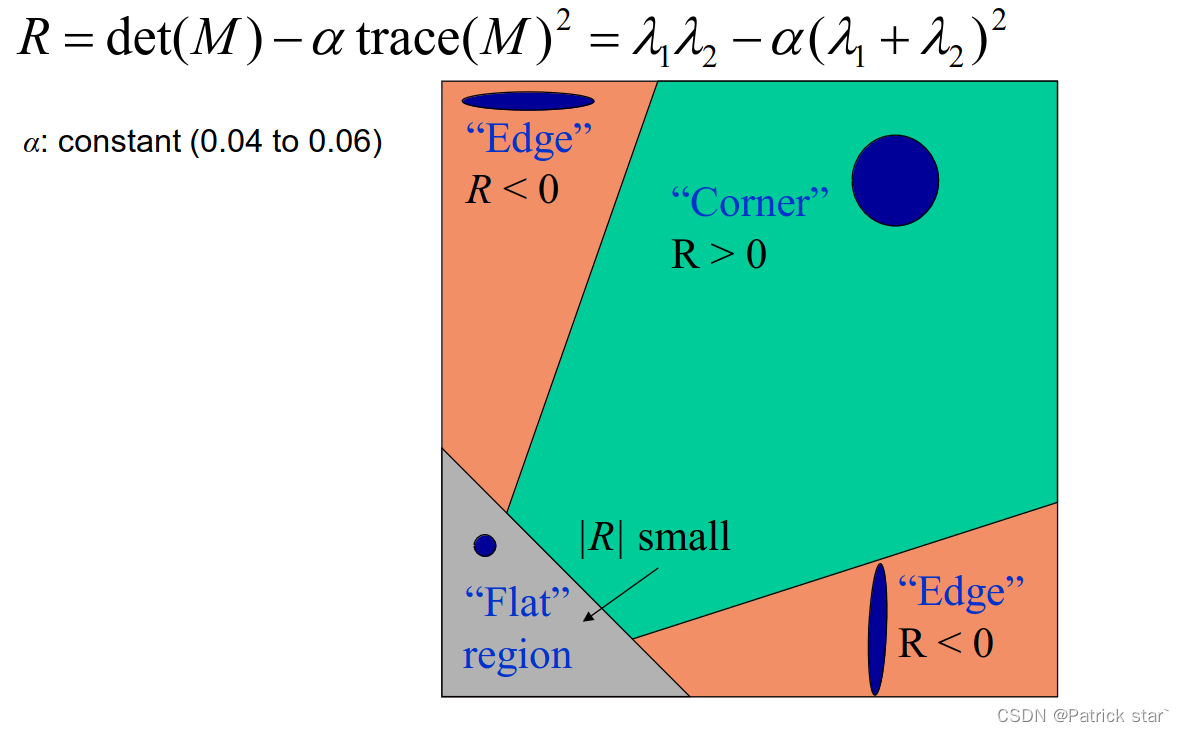
为了减少计算可以用R来判定是否为角点
SIFT
Harris角点检测不具有尺度不变性,窗口大小不同,响应的结果也不同。
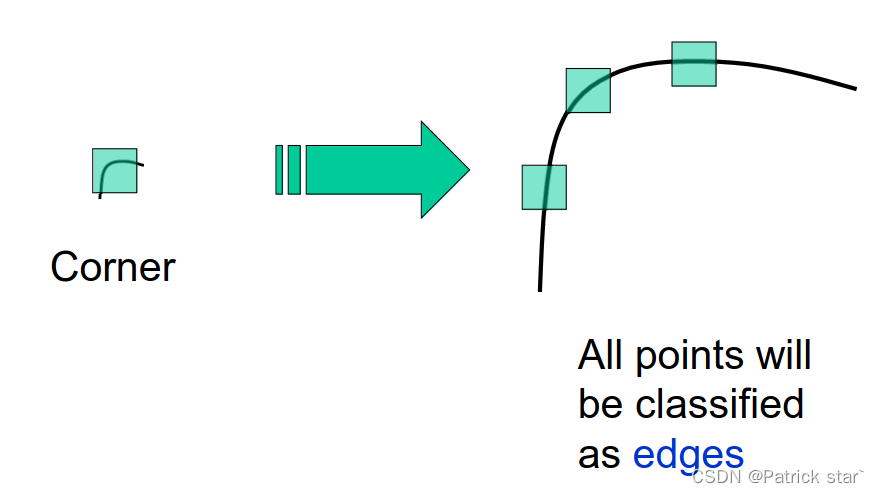
所谓的尺度不变性,指的是提取器能够对不同的尺度下的同一个点,有比较大的响应值。
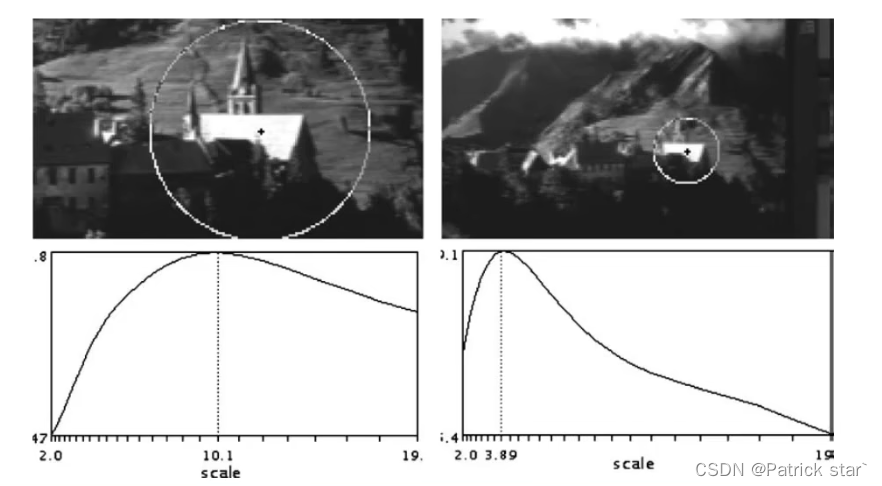
接下来,介绍的SIFT就是具有尺度不变性的特征提取算法。
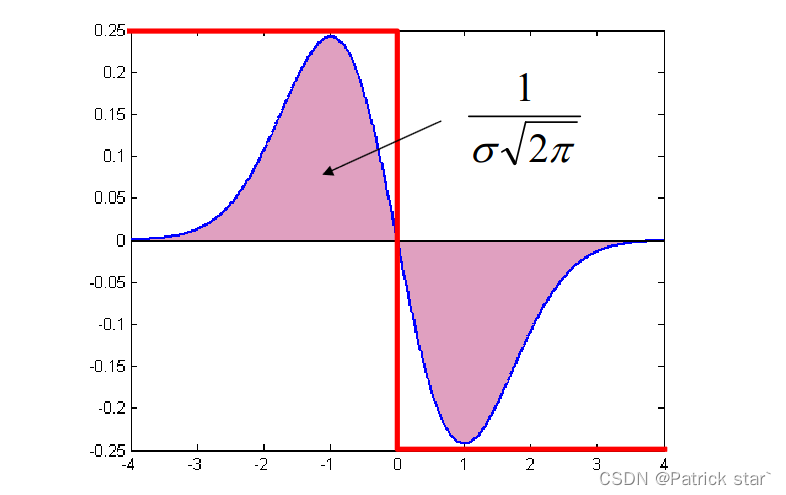
在边缘提取的时候,用高斯一阶导对信号进行卷积,响应值最大的就是边界。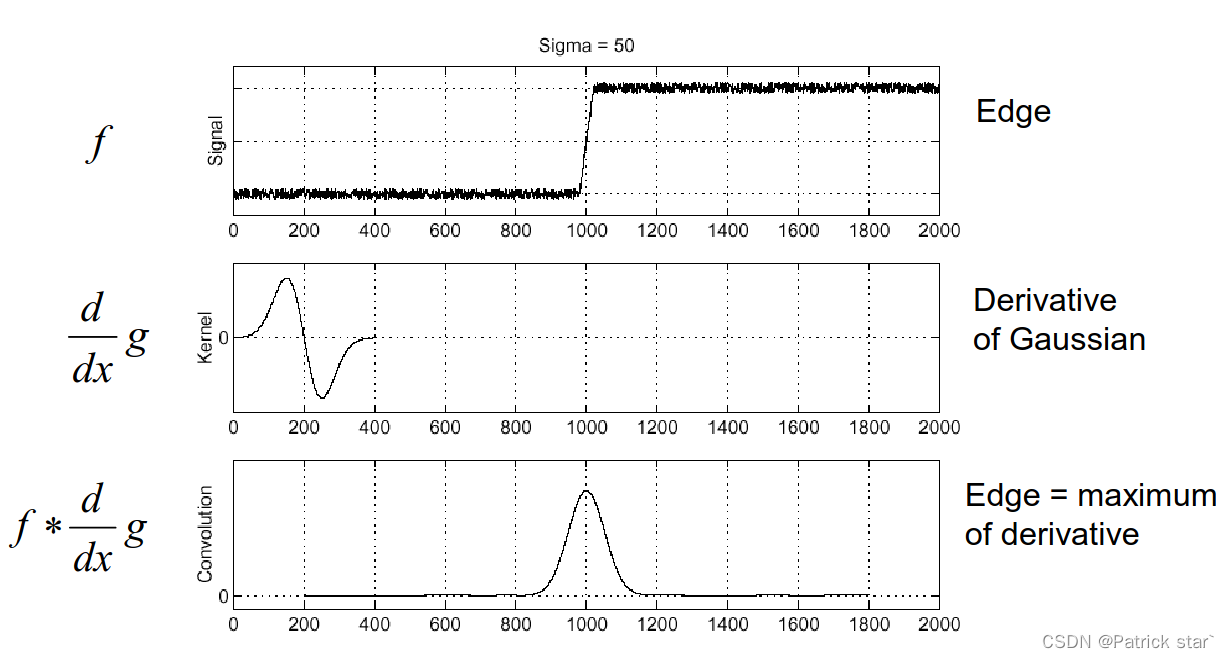
如果用高斯二阶导对信号进行卷积,0点就是边界点(二阶导等于0的点,对应一阶导的极值点)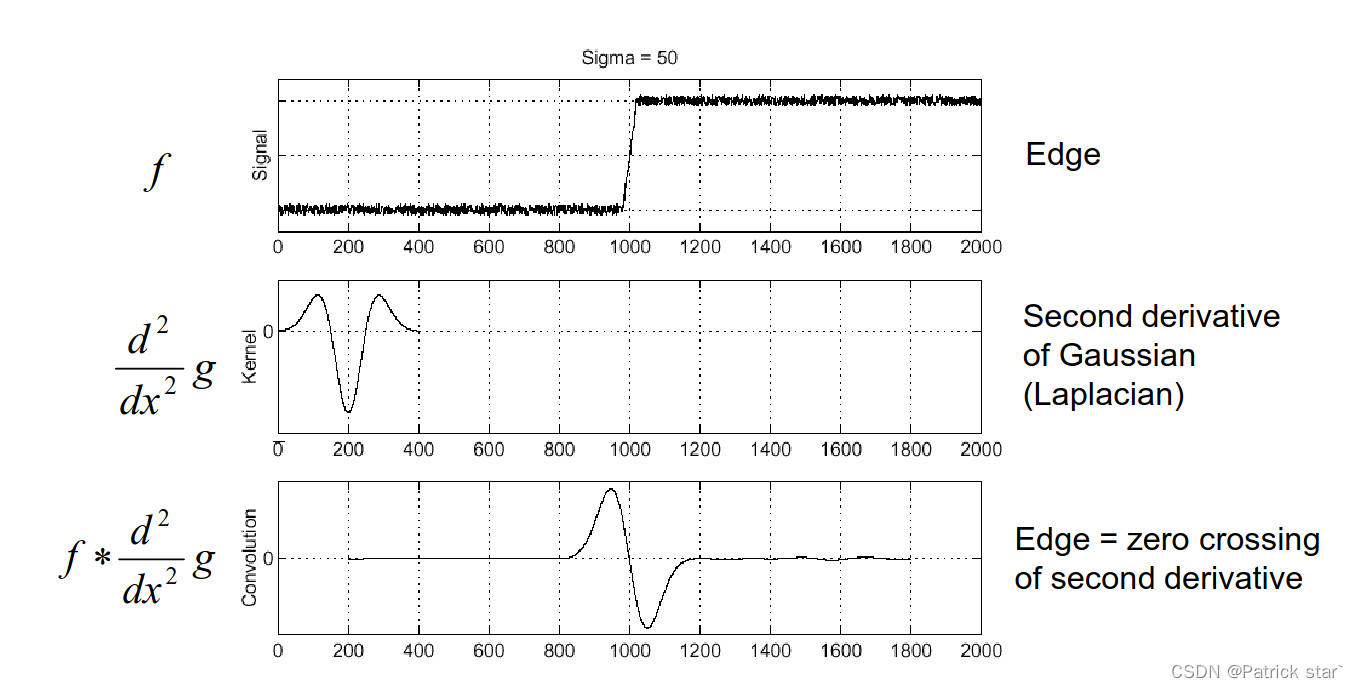 如果用高斯二阶导在不同的信号上进行卷积,当信号宽度与高斯滤波核匹配的时候,就能得到绝对值最大的信号,这样就建立了尺度和滤波核之间的联系。
如果用高斯二阶导在不同的信号上进行卷积,当信号宽度与高斯滤波核匹配的时候,就能得到绝对值最大的信号,这样就建立了尺度和滤波核之间的联系。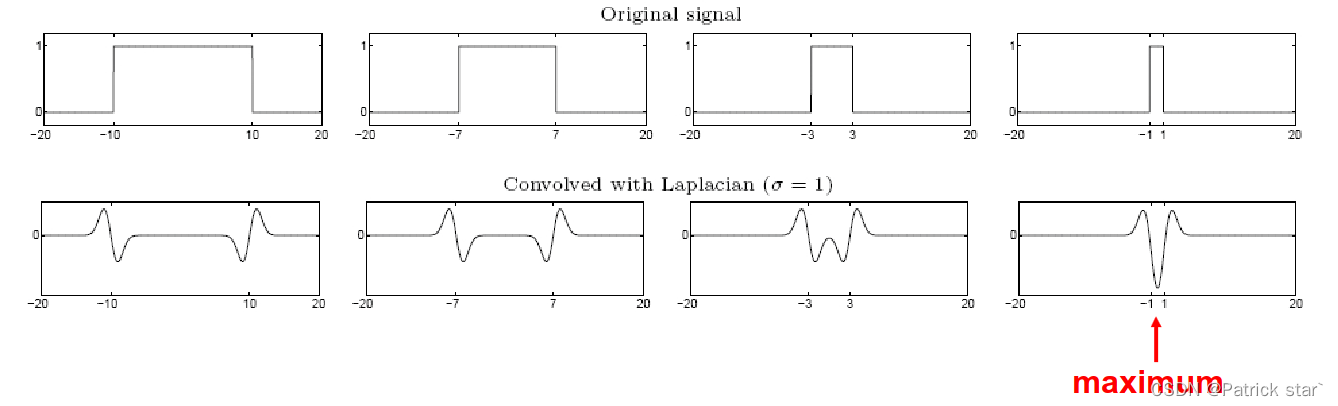
用不同的Laplacian对同一个信号进行卷积的时候,随着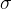 的增大,响应值会越来越不明显。
的增大,响应值会越来越不明显。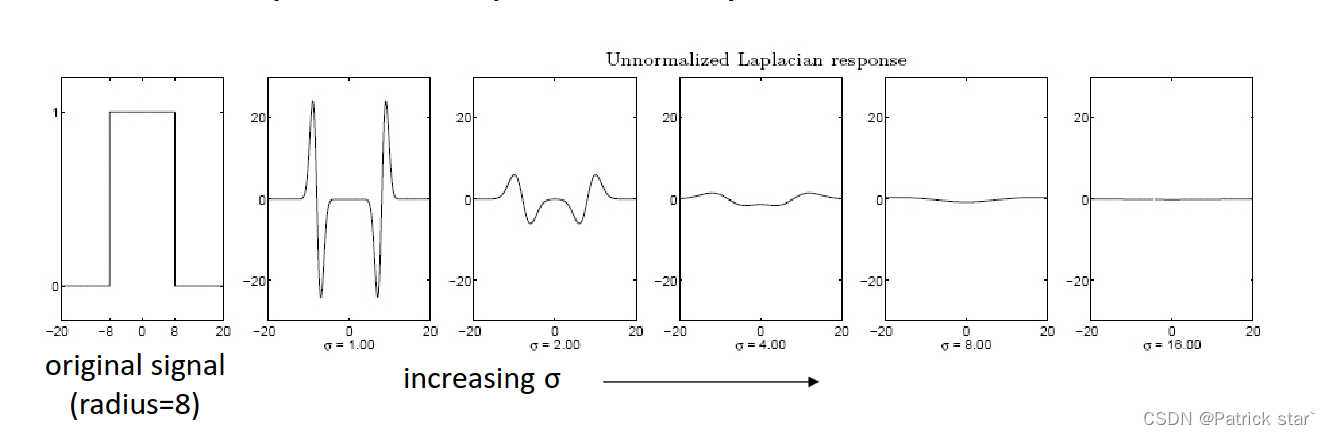
因为 作为分母,
作为分母, 越来越大,卷积后的信号值就会越来越小 ,对于一阶偏导需要对卷积后的信号补偿
越来越大,卷积后的信号值就会越来越小 ,对于一阶偏导需要对卷积后的信号补偿 ,对于二阶偏导需要对卷积后的信息补偿
,对于二阶偏导需要对卷积后的信息补偿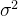 ,将响应值固定在一个尺度上。
,将响应值固定在一个尺度上。
补偿之后,就能用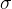 反映尺度
反映尺度
二维Laplacian高斯卷积核如下图所示: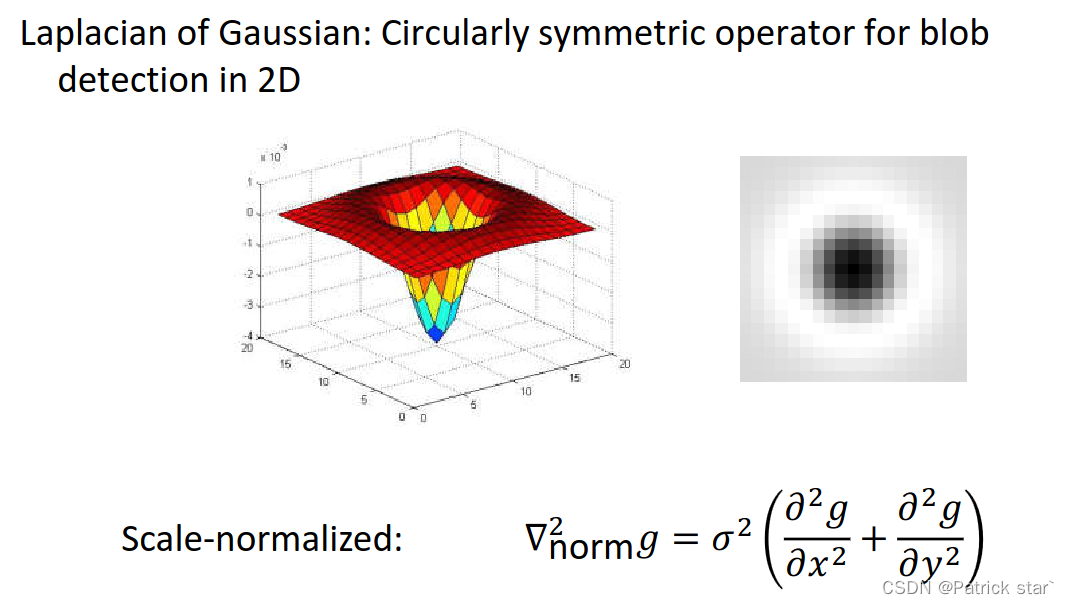
当半径值正好与Laplacian为0的值匹配上的时候,响应值最大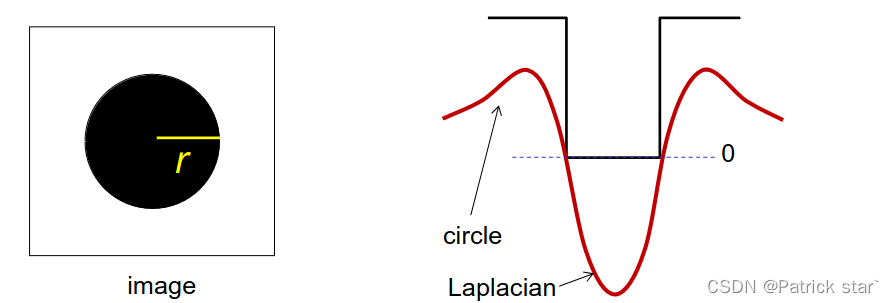
假设这个圆是二进制的,简单来说就是找到一个合适的laplacian卷积核,卷积之后使得laplacian卷积核中小于0的部分权值为0,laplacian大于0的部分权值为1。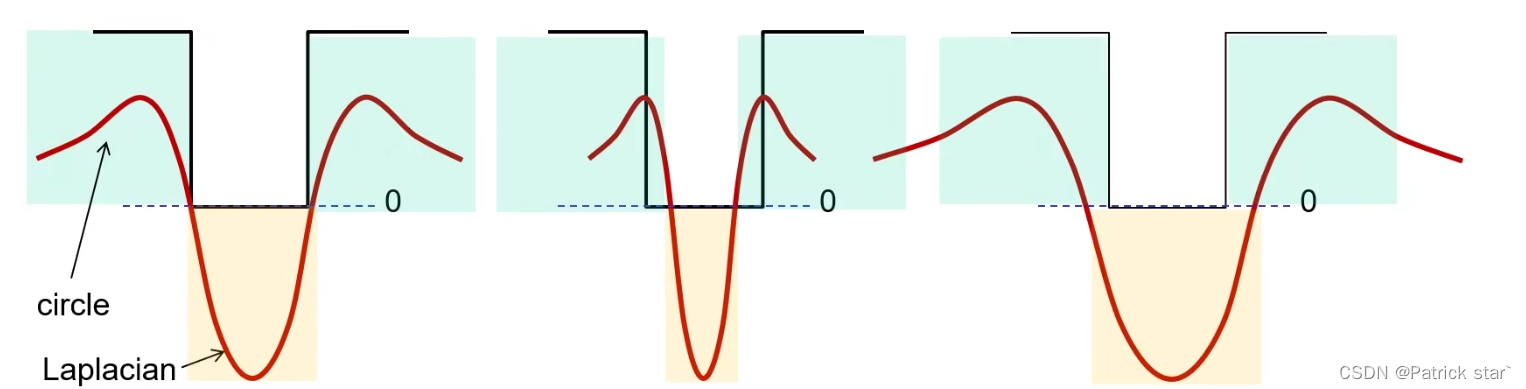
找到合适的laplacian卷积核,它的 与信号半径有对应关系
与信号半径有对应关系

SIFT使用的是DoG模版(两个高斯模版的差分),拥有和Laplacian类似的特性
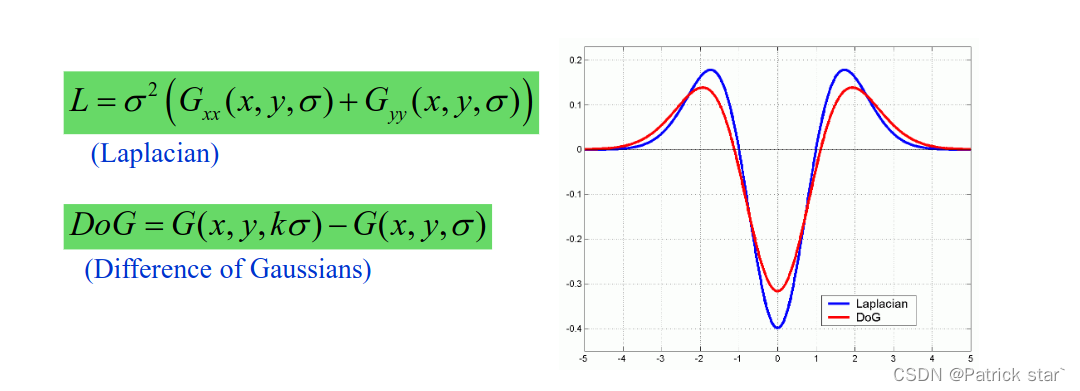
一般而言,随着 的增大,窗口也会变大,Laplacian每一次都会在原图进行卷积,卷积的成本就会增大。而DoG是利用高斯卷积核来做的,可以通过对较小
的增大,窗口也会变大,Laplacian每一次都会在原图进行卷积,卷积的成本就会增大。而DoG是利用高斯卷积核来做的,可以通过对较小 的卷积核卷积得到较大
的卷积核卷积得到较大 的卷积核,减小卷积成本。
的卷积核,减小卷积成本。
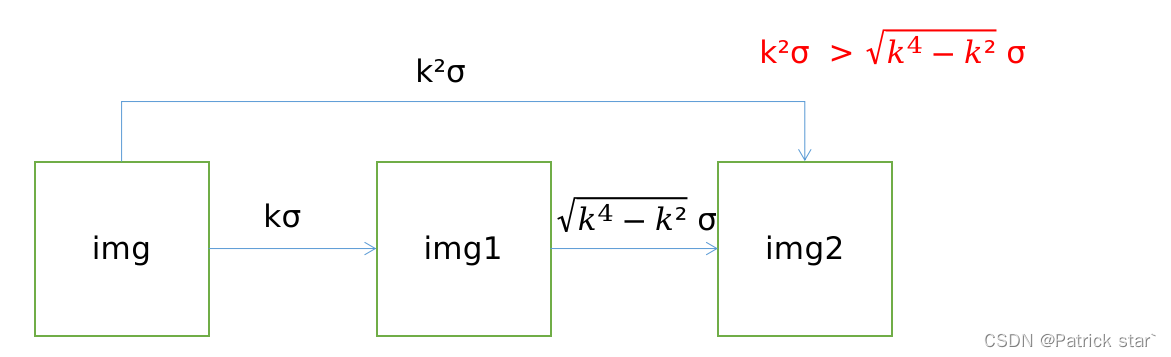
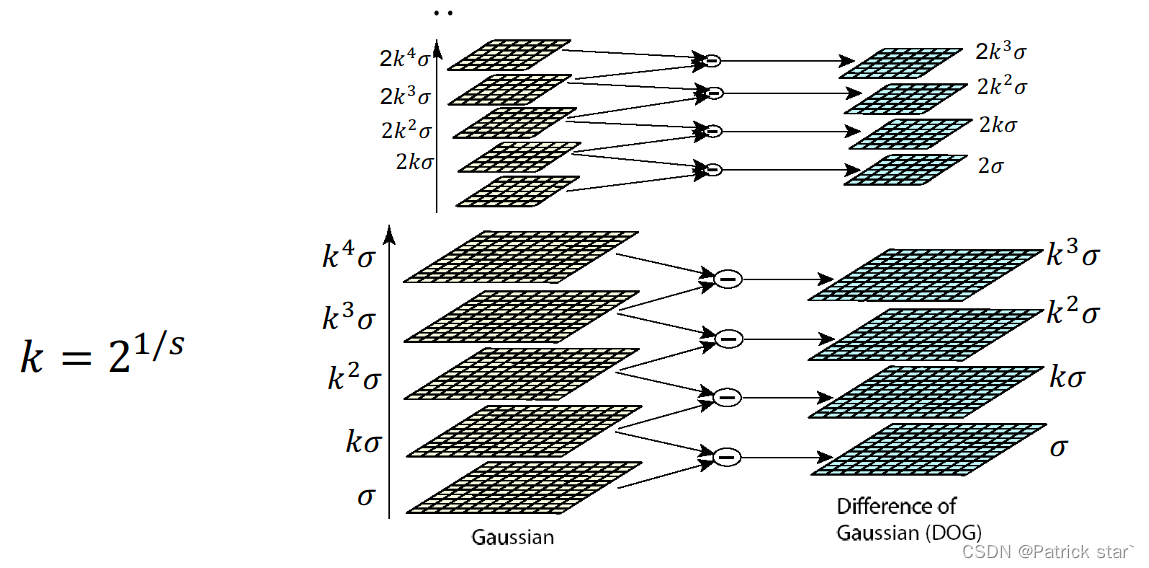
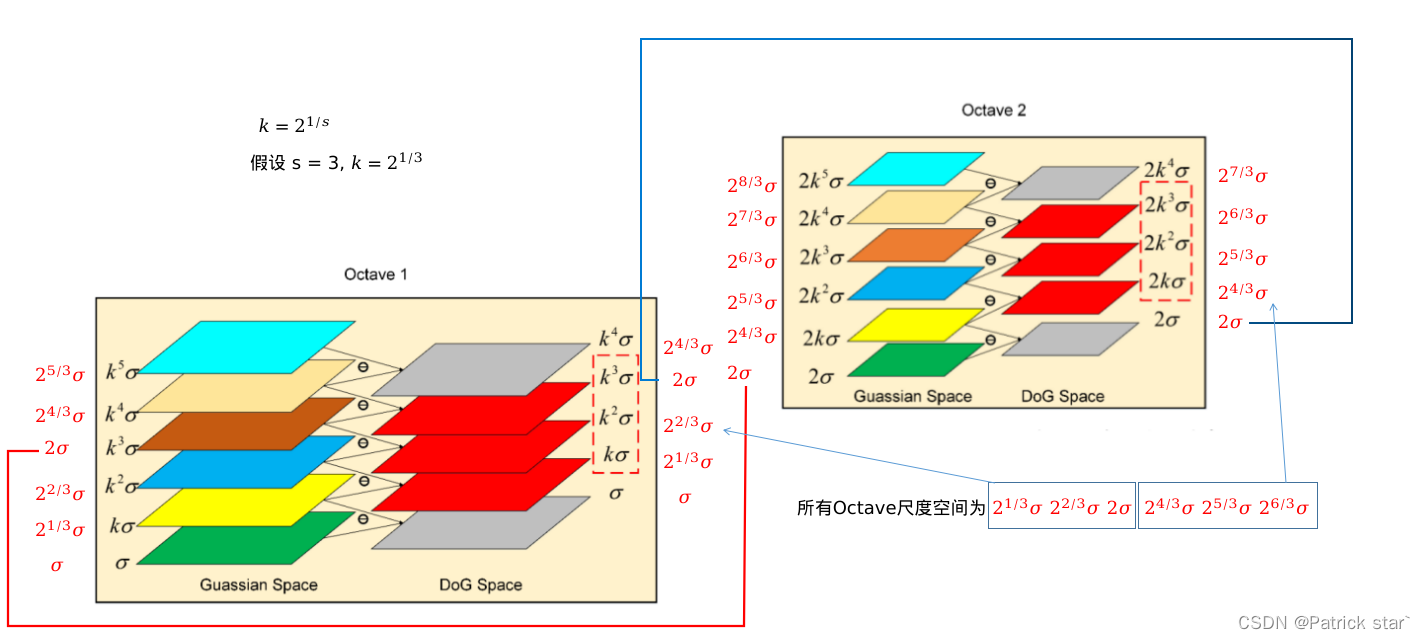
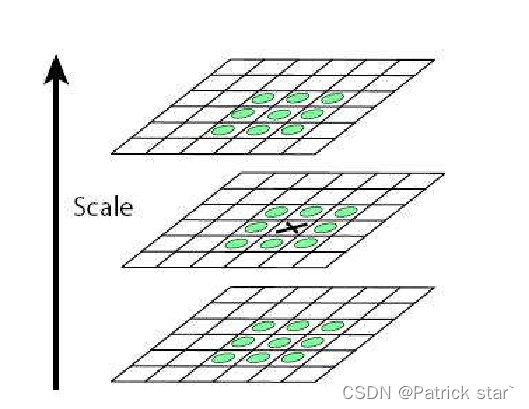
在找合适的尺度空间的时候,会进行非极大值抑制,只有当该点是27(上下两个尺度18个,当前尺度9个)个领接点中的极值时,认为该点为特征点,因此,有效DoG 个数为S时,总共的DoG个数为S+2(首尾不能构成三个尺度空间)。
每一个Octave表示对GuassianSpace缩小1/2后卷积,当我们需要更大的尺度的时候,需要跟大的sigma,意味着更大的卷积核更多的计算。SIFT算法中,将这样操作可以转换为,将图像缩小1/2,得到结果后将响应的sigma放大2倍,这样减少了计算的同时也得到了更大的尺度空间。
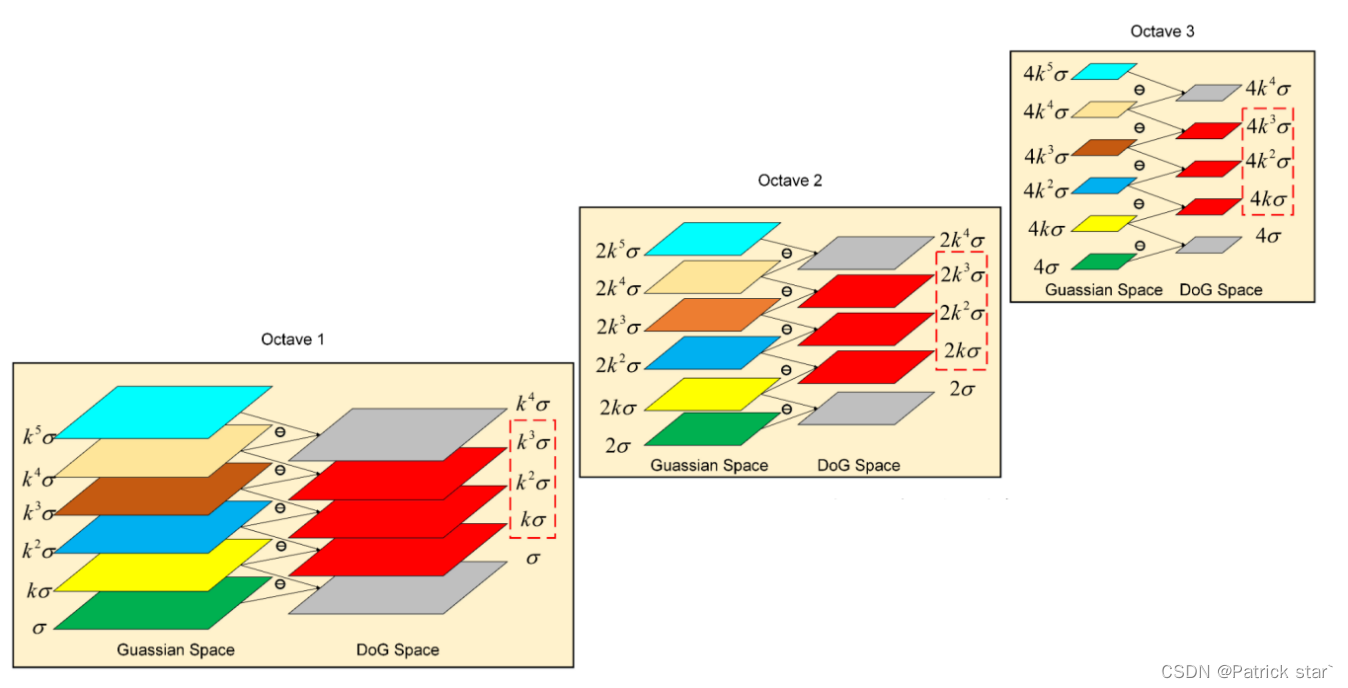
K的取值同样也很讲究,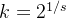 ,s为有效DoG个数。
,s为有效DoG个数。
K这样取值的好处是,对应高斯空间来说,只要将倒数第三图下采样2倍就能得到下一个Octave的第一个图,对于DoG空间来说,当前最后一个有效DoG的sigma与下一个Octave的第一个有效DoG的sigma是连续的(如图所示)