相同的树 单值二叉树 二叉树的最大深度
相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
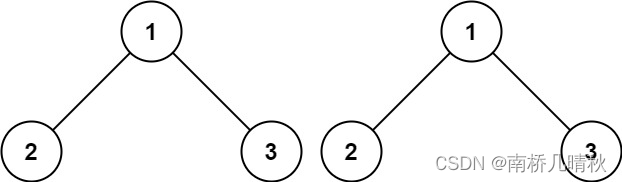
输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:
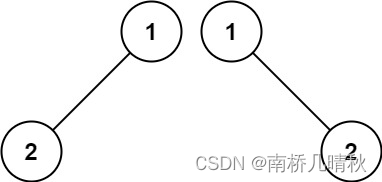
输入:p = [1,2], q = [1,null,2]
输出:false
示例 3:
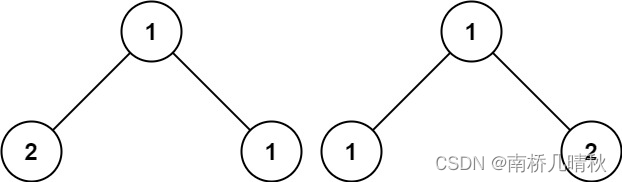
输入:p = [1,2,1], q = [1,1,2]
输出:false
提示:
两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104
分析:
如果两个二叉树都为空,那么这两个二叉树必定相同
如果这两个二叉树一个为空,另一个不为空,那么两个二叉树必定不相等
如果两个二叉树都不为空,那么就判断根节点是否相同:如果不相同,那么两个二叉树必定不相同;如果相同,再去遍历两个二叉树的左子树和右子树。
这是一个递归的过程,也是分治思想,都是去判断两个二叉树自己(根节点)的值是否相同,然后再去遍历左右子树,不是左右孩子。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
单值二叉树
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
示例 1:
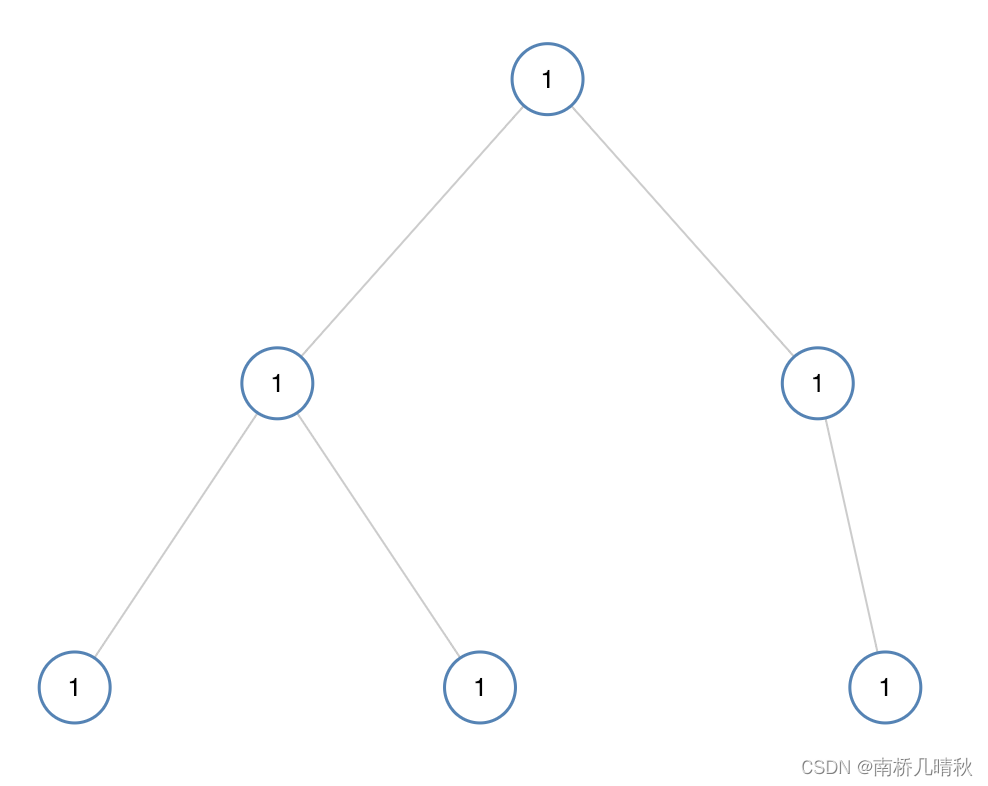
输入:[1,1,1,1,1,null,1]
输出:true
示例 2:
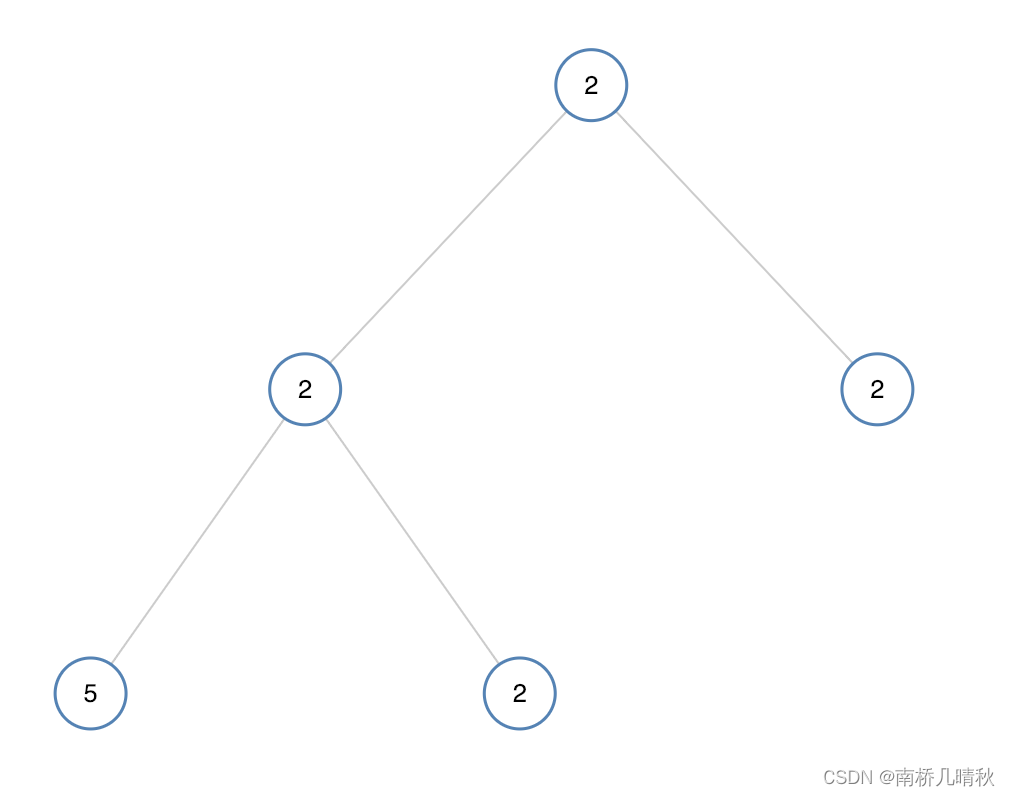
输入:[2,2,2,5,2]
输出:false
提示:
给定树的节点数范围是 [1, 100]。
每个节点的值都是整数,范围为 [0, 99] 。
分析:
单值二叉树,即树上的每个节点的值都是同一个数
检查自己和他的孩子是否相等,如果不相等则返回false;如果相等,则继续遍历左右子树,依然是一个递归过程
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isUnivalTree(struct TreeNode* root) {
if(root==NULL)
return true;
if(root->left&&root->left->val!=root->val)
return false;
if(root->right&&root->right->val!=root->val)
return false;
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}
二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
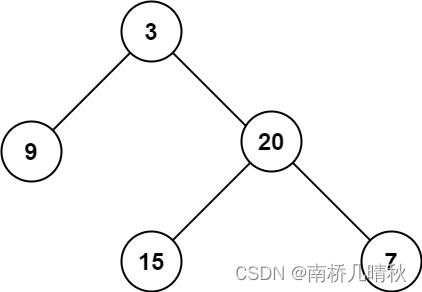
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100
分析:
递归计算出左右子树的最大深度,然后即可算出最大深度
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int maxDepth(struct TreeNode* root) {
if(root==NULL)
return 0;
return fmax(maxDepth(root->left),maxDepth(root->right))+1;
}