数据结构与算法之动态规划算法(DP)

前言

前边我们讲过分治法，分治法的核心是将一个问题分解为n个小问题，最后合并结果。而动态规划算法的核心是穷举法,以及要寻找到一个状态方程，需要用一个DP表或者函数来记录穷举的结果，从穷举过程中选择最优的值，最后得到原始问题的解。

1.0-1背包问题

1.1 基本概念

完全背包问题是背包问题的一种变种，与 0-1 背包问题不同的是，每个物品可以无限次选择放入背包，即可重复使用。动态规划是解决完全背包问题的常用方法。

1.2 具体问题

有n个物品，每个物品的价值为Vi,重量为Wi,背包的容量为C，现在需要将n个物品放入背包，总重量不能超过背包的容量，使得装入的物品的价值达到最大。
求解的问题：放入背包的价值最大
约 束 条 件：重量之和不能超过背包的容量。

实际例子： 假设物品的个数为5个，背包的容量为20，物品的价值和重量如下：

物品编号	1	2	3	4	5
价值v	4	5	10	12	15
重量w	3	4	7	9	12

简单的例子我们可以穷举下：
1.20=4+7+9 此时的价值为: 5+10+12=27
2.19=7+12 此时的价值为：10+15 =25
…等等

1.3 c代码求解

/**
 * 0-1 背包问题
 * @param n 物品的个数
 * @param c 背包的容量
 * @param w 物品的重量数组
 * @param v 物品的价值数组
 * @return dp表
 */
int ** KnapsackDp(int n,int c,int *w,int *v,int ** path){

    int i,tempc;
    //定义一个二维的数组dp表
    int ** dp = (int **)malloc(sizeof (int*)*(n+1));
    for(int i=0;i<=n;i++){
        dp[i]= (int *)malloc(sizeof (int )*(c+1));
    }
    //由于下标是从0开始初始化第一行
    for(tempc = 0;tempc <= c ;tempc ++){
        dp[0][tempc]=0;
        path[0][tempc]=0;
    }
    for(i = 1;i <= n ;i ++){
        dp[i][0]=0;
        path[i][0]=0;
        //开始动态
        for(tempc = 1 ; tempc <= c ; tempc++){
            path[i][tempc]=0;
            if( w[i-1] <= tempc){
                //背包的剩余重量大于物品重量
                if(v[i-1]+dp[i-1][tempc-w[i-1]] > dp[i-1][tempc]){
                    //放入背包
                    dp[i][tempc]=v[i-1]+dp[i-1][tempc-w[i-1]];
                    path[i][tempc]=1;
                }else{
                    dp[i][tempc]=dp[i-1][tempc];
                }
            }else{
                dp[i][tempc]=dp[i-1][tempc];
            }
        }

    }
    return dp;
}

1.4 测试

int main(){

    int n=5;
    int c=20;
    int w[]={3,4,7,9,12};
    int v[]={4,5,10,12,15};
    //记录是否放入
    int ** path = (int **)malloc(sizeof (int*)*(n+1));
    for(int i=0;i<=n;i++){
        path[i]= (int *)malloc(sizeof (int )*(c+1));
    }
    int **dp = KnapsackDp(n,c,w,v,path);
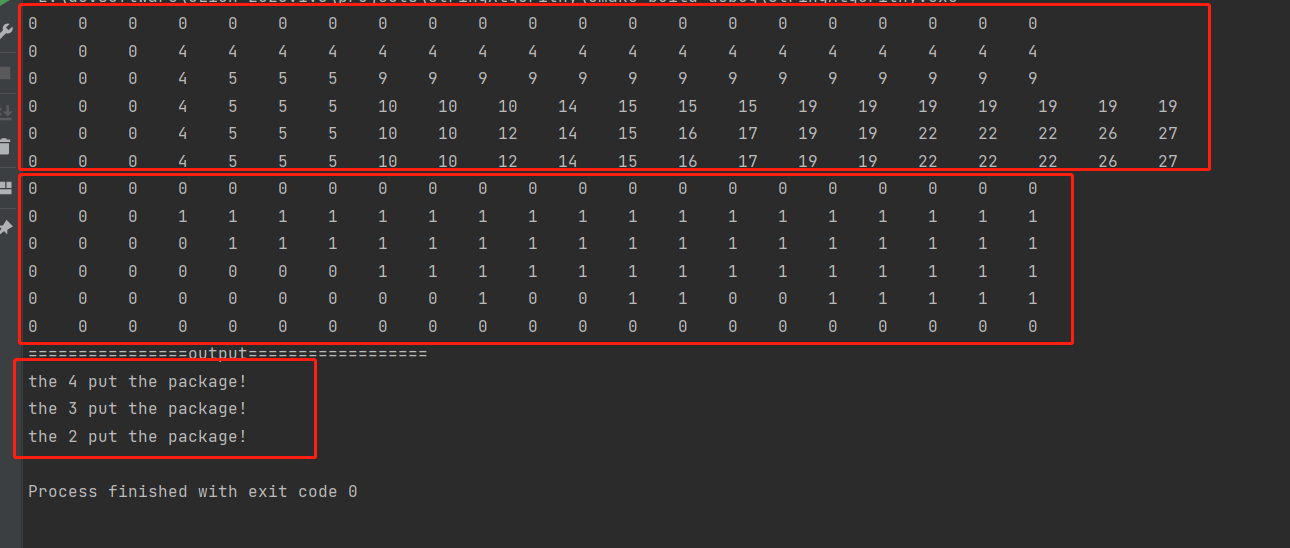
    for (int i = 0; i <=n ; ++i) {
        for (int j = 0; j <= c ; ++j) {
            printf("%d    ",dp[i][j]);
        }
        printf("\n");
    }
    for (int i = 0; i <=n ; ++i) {
        for (int j = 0; j <= c ; ++j) {
            printf("%d    ",path[i][j]);
        }
        printf("\n");
    }
    printf("================output==================\n");
    while ( n >0 && c >0 ){
        if(path[n][c]==1){
           c = c-w[n-1];
            printf("the %d put the package!\n",n);
        }
        n--;

    }
}

2.最长公共子序列

先看一张动态图

代码实现也很简单了