无线通信MIMO的线性等效——NAIC2021无线通信赛道优胜奖方案分享

最近参加NAIC2021的AI+无线通信比赛，发现无线通信的MIMO过程虽然复杂，但其实是可以进行线性等效的，可以完全等效为一个较大规模矩阵的线性变换，也可以近似等效为一个较小规模对角矩阵的线性变换。这次比赛多数选手是利用了神经网络万能逼近的性质来完成求解的，但我是利用这种等效变换来做的，根本没有使用神经网络，而是使用这种方法可以得到了解析解。这种方法在精度和速度上有很高的性能，也非常方便对MIMO过程进行更多深入的分析。由于我不是学通信专业的，只是做这个比赛的一点总结，是否真的对通信有用我也不知道，只是花了时间去钻研它不想浪费，怕时间长忘了，放到这里存档。
赛题链接：https://naic.pcl.ac.cn/contest/10/34/71
由于决赛现场时间紧张我代码没有完全写完，所以仅得优胜奖，但我觉得这个方法应该是很不错的。文章是赛后不久就写好了，但过了一年后才发布。

1 MIMO过程描述

我们知道MIMO是由多个发射天线和接收天线组成的单个传输过程的组合，对于单个发射天线到单个接收天线的传输过程大概可以用下图描述，主要包括信号调制、反傅里叶变换到时域、加CP（循环前缀）、削峰（防止功率超限）、沿多输入多输出的天线阵组成的信道传输、去CP、傅里叶变换到频域、信号解调。

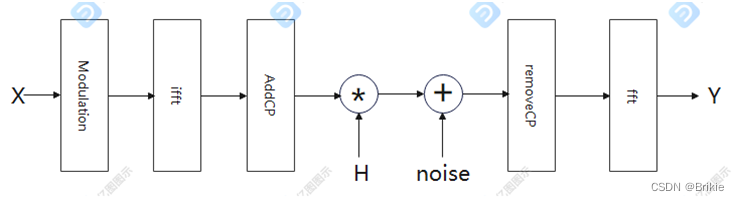
用python代码写出来MIMO过程的模型如下：

import numpy as np

def Modulation(bits):
    '''调制，先把0,1信号变成-0.7071,0.7071；再分虚实部转为复数'''
    bits = (2*bits - 1) * 0.7071
    bits = bits.reshape(-1, 2)
    return bits[:,0] + 1j * bits[:,1]

def addCP(signal, CP):
    '''加入循环前缀'''
    return np.hstack([signal[-CP:], signal])

def removeCP(signal, CP, K):
    '''去掉循环前缀'''
    return signal[CP:CP+K]

def channel(signal, channelResponse, SNRdb):
    '''单个信道的传输过程等于对信道响应卷积，再加上高斯噪声'''
    convolved = np.convolve(signal, channelResponse)
    sigma2 = 0.0015 * 10 ** (-SNRdb / 10)
    noise = np.random.randn(*convolved.shape) + 1j * np.random.randn(*convolved.shape)
    noise = np.sqrt(sigma2 / 2) * noise
    return convolved + noise

def ofdm(beam_forming, channelResponse, SNRdb, CP = 32):
    '''单个信道的OFDM发送-传输-接收过程'''
    OFDM_time = np.fft.ifft(beam_forming)
    signal_T = addCP(OFDM_time, CP)
    signal_R = channel(signal_T, channelResponse, SNRdb)
    OFDM_R_time = removeCP(signal_R, CP, K=beam_forming.shape[0])
    OFDM_R = np.fft.fft(OFDM_R_time)
    return OFDM_R

def MIMO(X, H, SNRdb):
    '''MIMO过程等于各单信道OFDM过程的组合。X是待发送的0,1信号矩阵，H是信道矩阵'''
    T = H.shape[0]
    R = H.shape[1]
    Y=[]
    for i in range(R):
        yi = []
        for j in range(T):
            bf = Modulation(X[j])
            yj = ofdm(bf, H[j,i,:], SNRdb)
            yi.append(yj)
        Y.append(sum(yi))
    Y=np.asarray(Y)
    return Y

2 MIMO的线性等效

  通常，我们需要从MIMO的输出还原出输入信号，也就是要求MIMO的逆过程。这有很多工程上的方法，在这次比赛中多数选手开发了神经网络来实现这个逆过程。而实际上如果我们能够推导一个数学表达式来等效上述代码表示的模型，那我们就有可能使用数学方法得到逆过程的解析形式的数学表达式，使用数学表达式往往可以得到比神经网络更准确或更快的计算性能。

2.1 对 +CP channel -CP过程线性等效

  我们先来个简单的，只对其中的+CP channel -CP这三个步骤等效为线性函数，因为除了这三个步骤之外，其他的过程都是可以有逆计算的，因此只要把这三个步骤等效为可以拟计算的线性函数之后，就可以得到整个过程的逆计算。
  我们令这三个步骤可以等效为$y=Cx+ϵ$，其中$ϵ$表示高斯噪声
其中的C可以用以下代码求解：

'''以32T2R，信道时延delay=126, 子载波数256为例：'''
T,R,delay = 32,2,126
idx = np.array([np.roll(np.arange(256),v) for v in range(256)]).T
idx_ = idx.copy()
idx[idx>=delay] = 0
def calc_c(h):
    '''h:单个信道，c:单个信道的三步骤等效矩阵(256,256)'''
    c = h[idx]
    c[idx_>=delay] = 0
    c[:(delay-cp),256-delay+1:256-cp] = 0
    return c
'''再计算MIMO的等效线性变换矩阵，H是信道矩阵(T,R,delay)'''
C = []  # 线性方程系数矩阵，(Rx256, Tx256)
for i in range(R):
    C_ = []
    for j in range(T):
        h = H[j,i]
        Cij = calc_c(h)
        C_.append(Cij)
    C_ = np.array(C_)
    C.append(C_)
C = np.array(C)

不考虑传输时加入的高斯噪声，我们检验等效变换矩阵是否正确：

x = np.random.binomial(n=1, p=0.5, size=(32,512))
y = MIMO(x, H, SNRdb=10000)#SNRdb=10000表示无噪声

x_qam=[]
for i in range(T):
    x_qam.append(Modulation(x[i]))
x_qam = np.array(x_qam)
x_ = np.fft.ifft(x_qam)
x_ = np.einsum('rtij,tj->ri',C,x_)
y_C = np.fft.fft(x_)

可以随机选择信道矩阵H和输入信号x，可发现y和y_C是相等的。注意其中在计算$y=Cx$时，由于MIMO情形下的C是多维矩阵，我们使用爱因斯坦求和约定法（np.einsum）来计算，更加便捷。

求解其逆运算：

用线性变换替代中间三步骤之后，则可以把整个MIMO表述如下：
$y=fft(C(ifft(x))+ϵ)$
易推出其逆运算为：
$x=fft(C^{+}(ifft(y))-ϵ)$，式中$C^{+}$表示$C$的广义逆矩阵

2.2 对全过程线性等效

fft和ifft可以等效为如下的矩阵乘法
$fft(x)=F\times x$
$ifft(x)=IF\times x$
式中，$I$是单位矩阵，记$F=fft(I)$,$IF=ifft(I)$。
所以整个MIMO过程可以用单个线性矩阵乘法等效：
$y=fft(C(ifft(x))+ϵ)$ 等价于,
$y=F\times C\times IF\times x+{ϵ}_1$
式中，${ϵ}_1=F\times ϵ$也是高斯分布
记$A=F\times C\times IF$，则可得
$y=A\times x+{ϵ}_1$
这样就得到了全过程的线性矩阵乘法等效。我们可以把上面的推导写成代码并检验：

F=np.fft.fft(np.diag(np.ones([256])))
IF=np.fft.ifft(np.diag(np.ones([256])))
A = np.zeros([T,R,256,256],dtype='complex64')
for i in range(T):
    for j in range(R):
        h = H[i,j]
        Cij = calc_c(h)
        A[i,j] = F @ Cij @ IF
y_A = np.einsum('trwv,tv->rw',A,x_qam)

经验证，y_A的值和上面y, y_C的值是一样的。
在不考虑噪声时，很容易求得MIMO过程的逆运算：
$x=A^{+}\times y$ ，式中$A^{+}$表示$A$的（左）广义逆矩阵
我们用代码检验这个逆运算(注意必须R≥T下段才成立，对于T>R时，无法从输出求解输入，或者说此时的A不存在左广义逆)：

A_ = rearrange(A,'r t i j -> (r i) (t j)')
A_pinv = np.linalg.pinv(A_)
x_pre = A_pinv @ y.reshape(-1)
x_pre = rearrange(x_pre,'(t j)-> t j',t=T,j=256)

可以对比逆向求解的x_pre和输入的x_qam，发现它们是相等的。

2.3 对全过程的简化近似线性等效

有了上述等效方程，我们就可以直接用矩阵运算来求解MIMO过程和其逆过程，但是上述等效方程的系数矩阵A是很大的，运算量很大，正向计算时比第1节中提到的代码直接计算还要慢。
仔细观察会发现，每个信道的等效Aij矩阵都是近似对角矩阵（除了对角线元素，其他值都很小，近似对角化的原因是卷积和CP操作造成的，CP越大越近似对角阵）。这样我们只保留Aij的对角线元素，可以给系数矩阵降低一个维度，计算量就大大降低了。我们称近似后的矩阵为$\lambda$，有
$y\approx \lambda \times x+{ϵ}_1$ 式中，$\lambda =diagonal(A)$
用python代码检验如下：

Lam = np.diagonal(A,axis1=2,axis2=3)
y_2 = np.einsum('rti,ti->ri',Lam,x_qam)
plt.plot(y.real[1]);plt.plot(y_2.real[1])

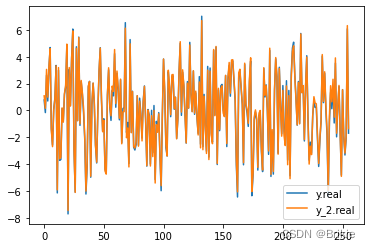
此时的逆运算过程也更为简单：（不考虑噪声）
$x={\lambda }^{+}\times y$ ，式中${\lambda }^{+}$表示$\lambda$的广义逆矩阵
代码实现为：

def pinv(A):
    """计算A的加号广义逆，A.shape:(R,T,wave)"""
    assert len(A.shape) == 3
    if A.shape[0] > A.shape[1]:
        ##计算A的伪拟, A为列满秩时，即T<R
        A_pinv = np.matmul(
                        np.linalg.inv(
                            np.matmul(A.transpose(2,1,0).conj(), A.transpose(2,0,1))),
                        A.transpose(2,1,0).conj())
        #I = A_pinv @ A.transpose(2,0,1)
    else:
        ##计算A的伪拟, A为行满秩时，即T>R
        A_pinv = np.matmul(A.transpose(2,1,0).conj(),
                        np.linalg.inv(
                            np.matmul(A.transpose(2,0,1), A.transpose(2,1,0).conj()))
                        )
        #I = A.transpose(2,0,1) @ A_pinv
    return A_pinv

Lam_pinv = pinv(Lam)
I = Lam_pinv @ Lam.transpose(2,0,1)
x_pre = np.einsum('itr,ri->ti',Lam_pinv,y)

对比逆向求解的x_pre和输入的x_qam，可发现它们接近。

3 利用线性等效方程完成接收机设计

这次比赛任务是接收机的设计，也就是根据信道矩阵和接收数据，求解输入信号。比赛中多数团队是设计了一个神经网络来逼近从输出信号到输入信号的映射，根据最后比赛的结果，如果使用精心调参的transformer网络非常充分训练的话（比如训练超过24小时），确实可以达到非常好的效果。但是我仅仅使用了线性等效的方法，完全没有用到神经网络和任何可学习的方法，直接求解也达到了复赛第三的成绩。这种方法非常简单，计算也非常快速。为了更全面的记录线性等效法的全部思路，下面我逐步深入的介绍线性等效的做法。

3.1 用ZF方法：

ZF（zero-force,迫零）法就是用上面的广义逆矩阵求解的方法，显然，如果不考虑噪声时，使用完全等效A矩阵的广义逆，可以从输出信号中100%还原出输入信号。但是对于含噪信号，则会出现部分还原错误，对于使用近似等效的Lam矩阵的ZF方法，由于同时还存在近似误差，所以还原准确率会更低一些。3.2节中的表1给出了不同噪声情况下，使用A和Lam矩阵时的还原率。

3.2 穷举法：

用对角矩阵Lam矩阵近似等效之后，实际上意味着在输入x和输出y上子载波独立，也就是说每个子载波上R个天线上的接收数据完全由对应子载波上T个发射天线的发送数据决定，这种在子载波之间的解耦大大降低了求解空间。由于电磁波是横波可以承载两个维度的波动，每根发射天线是有两个维度合并成的复数，总共有2T个0,1数组成，这样求解空间就是$2^{2T}$，如果T不是很大时求解空间并不是很大，比如本次比赛T为4，求解空间是256，这完全可以用穷举法求解。具体地，首先求出总共256种发射编码对应的输出接收信号（不含噪），然后对比实际接收信号和哪种信号最接近，就可以发送信号是哪种编码了。这种方法会有非常高的精度。

系数矩阵\SNR(dB)	无噪声	20	10	0
A矩阵	1.0	0.9781	0.8966	0.7241
Lam矩阵	0.9945	0.9778	0.9070	0.7374
穷举法	0.99998	0.99997	0.9974	0.8928

4 利用线性等效方程完成发射-接收一体机设计

如果我们在发射端对信号进行预编码，预编码变换矩阵设计为信道传输线性等效矩阵的逆矩阵，就有可能使接收到的信号和发射信号逼近，就可以方便的检测出发射信号。
题目描述：以32T2R为例，任意给出一组4bit（即4维01信号），256子载波的待发射信号$X$，希望给出一个算法，能够对$X$预编码为$\tilde{X}$，$\tilde{X}$是一个32维复向量，每维256子载波的可发射信号，然后经过无线信道传输后，接收到的信号$Y$是一个2维复向量、256子载波的信号，经过对$Y$的解码，得到发射信号的检测结果$\hat{X}$，要求$\hat{X}$和$X$相比准确度越高越好。
我们可以有多个方案，方案一：先用本文前面的方法计算32T2R的等效线性方程A，在预编码时使用A的右广义逆矩阵$A^{+}$进行线性变换，有以下公式成立：
$Y=A\tilde{X}$ , $\tilde{X}=A^{+}{X}_q$
则：$Y=A{A}^{+}{X}_q=X_q$
其中$X_q$是$X$调制成的2维256子载波复向量，和$X$一一对应。
由于信道传输过程的噪声影响，接收到的$\hat{X}$和$X$仍不能完全一致，试验中在SNR为10dB时，准确率约为0.8162。
由于已经用逆矩阵相乘的方法保证了总的传输矩阵是对角阵，已经保证了子载波独立性，可以直接用穷举法计算，所以此时不再需要用到对角近似矩阵Lam，如果使用Lam反而精度会降低到0.7950。
方案二：
仔细分析发现，准确率较低的主要原因是：信号预编码到32根天线的可发射信号$\tilde{X}$时功率值变的很小，每根天线的功率变为原信号的2/32，导致传输过程中受噪声影响很大，到了接收端$Y$处叠加噪声就非常大了。
因此一个解决方案是，对于$\tilde{X}$的发射功率进行放大$\alpha$倍，即
$Y=A\tilde{X}/\alpha$ , $\tilde{X}=\alpha A^{+}{X}_q$
试验结果：放大2倍时准确率就可以提升到0.9643，放大4倍就可以提升到0.99987，放大6倍直接达到1.0。但此时Y的接收功率也会被放大，是否接收天线可以允许，我对通信机理不是很懂，这个我不知道。
更好的方案是根据信道自适应的决定放大系数，保证对于不同的信道，发射功率和接收功率都刚好在允许最大安全功率线上，这样就可以最好的抵消噪声的影响，此时对于接收信号需要做一个归一化缩放，然后再检测发射信号。
方案三：
更好的方案必须对噪声进行处理，使用神经网络的方法可能有希望，留做下一步研究。