深度学习Q&A之卷积神经网络

---

前言

本文是基于《百面深度学习 算法工程师带你去面试》一书，内容也都来自书中，而我会对其中的内容进行些许过滤，将我认为比较重要实用的内容放到博客里，文本虽然来自书中，不过相关的示例图、图片均为本人原创手绘（均带有本人水印）。 如果有人对博客中的图片和动图感兴趣的可以私聊我要无水印的原件。 本系列面向刚入门深度学习的读者，和有一定基础但没有体系了解过深度学习细节的Deep learner。

---

1 卷积基础知识

问题1 简述卷积的基本操作，并分析其与全连接层的区别 （难度：$★$）

分析与解答：

在卷积神经网络出现之前，最常见的神经网络被称为多层感知机（Multi-Layer Perceptron，MLP）。这种神经网络相邻层的节点是全连接的，也就是输出层的每个节点（或者说神经元）会与输入层的所有节点（神经元）连接。如图（a）所示。与全连接网络不同，卷积神经网络主要是由卷积层构成的，它具有局部连接和权值共享等特性，如图（b）所示。

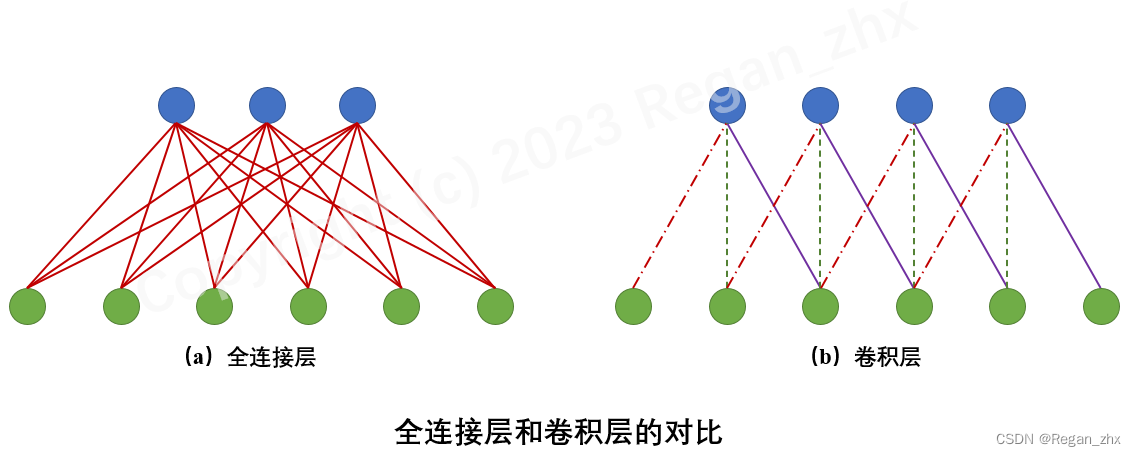
具体来说，卷积层是通过特定数目的卷积核（又称滤波器，filter）对输入的多通道（channel）特征图进行扫描和运算，从而得到多个拥有更高层语义信息的输出特征图（通道数目等于卷积核个数）。Tip：多通道特征图，举个简单例子就是通常的RGB图像可视为三通道的特征图，特征图长和宽与图像像素尺寸一致。

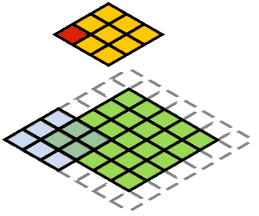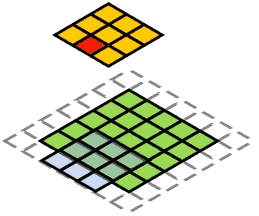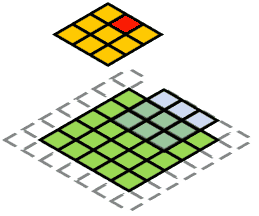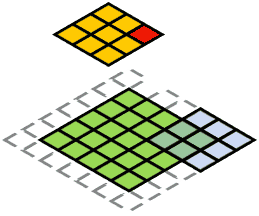
上图形象地描绘了卷积操作的基本过程:下方的绿色方格为输入特征图，蓝色部分是卷积核施加的区域;卷积核不断地扫描整个输入特征图，最终得到输出特征图，也就是上方的橙黄色方格。需要说明的是，输入特征图四周的虚线透明方格，是卷积核在扫描过程中，为了保证输出特征图的尺寸满足特定要求，而对输入特征图进行的边界填充(padding)，一般可以用全零行/列来实现。

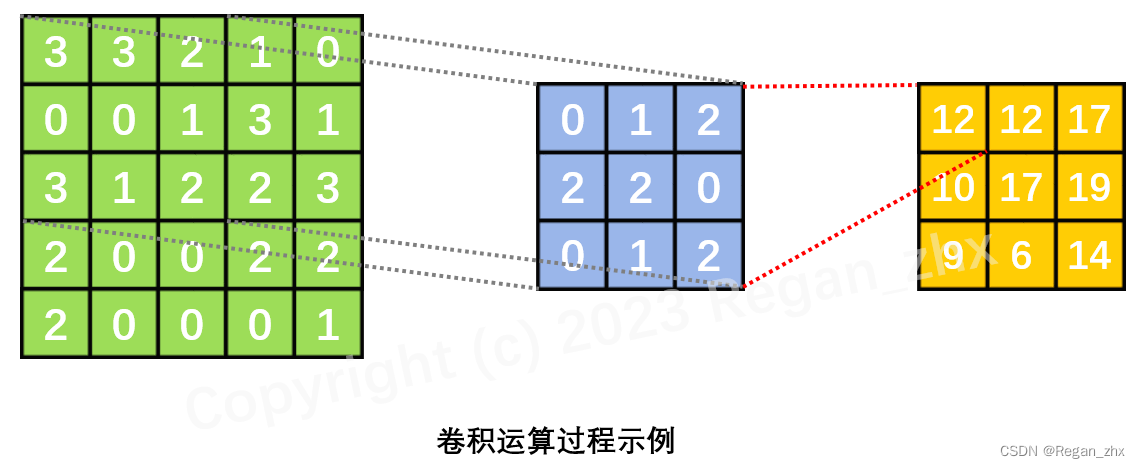
以第一个子图(左上角 )为例，可以看到此时卷积核在输入特征图上的滑动位置即为左上角的 3x3 蓝色阴影区域，输入特征图在该区域对应的取值分别为$\left[\begin{array}{ccc}3& 3& 2\\ 0& 0& 1\\ 3& 1& 2\end{array}\right]$，而卷积核的参数取值为$\left[\begin{array}{ccc}0& 1& 2\\ 2& 2& 0\\ 0& 1& 2\end{array}\right]$，所以输出特征图上对应的棕色方格的取值即为上述两个向量的点积，也即:

$3\times 0+3\times 1+2\times 2+0\times 2+0\times 2+1\times 0+3\times 0+1\times 1-2\times 2=12$。

了解了卷积的基本运算过程之后，我们就能更深刻地理解卷积的特性及其与全连接层的区别。

$♣$ 局部连接:

卷积核尺寸远小于输入特征图的尺寸，输出层上的每个节点都只与输入层的部分节点连接。这个特性与生物视觉信号的传导机制类似，存在一个感受野的概念。与此不同，在全连接层中，节点之间的连接是稠密的，输出层每个节点会与输入层所有节点都存在关联。

$♣$ 权值共享:

卷积核的滑动窗机制，使得输出层上不同位置的节点与输入层的连接权值都是一样的(即卷积核参数)。而在全连接层中，不同节点的连接权值都是不同的。

$♣$ 输入/输出数据的结构化:

局部连接和权值共享，使得卷积操作能够在输出数据中大致保持输入数据的结构信息。例如，输入数据是二维图像(不考虑通道)，采用二维卷积，则输出数据中不同节点仍然保持着与原始图像基本一致的空间对应关系;输入数据是三维的视频(即多个连续的视频帧》，采用三维卷积，则输出数据中也能保持着相应的空间、时间对应关系。若是将结构化信息（如二维图像）输入全连接层，其输出数据会被展成扁平的一维数组，从而丧失输入数据和输出数据在结构上的对应关系。

问题2 在卷积神经网络中，如何计算各层的感受野大小 （难度：$★★$）

分析与解答：

在卷积神经网络中，由于卷积的局部连接性，输出特征图上的每个节点的取值，是由卷积核在输入特征图对应位置的局部区域内进行卷积而得到的，因此这个节点的取值会受到该卷积层的输入特征图，也就是上一层的输出特征图上的某个局部区域内的值的影响，而上一层的输出特征图上的每一点的值亦会受到上上一层某个区域的影响。感受野的定义是，对于某层输出特征图上的某个点，在卷积神经网络的原始输入数据上能影响到这个点的取值的区域。
以二维卷积神经网络为例，如果网络的原始输入特征图的尺寸为$L_w\times L_h$，记网络第 $i$ 层节点的感受野大小为$R_e^{(i)}$，其中 e ∈ { w , h } e \in \{w,h\} e∈{w,h}分别代表宽和高两个方向，则可按照式 Eq.1~Eq.4 来计算。

$\cdot$ 若第 $i$ 层为卷积层或池化层( pooling layer)，则有

$R_e^{(i)}=\min (R_e^{(i-1)}+(k_e^{(i)}-1){\prod }_{j=0}^{i-1}{s}_e^{(j)},L_e)(Eq.1)$

其中，$k_e^{(i)}$是第 $i$ 层卷积核/池化核的尺寸，$s$ 是第层的步长。特别地，对于第0层，即原始输入层，有
$\{\begin{array}{l}{R}_e^{(0)}=1\\ s_e^{(0)}=1(Eq.2)\end{array}$
$\cdot$ 若第 $i$ 层为激活层、批归一化层等，则其步长为1，感受野大小为
$R_e^{(i)}=R_e^{(i-1)}(Eq.3)$
$\cdot$ 若第 $i$ 层为全连接层，则其感受野为整个输入数据全域，即
$R_e^{(i)}=L_e(Eq.4)$
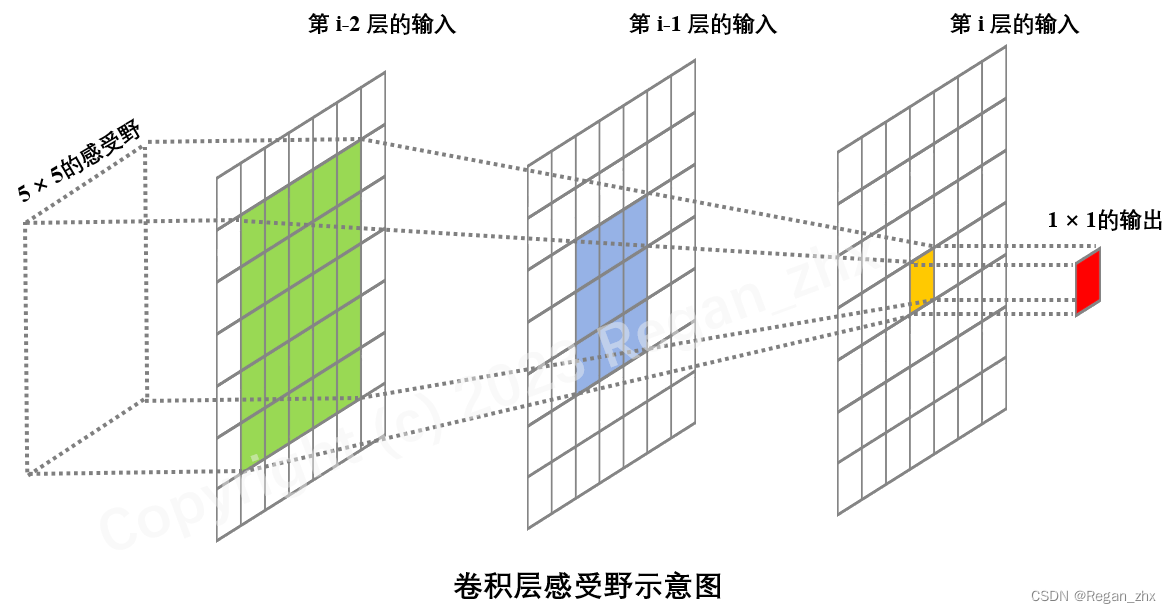
下图为感受野的简单示意图，可以看到，当第 $i-1$ 层和第 $i-2$层的卷积核大小为 $3\times 3$、步长为 1时，使用Eq.1计算可得第 $i$ 层在 $i-1$ 层感受野为$3\times 3$，第 $i$ 层在第 $i-2$ 层上的感受野大小为 $5\times 5$，与图中示例一致。

问题3 卷积层的输出尺寸、参数量和计算量 （难度：$★★$）

假设一个卷积层的输入特征图的尺寸为$l_w^{(i)}\times l_h^{(i)}$，卷积核大小为 $k_w\times k_h$，步长为 $s_w\times s_h$，则输出特征图的尺寸 $l_w^{(o)}\times l_h^{(o)}$ 如何计算? 如果输入特征图的通道数为 $c^{(i)}$，输出特征图的通道数为$c^{(o)}$，在不考虑偏置项(bias)的情况下，卷积层的参数量和计算量是多少?

分析与解答：

$⧫$ 输出尺寸

假设在卷积核的滑动过程中，我们对输入特征图的左右两侧分别进行了 $p_w$ 列填充，上下两侧分别进行了 $p_h$ 行填充，填充后的特征图尺寸为 $(l_w^{(i)}+2p_w)\times (l_h^{(i)}+2p_w)$，则输出特征图的尺寸为
l e ( o ) = l e ( i ) + 2 p e − k e s e + 1 , e ∈ { w , h } l_e^{(o)} = \cfrac{l_e^{(i)} + 2 p_e-k_e}{s_e} + 1, e \in \{ w,h\} le(o)​=se​le(i)​+2pe​−ke​​+1,e∈{w,h}

上述公式在步长 $s_e>1$ 时，可能会出现非整数情况，此时，很多深度学习框架会采取向下 取整的方式，放弃输入特征图的一部分边界数据，使得最终的输出特征图的尺寸为
l e ( o ) = ⌊ l e ( i ) + 2 p e − k e s e ⌋ + 1 , e ∈ { w , h } l_e^{(o)} = \bigg\lfloor\cfrac{l_e^{(i)} + 2 p_e-k_e}{s_e}\bigg\rfloor + 1, e \in \{ w,h\} le(o)​=⌊se​le(i)​+2pe​−ke​​⌋+1,e∈{w,h}

例如，Caffe和PyTorch 会放弃输入特征图的左侧和上侧的一部分数据使得卷积核滑动窗恰好能到达最右下角的点。
有些深度学习框架(如 TensorFlow、Keras)在做卷积运算时无法显式指定输入特征图的边界填充尺寸(当然可以在做卷积之前手动填充)，只能选择以下几种预先定义好的填充模式。
$\cdot$ 若选择 padding-same 模式，则会在输入特征图的左右两侧一共填充 $p_w^{+}=k_w-1$ 列，上下两侧一共填充$p_h^{+}=k_h-1$行，最终的输出特征图的尺寸为
l e ( o ) = ⌊ l e ( i ) − 1 s e ⌋ + 1 , e ∈ { w , h } l_e^{(o)} = \bigg\lfloor\cfrac{l_e^{(i)}-1}{s_e}\bigg\rfloor + 1, e \in \{ w,h\} le(o)​=⌊se​le(i)​−1​⌋+1,e∈{w,h}

例如在 TensorFlow 中，如果$p_e^{+}$为偶数，则在输入特征图的左右两侧或上下两侧填充相等数目的列/行；如果为奇数，会让右侧/下侧比左侧/上侧多填充一列/行。
$\cdot$ 若选择padding=valid模式，则不会对输入特征图进行边界填充而是直接放弃右侧和下侧卷积核无法滑动到的区域，此时输出特征图的尺寸为
l e ( o ) = ⌊ l e ( i ) − k e s e ⌋ + 1 , e ∈ { w , h } l_e^{(o)} = \bigg\lfloor\cfrac{l_e^{(i)}-k_e}{s_e}\bigg\rfloor + 1, e \in \{ w,h\} le(o)​=⌊se​le(i)​−ke​​⌋+1,e∈{w,h}

$⧫$ 参数量

卷积层的参数量，主要取决于每个卷积核的参数量以及卷积核的个数。在这里，每个卷积核含有 $c^{(i)}\times k_w\times k_h$ 个参数，而卷积核的个数即输出征图的通道个数 $c^{(o)}$，因此参数总量为

$c^{(i)}\times c^{(o)}\times k_w\times k_h$

$⧫$ 计算量

卷积层的计算量，由卷积核在每个滑动窗内的计算量以及整体的清动次数决定。在每个滑动窗内，卷积操作的计算量大约为 $c^{(i)}\times k_w\times k_h$，而卷积核的滑动次数即输出特征图的数据个数，也就是$c^{(o)}\times l_w^{(o)}\times l_h^{(o)}$，因此整体的计算量为

$c^{(i)}\times c^{(o)}\times l_w^{(o)}\times l_h^{(o)}\times k_w\times k_h$

一般情况下，有 k e ≪ l e ( i ) , k e ≪ l e ( i ) , e ∈ { w , h } k_e \ll l_e^{(i)}, k_e \ll l_e^{(i)}, e \in \{ w,h\} ke​≪le(i)​,ke​≪le(i)​,e∈{w,h}，因此上式可以近似简写为

$\frac{c^{(i)}\times c^{(o)}\times l_w^{(i)}\times l_h^{(i)}\times k_w\times k_h}{(s_w\times s_h)}$

2 卷积的变种

问题1 简述转置卷积的主要思想以及应用场景（难度：$★★★$）

分析与解答：

普通的卷积操作可以形式化为一个矩阵乘法运算，即
$y=Ax（Eq.5)$

其中，$x$ 和 $y$ 分别是卷积的输入和输出(展平成一维向量形式)，维度分别为 $d^{(i)}$和 $d^{(o)}$；$A$ 是由卷积核、滑动步长决定的常对角矩阵，维度为 $d^{(o)}\times d^{(i)}$，其每一行对应着卷积核的一次滑动位置。以一维卷积为例，假设输入向量 $x=[a,b,c,d,e,f,g{]}^T$，卷积核为 $K=[x,y,z]$，卷积的滑动步长为 2，则输出向量为
$y=x\ast K=\left[\begin{array}{c}ax+by+cz\\ cx+dy+ez\\ ex+fy+gz\end{array}\right]=\left[\begin{array}{ccccccc}x& y& z& 0& 0& 0& 0\\ 0& 0& x& y& z& 0& 0\\ 0& 0& 0& 0& x& y& z\end{array}\right]\left[\begin{array}{c}a\\ b\\ c\\ d\\ e\\ f\\ g\end{array}\right]\triangleq Ax(Eq.6)$

反过来，记 $A^T$ 为矩阵 $A$ 的转置，定义如下矩阵运算
$\hat{y}=A^T\hat{x}(Eq.7)$

其所对应的操作被称为转置卷积，$\hat{x}$ 和 $\hat{y}$ 分别是转置卷积的输入和输出，维度分别为 $d^{(o)}\times d^{(i)}$ 。转置卷积也被称为反卷积( deconvolution )，它可以看作是普通卷积的一个“对称”操作，这种“对称性”体现在以下两个方面。
$\cdot$ 转置卷积能将普通卷积中输入到输出的尺寸变换逆反过来。例如，Eq.5 中的普通卷积将特征图尺寸由 $d^{(i)}$ 变为$d^{(o)}$，而 Eq.7 中的转置卷积则可以将特征图尺寸由 $d^{(o)}$ 复原为 $d^{(i)}$ 。这里需要注意的是，输入特征图经过普通卷积操作后再经过转置卷积，只是复原了形状，并不能复原具体的取值(因此将转置卷积称为反卷积并不是很合适)。Tips：在我看过的比较权威的书籍是说转置卷积和反卷积其实不是同个东西，反卷积在数学里有特定意义，所以还是应该称其为转置卷积为好，请大家忘记反卷积这个词。
$\cdot$ 根据矩阵运算的求导知识，在 Eq.5 所示的普通卷积中，输出 $y$ 对于输入$x$的导数为 $\partial y/\partial x=A^T$ ；而在 Eq.7 所示的转置卷积中，输出 $\hat{y}$ 对于输入 $\hat{x}$ 的导数为 $\partial \hat{y}/\partial \hat{x}=A$ 。由此可以看出，转置卷积的信息正向传播与普通卷积的误差反向传播所用的矩阵相同，反之亦然。

以 Eq.7 为例，我们可以写出转置卷积的具体计算公式:
$y=A^T\ast \hat{x}=\left[\begin{array}{ccc}x& 0& 0\\ y& 0& 0\\ z& x& 0\\ 0& y& 0\\ 0& z& x\\ 0& 0& y\\ 0& 0& z\end{array}\right]\left[\begin{array}{c}\hat{a}\\ \hat{b}\\ \hat{c}\end{array}\right]=\left[\begin{array}{ccccccccc}z& y& x& 0& 0& 0& 0& 0& 0\\ 0& z& y& x& 0& 0& 0& 0& 0\\ 0& 0& z& y& x& 0& 0& 0& 0\\ 0& 0& 0& z& y& x& 0& 0& 0\\ 0& 0& 0& 0& z& y& x& 0& 0\\ 0& 0& 0& 0& 0& z& y& x& 0\\ 0& 0& 0& 0& 0& 0& z& y& x\end{array}\right]\left[\begin{array}{c}0\\ 0\\ \hat{a}\\ 0\\ \hat{b}\\ 0\\ \hat{c}\\ 0\\ 0\end{array}\right](Eq.8)$

可以看到，等号的右侧实际上就是一个普通卷积对应的矩阵乘法。因此，转置卷积本质上就是一个对输入数据进行适当变换(补零/上采样) 的普通卷积操作。在具体实现时，以二维卷积为例，一个卷积核尺寸为 $k_w\times k_h$、滑动步长为 ($s_w,s_h$)、边界填充尺寸为 ($p_w,p_h$) 的普通卷积，其所对应的转置卷积可以按如下步骤来进行。
(1) 对输入特征图进行扩张(上采样): 相邻的数据点之间，在水平方向上填充 $s_w-1$ 个零，在垂直方向上填充 $s_h-1$个零。
(2) 对输入特征图进行边界填充: 左右两侧分别填充 ${\hat{p}}_w=k_w-p_w-1$ 个零列，上下两侧分别填充 ${\hat{p}}_h=k_h-p_h-1$个零行。
(3) 在变换后的输入特征图上做卷积核大小为 $k_w\times k_h$、滑动步长为 (1,1) 的普通卷积操作。

在上述步骤(2)中，转置卷积的边界填充尺寸(${\hat{p}}_w,{\hat{p}}_h$) 是根据与之对应的普通卷积的边界填充尺寸 ($p_w,p_h$) 来确定的，很多深度学习框架 (如PyTorch) 就是按照这个思路来设定转置卷积的边界填充尺寸，但在有些计算框架(如TensorFlow)中，做卷积时无法显式指定边界填充尺寸，只能选择一些预定义的填充模式(如padding=same或padding=valid)，此时，转置卷积的边界填充尺寸是根据与之对应的普通卷积的边界填充模式来设定的 (见1节的问题3) 。
需要注意的是，当滑动步长大于1时，卷积的输出尺寸公式中含有向下取整操作(参见1 节的问题3)，故而普通卷积层的输入尺寸与输出尺寸是多对一关系，此时转置卷积无法完全恢复之前普通卷积的输入尺寸，需要通过一个额外的参数来直接或间接地指定之前的输入尺寸(如TensorFlow中的output_shape 参数、PyTorch中的output_padding参数)。

普通卷积和转置卷积所处理的基本任务是不同的。前者主要用来做特征提取，倾向于压缩特征图尺寸；后者主要用于对特征图进行扩张或上采样，代表性的应用场景如下。
$\cdot$ 语义分割/实例分割等任务: 由于需要提取输入图像的高层语义信息，网络的特征图尺寸一般会先缩小，进行聚合;此外，这类任务一般需要输出与原始图像大小一致的像素级分割结果，因而需要扩张前面得到的具有较高语义信息的特征图，这就用到了转置卷积。
$\cdot$ 一些物体检测、关键点检测任务，需要输出与源图像大小一致的热图。
$\cdot$ 图像的自编码器、变分自编码器、生成式对抗网络等。

问题2 简述空洞卷积的设计思路（难度：$★★$）

分析与解答：

上一问中提到，在语义分割 (Semantic Segmentation) 任务中，一般需要先缩小特征图尺寸，做信息聚合；然后再复原到之前的尺寸，最终返回与原始图像尺寸相同的分割结果图。常见的语义分割模型，如全卷积网络(Fully Convolutional Networks,FCN)，一般采用池化操作(pooling)来扩大特征图的感受野，但这同时会降低特征图的分辨率，丢失一些信息(如内部数据结构、空间层级信息等 )，导致后续的上采样操作(如转置卷积)无法还原一些细节，从而限制最终分割精度的提升。

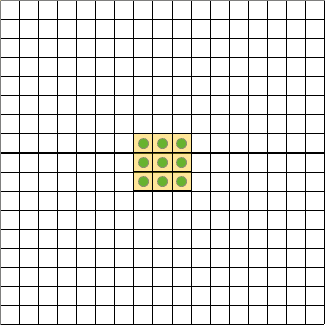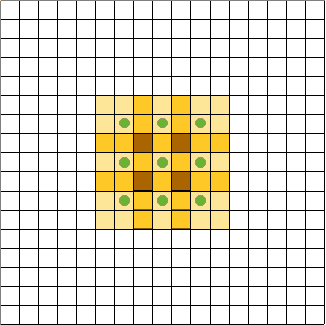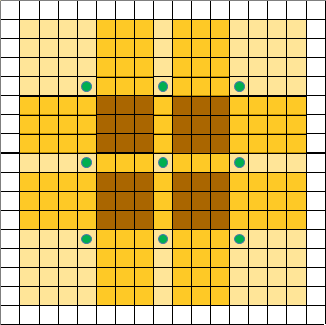
如何不通过池化等下采样操作就能扩大感受野呢? 空洞卷积（Dilated convolution应运而生。顾名思义，空洞卷积就是在标准的卷积核中注入“空洞”，以增加卷积核的感受野。空洞卷积引入了扩张率 (dilation rate )这个超参数来指定相邻采样点之间的间隔: 扩张率为 $r$ 的空洞卷积，卷积核上相邻数据点之间有 $r-1$ 个空洞，如下图所示(图中有绿点的方格表示有效的采样点，黄色方格为空洞)。尺寸为 $k_w\times k_h$ 的标准卷积核，其所对应扩张率为r的空洞卷积核尺寸为 k e + ( r − 1 ) ( k e − 1 ) , e ∈ { w , h } k_e+(r-1)(k_e-1),e\in \{w,h\} ke​+(r−1)(ke​−1),e∈{w,h} 。特别地,扩张率为1的空洞卷积实际上就是普通卷积(没有空洞)。

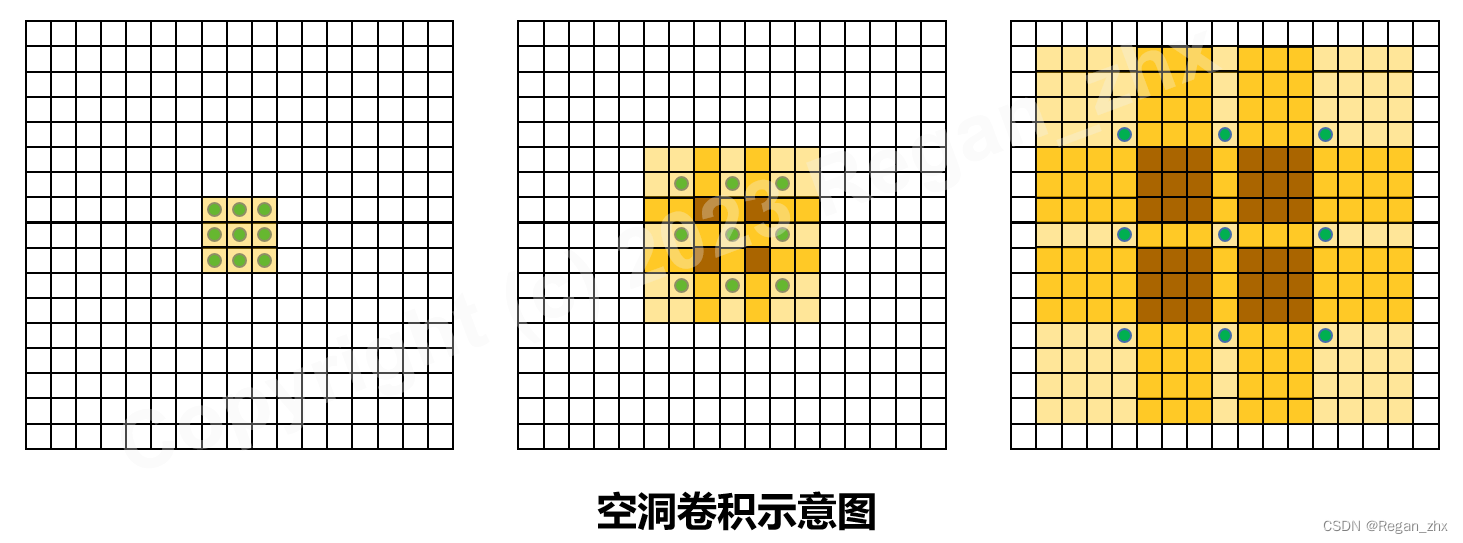
空洞卷积感受野的计算，与上一节中介绍的普通卷积感受野的计算方式基本一致，只是将其中的卷积核尺寸替换为扩张后的卷积核尺( 即包括空洞在内)。以上图为例，假设依次用图 ( a )、( b )、( c ) 中的空洞卷积来搭建三层神经网络:
$\cdot$ 第一层是图 ( a ) 中 $r=1$ 的空洞卷积，扩张后的卷积核尺寸为 $3\times 3$；
$\cdot$ 第二层是图 ( b ) 中 $r=2$ 的空洞卷积，扩张后的卷积核尺寸为 $5\times 5$;
$\cdot$ 第三层是图 ( c ) 中 $r=4$ 的空洞卷积，扩张后的卷积核尺寸为 $9\times 9$。

根据上一节中介绍感受野计算公式，可以算得第一层、第二层、第三层的感受野依次为$3\times 3$、$7\times 7$、$15\times 15$ (如图中黄色阴影部分所示)。如果采用普通的 $3\times 3$ 卷积核，则三层连接起来的感受野只有 $7\times 7$。由此可以看出，空洞卷积利用空洞结构扩大了卷积核尺寸，不经过下采样操作即可增大感受野，同时还能保留输入数据的内部结构。

3 卷积神经网络的基础模块

问题1 批归一化是为了解决什么问题？它的参数有何意义？它在网络中一般放在什么位置？（难度：$★★★$）

分析与解答：

在机器学习中，一般会假设模型的输入数据的分布是稳定的。如果这个假设不成立，即模型输入数据的分布发生变化，则称为协变量偏移(covariate shift)。模型的训练集和测试集的分布不一致，或者模型在训练过程中输入数据的分布发生变化，这些都属于协变量偏移现象同样，对于一个复杂的机器学习系统，在训练过程中一般也会要求系统里的各个子模块的输入分布是稳定的，如果不满足，则称为内部协变量偏移(internal covariate shift)。对于深度神经网络，其在训练过程中，每一层的参数都会随之更新。以第 $i$ 层为例，其输入数据与之前所有层(第1层到第 $i-1$层) 的网络参数取值都有很大关系:在训练过程中，如果之前层的参数被更新后，第i层的输入数据的分布必然也跟着发生变化，此即为内部协变量偏移。网络越深，这种现象越明显内部协变量偏移会给深度神经网络的训练过程带来诸多问题:
$\cdot$ 网络每一层需要不断适应输入数据的分布的变化，这会影响学习效率，并使学习过程变得不稳定。
$\cdot$ 网络前几层参数的更新，很可能使得后几层的输入数据变得过大或者过小，从而掉进激活函数的饱和区，导致学习过程过早停止。
$\cdot$ 为了尽量降低内部协变量偏移带来的影响，网络参数的更新需要更加谨慎，在实际应用中一般会采用较小的学习率(避免参数更新过快)，而这会降低收敛速度。

在之前的网络训练过程中，一般会采用非饱和型激活函数(如ReLU)、精细的网络参数初始化、保守的学习率等方法来降低内部协变量偏移带来的影响。这些方法会使网络的学习速度太慢，并且最终效果也特别依赖于网络的初始化。

批归一化(Batch Normalization, BN) 就是为了解决上述问题而提出的，它的主要作用是确保网络中的各层，即使参数发生了变化，其输入/输出数据的分布也不能产生较大变化，从而避免发生内部协变量偏移现象。采用批归一化后深度神经网络的训练过程更加稳定，对初始值不再那么敏感，可以采用较大的学习率来加速收敛。
批归一化可以看作带参数的标准化，具体公式为

$y^{(k)}={\gamma }^{(k)}\frac{x^{(k)}-{\mu }^{(k)}}{\sqrt{({\sigma }^{(k)}{)}^2+\epsilon }}+{\beta }^{(k)}$

其中，$x^{(k)}$ 和 $y^{(k)}$ 分别是原始输入数据和批归一化后的输出数据，${\mu }^{(k)}$ 和 ${\sigma }^{(k)}$ 下分别是输入数据的均值和标准差(在 mini-batch上)，$\beta$ 和 ${\gamma }^{(k)}$ 下分别是可学习的平移参数和缩放参数，上标 $k$ 表示数据的第 $k$ 维(批归一化在数据各个维度上是独立进行的)，$\epsilon$ 是为防止分母为0的一个小量。
可以看到，在批归一化过程中，设置了两个可学习的参数 $\beta$ 和 $\gamma$ 它们有如下作用:
$\cdot$ 保留网络各层在训练过程中的学习成果。如果没有 $\beta$ 和 $\gamma$，批归一化退化为普通的标准化，这样在训练过程中，网络各层的参数虽然在更新，但是它们的输出分布却几乎不变( 始终是均值为 0、标准差为1)，不能有效地进行学习。添加 $\beta$ 和 $\gamma$ 参数后，网络可以为每个神经元自适应地学习一个量身定制的分布(均值为$\beta$、标准差为 $\gamma$)，保留每个神经元的学习成果。
$\cdot$保证激活单元的非线性表达能力。上面提到，没有 $\beta$ 和 $\gamma$，批归一化的输出分布始终是均值为 0、标准差为 1。此时，如果激活函数采用诸如Sigmoid、Tanh 等函数，则经过批归一化的数据基本上都落在这些激活函数的近似线性区域，没能利用上它们的非线性区域，这会极大地削弱模型的非线性特征提取能力和整体的表达能力。添加 $\beta$ 和 $\gamma$ 参数后，批归一化的数据就可以进入激活函数的非线性区域。
$\cdot$使批归一化模块具有自我关闭能力。若 $\beta$ 和 $\gamma$ 分别取数据的均值和标准差，则可以复原初始的输入值，即关闭批归一化模块。因此，当批归一化导致特征分布被破坏，或者使网络泛化能力减弱时，可以通过这两个参数将其关闭。

至于批归一化在网络中的位置，直觉上看无论是放在激活层之前还是之后都有一定道理。
$\cdot$ 把批归一化放在激活层之前，可以有效避免批归一化破坏非线性特征的分布;另外，批归一化还可以使数据点尽量不落入激活函数的饱和区域，缓解梯度消失问题。
$\cdot$ 由于现在常用的激活函数是 ReLU，它没有 Sigmoid、Tanh座数的那些问题，因此也可以把批归一化放在激活层之后，避免数据在激活层之前被转化成相似的模式从而使得非线性特征分布趋于同化。

在具体实践中，原始论文是将批归一化放在激活层之前的，但学术界和工业界也有不少人曾表示倾向于将批归一化放在激活层之后(如论文共同作者Christian Szegedy、Keras 作者 FrancoisCholle、知名数据科学平台 Kaggle的前首席科学家 Jeremy Howard等人)。从近两年的论文来看，有一大部分是将批归一化放在激活层之后的，如MobileNet v2、ShuffleNet v2、NASNet-A。批归一化究竟应该放在什么位置，仍是一个存争议的问题。

问题2 卷积神经网络中的瓶颈结果和沙漏结构提出的初衷是什么？可以应用于哪些问题？（难度：$★★★★$）

$♠$ 瓶颈结构

瓶颈结构是在GoogLeNet/Inception-v1中提出的，而后的ResNet、MobileNet 等很多网络也采用并发展了这个结构，瓶颈结构的初衷是为了降低大卷积层的计算量，即在计算比较大的卷积层之前先用一个 $1\times 1$ 卷积来压缩大卷积层输入特征图的通道数目，以减小计算量;在大卷积层完成计算之后，根据实际需要，有时候会再次使用一个 $1\times 1$ 卷积来将大卷积层输出特征图的通道数目复原。由此，瓶颈结构一般是一个小通道数的 $1\times 1$ 卷积层，接一个较大卷积层，后面可能还会再跟一个大通道数的 $1\times 1$ 卷积层( 可选)，如图所示

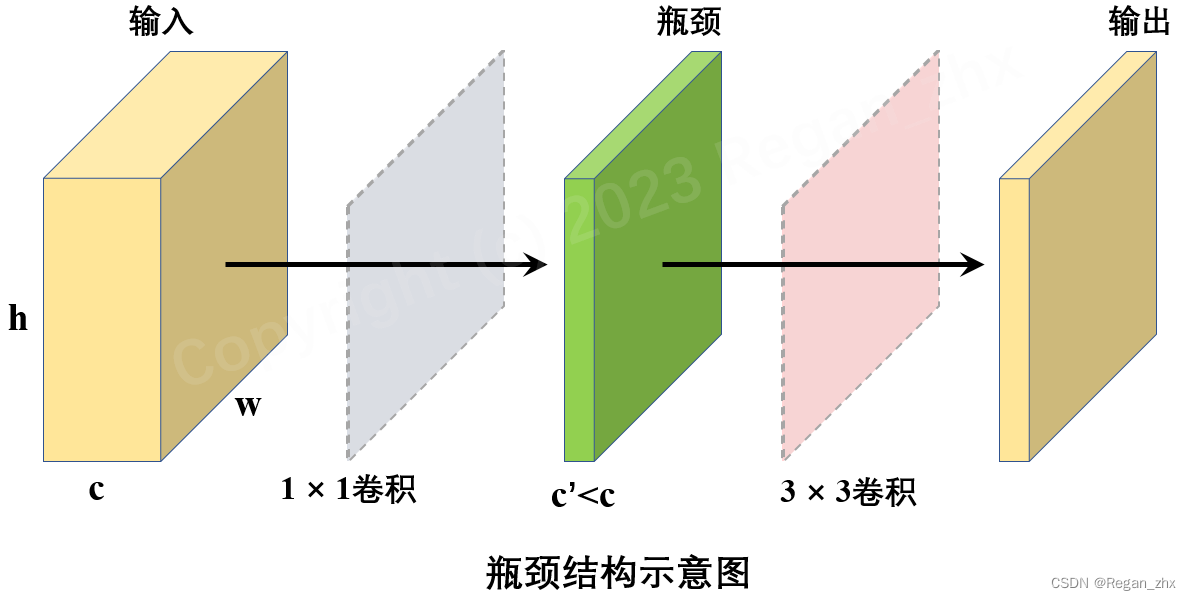
瓶颈结构是卷积神经网络中比较基础的模块，它可以用更小的计算代价达到与之前相似甚至更好的效果(因为瓶颈结构会增加网络层数，所以特征提取能力可能也会有相应提升)。瓶颈结构基本上可以用于所有的卷积神经网络中，场景包括物体检测和分割、生成式对抗网络等大方向，以及诸如人脸匹配、再识别、关键点检测等细分领域。

$♠$ 沙漏结构

沙漏结构也是卷积神经网络中比较基础的模块，它类似于瓶颈结构但尺度要更大，涉及的层也更多。沙漏结构一般包括以下两个分：
(1) 自底向上(bottom-up)分支: 利用卷积、池化等操作将特征图的尺寸逐层压缩(通道数可能增加)，类似于自编码器中的编码器encoder)
(2)自顶向下(top-down)分支:利用反卷积或插值等上采样操作将特征图的尺寸逐层扩大(通道数可能降低)，类似于自编码器中的解码器(decoder)

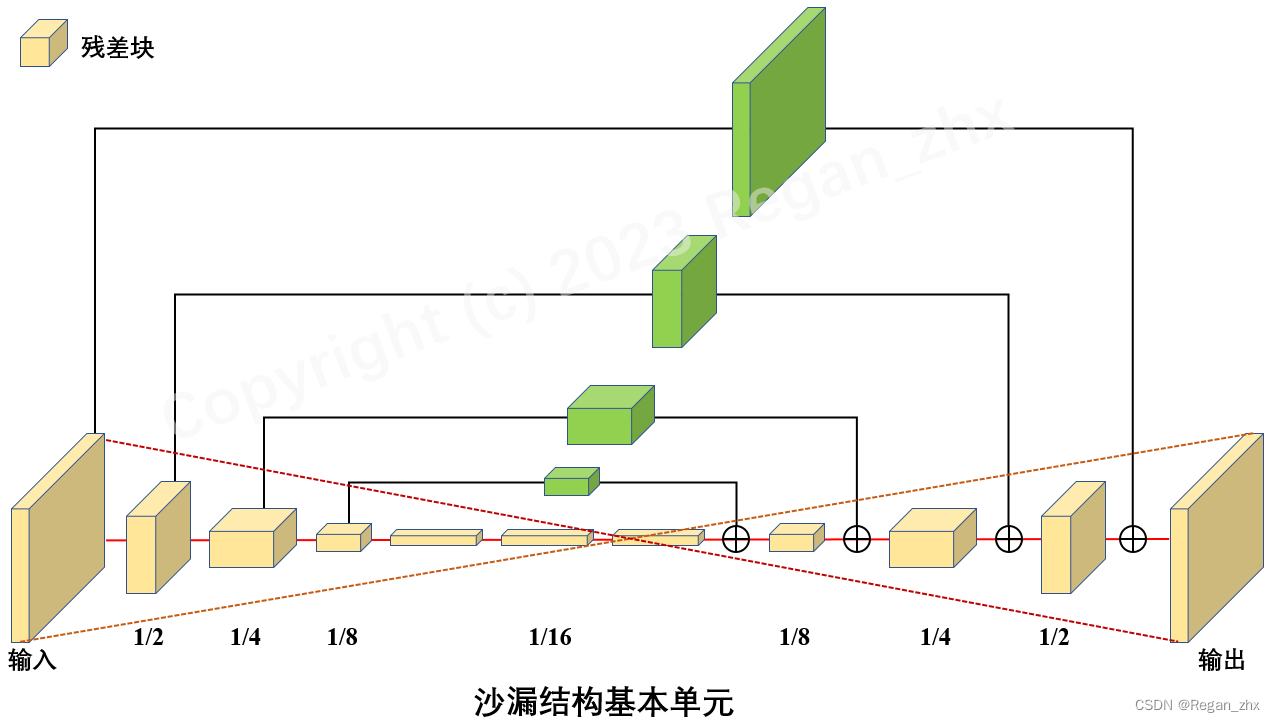
在“ECCV2016 Stacked hourglass networks for human pose estimation”一文中用具有沙漏结构的网络来解决人体姿态估计任务，其基本单元如上图所示，整个网络则由多个沙漏结构堆叠而成。此外，在物体检测任务中，沙漏结构也有着大量应用，如TDM ( Top-Down Modulation )、FPN (Feature PyramidNetwork )、RON ( Reverse connection with Objectness priorNetworks ) 、DSSD ( Deconvolutional Single-Shot Detector )、RefineDet等模型。