R语言数据降维——主成分分析
R语言数据降维——主成分分析
一、项目环境
- 开发工具:RStudio
- R:3.5.2
- 相关包:sqldf,dplyr
二、导入数据
# 这里我们使用的是鸢尾花数据集(iris)
data(iris)
head(iris)
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species | |
|---|---|---|---|---|---|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| 6 | 5.4 | 3.9 | 1.7 | 0.4 | setosa |
相关数据解释:
-
Sepal.Length:萼片长度
-
Sepal.Width:萼片宽度
-
Petal.Length:花瓣长度
-
Petal.Width:花瓣宽度
-
Species:鸢尾花品种
三、 数据划分
library(dplyr)
library(sqldf)
# 为数据集增加序号列(id)
iris$id <- c(1:nrow(iris))
# 将鸢尾花数据集中70%的数据划分为训练集
iris_train <- sample_frac(iris, 0.7, replace = TRUE)
# 使用sql语句将剩下的30%花费为测试集
iris_test <- sqldf("
select *
from iris
where id not in (
select id
from iris_train
)
")
# 去除序号列(id)
iris_train <- iris_train[,-6]
iris_test <- iris_test[,-6]
【注】:这里使用到sqldf包的函数sqldf函数来时间在R语言中使用SQL语句
四、 进行主成分分析
# 对鸢尾花数据集的前4列进行主成分分析
iris_train_pca <- princomp(iris_train[,1:4])
# 绘制碎石图
screeplot(iris_train_pca, npcs = ncol(iris_train),type="lines")
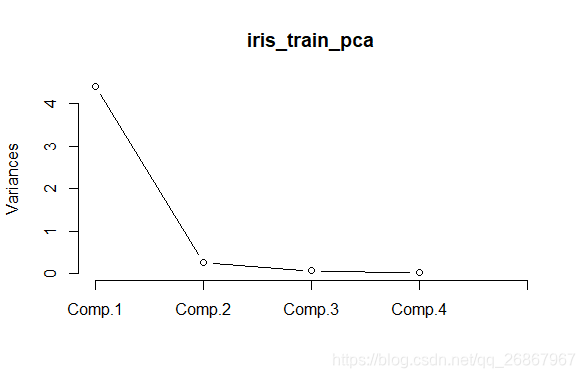
【注】:碎石图的分析方法主要是根据纵坐标的值,纵坐标值越大就表示表示该主成分能够解释的方差的比例越大,因此一般情况下我们会选择纵坐标值较大的几个主成分。
五、 提取主成分的信息
# 第一行是特征值(Standard deviation),
# 第二列是方差的贡献率(Proportion of Variance)
# 第三列是累计方差的贡献率(Cumulative Proportion)
# 方差的贡献率: 标准化后的特征值,全部相加等于100%
# 累计方差的贡献率:累加后的方差的贡献率
summary(iris_train_pca)

【注】:特征值越大,它所对应的主成分变量包含的信息就越多
从输出的结果我们可以得知,在输出的4个主成分中,前两个主成分就包含了原来4个指标98.20%的信息,也就是能够解释98.20%的方差。因此,将前两个作为鸢尾花数据集的主成分。
六、 查看各个主成分与原始数据的关系
# loadings代表每一个成分中之前特征系数
iris_train_pca$loadings
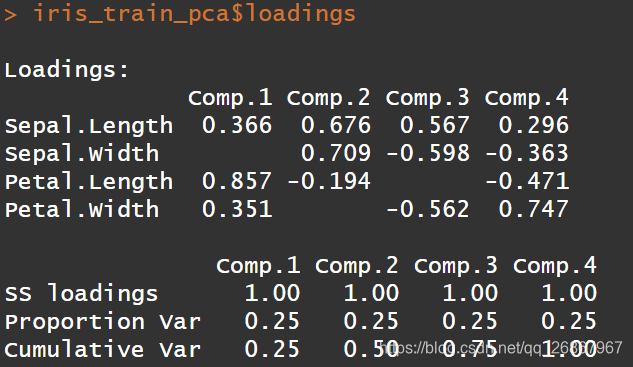
loadings显示的是载荷的内容,这个值实际上是主成分对于原始变量Sepal.Length,Sepal.Width ,Petal.Length ,Petal.Width的系数。也是特征值对应的特征向量,它们是线性无关的单位向量。第1列表示主成分一的得分系数,依次类推。据此可以写出由标准化变量所表达的主成分的关系式,即:
C
o
m
p
.
1
=
0.366
×
S
e
p
a
l
.
L
e
n
g
t
h
+
0.857
×
P
e
t
a
l
.
L
e
n
g
t
h
+
0.351
×
P
e
t
a
l
.
W
i
d
t
h
Comp.1 = 0.366 × Sepal.Length + 0.857 × Petal.Length + 0.351 × Petal.Width
Comp.1=0.366×Sepal.Length+0.857×Petal.Length+0.351×Petal.Width
C
o
m
p
.
2
=
0.676
×
S
e
p
a
l
.
L
e
n
g
t
h
+
0.709
×
S
e
p
a
l
.
W
i
d
t
h
−
0.194
×
P
e
t
a
l
.
L
e
n
g
t
h
Comp.2 = 0.676 × Sepal.Length + 0.709 × Sepal.Width - 0.194 × Petal.Length
Comp.2=0.676×Sepal.Length+0.709×Sepal.Width−0.194×Petal.Length
七、 对测试集进行降维处理
# 使用之间建好的公式对测试集进行降维处理
# new_test <- as.matrix(iris_test[,1:4])%*%as.matrix(iris_train_pca$loadings[,1:2])
# 用上面这种方法进行计算可能会出现问题,建议使用下面这种
new_test <- predict(iris_train_pca, iris_test[,-5])
# 转化为数据框
new_test <- as.data.frame(new_test)
【注】:iris_train_pca$loadings[,1:2] 之所以这里取前两个数是因为之前主成分分析确定的。
这样就达到了对数据进行降维的作用,同时可以将降维后的数据用与机器学习以降低维度过多,而造成的计算时间过长等问题。
需要注意的是,这里的训练集和测试集维度必须完全相同,也就是说如果之前有与预先对训练集进行其他影响维度的操作,那么后续也需要对测试集进行相应的操作,才能保证降维的成功
很长一段时间没有在csdn中写文章了,事实上后面自己学习过程中的大部分文档都是在语雀中完成的,基本都是自己写自己看。后续文章都会分享到自己的个人博客上,感兴趣的话可以关注一下。个人博客地址