第一单元用python学习微积分（二）导数（上）- 瞬时速度 -- vscode -- pygame

二、课程内容，导数可以在几何中表示曲线的变化率，同时也可以在物理中表现速度的变化率

三、python的展示，找找资料，选定了用pygame来展示这个南瓜坠落的实验。

一、准备：

安装vs code https://code.visualstudio.com/Download

安装pygame

pip install pygame

如果你的系统路径的python不是anaconda，还需要把sympy安装下

pip install sympy

二、课程内容，导数可以在几何中表示曲线的变化率，同时也可以在物理中表现速度的变化率

提出在80米的楼上，自由落体一个物体，设重力加速的为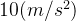 10 (m/s^2) ，于是有如下公式：

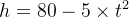$h = 80 - 5\times t^2$ (m)

从公式上看，很明显t最大为4，因为这个时后物体已经落地，下落至的离地高度为0

这时整个过程的平均速度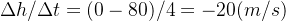： $\Delta h/\Delta t = ( 0-80 ) /4 = -20 (m/s)$

当物体落地的瞬时速度: 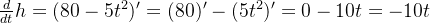$\frac{d}{dt}h=(80 - 5t^2)' = (80)' - (5t^2)' = 0 - 10t = -10t$

( 此时使用了上节课的结论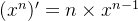， $(x^n)' = n\times x^{n-1}$ )

由于 t=4 时物体落地，所以落地时的瞬时速度为 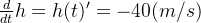$\frac{d}{dt}h = h(t)' = -40 (m/s)$

三、python的展示，找找资料，选定了用pygame来展示这个南瓜坠落的实验。

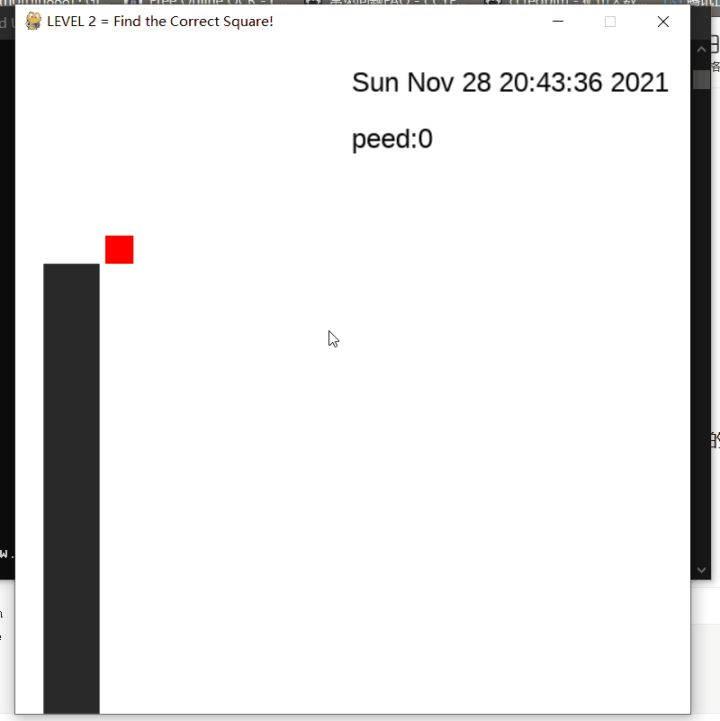
由于坐标系做的有点问题，偏移时像素没有对应到小数位，结果不很准确，不过也能说明问题了。

import random
import pygame
import math
import sys
import time

from pygame.constants import K_RETURN
from Coordinate import *
from screen import *
from XRectangle import XRectangle
from timer import Timer
def CalculateDistance(seconds, g):
    return int(1/2*g*seconds**2)
def CalculateSpeed(seconds, g):
    return seconds *g
if __name__ == "__main__":
    g = 10
    x0 = 16
    y0 = 80
    height = 5
    scr = Screen()
    clock = pygame.time.Clock()

    pygame.init()
    coordinate = Coordinate(scr, 80.0/400.0, False)
    #building = Building(5,0, 10,80,coordinate)
    building = XRectangle(5, 0, 10, 80, coordinate, scr, 0)
    ti = Timer(60, 90,24,coordinate,scr)
    speed = Timer(60, 80,24,coordinate,scr)
    rectangle = XRectangle(x0, y0, height, height, coordinate, scr, 1)
    clock = pygame.time.Clock()
    timeBegin = 0
    seconds = 0
    running = True
    xx = 0
    tmpDistY = 0
    tmpDistY1 = 0
    tmpSpeed = '0'
    tmpSeconds = 0
    dist = 0
    while running:
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                running = False
                break
            elif event.type == pygame.KEYDOWN:
                 key = event.key
                 if key == K_RETURN:
                     timeBegin = time.time()

        scr.fill()
        building.draw()
        if timeBegin!=0:
            seconds = time.time()
            seconds = seconds - timeBegin
            dist = CalculateDistance(seconds, g)
            if dist !=0 and dist <=80:
                tmpDistY = rectangle.draw_rect(0, dist)
                # this is not accurate since I can only use integer value to move
                print( 'dy/dx = ', (tmpDistY -tmpDistY1 ) / (seconds-tmpSeconds))
                if tmpSeconds!=seconds:
                   tmpSeconds = seconds
                
            else:
                rectangle.draw()
        else:
            rectangle.draw()
        ti.draw(time.ctime())
        if tmpDistY1 != tmpDistY:
            tmpSpeed = str(CalculateSpeed(seconds,g))
            speed.draw('peed:' + tmpSpeed)
            tmpDistY1 = tmpDistY
        else:
            speed.draw('peed:' + tmpSpeed)
        pygame.display.flip()
        clock.tick(40)

四、这个小程序的说明：

坐标类（用于坐标变换）Coordinate

构造函数def __init__(self, scr, uor, beginFromLeftTop):

coordinate = Coordinate(scr, 80.0/400.0, False) ，这里scr是pygame构造的窗口，uor表示80米为400个像素，方便做这个实验，beginFromLeftTop 这个变量在这个程序中为负，意思为x，y从左下角开始，实际上屏幕坐标从左上开始

函数Dist ：用于把逻辑长度比如80m变成屏幕的像素

函数XY：用于把逻辑坐标比如（5m，0m）变成屏幕坐标（ ??,?? )

长方形类XRectangle

构造函数 def __init__(self, x, y, width, height, coord, screen, color):

例如：building = XRectangle(5, 0, 10, 80, coordinate, scr, 0) 构造一个从窗口左边向右5m，从下开始0m高80米的一个黑色的矩形（颜色是个选项，0代表灰黑色，1代表红色）

def draw_rect(self,distX,distY): 重画矩形，在偏移为（distX， distY）的位置

还有timer类用来展示时间，等等，有兴趣的请查看源代码。

p.s. 敲击键盘Enter键使小方块落下。

源代码：

链接：https://pan.baidu.com/s/1-Opq7S25ANjE8Oe203AAPQ

提取码：qwmu