2023数学建模国赛A题定日镜场的优化设计- 全新思路及代码
背景资料关键信息和要点如下:
定日镜:塔式太阳能光热发电站的基本组件,由纵向转轴和水平转轴组成,用于反射太阳光。
定日镜场:由大量的定日镜组成的阵列。
集热器:位于吸收塔顶端,用于收集太阳光并转换为热能。
太阳光:并非平行光线,是一束锥形光线。
定日镜工作原理:控制定日镜的法向,使得太阳光经定日镜反射后指向集热器中心。
建设区域:在指定的地理坐标和海拔高度的圆形区域内。
集热器尺寸:高8m、直径7m的圆柱形。
定日镜尺寸:平面矩形,边长在2m至8m之间,安装高度在2m至6m之间。
其他约束:吸收塔周围100m范围内不安装定日镜;定日镜底座中心间距需大于镜面宽度+5m。
计算时点:每月21日的几个特定时刻。
请建立模型解决以下问题:
问题 1 若将吸收塔建于该圆形定日镜场中心,定日镜尺寸均为 6 m×6 m,安装高度均为4 m,且给定所有定日镜中心的位置(以下简称为定日镜位置,相关数据见附件),请计算该定日镜场的年平均光学效率、年平均输出热功率,以及单位镜面面积年平均输出热功率(光学效率及输出热功率的定义见附录)。请将结果分别按表 1 和表 2 的格式填入表格。
思路概要:本题需要根据题目给出的定义以及计算公式逐个计算特定时间节点每片定日镜片的光学效率、热功率。然后将求得数据累加除以时间以获取年平均值。
详解:问题1中给出了镜面边长
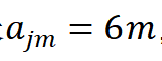
,安装高度
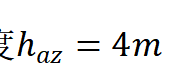
附件1中给出了各个镜面的位置平面坐标。
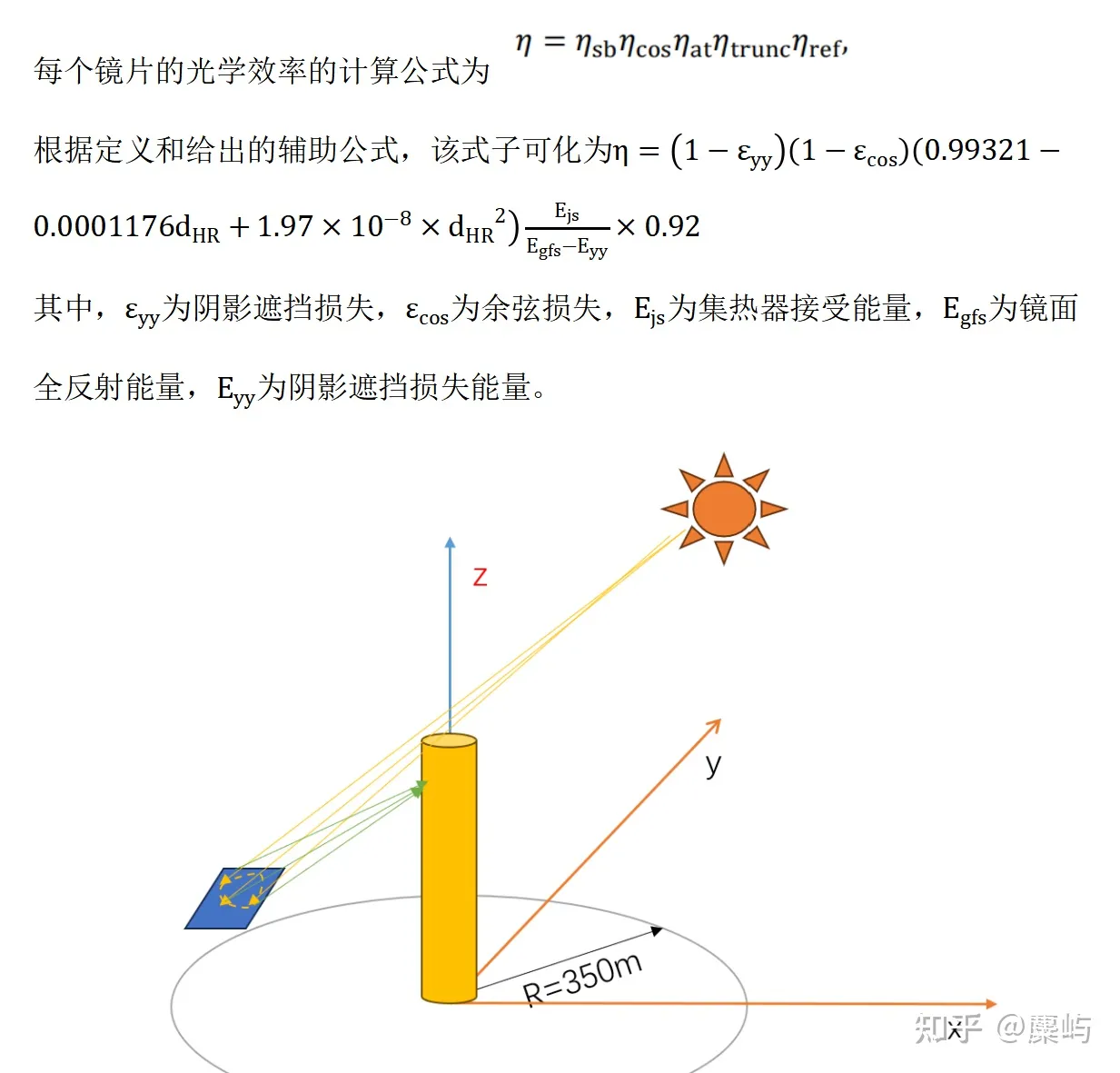
由题干背景部分给出的信息,可以知道。计划建设的镜场坐标系以圆形区域中心为原点,正东方向为x轴正向,正北方向为y轴正向,垂直于地面向上方向为 z 轴正向建立坐标系。如下图所示:
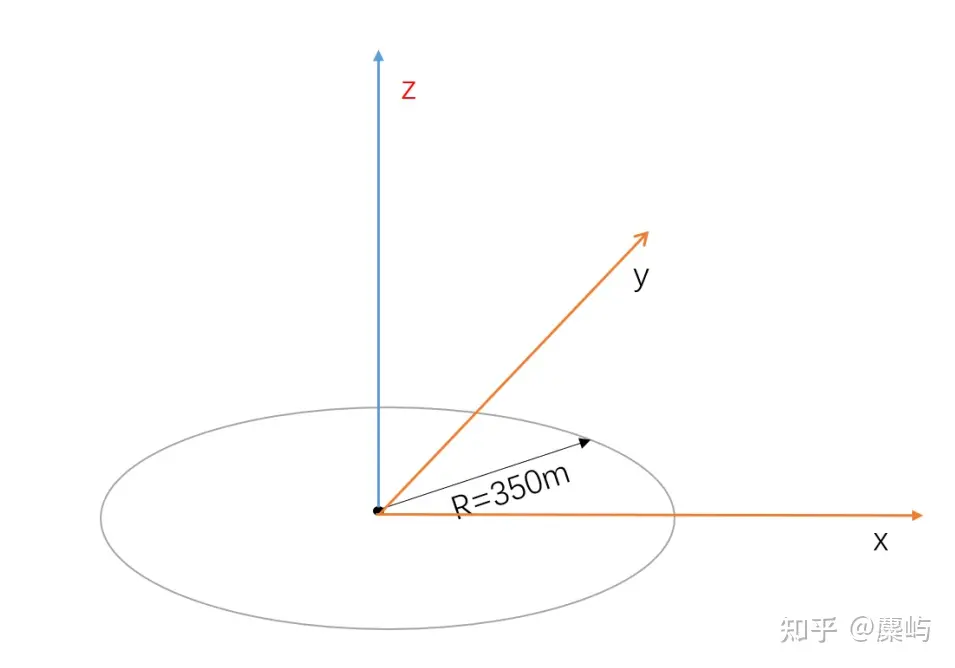
由此可得,在镜面坐标系下,各个镜面的中心位置坐标为Oi,同时,根据规划的吸收塔高度为 80 m,得到集热器中心的位置坐标为O集热(0,0,80)
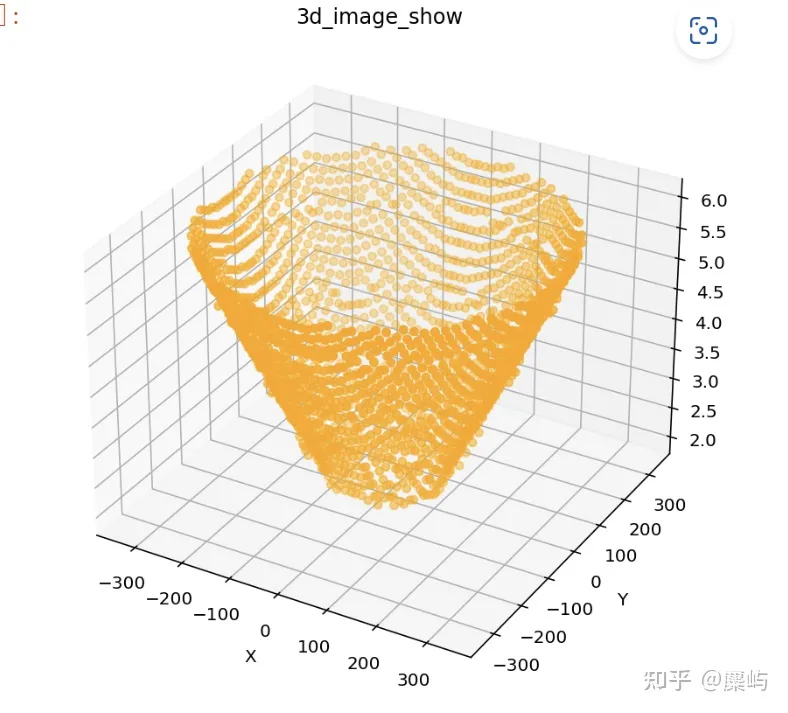
读取附件中的xy坐标数据并可视化:
import pandas as pd
import numpy as np
#读取&整理数据
data=pd.read_excel('附件.xlsx')
import matplotlib.pyplot as plt
# Plot the x and y coordinates
plt.figure(figsize=(10, 10))
plt.scatter(data['x坐标 (m)'], data['y坐标 (m)'], color='b', marker='s')
plt.xlabel('x (m)')
plt.ylabel('y (m)')
plt.title('Spatial Distribution of Points')
plt.grid(True)
plt.axis('equal')
plt.show() 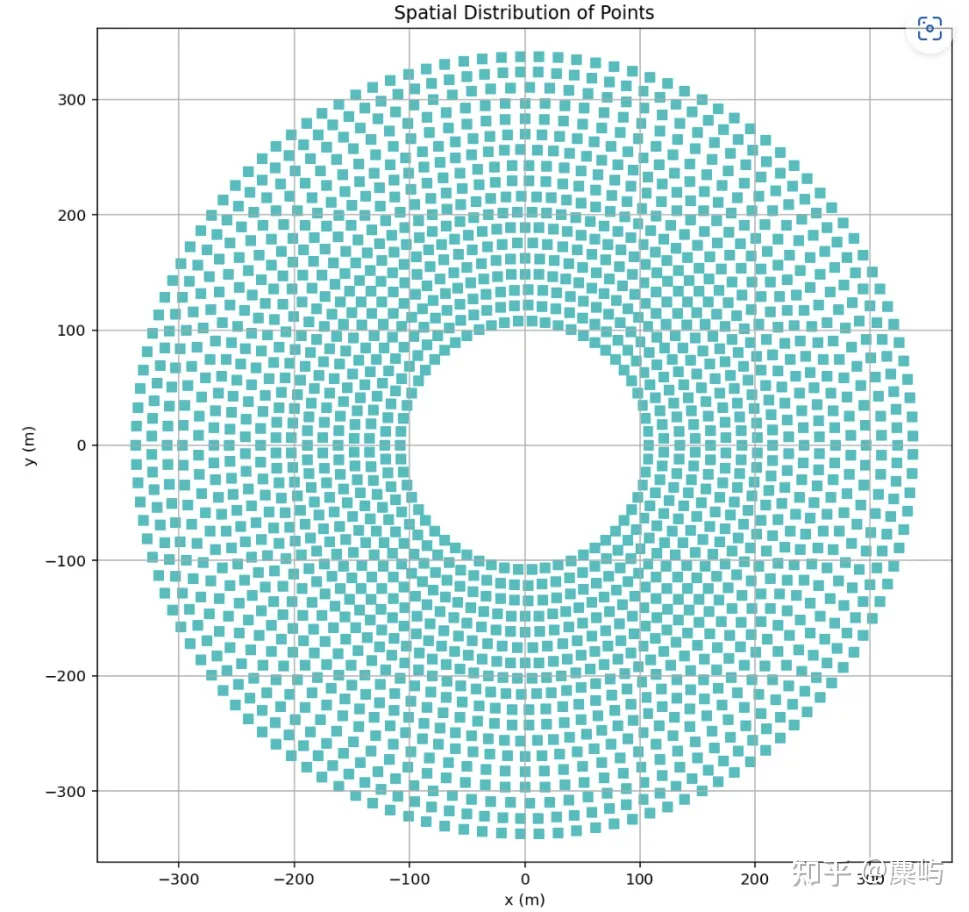
从上图可以看出,这些点分布在一个近似圆形的区域内,这与题目中提到的圆形定日镜场相吻合。
公式推导与计算
·(1)每月 21 日平均光学效率
要想计算这些损失和能量值,首先需要计算太阳的位置以及辐射能量:
import numpy as np
# 给定的参数
phi = np.deg2rad(39.4) # 当地纬度,北纬为正
times = [9, 10.5, 12, 13.5, 15] # 计算的时间点
spring_equinox = 21 # 春分日期
days_in_month = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31] # 每月的天数
# 计算对应每个计算时间点的天数 D
months = list(range(1, 13))
D_values = [-59,-28,0]+[sum(days_in_month[2:i]) for i in range(3,12)]
#D_values
# 根据公式计算太阳高度角和太阳方位角
alpha_s = [] #高度角
gamma_s = [] #方位角
for D in D_values:
delta = np.arcsin(np.sin(2 * np.pi * D / 365) * np.sin(np.deg2rad(23.45)))
for ST in times:
omega = np.pi / 12 * (ST - 12)
alpha_s_value = np.arcsin(np.cos(delta) * np.cos(phi) * np.cos(omega) + np.sin(delta) * np.sin(phi))
gamma_s_numerator = np.sin(delta) - np.sin(alpha_s_value) * np.sin(phi)
gamma_s_denominator = np.cos(alpha_s_value) * np.cos(phi)
gamma_s_value = np.arccos(gamma_s_numerator / gamma_s_denominator)
alpha_s.append(alpha_s_value)
gamma_s.append(gamma_s_value)
alpha_s, gamma_s 后续计算 略
问题 2 按设计要求,定日镜场的额定年平均输出热功率(以下简称额定功率)为 60 MW。
若所有定日镜尺寸及安装高度相同,请设计定日镜场的以下参数:吸收塔的位置坐标、定日镜尺寸、安装高度、定日镜数目、定日镜位置,使得定日镜场在达到额定功率的条件下,单位镜面面积年平均输出热功率尽量大。请将结果分别按表 1、2、3 的格式填入表格,并将吸收塔的位置坐标、定日镜尺寸、安装高度、位置坐标按模板规定的格式保存到 result2.xlsx 文件中。


后续略
问题 3 如果定日镜尺寸可以不同,安装高度也可以不同,额定功率设置同问题 2,请重新设计定日镜场的各个参数,使得定日镜场在达到额定功率的条件下,单位镜面面积年平均输出热功率尽量大。请将结果分别按表 1、表 2 和表 3 的格式填入表格,并将吸收塔的位置坐标、各定日镜尺寸、安装高度、位置坐标按模板规定的格式保存到 result3.xlsx 文件中。
思路概要:这里前边可以采用问题2同样的思路,由于目标都是使得输出热功率尽量大(即光学效率越高越好),所以可以沿用问题2中确定下来的一些参数。接着针对不同的尺寸与安装高度,建立新的输出热功率计算模型。注意这里需要考虑一些限制约束条件安装高度必须保证镜面在绕水平转轴旋转时不会触及地面。(》ajm/2)

完整版请戳
链接:https://pan.baidu.com/s/1zhW45iASyzlyCChCLoH0Kw 提取码:mz3p