MINIEYE笔试第一题：堆方块求表面积

注意：

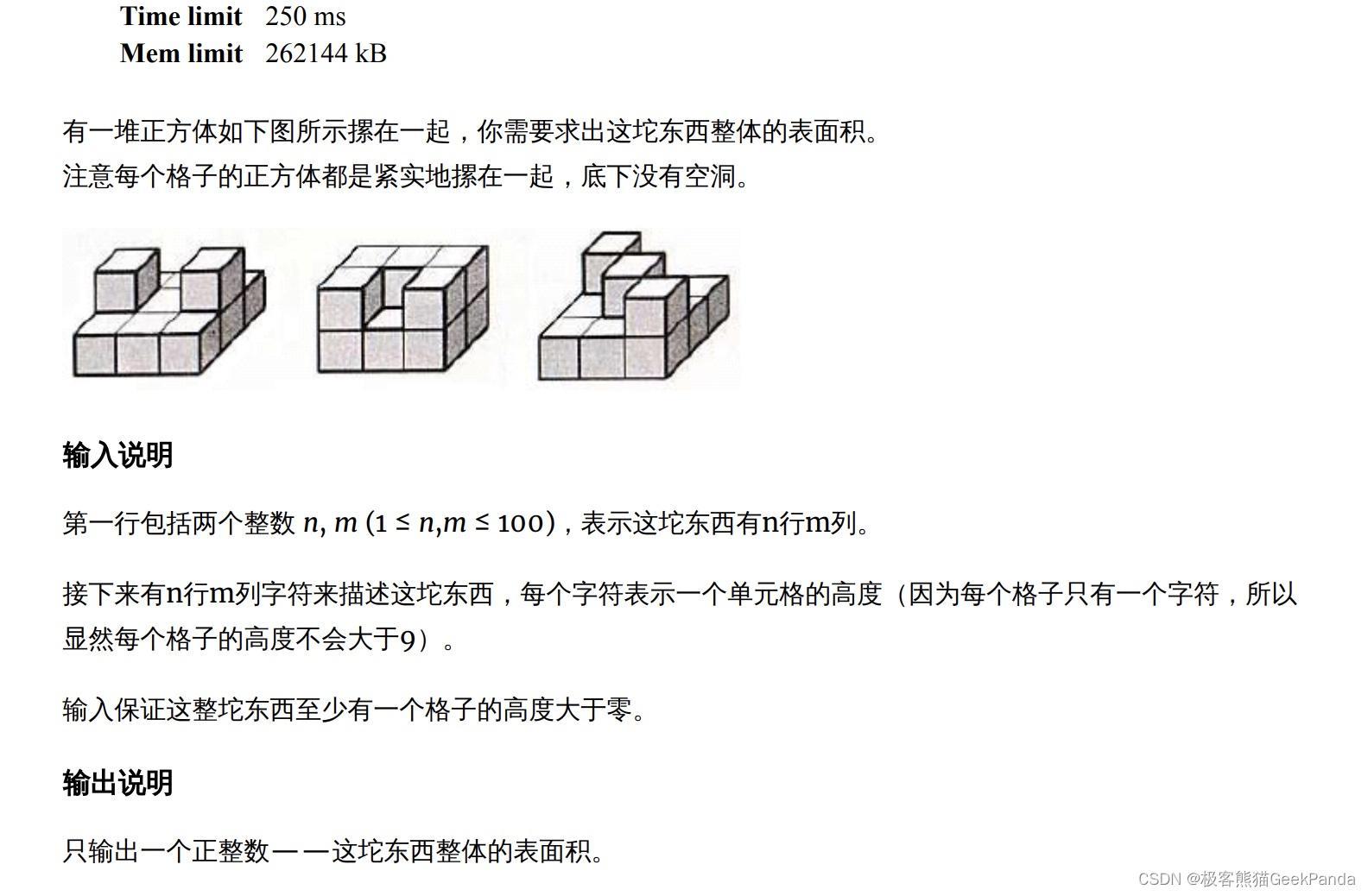
求一个立方体堆积的多面体的全部表面积。不能简单通过前后左右上下6个面的投影得到，要考虑中间可能有凹陷，凹陷部分会多出表面积。

应当使用减法：先求出所有小方块的6表面积之和，假设它们前后左右不重叠，然后遍历行和列，按照前后和左右，相邻两个方块，高度小的一边会被重叠掉（记高度小的高度为x），应减去2*x。

#include <iostream>
#include <string>
#include <vector>
#include <cmath>
#include <algorithm>

int Solution(int n, int m, std::vector<std::vector<int> > &vec){
        int s=0,sum=0,s_left=0,s_pre=0,s_above=0;
        for(int i = 0;i < n;++i){
            for(int j = 0; j < m; ++j){
                if(vec[i][j] > 0)
                    sum += 4 * vec[i][j] + 2;
                if(j + 1 < n)
                    s_left += 2 * std::min(vec[i][j+1], vec[i][j]);
                if(i + 1 < n)
                    s_pre += 2 * std::min(vec[i+1][j], vec[i][j]);
            }  
        }
        s = sum- s_left -s_pre;
        return s;
}

int main(){
    int n, m;
    std::cin >> n >> m;
    std::vector<std::vector<int> > vec(n);
    for(int i = 0; i < n; ++i){
        std::string str;
        std::cin >> str;
        int num = stoi(str);
        int col = m;
        while(col > 0){
            vec[i].push_back(num / pow(10, col-1));
            num %= int(pow(10, col-1));
            --col;
        }
    }
    std::cout << Solution(n, m, vec) << std::endl;
    return 0;
}