flash attention论文及源码学习

​

论文

attention计算公式如下
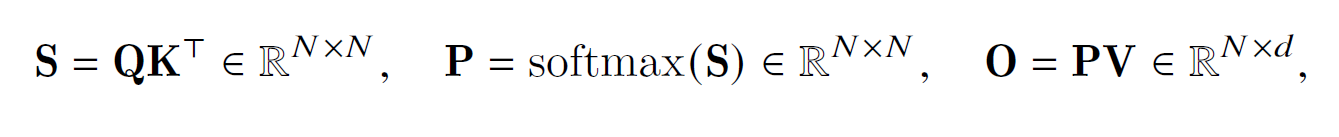
在这里插入图片描述

传统实现需要将S和P都存到HBM，需要占用 O ( N 2 ) O(N^{2}) O(N2)内存，计算流程为
在这里插入图片描述

因此前向HBM访存为 O ( N d + N 2 ) O(Nd + N^2) O(Nd+N2)，通常N远大于d，GPT2中N=1024，d=64。HBM带宽较小，因此访存会成为瓶颈。
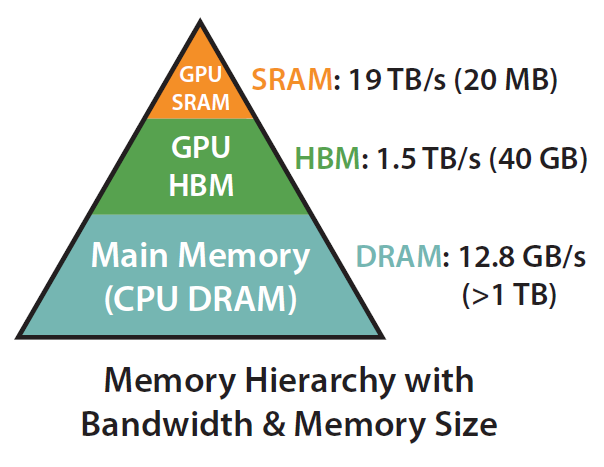
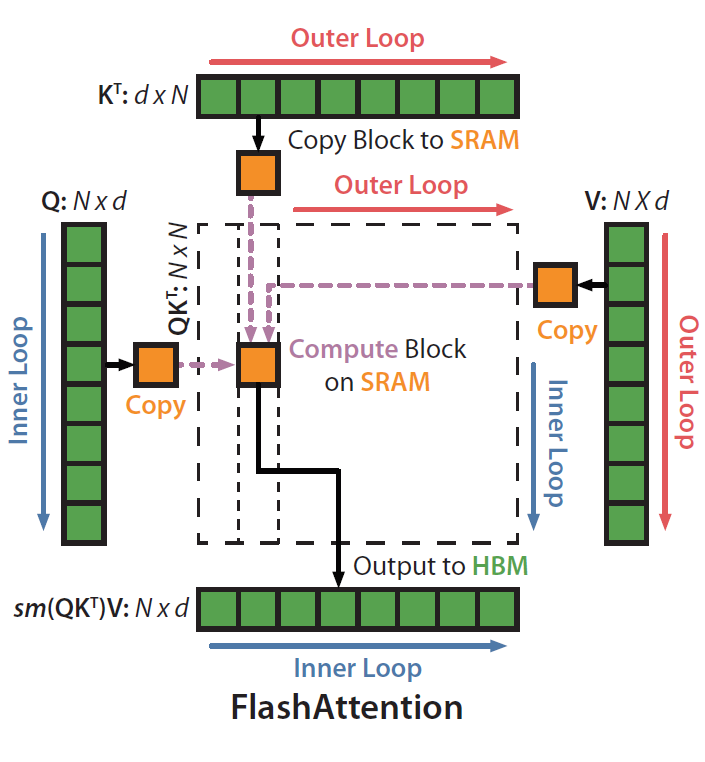
在这里插入图片描述

该论文主要出发点就是考虑到IO的影响，降低内存占用和访问，主要贡献点为：

  • 重新设计了计算流程，使用softmax tiling的方法执行block粒度的计算
  • 不需要存储矩阵P，只存储归一化因子，再反向的时候可以快速的recompute

softmax tiling的整体流程如下图，外层第j次循环拿到K矩阵的第j个block k j kj kj，内层第i次循环拿到Q矩阵的第i个block Q i Qi Qi，计算得到S和P，然后再和 V j Vj Vj相乘得到 O i Oi Oi

在这里插入图片描述

然后看下如何计算出softmax。考虑数值稳定性的softmax的传统计算流程如下，需要减去当前行的最大值
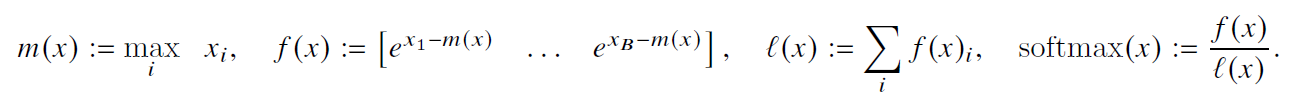
在这里插入图片描述

这里的max和sum都需要一行的完整结果。

而flash attention的流程基于递推实现block粒度的计算：
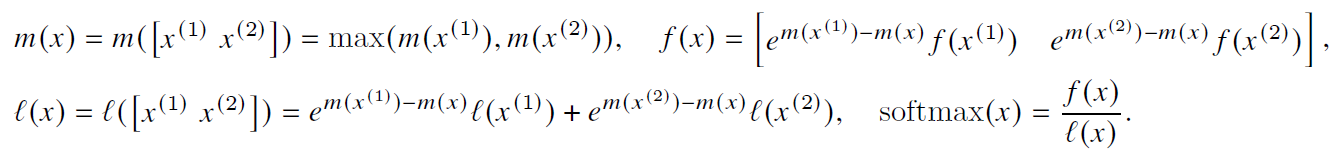
在这里插入图片描述

单看S的一行，假设 m ( x ) m(x) m(x)为执行到第i个block即 S ( i ) S(i) S(i)的最大值，现在执行第i + 1个block S ( i + 1 ) S(i + 1) S(i+1)，那么新的 m ( x ) = m a x ( m ( x ) , m ( S ( i + 1 ) ) ) m(x) = max(m(x), m(S(i + 1))) m(x)=max(m(x),m(S(i+1)))，由于最大值发生了变化，因此之前i个block对应的f(x)要进行修正，之前减去的是 m ( x ( 1 ) ) m(x^{(1)}) m(x(1))，因此要将他加回来，再减去新的 m ( x ) m(x) m(x)，即 e m ( x ( 1 ) − m ( x ) ) f ( x ( 1 ) ) e^{m({x^{(1)} - m(x))}} f(x^{(1)}) em(x(1)−m(x))f(x(1))，同理对于sum，最后就可以得到softmax，完整流程如下
在这里插入图片描述

因此内存占用为O(N)，假设share mem大小为M，那么对于HBM的访存为 O ( N 2 d 2 M − 1 ) O(N^{2}d^{2}M^{-1}) O(N2d2M−1)

A100 Tensor Core

为了加速深度学习里的fc和卷积，nvidia引入了Tensor Core到gpu里，单个sm如下所示
​


在这里插入图片描述

图 2-1
A100的一个sm有4个Tensor Core，以FP16/FP32混合精度为例，每个Tensor Core每个周期可以计算256个FP16 FMA，即8x4x8的矩阵运算。除了通过cublas，cudnn等官方库使用Tensor Core之外，nv还提供了WMMA和mma PTX两种方式使用Tensor Core，由于flash attention用的是mma PTX，所以后续只介绍下mma PTX。 矩阵的乘累加形为D = A * B + C，其中A和B不支持FP32，输入的FP32会被转为同样位宽的TF32，C和D支持FP32，详细类型见下表，其中mma.sync就是执行了一次矩阵乘累加

在这里插入图片描述

图 2-2
mma为warp-level的操作，矩阵乘由32线程一起完成，但是存储是和cuda core共享，也就是说A和B需要分布式的存储在32线程的寄存器中，每个线程存储了原始矩阵的一部分，称为一个fragment，这个分布式存储的过程需要用户显式完成，然后Tensor Core会访问所有线程寄存器完成矩阵运算，以fp16的16x8x16的A为例，数据在warp中的分布如下所示

在这里插入图片描述

图 2-3
假设A的一个tile已经通过LDG从global mem加载到了shared mem中，为了完成上图的数据排布，我们可以使用LDS指令加载数据，但是由于数据分布不是连续的，所以要执行4次LDS，为了解决这个问题，nvidia提供了一个指令为ldmatrix，可以一跳指令完成16x16的矩阵加载，流程如下，每个thread读入128b，然后将128b写入到4个lane对应的寄存器中，以T0为例，会读入矩阵第一行的前8个FP16，写入到T0，T1，T2，T3对应的寄存器中

在这里插入图片描述

图 2-4

​

在这里插入图片描述

图 2-5
值得注意的是，假设shared mem中为连续存储，这里将发生bank冲突，gpu的shared mem中有32bank，每个bank 4字节，由于每个线程读取128b，因此每个线程占4个bank，所以整个读取过程将分为4次，第一次为T0-T7，第二次为T8-T15，第三次为T16-T23，第四次为T24-T31，如果shared mem中为连续存储，如下图，数字表示原始16x16矩阵中的行和列，那么在第一次读取中，绿色部分为T0读，蓝色部分为T4读，将发生冲突，shared mem利用率只有一半。

在这里插入图片描述

图 2-6
为了解决这个问题，cutlass使用了xor swizzle的方法避免bank冲突，如下所示

在这里插入图片描述

图 2-7
# 源码流程 ## 两层循环流程控制 前向入口为mha_fwd 
std::vector<at::Tensor>
mha_fwd(const at::Tensor &q,         // total_q x num_heads x head_size, total_q := \sum_{i=0}^{b} s_i
        const at::Tensor &k,         // total_k x num_heads x head_size, total_k := \sum_{i=0}^{b} s_i
        const at::Tensor &v,         // total_k x num_heads x head_size, total_k := \sum_{i=0}^{b} s_i
        at::Tensor &out,             // total_q x num_heads x head_size, total_k := \sum_{i=0}^{b} s_i
        const at::Tensor &cu_seqlens_q,  // b+1
        const at::Tensor &cu_seqlens_k,  // b+1
        const int max_seqlen_q_,
        const int max_seqlen_k_,
        const float p_dropout,
        const float softmax_scale,
        const bool zero_tensors,
        const bool is_causal,
        const bool return_softmax,
        const int num_splits,
        c10::optional<at::Generator> gen_)

q，k，v的shape均为[total_q, num_heads, head_size]，dtype为FP16或者BF16，total_q就是按照batchsize累加token，cu_seqlens_q为每个batch的token数量的前缀和
不加说明的话假设后续total_q和total_k相等，head_size为32，dtype为FP16

   Launch_params<FMHA_fprop_params> launch_params(dprops, stream, is_dropout, return_softmax);
   at::Tensor o_tmp;
   if (loop) { o_tmp = torch::empty({total_q, num_heads, head_size}, opts.dtype(at::kFloat)); }
   auto softmax_lse = torch::empty({batch_size, num_heads, max_seqlen_q}, opts.dtype(at::kFloat));
   set_params_fprop(launch_params.params,
                    batch_size,
                    max_seqlen_q,
                    max_seqlen_k,
                    num_heads,
                    head_size,
                    q, k, v, out,
                    cu_seqlens_q.data_ptr(),
                    cu_seqlens_k.data_ptr(),
                    loop ? o_tmp.data_ptr() : nullptr,
                    return_softmax ? s.data_ptr() : nullptr,
                    softmax_lse.data_ptr(),
                    p_dropout,
                    softmax_scale,
                    is_causal,
                    num_splits);

Launch_params里最核心的就是params，即FMHA_fprop_params，保存了kernel的上下文信息，比如Q，K，V的指针，stride，shape等信息，这里通过set_params_fprop保存了context。

void run_fmha_fwd_hdim32(Launch_params<FMHA_fprop_params> &launch_params) {
    ...
    using Kernel_traits = FMHA_kernel_traits<128, 32, 16, 1, 4, 0x08u, elem_type>;
    run_fmha_fwd_loop<Kernel_traits>(launch_params);
    ...
}

FMHA_kernel_traits 为当前规模下的各种类型定义，先看下Q相关的几个，注释写了当前规模下的值，elem_type为__half

        // 128     32        16      1            4
template<int S, int D, int STEP, int WARPS_M, int WARPS_N, uint32_t FLAGS = 0x08u, typename elem_type_=__half>
struct FMHA_kernel_traits {
    using Cta_tile_p = fmha::Cta_tile_extd<STEP, S, D, WARPS_M, WARPS_N, 1>;
    ...
    using Gmem_tile_q = fmha::Gmem_tile_qkv<Cta_tile_p, fmha::BITS_PER_ELEMENT_A, STEP, D>;
    using Smem_tile_q = fmha::Smem_tile_a<Cta_tile_p, fmha::Row, Gmem_tile_q::BYTES_PER_LDG, 2>;
    ...
}

cta_tile表示一个计算矩阵乘的cta线程怎么排布，去处理一个多大的tile，对于第一个矩阵乘Cta_tile_p相关变量见注释

template<
    // The number of rows in the CTA tile.  
    int M_,       // STEP  ：16
    // The number of cols in the CTA tile.
    int N_,       // S  ：128
    // The number of elements in the the K dimension of the GEMM loop.
    int K_,       // D ：32
    // The number of rows of warps.
    int WARPS_M_, // 4
    // The number of cols of warps.
    int WARPS_N_, // 1
    // The number of warps in the K dimension of the GEMM loop.
    int WARPS_K_> // 1
struct Cta_tile_ {

    static constexpr int M = M_, N = N_, K = K_; 
    // The number of warps.
    static constexpr int WARPS_M = WARPS_M_, WARPS_N = WARPS_N_, WARPS_K = WARPS_K_;
    // The number of warps per CTA.
    static constexpr int WARPS_PER_CTA = WARPS_M * WARPS_N * WARPS_K;
    // The number of threads per warp.
    static constexpr int THREADS_PER_WARP = 32; 
    // The number of threads per CTA.
    static constexpr int THREADS_PER_CTA = WARPS_PER_CTA * THREADS_PER_WARP;
};

然后通过run_fmha_fwd_loop启动kernel，简便起见，假设num_splits为1，所以一共启动了[batch_size, num_head]个cta，每个cta负责一个batch里的一个head

template<typename Kernel_traits>
void run_fmha_fwd_loop(Launch_params<FMHA_fprop_params> &launch_params) {
    ...
    dim3 grid(launch_params.params.b, launch_params.params.h, launch_params.params.num_splits);
    kernel<<<grid, Kernel_traits::THREADS, smem_size, launch_params.stream>>>(
        launch_params.params);
    FMHA_CHECK_CUDA(cudaPeekAtLastError());
    ...
}

然后看下kernel，这里就是论文中的外层循环，每次计算完成k矩阵的一个block计算，blockIdx.x表示哪个batch，blockIdx.y表示哪个head。

template<typename Kernel_traits, bool Is_dropout, bool Is_causal, bool Return_softmax, typename Params>
inline __device__ void device_1xN_loop(const Params &params) {

    // The block index for the batch.
    const int bidb = blockIdx.x;
    // The block index for the head.
    const int bidh = blockIdx.y;
    // The thread index.
    const int tidx = threadIdx.x;
    auto seeds = at::cuda::philox::unpack(params.philox_args);
    Philox ph(std::get<0>(seeds), 0, std::get<1>(seeds) + (bidb * params.h + bidh) * 32 + tidx % 32);
    constexpr int M = Kernel_traits::Cta_tile_p::M;
    const int STEPS = (params.seqlen_q + M - 1) / M;

    constexpr int blocksize_c = Kernel_traits::Cta_tile_p::N;
    if (params.seqlen_k == blocksize_c) {
        fmha::device_1xN_<Kernel_traits, Is_dropout, Is_causal, Return_softmax, true, true>(params, bidb, bidh, STEPS, ph, 0);
    } else {
        const int max_loop_steps = (params.seqlen_k + blocksize_c - 1) / blocksize_c;
        fmha::device_1xN_<Kernel_traits, Is_dropout, Is_causal, Return_softmax, true, false>(params, bidb, bidh, STEPS, ph, 0);
        for (int loop_step_idx = 1; loop_step_idx < max_loop_steps - 1; loop_step_idx++) {
            fmha::device_1xN_<Kernel_traits, Is_dropout, Is_causal, Return_softmax, false, false>(params, bidb, bidh, STEPS, ph, loop_step_idx);
        }
        fmha::device_1xN_<Kernel_traits, Is_dropout, Is_causal, Return_softmax, false, true>(params, bidb, bidh, STEPS, ph, max_loop_steps - 1);
    }
}

然后是最核心的一次内层循环的流程

template<typename Kernel_traits, bool Is_dropout, bool Is_causal, bool Return_softmax, bool Is_first, bool Is_last, typename Params, typename Prng>
inline __device__ void device_1xN_(const Params &params, const int bidb, const int bidh, int steps, Prng &ph, const int loop_step_idx) {
    ...
    
    extern __shared__ char smem_[];

    const int tidx = threadIdx.x;
    
    ...
    const BlockInfoPadded<Kernel_traits::THREADS> binfo(params, bidb, bidh, tidx);
    // if( binfo.stop_early() ) return;
    if( binfo.stop_early(loop_step_idx * Cta_tile_p::N) ) return;
    Gemm1 gemm_q_k(smem_, tidx);
    ...
  }

BlockInfoPadded的核心就是sum_s_q和actual_seqlen_q，分别表示前边的batch一共有多少token，和当前batch有多少token

template<int THREADS_PER_CTA>
struct BlockInfoPadded {

    template<typename Params>
    __device__ BlockInfoPadded(const Params &params,
                               const int bidb,
                               const int bidh,
                               const int tidx)
        : bidb(bidb), bidh(bidh), h(params.h) {

        // The block index.
        sum_s_k = params.cu_seqlens_k[bidb];
        actual_seqlen_k = params.cu_seqlens_k[bidb + 1] - sum_s_k;
        sum_s_q = params.cu_seqlens_q[bidb];
        actual_seqlen_q = params.cu_seqlens_q[bidb + 1] - sum_s_q;

        tidx_global = (bidb * params.h + bidh) * THREADS_PER_CTA + tidx;
    }
    ...
};

global mem到寄存器

然后实例化gemm_q_k，负责第一个gemm，后边介绍，即QK，后边介绍。gmem_q负责将Q矩阵从global mem中load到寄存器

inline __device__ void device_1xN_(const Params &params, const int bidb, const int bidh, int steps, Prng &ph, const int loop_step_idx) {
    ...
    Gemm1 gemm_q_k(smem_, tidx);
    // Allocate the global memory tile loader for Q.
    Gmem_tile_q gmem_q(params.q_ptr, params.q_row_stride_in_elts, params.q_head_stride_in_elts,
                       params.d, binfo, tidx, true);
    ...
}

using Gmem_tile_q = fmha::Gmem_tile_qkv<Cta_tile_p, fmha::BITS_PER_ELEMENT_A, STEP, D>;

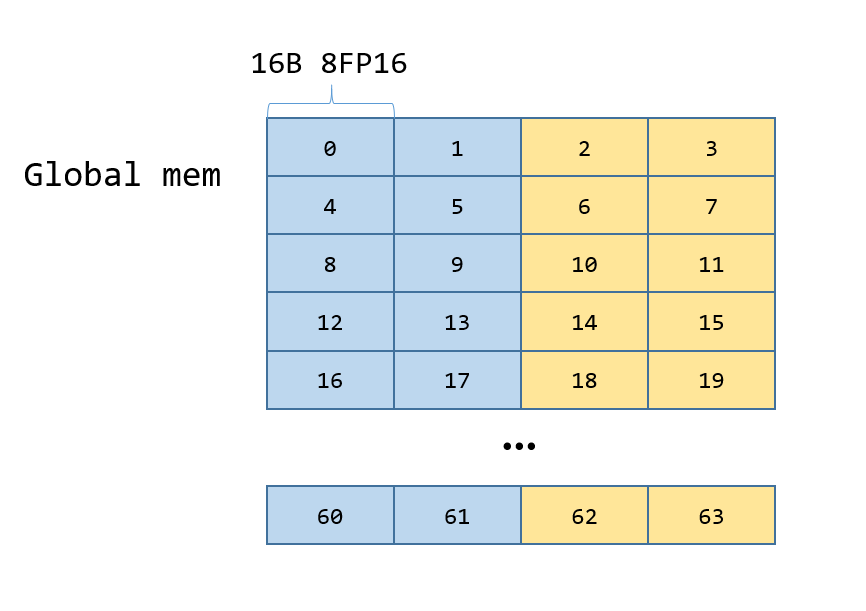
先看下Gmem_tile_q，这里ROWS和COLS为一次处理的block大小，对于q矩阵来说为16x32，BITS_PER_ELEMENT为q矩阵中每个元素为多少bit，由于为FP16，这里为16，BYTES_PER_LDGS_ 表示一个线程一次load的字节数，这里为16字节，一行需要4个线程去load

template<
    // The dimensions of the tile computed by the CTA.
    typename Cta_tile_,
    // The number of bits per element.
    int BITS_PER_ELEMENT,
    // The number of rows of Q, K or V loaded by this tile.
    int ROWS_,
    // The number of columns.
    int COLS,
    int BYTES_PER_LDGS_ = 16
>

然后看下构造函数，row和col计算出当前线程在这个tile中需要从哪行哪里开始load，通过binfo.sum_s_q + row跳过前边batch的token并定位到当前应该处理的是哪个token，row_stride就是num_heads x head_size，然后再跳过前边的head，再加上col就可以定位到当前起始的位置，即ptr

template< typename BInfo >
inline __device__ Gmem_tile_qkv(void *ptr_, const uint32_t row_stride_in_elts,
                                const uint32_t head_stride_in_elts, const int headdim,
                                const BInfo &binfo, const int tidx, bool use_seqlen_q)
    : row_stride_in_bytes(row_stride_in_elts * BYTES_PER_ELEMENT)
    , actual_seqlen(use_seqlen_q ? binfo.actual_seqlen_q : binfo.actual_seqlen_k)
    , ptr(reinterpret_cast<char *>(ptr_))
    , tidx_(tidx)
    , col_predicate((tidx % THREADS_PER_ROW) * (BYTES_PER_LDG / BYTES_PER_ELEMENT) < headdim) {

    // Compute the position in the sequence (within the CTA for the moment).
    int row = tidx / THREADS_PER_ROW;
    // Compute the position of the thread in the row.
    int col = tidx % THREADS_PER_ROW;

    uint32_t row_offset = (uint32_t)(((use_seqlen_q ? binfo.sum_s_q : binfo.sum_s_k) + row) * row_stride_in_bytes);
    row_offset += (uint32_t)(binfo.bidh * head_stride_in_elts * BYTES_PER_ELEMENT);

    // Assemble the final pointer.
    ptr += row_offset + col * BYTES_PER_LDG;
}

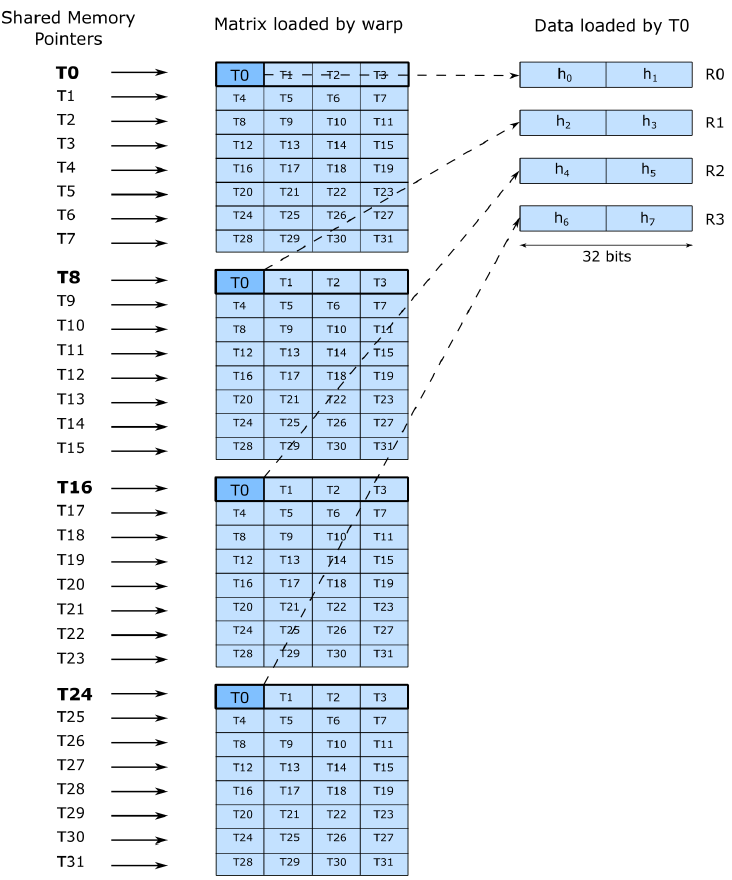
Gmem_tile_qkv的load就是从global mem加载到寄存器的过程，LDGS表示load当前tile需要几次，对于q矩阵为1，preds表示当前线程是否需要load对应的位置，由于q为16x32，因此只有前64线程会执行load，由于一个线程一次load16字节，所以这里使用uint4去load，结果存在了寄存器fetch_中。

inline __device__ void load() {
    int row_ = tidx_ / THREADS_PER_ROW;
    const void *ptrs[LDGS];
    uint32_t preds[LDGS];
    #pragma unroll
    for( int ii = 0; ii < LDGS; ++ii ) {
        ptrs[ii] = ptr + (uint32_t)ii * ROWS_PER_LDG * row_stride_in_bytes;
        preds[ii] = col_predicate && ((row_ + ii * ROWS_PER_LDG) < min(ROWS, actual_seqlen));
        fetch_[ii] = make_uint4(0, 0, 0, 0);
    }

    Ldg_functor<uint4, LDGS> fct(fetch_, ptrs);
    #pragma unroll
    for( int ii = 0; ii < LDGS; ++ii ) {
        fct.load(ii, preds[ii]);
    }
}

template< typename Smem_tile >
    inline __device__ void commit(Smem_tile &smem_tile) {
        smem_tile.store(fetch_);
}

inline __device__ void ldg(uint4 &dst, const void *ptr) {
    dst = *reinterpret_cast<const uint4*>(ptr);
}

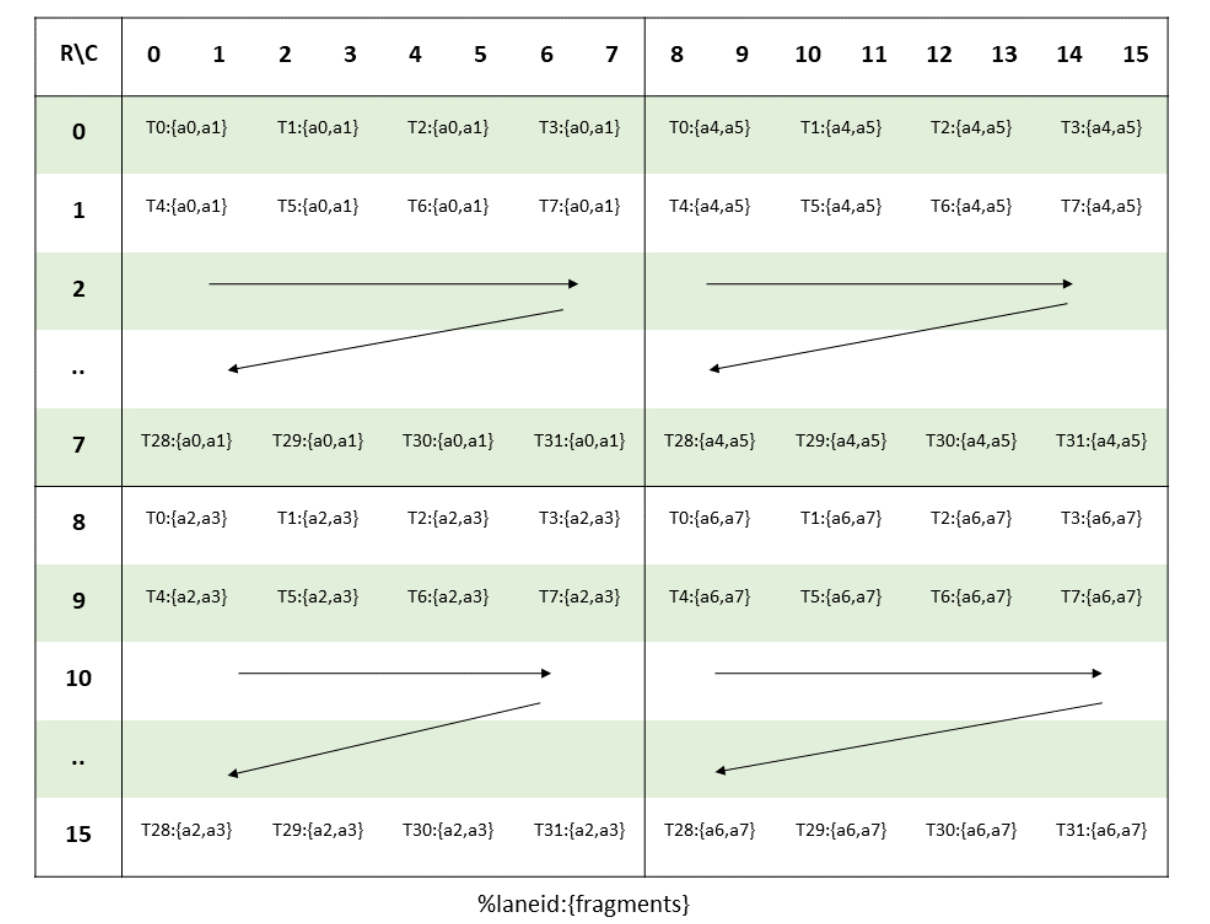
这一过程如下图所示，一个方块表示16B，方块中数字表示线程号，蓝色为第一个16x16矩阵，黄色为第二个16x16矩阵。
在这里插入图片描述

图 3-1
## 寄存器到共享内存 然后回看内循环流程，先触发q，k，v从global mem load的过程，然后将q，v加载到共享内存 
inline __device__ void device_1xN_(const Params &params, const int bidb, const int bidh, int steps, Prng &ph, const int loop_step_idx) {
    ...
    gmem_k.load();
    // Trigger the loads for Q.
    gmem_q.load();
    // Trigger the loads for V.
    gmem_v.load();
    if (!Is_first) { __syncthreads(); }
    ...
    // Commit the data for Q and V to shared memory.
    gmem_q.commit(gemm_q_k.smem_q);
    gmem_v.commit(smem_v);
}

smem_q的类型为Smem_tile_q，继承关系如下

template<
    // The description of the tile computed by this CTA.
    typename Cta_tile,
    // The number of rows in the 2D shared memory buffer.
    int M_,
    // The number of cols.
    int N_,
    // The size in bits of each element.
    int BITS_PER_ELEMENT_,
    // The number of bytes per STS.
    int BYTES_PER_STS_ = 16,
    // The number of buffers. (Used in multistage and double buffer cases.)
    int BUFFERS_PER_TILE_ = 1,
    // Do we enable the fast path for LDS.128 and friends.
    int ENABLE_LDS_FAST_PATH_ = 0,
    // The number of rows that are used for the XOR swizzling to allow fast STS/LDS.
    int ROWS_PER_XOR_PATTERN_ = 8,
    // The number of cols that are used for the XOR swizzling to allow fast STS/LDS.
    int COLS_PER_XOR_PATTERN_ = 1,
    // Use or not predicates
    bool USE_PREDICATES_ = true
>
struct Smem_tile_without_skews

template<
    // The dimensions of the tile computed by the CTA.
    typename Cta_tile,
    // The size of the STS.
    int BYTES_PER_STS,
    // The number of buffers per tile.
    int BUFFERS_PER_TILE,
    // How many rows to use for the XOR pattern to avoid bank conflicts?
    int ROWS_PER_XOR_PATTERN_ = Rows_per_xor_pattern_row_a<Cta_tile::K>::VALUE
>
struct Smem_tile_row_a : public Smem_tile_without_skews<Cta_tile,
                                                               Cta_tile::M,
                                                               Cta_tile::K,
                                                               fmha::BITS_PER_ELEMENT_A,
                                                               BYTES_PER_STS,
                                                               BUFFERS_PER_TILE,
                                                               0,
                                                               ROWS_PER_XOR_PATTERN_,
                                                               1> 
                                                               

template<
    // The dimensions of the tile computed by the CTA.
    typename Cta_tile,
    // The size of the STS.
    int BYTES_PER_STS,
    // The number of buffers per tile.
    int BUFFERS_PER_TILE
>
struct Smem_tile_a<Cta_tile, Row, BYTES_PER_STS, BUFFERS_PER_TILE>
    : public Smem_tile_row_a<Cta_tile,
                                    BYTES_PER_STS,
                                    BUFFERS_PER_TILE> {
    // The base class.
    using Base = Smem_tile_row_a<Cta_tile, BYTES_PER_STS, BUFFERS_PER_TILE>;

    // Ctor.
    inline __device__ Smem_tile_a(void *smem, int tidx) : Base(smem, tidx) {
    }
};

先看下构造函数，主要就是设置当前线程应该写哪里

inline __device__ Smem_tile_without_skews(void *smem, int tidx)
    : smem_(__nvvm_get_smem_pointer(smem)), tidx_(tidx) {

    // The row written by a thread. See doc/mma_smem_layout.xlsx.
    int smem_write_row = tidx / THREADS_PER_ROW;

    // The XOR pattern.
    int smem_write_xor = smem_write_row % ROWS_PER_XOR_PATTERN * COLS_PER_XOR_PATTERN;
    // Compute the column and apply the XOR pattern.
    int smem_write_col = (tidx % THREADS_PER_ROW) ^ smem_write_xor;

    // The offset.
    this->smem_write_offset_ = smem_write_row*BYTES_PER_ROW + smem_write_col*BYTES_PER_STS;

}

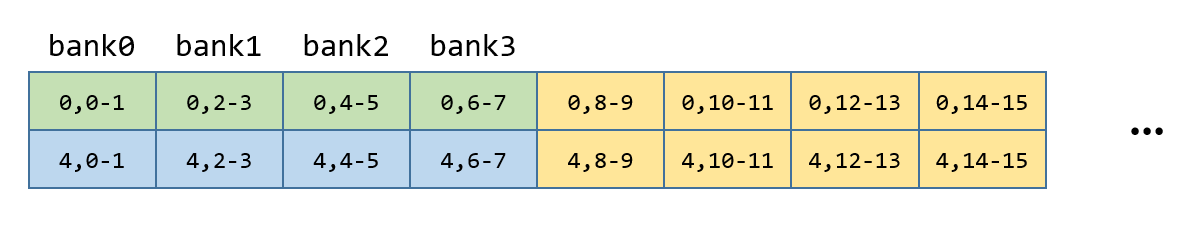
gmem的commit其实执行的就是smem的store，由于q矩阵每个线程只需要store一次，即N为1，因此只是在smem_write_offset_ 处写一次即可。

template< int N >
inline __device__ void compute_store_pointers(uint32_t (&ptrs)[N]) {
    #pragma unroll
    for( int ii = 0; ii < N; ++ii ) {
        // Decompose the STS into row/col.
        int row = ii / STS_PER_ROW;
        int col = ii % STS_PER_ROW;

        // Assemble the offset.
        int offset = smem_write_offset_ + row*ROWS_PER_STS*BYTES_PER_ROW;

        // Take the column into account.
        if( STS_PER_ROW > 1 ) {
            offset += col*THREADS_PER_ROW*BYTES_PER_STS;
        }
        // Apply the XOR pattern if needed.
        if( ROWS_PER_STS < ROWS_PER_XOR_PATTERN ) {
            const int m = row * ROWS_PER_STS % ROWS_PER_XOR_PATTERN;
            offset ^= m * COLS_PER_XOR_PATTERN * BYTES_PER_STS;
        }
        ptrs[ii] = smem_ + offset;
    }
}

template< int N >
inline __device__ void store(const Store_type (&data)[N], uint64_t = 0) {
    uint32_t smem_ptrs[N];
    this->compute_store_pointers(smem_ptrs);
    // Trying to reduce the shared mem for Q from 4KB per buffer to 2KB per buffer.
    if (!PARTIAL_STORE || (tidx_ / THREADS_PER_ROW < ROWS)) {
        sts(smem_ptrs, data);
    }
}

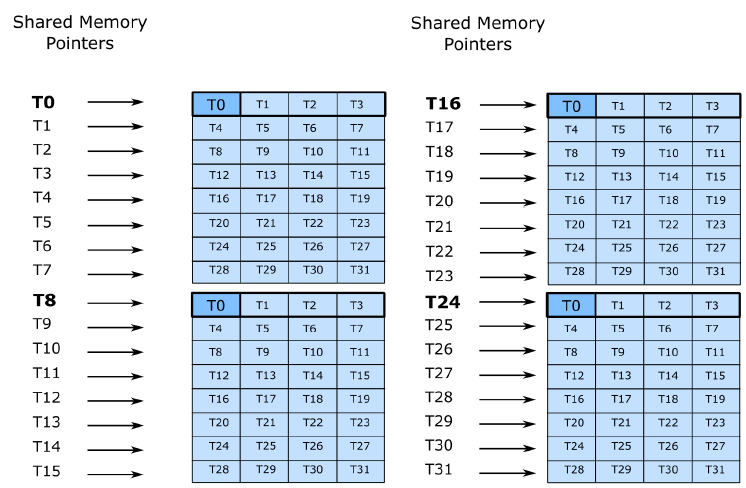
写完之后如下，每个格子为16B，即8个FP16，Ti为线程id，和global mem中对应，这个过程中不会bank冲突
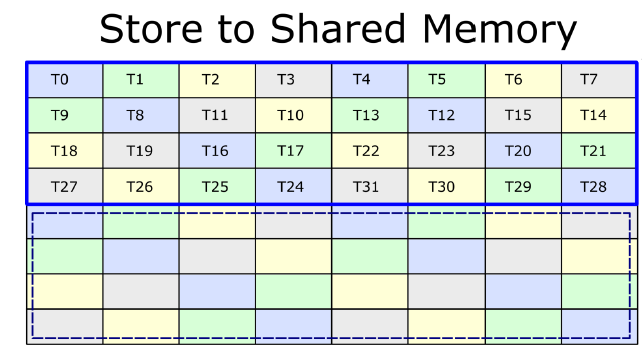
在这里插入图片描述

图 3-2
## Q乘K 然后再回看内循环流程，gemm_q_k负责第一个矩阵运算，即QK，这里会load Q和K。 
inline __device__ void device_1xN_(const Params &params, const int bidb, const int bidh, int steps, Prng &ph, const int loop_step_idx) {
    ...
    gemm_q_k.load_q();

    // Load the fragments for V. We keep the data in registers during the entire kernel.
    typename Smem_tile_v::Fragment frag_v[Mma_tile_o::MMAS_K][Mma_tile_o::MMAS_N];
    #pragma unroll
    for( int ki = 0; ki < Mma_tile_o::MMAS_K; ++ki ) {
        smem_v.load(frag_v[ki], ki);
    }

    // Commit the data for V to shared memory if it has not been done already.
    if( Kernel_traits::SHARE_SMEM_FOR_K_AND_V ) {
        // Make sure we are done loading the fragments for K.
        __syncthreads();

        // Commit the data to shared memory for V.
        gmem_k.commit(gemm_q_k.smem_k);

        // Make sure the data is in shared memory.
        __syncthreads();
    }

    // Load the fragments for K. 
    gemm_q_k.load_k();
    ...
}

实就是通过ldmatrix指令将数据从shared mem中load到寄存器中，首先看下Gemm_Q_K的继承关系，成员就是Fragment和两个Smem_tile，Fragment的核心成员就是多个32位寄存器变量。

template<typename Kernel_traits>
struct Gemm_Q_K_base {
    using Smem_tile_o = typename Kernel_traits::Smem_tile_o;
    using Smem_tile_q = typename Kernel_traits::Smem_tile_q;
    using Smem_tile_k = typename Kernel_traits::Smem_tile_k;
    using Fragment_q = typename Smem_tile_q::Fragment;
    using Fragment_k = typename Smem_tile_k::Fragment;

    // The description of the CTA tile for the 1st batched GEMM.
    using Cta_tile_p = typename Kernel_traits::Cta_tile_p;

    // The MMA tile for the 1st GEMM.
    using Mma_tile_p = fmha::Hmma_tile<Cta_tile_p>;

    static constexpr int SMEM_BYTES_SOFTMAX = Cta_tile_p::M * Cta_tile_p::WARPS_N * sizeof(float) * 2;

    __device__ inline Gemm_Q_K_base(char * smem_ptr_q, char * smem_ptr_k, const int tidx) 
        : smem_q(smem_ptr_q, tidx)
        , smem_k(smem_ptr_k, tidx) {

    }

    __device__ inline void load_q() {
        smem_q.load(frag_q[0], 0);
    }

    __device__ inline void reload_q() {
        smem_q.load(frag_q[0], 0);
    }

    Fragment_q frag_q[2][Mma_tile_p::MMAS_M];
    Smem_tile_q smem_q;
    Smem_tile_k smem_k;
};

template<typename Kernel_traits, bool K_in_regs, typename elem_type_=__half>
struct Gemm_Q_K : public Gemm_Q_K_base<Kernel_traits>

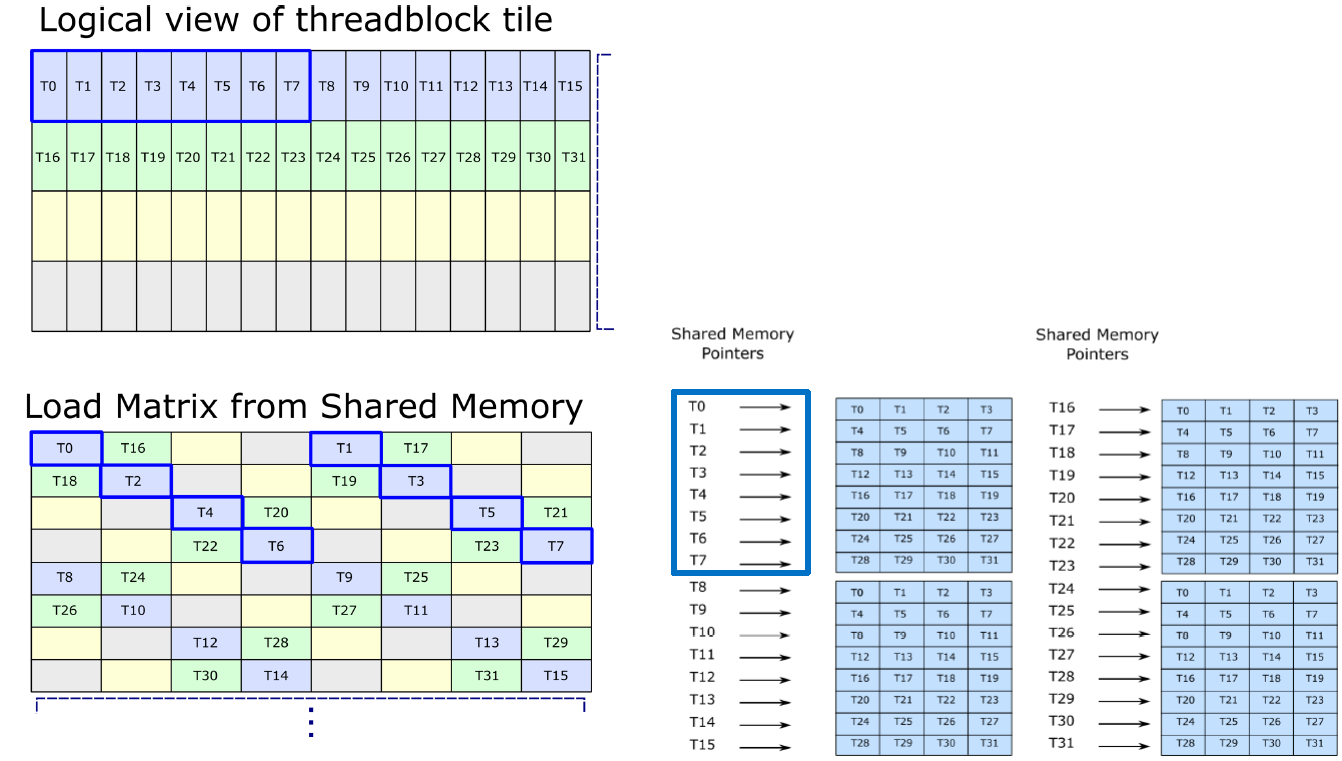
然后看下Smem_tile如何执行load，在构造函数中会计算出每个线程应该读哪行哪列，如图2-7

inline __device__ Smem_tile_row_a(void *smem, int tidx) : Base(smem, tidx) {
    const int WARPS_M = Cta_tile::WARPS_M;
    const int WARPS_N = Cta_tile::WARPS_N;
    const int WARPS_K = Cta_tile::WARPS_K;

    static_assert(WARPS_M == 1);
    static_assert(WARPS_N == 4 || WARPS_N == 8);
    static_assert(WARPS_K == 1);
    static_assert(Base::ROWS_PER_XOR_PATTERN == 2 || Base::ROWS_PER_XOR_PATTERN == 4 || Base::ROWS_PER_XOR_PATTERN == 8);

    // The row and column read by the thread.
    int smem_read_row  = (tidx & 0x0f);
    constexpr int ROWS_PER_PACKING = Base::BYTES_PER_ROW / Base::BYTES_PER_ROW_BEFORE_PACKING;                              // 2
    int smem_read_col = ((smem_read_row / ROWS_PER_PACKING) % Base::ROWS_PER_XOR_PATTERN) * Base::COLS_PER_XOR_PATTERN;
    smem_read_col ^= (tidx & 0x10) / 16;

    // The shared memory offset.
    this->smem_read_offset_ = smem_read_row*Base::BYTES_PER_ROW_BEFORE_PACKING + smem_read_col*BYTES_PER_LDS;
}

然后执行load，通过ldmatrix将数据从shared mem load到了寄存器，执行结束之后，寄存器变量和原始矩阵关系如图2-5，load结束后会计算smem_read_offset，指向下一个16x16矩阵，即k维度上边的下一个矩阵。

inline __device__ void load(Fragment (&a)[Mma_tile::MMAS_M], int ki) {
    #pragma unroll
    for( int mi = 0; mi < Mma_tile::MMAS_M; ++mi ) {
        // Jump by as many matrix rows as needed (a row in smem may pack multiple matrix rows).
        int offset = mi * Mma_tile::M_PER_MMA_PER_CTA * Base::BYTES_PER_ROW_BEFORE_PACKING;

        // Load using LDSM.M88.4.
        uint4 tmp;
        // ldsm(tmp, this->smem_ + this->smem_read_offset_ + this->smem_read_buffer_ + offset);
        ldsm(tmp, this->smem_ + this->smem_read_offset_ + offset);

        // Store the value into the fragment.
        a[mi].reg(0) = tmp.x;
        a[mi].reg(1) = tmp.y;
        a[mi].reg(2) = tmp.z;
        a[mi].reg(3) = tmp.w;
    }

    // Move the offset to the next possition. See doc/mma_smem_layout.xlsx.
    static_assert(Mma_tile_with_padding::MMAS_K < 64, "Not implemented");
    if(        Mma_tile_with_padding::MMAS_K >= 32 && ki % 16 == 15 ) {
        this->smem_read_offset_ ^= 31 * BYTES_PER_LDS * 2;
    } else if( Mma_tile_with_padding::MMAS_K >= 16 && ki %  8 ==  7 ) {
        this->smem_read_offset_ ^= 15 * BYTES_PER_LDS * 2;
    } else if( Mma_tile_with_padding::MMAS_K >=  8 && ki %  4 ==  3 ) {
        this->smem_read_offset_ ^=  7 * BYTES_PER_LDS * 2;
    } else if( Mma_tile_with_padding::MMAS_K >=  4 && ki %  2 ==  1 ) {
        this->smem_read_offset_ ^=  3 * BYTES_PER_LDS * 2;
    } else if( Mma_tile_with_padding::MMAS_K >=  2 ) {
        this->smem_read_offset_ ^=  1 * BYTES_PER_LDS * 2;
    }
}

然后执行矩阵运算，注意这里做了访存和计算的流水线，先load下一个矩阵，再执行当前的计算，结果存到Fragment acc_p的寄存器中。

template<typename Acc, int M, int N>
    __device__ inline void operator()(Acc (&acc_p)[M][N]){
        // Do this part of P^T = (Q * K^T)^T.
        #pragma unroll
        for( int ki = 1; ki < Mma_tile_p::MMAS_K; ++ki ) {
            // Trigger the load from shared memory for the next series of Q values.
            Base::smem_q.load(Base::frag_q[ki & 1], ki);
            // Do the math for the values already in registers.
            fmha::gemm_cl<elem_type>(acc_p, Base::frag_q[(ki - 1) & 1], frag_k[(ki - 1)]);
        }
        // Do the final stage of math.
        {
            int ki = Mma_tile_p::MMAS_K;
            fmha::gemm_cl<elem_type>(acc_p, Base::frag_q[(ki - 1) & 1], frag_k[(ki - 1)]);
        }
    }

这里gemm_cl用了cutlass，我们直接看下原始apex的逻辑，其实就是对每个16x16的tile执行mma函数，mma函数中会执行两次16x8x16的mma.sync

template<typename Acc, typename A, typename B, int M, int N>
inline __device__ void gemm(Acc (&acc)[M][N], const A (&a)[M], const B (&b)[N]) {

    #pragma unroll
    for( int mi = 0; mi < M; ++mi ) {
        #pragma unroll
        for( int ni = 0; ni < N; ++ni ) {
            acc[mi][ni].mma(a[mi], b[ni]);
        }
    }
}

template< typename Layout_a, typename Layout_b >
inline __device__ void mma(const Fragment_a<Layout_a> &a,
                           const Fragment_b<Layout_b> &b) {
    asm volatile( \
        "mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32 \n" \
        "    {%0, %1, %2, %3}, \n" \
        "    {%4, %5, %6, %7}, \n" \
        "    {%8, %9}, \n" \
        "    {%0, %1, %2, %3}; \n" \
                : "+f"(  elt(0)), "+f"(  elt(1)), "+f"(  elt(2)), "+f"(  elt(3))
                :  "r"(a.reg(0)),  "r"(a.reg(1)),  "r"(a.reg(2)),  "r"(a.reg(3))
                ,  "r"(b.reg(0)),  "r"(b.reg(1)));
    asm volatile( \
        "mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32 \n" \
        "    {%0, %1, %2, %3}, \n" \
        "    {%4, %5, %6, %7}, \n" \
        "    {%8, %9}, \n" \
        "    {%0, %1, %2, %3}; \n" \
                : "+f"(  elt(4)), "+f"(  elt(5)), "+f"(  elt(6)), "+f"(  elt(7))
                :  "r"(a.reg(0)),  "r"(a.reg(1)),  "r"(a.reg(2)),  "r"(a.reg(3))
                ,  "r"(b.reg(2)),  "r"(b.reg(3)));
}

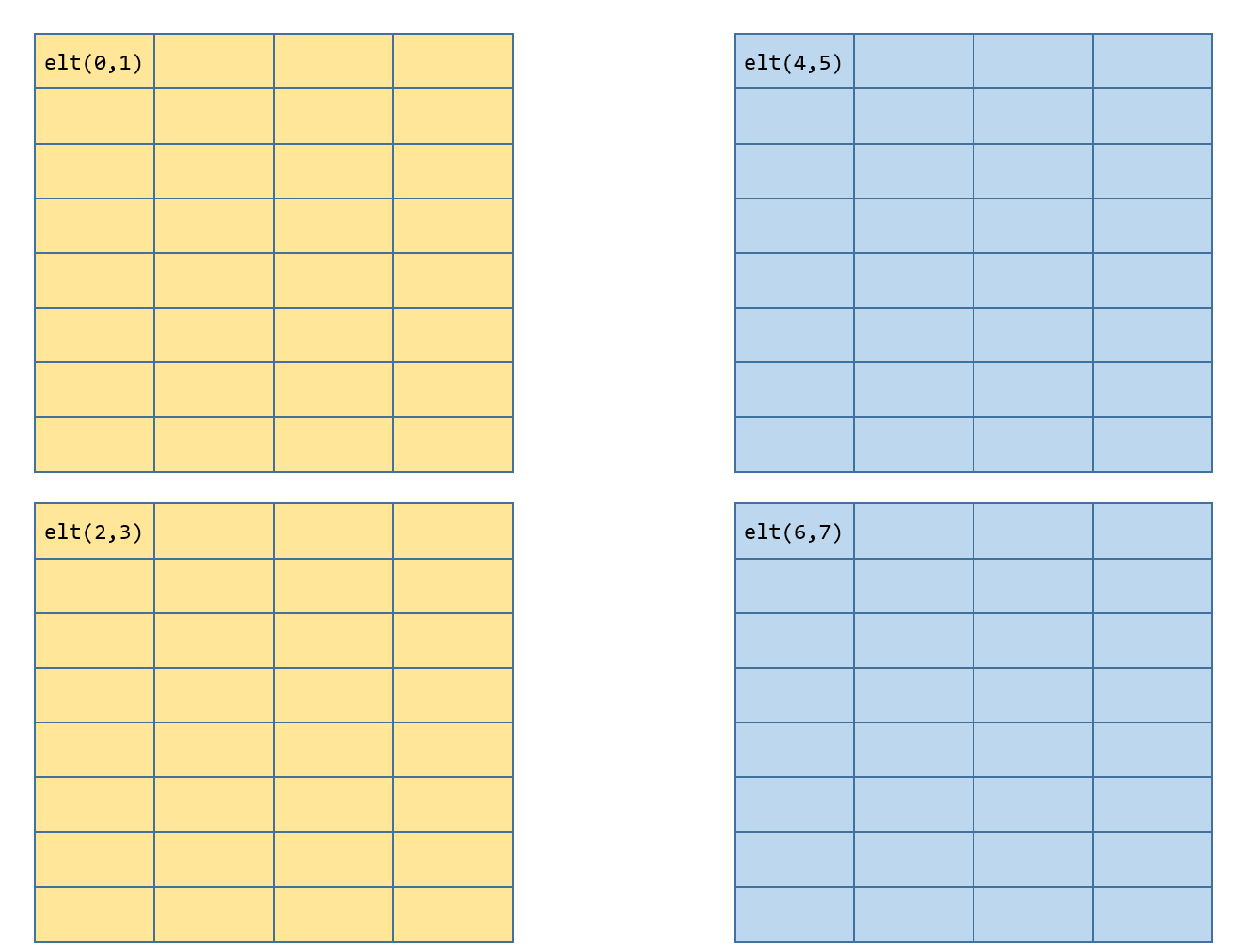
对于第一个线程的第一个acc_p的第一个Fragment，寄存器和结果矩阵对应关系如下，黄色为第一个16x8，蓝色为第二个16x8
在这里插入图片描述

图 3-3
cta中warp的组织格式为m1n4k1，Q矩阵为16x32，K矩阵为32x128，warp排布如下，图3-3对应图3-4 warp0的第一个16x16的计算结果w01

在这里插入图片描述

图 3-4
到现在就完成了QK的计算 ## softmax 接下来要计算max，看下Softmax这个类，核心数据结构如下，其中elt_是存储acc_p的输出，Smem_tile_red为共享内存，用于计算P的max和sum 
template<typename Cta_tile, typename Kernel_traits>
struct Softmax_base {
    ...
    
    float elt_[MMAS_M * 2][MMAS_N * 4];
};

template<typename Cta_tile, typename Kernel_traits>
struct Softmax : public Softmax_base<Cta_tile, Kernel_traits> {

    Smem_tile_red smem_max_;
    Smem_tile_red smem_sum_;
};

然后继续看下内循环

template<typename Kernel_traits, bool Is_dropout, bool Is_causal, bool Return_softmax, typename Params>
inline __device__ void device_1xN_loop(const Params &params) {
    ...
    
    softmax.unpack_noscale(acc_p);
    float p_max[Mma_tile_p::MMAS_M * 2];
    softmax.template reduce_max</*zero_init=*/Is_first>(p_max);
    
    ...
 }

首先通过unpack_noscale将数据从acc_p中存到Softmax的elt_。

inline __device__ void unpack_noscale(const Accumulator (&acc)[MMAS_M][MMAS_N]) {

    #pragma unroll
    for( int mi = 0; mi < MMAS_M; ++mi ) {
        #pragma unroll
        for( int ni = 0; ni < MMAS_N; ++ni ) {
            // 1st row - 4 elements per row.
            this->elt_[2 * mi + 0][4 * ni + 0] = acc[mi][ni].elt(0);
            this->elt_[2 * mi + 0][4 * ni + 1] = acc[mi][ni].elt(1);
            this->elt_[2 * mi + 0][4 * ni + 2] = acc[mi][ni].elt(4);
            this->elt_[2 * mi + 0][4 * ni + 3] = acc[mi][ni].elt(5);
            // 2nd row - 4 elements per row.
            this->elt_[2 * mi + 1][4 * ni + 0] = acc[mi][ni].elt(2);
            this->elt_[2 * mi + 1][4 * ni + 1] = acc[mi][ni].elt(3);
            this->elt_[2 * mi + 1][4 * ni + 2] = acc[mi][ni].elt(6);
            this->elt_[2 * mi + 1][4 * ni + 3] = acc[mi][ni].elt(7);
        }
    }
}

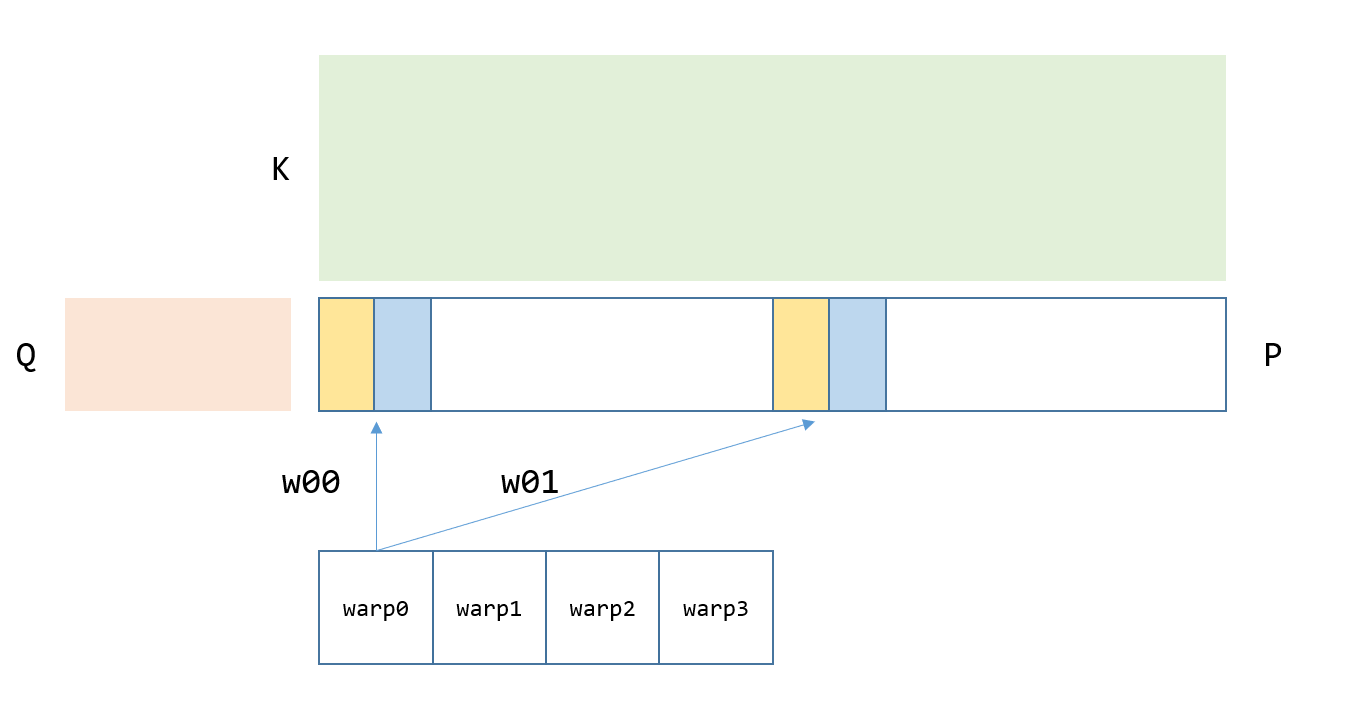
w00 unpack之后的数据在softmax中分布如图3-4左侧k = 0,1,2,3，w01 unpack之后如图3-4右侧k = 4,5,6,7
在这里插入图片描述

图 3-5
然后看下求max的过程，后续求sum过程一致，就不再赘述了。 
template<bool zero_init=true, typename Operator>
__device__ inline void reduce_(float (&frag)[2 * MMAS_M], Operator &op, Smem_tile_red & smem_red) {
    thread_reduce_<zero_init>(frag, op);
    quad_reduce(frag, frag, op);
    smem_red.store(frag);
    __syncthreads();
    typename Smem_tile_red::read_t tmp[2 * MMAS_M];
    smem_red.load(tmp);
    quad_allreduce(frag, tmp, op);
}

第一步为执行thread_reduce，就是将单个线程内同一行的做一次reduce，对于图3-4，m=0,2的8个float会执行一次reduce得到个最大值存到p_max[0]，m=2,3的8个float会执行一次reduce得到个最大值存到p_max[1]

template<bool zero_init=true, typename Operator>
__device__ inline void thread_reduce_(float (&frag)[2 * MMAS_M], Operator &op) {
    #pragma unroll
    for( int mi = 0; mi < 2 * MMAS_M; mi++ ) {
        frag[mi] = zero_init ? this->elt_[mi][0] : op(frag[mi], this->elt_[mi][0]);
        #pragma unroll
        for( int ni = 1; ni < 4 * MMAS_N; ni++ ) {
            frag[mi] = op(frag[mi], this->elt_[mi][ni]);
        }
    }
}

第二步执行warp内同一行的reduce，T0-3一行，T4-7一行，因此要执行quad之间的reduce，这里使用warp shuffle来做的，经过第一次shuffle之后T0 = max(T0, T2)，T1 = max(T1, T3)，经过第二次shuffle之后T0就拿到了当前warp当前行(即第0行)的最大值

template<typename Operator, int M>
__device__ inline void  quad_reduce(float (&dst)[M], float (&src)[M], Operator &op) {
    #pragma unroll
    for(int mi=0; mi < M; mi++){
        dst[mi] = src[mi];
        dst[mi] = op(dst[mi], __shfl_down_sync(uint32_t(-1), dst[mi], 2));
        dst[mi] = op(dst[mi], __shfl_down_sync(uint32_t(-1), dst[mi], 1));
    }
}

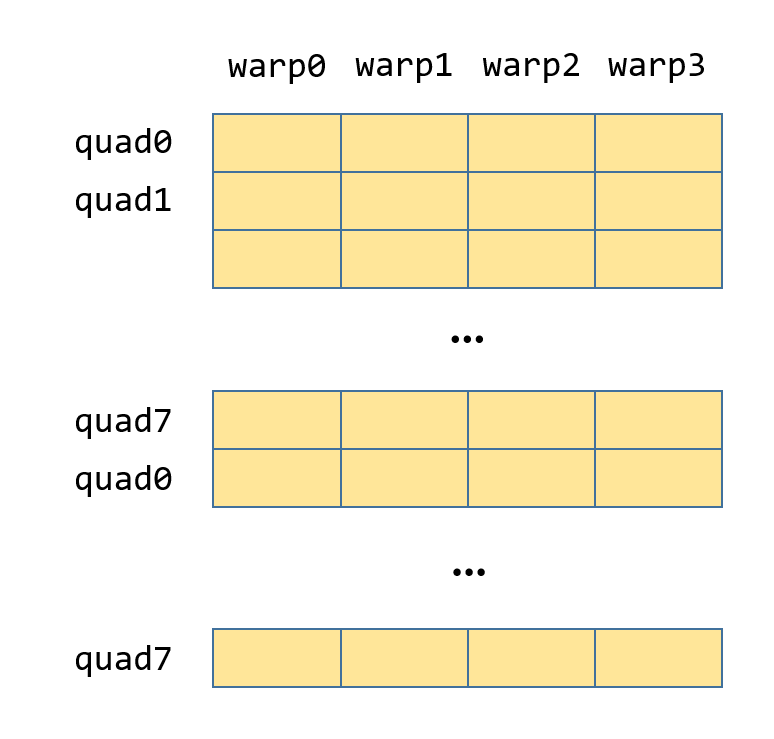
第三步会将warp内的每行的最大值写入到shared mem，只有每个quad的第0个线程会写，写完之后如图3-5
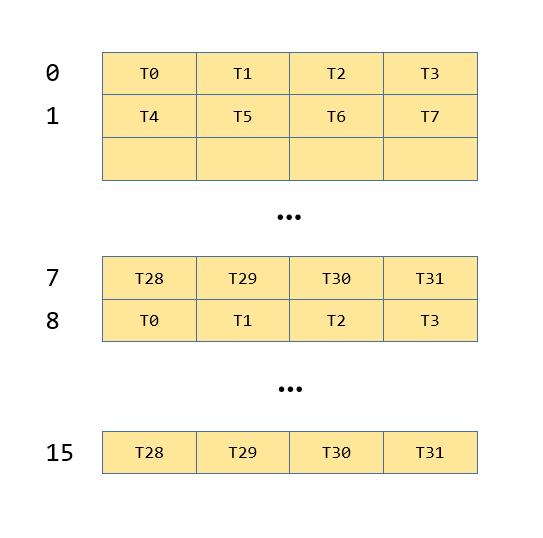
在这里插入图片描述

图 3-6
第四步所有warp都会按照图3-6的数据线程排布将数据从share mem中load出来，这样每个线程就拿到了当前行其他warp的数值

在这里插入图片描述

图 3-7
第五步执行quad_allreduce，也是通过warp shuffle做的，以quad0为例，第一次T0 = T2 = max(T0, T2)，T1 = T3 = max(T1, T3)，第二次T0 = T1 = max(T0, T1)，T2 = T3 = max(T2, T3)，这样每个线程就都拿到了当前行的最大值。 
template<typename Operator, int M>
__device__ inline void quad_allreduce(float (&dst)[M], float (&src)[M], Operator &op) {
    #pragma unroll
    for(int mi=0; mi < M; mi++){
        dst[mi] = src[mi];
        dst[mi] = Allreduce<4>::run(dst[mi], op);
    }
}
template<int THREADS>
struct Allreduce {
    static_assert(THREADS == 32 || THREADS == 16 || THREADS == 8 || THREADS == 4);
    template<typename T, typename Operator>
    static __device__ inline T run(T x, Operator &op) {
        constexpr int OFFSET = THREADS / 2;
        x = op(x, __shfl_xor_sync(uint32_t(-1), x, OFFSET));
        return Allreduce<OFFSET>::run(x, op);
    }
};

template<>
struct Allreduce<2> {
template<typename T, typename Operator> 
static __device__ inline T run(T x, Operator &op) {
    x = op(x, __shfl_xor_sync(uint32_t(-1), x, 1));                 
    return x;
}

到这里，最大值就计算出来存到p_max中了。

然后根据max计算exp

softmax.scale_apply_exp(p_max, params.scale_bmm1f);

然后计算sum，这里sum整体流程和求max完全一致，不过只执行到第三步，即将quad reduce的结果写回到shared mem，原因后续会提到

float p_sum[Mma_tile_p::MMAS_M * 2];
softmax.reduce_sum_before_sync_(p_sum);

然后将softmax的结果，并将softmax的FP32转为FP16存到frag_p中

using Frag_p = fmha::Fragment_a<fmha::Row>;
Frag_p frag_p[Mma_tile_o::MMAS_K][Mma_tile_o::MMAS_M];
softmax.template pack<elem_type>(frag_p);

P乘V

然后开始算PxV，P的shape为[16, 128]，V的shape为[128, 32]，对于QxK的warp是在M维度分块，PxV的分块在K维度，具体分块逻辑如图3-7，黄色部分为warp0负责计算。
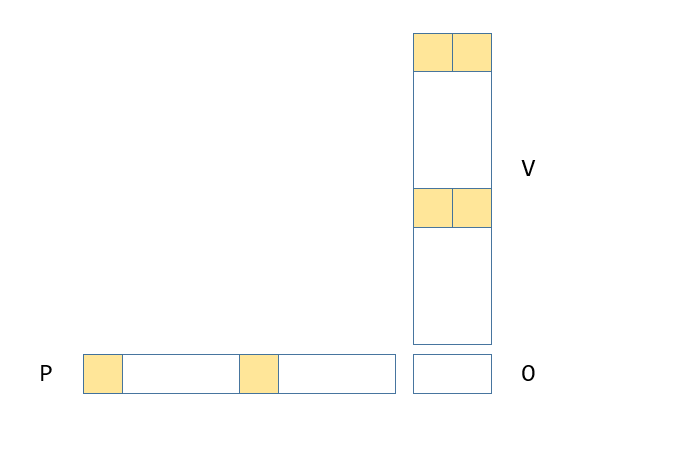
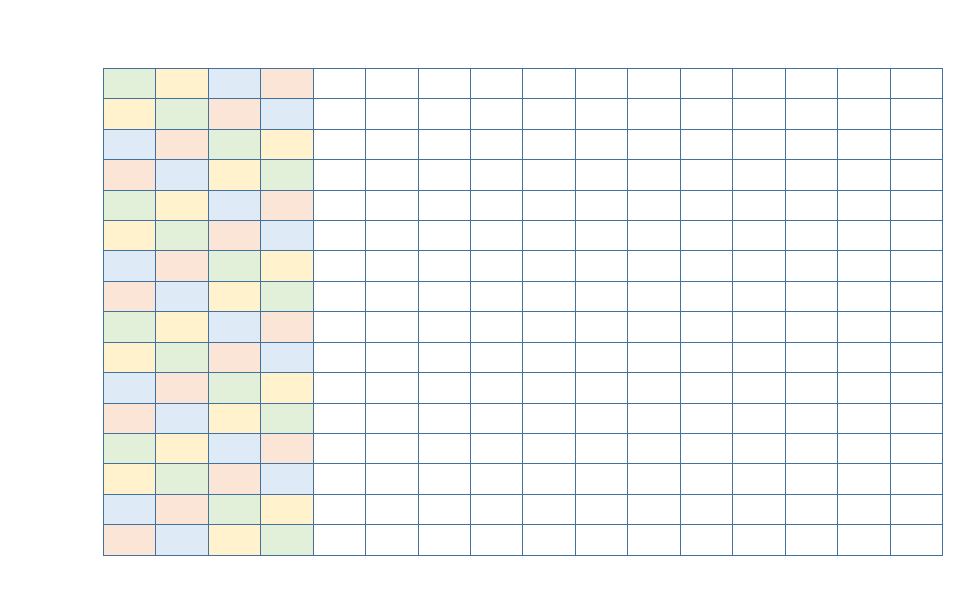
在这里插入图片描述

图 3-8
不过这里每个warp都有一个O矩阵，还需要将warp间的O进行reduce，这里对O的的线程分块和P不一致，因此之前在求sum的时候只执行到了第三步，原因就是线程对应的数据分块变了。具体的，这里用于reduce的share mem大小为16x128，每个warp将自己的16x32结果存到share mem的32列，如图3-8，颜色区域为第一个warp写入的。

在这里插入图片描述

图 3-9
然后再load出去，每个线程load 4行，一行8个线程，load的过程中执行reduce。除以sum之后就完成了第一次O的计算，写回global mem。 ## 递推过程 重复内循环直到完成第一次外循环，第一次外循环的计算流程本质和朴素算法一致，然后看下之后的外循环是如何完成递推的。 第一次外循环中会将中间变量写到global mem，比如o_tmp，就是O的中间结果，还保存了gmem_softmax_lse，代表max + log(sum) 
for (int jj = 0; jj < Gmem_tile_o::STGS_PER_LOOP; jj++) {
    float sum = p_sum_o[jj][0];
    p_sum_log[jj][0] = (sum == 0.f || sum != sum) ? -INFINITY : p_max_o[jj][0] + __logf(sum);
  
    if (tidx % Gmem_tile_o::THREADS_PER_ROW == 0) {
        gmem_softmax_lse.store_row(
            reinterpret_cast<uint32_t(&)[Mma_tile_p::MMAS_M]>(p_sum_log[jj]), rows[jj]);
    }
}

之后的外循环会先计算max，不过new_max = max(prev_lse, cur_max)，这里是为了实现方便，只保存lse，而不需要保存max，效果上是等价的，new_max一定大于max。

float p_max[Mma_tile_p::MMAS_M * 2];
if (!Is_first) {
    smem_softmax_lse.store_pair(p_prev_lse);
   
    for (int mi = 0; mi < Mma_tile_p::MMAS_M * 2; mi++) { p_max[mi] = p_prev_lse[mi] / params.scale_bmm1f; }
}
softmax.template reduce_max</*zero_init=*/Is_first>(p_max);

然后计算p_prev_scale_o，即 ( e m i − m i n e w ) l i (e^{m_i - m^{new}_i}) l_i (emi​−minew​)li​，和p_sum_o，即 l i n e w l^{new}_i linew​，由于p_sum_o计算过程中使用的是new_max，所以不需要对p_sum_o进行修正。

for (int jj = 0; jj < Gmem_tile_o::STGS_PER_LOOP; jj++) {
    p_prev_scale_o[jj] = expf(p_prev_scale_o[jj] - p_max_o[jj][0]);
    p_sum_o[jj][0] += p_prev_scale_o[jj];
}

然后计算
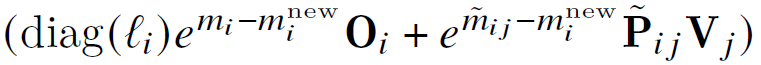
在这里插入图片描述

uint4 out[Gmem_tile_o::STGS_PER_LOOP];
if (!Is_first) { gmem_o_tmp.load(out, 0); }
...
if (!Is_first) {
    for (int jj = 0; jj < Gmem_tile_o::STGS_PER_LOOP; jj++) {
        out[jj] = fmha::fmul4(out[jj], p_prev_scale_o[jj]);
    }
}

学习过程中和lw911014讨论了很多，非常感谢