机器学习算法基础--KNN分类算法
1.KNN算法原理介绍
KNN(K-Nearest Neighbor)工作原理:
在一个存在标签的数据集中,当我们输入一个新的没有标签的样本时候,KNN算法的任务就是将该样本分类,即给定其对应的样本标签。
输入没有标签的数据后,将新数据中的每个特征与样本集中数据对应的特征进行比较,提取出样本集中特征最相似数据(最近邻)的分类标签。
一般来说我们选取的是新样本的最近的k个样本进行"投票"决策,这就是KNN算法中k的意思,
通常k是不大于20的整数。最后选择k个最相似数据中出现次数最多的分类作为新数据的分类。
2.KNN分类决策原则
KNN算法一般是用多数表决方法,即由输入实例的K个邻近的多数类决定输入实例的类。这种思想也是经验风险最小化的结果。
训练样本为
(
x
i
,
y
i
)
(x_{i} ,y_{i})
(xi,yi)。当输入实例为 x,标记为c,
N
k
(
x
)
N_{_k}(x)
Nk(x)是输入实例x的k近邻训练样本集。我们定义训练误差率是K近邻训练样本标记与输入标记不一致的比例,误差率表示为:
1
k
∑
x
i
∈
N
k
(
x
)
I
(
y
i
≠
c
j
)
=
1
−
1
k
∑
x
i
∈
N
k
(
x
)
I
(
y
i
=
c
j
)
\frac1k\sum_{x_i\in N_{k}(x)}I(y_i\neq c_j)=1-\frac1k\sum_{x_i\in N_{k}(x)}I(y_i=c_j)\quad
k1xi∈Nk(x)∑I(yi=cj)=1−k1xi∈Nk(x)∑I(yi=cj)
因此,要使误差率最小化即经验风险最小,就要使
1
k
∑
x
i
∈
N
k
(
x
)
I
(
y
i
=
c
j
)
\frac{1}{k}\sum_{x_{i}\in N_{k}(x)}I(y_{i}=c_{j})
k1∑xi∈Nk(x)I(yi=cj)尽可能大,即K近邻的标记值尽可能的与输入标记一致,所以多数表决规则等价于经验风险最小化。
3.KNN度量距离介绍
3.1.闵可夫斯基距离
闵可夫斯基距离表示如下所示:
D
(
x
,
y
)
=
∣
x
1
−
y
1
∣
p
+
∣
x
2
−
y
2
∣
p
+
.
.
.
+
∣
x
n
−
y
n
∣
p
p
=
∑
i
=
1
n
∣
x
i
−
y
i
∣
p
p
\begin{aligned} D(x,y)& =\sqrt[p]{\mid x_1-y_1\mid^p+\mid x_2-y_2\mid^p+...+\mid x_n-y_n\mid^p} \\ &=\sqrt[p]{\sum_{i=1}^{n}\mid x_{i}-y_{i}\mid^{p}} \end{aligned}
D(x,y)=p∣x1−y1∣p+∣x2−y2∣p+...+∣xn−yn∣p=pi=1∑n∣xi−yi∣p
3.2.曼哈顿距离
曼哈顿距离如下所示:
D
(
x
,
y
)
=
∣
x
1
−
y
1
∣
+
∣
x
2
−
y
2
∣
+
.
.
.
.
+
∣
x
n
−
y
n
∣
=
∑
i
=
1
n
∣
x
i
−
y
i
∣
\begin{aligned} D(x,y)& =\mid x_1-y_1\mid+\mid x_2-y_2\mid+....+\mid x_n-y_n\mid \\ &=\sum_{i=1}^{n}\mid x_{i}-y_{i}\mid \end{aligned}
D(x,y)=∣x1−y1∣+∣x2−y2∣+....+∣xn−yn∣=i=1∑n∣xi−yi∣
3.3.欧式距离
欧式距离如下所示:
D
(
x
,
y
)
=
(
x
1
−
y
1
)
2
+
(
x
2
−
y
2
)
2
+
.
.
.
+
(
x
n
−
y
n
)
2
=
∑
i
=
1
n
(
x
i
−
y
i
)
2
\begin{aligned} D(x,y)& =\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+...+(x_n-y_n)^2} \\ &=\sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}} \end{aligned}
D(x,y)=(x1−y1)2+(x2−y2)2+...+(xn−yn)2=i=1∑n(xi−yi)2
4.KNN分类算法实现
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
#加载wine数据集
data = load_wine()
X = data.data[:, :2] #取前两列内容作为Alcohol和苹果酸作为样本
y = data.target
#划分数据集和测试集
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=42)
#创建KNN分类器,设置k=6
knn_classifier = KNeighborsClassifier(n_neighbors=10, metric='euclidean')#以欧式距离作为度量距离
knn_classifier.fit(X_train, y_train)
# 预测测试集
y_pred = knn_classifier.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
Accuracy: 0.8888888888888888
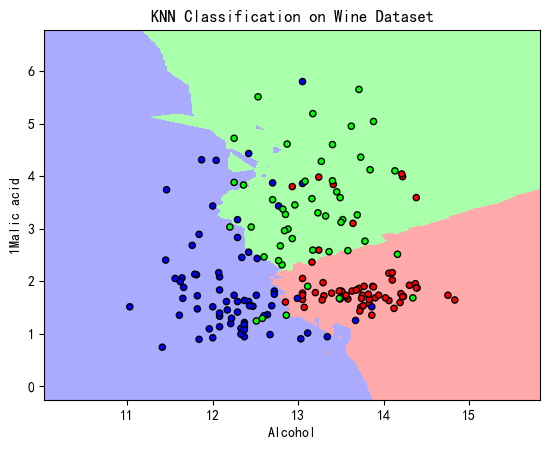
5.KNN分类算法效果
#可视化绘图
h = .02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# 获取预测结果
Z = knn_classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 创建颜色地图
cmap_background = ListedColormap(['#FFAAAA', '#AAAAFF', '#AAFFAA'])
cmap_points = ListedColormap(['#FF0000', '#0000FF', '#00FF00'])
# 可视化结果
plt.pcolormesh(xx, yy, Z, cmap=cmap_background)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_points,edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("KNN Classification on Wine Dataset")
plt.xlabel("Alcohol")
plt.ylabel("1Malic acid")
plt.show()
6.参考文章与致谢
本章内容的完成离不开大佬文章的启发和帮助,在这里列出名单,如果对于内容还有不懂的,可以移步对应的文章进行进一步的理解分析。
1.KNN算法:https://blog.csdn.net/qq_42722197/article/details/123196332?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169665324816800182743993%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169665324816800182743993&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-2-123196332-null-null.142^v95^chatgptT3_1&utm_term=knn%E7%AE%97%E6%B3%95%E5%8E%9F%E7%90%86&spm=1018.2226.3001.4187
如果大家这这篇blog中有什么不明白的可以去他的专栏里面看看,内容非常全面,应该能够有比较好的解答。
在文章的最后再次表达由衷的感谢!!