Java 数据结构与算法-队列
队列的基础知识
队列是一种常用的数据结构,它最大的特点是 “先入先出”……
在 Java 中,队列是一个定义了插入和删除操作的接口 Queue……
……在某些时候调用函数 add、remove 和 element 时可能会抛出异常,但调用函数 offer、poll 和 peek 不会抛出异常。例如,当调用函数 remove 从一个空的队列中删除最前面的元素时,就会抛出异常。但如果调用函数 poll 从一个空的队列中删除最前面的元素,则会返回 null
在 Java 中实现了接口 Queue 的常用类型有 LinkedList、ArrayDeque 和 PriorityQueue 等。但 PriorityQueue 并不是真正的队列,第 9 章会详细介绍 PriorityQueue
队列的应用
队列是一种经常被使用的数据结构。如果解决某个问题时数据的插入和删除操作满足 “先入先出” 的特点,那么考虑用队列来存储这些数据
面试题 41:滑动窗口的平均值
题目:请实现如下类型 MovingAverage,计算滑动窗口中所有数字的平均值,该类型构造函数的参数确定滑动窗口的大小,每次调用成员函数 next 时都会在滑动窗口中添加一个整数,并返回滑动窗口中所有数字的平均值
class MovingAverage {
private Queue<Integer> nums;
private int capacity;
private int sum;
public MovingAverage(int size) {
nums = new LinkedList<>();
capacity = size;
}
public double next(int val) {
nums.offer(val);
sum += val;
if (nums.size() > capacity) {
sum -= nums.poll();
}
return (double) sum / nums.size();
}
}
面试题 42:最近请求次数
题目:请实现如下类型 RecentCounter,它是统计过去 3000ms 内的请求次数的计数器。该类型的构造函数 RecentCounter 初始化计数器,请求数初始化为 0;函数 ping(int t) 在时间 t 添加一个新请求(t 表示以毫秒为单位的时间),并返回过去 3000ms 内(时间范围为 [t-3000, t])发生的所有请求数。假设每次调用函数 ping 的参数 t 都比之前调用的参数值大
class RecentCounter {
private Queue<Integer> times;
private int windowSize;
public RecentCounter() {
times = new LinkedList<>();
windowSize = 3000;
}
public int pint(int t) {
times.offer(t);
while (times.peek() + windowSize < t) {
times.poll();
}
return times.size();
}
}
每当请求 ping 在时间 t 发生时,时间 t 就被记录到队列 times 中。如果之前的某些请求的时间已经滑出了目前的时间窗口,则将它们从队列中删除。队列的长度就是当前时间窗口内请求的数目
假设计数器时间窗口的大小是 w 毫秒,其中记录的时间是递增的,那么时间窗口中记录的时间的数目是 O(w),因此空间复杂度是 O(w)。每当收到一个新的请求 ping 时,由于可能需要删除 O(w) 个已经滑出时间窗口的请求,因此时间复杂度也是 O(w)。但是由于题目中时间窗口的大小为 3000 毫秒,w 是一个常数,因此也可以认为时间复杂度和空间复杂度都是 O(1)
二叉树的广度优先搜索
应聘者在面试时经常需要使用队列来解决与广度优先搜索相关的问题。本节着重讨论二叉树的广度优先搜索,图的广度优先搜索在第 15 章介绍
……队列中最多需要存储一层的节点。在一棵满的二叉树中,最下面一层的节点数最多,最多可能有 (n+1)/2 个节点,因此,二叉树广度优先搜索的空间复杂度是 O(n)
由于队列的 “先入先出” 特性,二叉树的某一层节点按照从左到右的顺序插入队列中,因此这些节点一定会按照从左到右的顺序遍历到。如果用广度优先的顺序遍历二叉树,那么它的下一层节点也是从左到右的顺序添加到队列中的。因此,很容易知道每层最左边或最右边的节点,或者每层的最大值、最小值等。如果关于二叉树的面试题提到层这个概念,那么基本上可以确定该题目需要运用广度优先搜索
面试题 43:在完全二叉树中添加节点
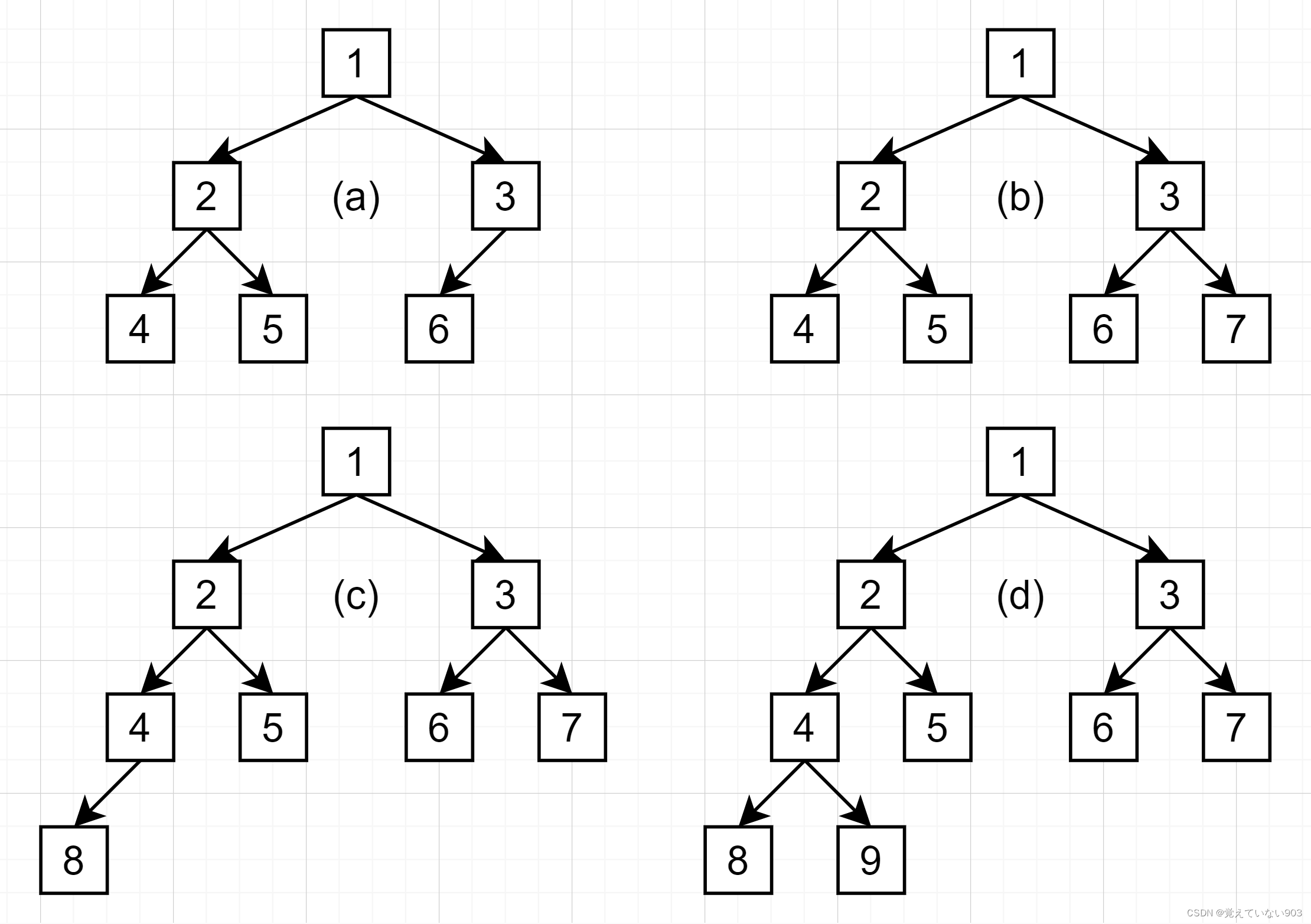
题目:在完全二叉树中,除最后一层之外其他层的节点都是满的(第 n 层有 2^(n-1) 个节点)。最后一层的节点可能不满,该层所有的节点尽可能向左边靠拢。例如,下图中的 4 棵二叉树均为完全二叉树。实现数据结构 CBTInserter 有如下 3 种方法
- 构造函数 CBTInserter(TreeNode root),用一棵完全二叉树的根节点初始化该数据结构
- 函数 insert(int v) 在完全二叉树中添加一个值为 v 的节点,并返回被插入节点的父节点
- 函数 get_root() 返回完全二叉树的根节点
class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
class CBTInserter {
private Queue<TreeNode> queue;
private TreeNode root;
public CBTInserter(TreeNode root) {
this.root = root;
queue = new LinkedList<>();
queue.offer(root);
while (queue.peek().left != null && queue.peek().right != null) {
TreeNode node = queue.poll();
queue.offer(node.left);
queue.offer(node.right);
}
}
public int insert(int v) {
TreeNode parent = queue.peek();
TreeNode node = new TreeNode(v);
if (parent.left == null) {
parent.left = node;
} else {
parent.right = node;
queue.poll();
queue.offer(parent.left);
queue.offer(parent.right);
}
return parent.val;
}
public TreeNode get_root() {
return this.root;
}
}
类型 CBTInserter 的构造函数按照广度优先搜索的顺序从根节点开始遍历输入的完全二叉树,如果一个节点的左右子节点都已经存在,就不可能再在这个节点添加新的子节点,因此可以从队列中删除这个节点,并将它的左右子节点都添加到队列之中……
最后分析上述代码的效率。类型 CBTInserter 的构造函数从本质上来说是按照广度优先搜索的顺序找出二叉树中所有既有左子节点又有右子节点的节点,因此时间复杂度是 O(n)。调用函数 insert 在完全二叉树中每添加一个节点最多只需要在队列中删除一个节点并添加两个节点。通常,队列的插入、删除操作的时间复杂度都是 O(1),因此函数 insert 的时间复杂度是 O(1)。显然,函数 get_root 的时间复杂度是 O(1)
类型 CBTInserter 需要一个队列来实现广度优先搜索算法保存缺少左子节点或右子节点的节点,空间复杂度是 O(n)
面试题 44:二叉树中每层的最大值
题目:输入一棵二叉树,请找出二叉树中每层的最大值
用一个队列实现二叉树的广度优先搜索
……可以用两个变量分别记录两层节点的数目,变量 current 记录当前遍历这一层中位于队列之中节点的数目,变量 next 记录下一层中位于队列之中节点的数目
最开始把根节点插入队列中时,把变量 current 初始化为 1……
当变量 current 的数值变成 0 时,表示当前层的所有节点都已经遍历完……
public static List<Integer> largestValues(TreeNode root) {
int current = 0;
int next = 0;
Queue<TreeNode> queue = new LinkedList<>();
if (root != null) {
queue.offer(root);
current = 1;
}
List<Integer> result = new LinkedList<>();
int max = Integer.MIN_VALUE;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
current--;
max = Math.max(max, node.val);
if (node.left != null) {
queue.offer(node.left);
next++;
}
if (node.right != null) {
queue.offer(node.right);
next++;
}
if (current == 0) {
result.add(max);
max = Integer.MIN_VALUE;
current = next;
next = 0;
}
}
return result;
}
用两个队列实现二叉树的广度优先搜索
另一个办法是把不同层的节点放入不同的队列中……
面试题 15:二叉树最低层最左边的值
题目:如何在一棵二叉树中找出它最底层最左边节点的值?假设二叉树中最少有一个节点
public static int findBottomLeftValue(TreeNode root) {
Queue<TreeNode> queue1 = new LinkedList<>();
Queue<TreeNode> queue2 = new LinkedList<>();
queue1.offer(root);
int bottomLeft = root.val;
while (!queue1.isEmpty()) {
TreeNode node = queue1.poll();
if (node.left != null) {
queue2.offer(node.left);
}
if (node.right != null) {
queue2.offer(node.right);
}
if (queue1.isEmpty()) {
queue1 = queue2;
queue2 = new LinkedList<>();
if (!queue1.isEmpty()) {
bottomLeft = queue1.peek().val;
}
}
}
return bottomLeft;
}
由于这个题目假设输入的二叉树至少有一个节点,因此根节点总是存在的。二叉树的第 1 层只有一个节点,即根节点,因此可以把变量 bottomLeft 初始化为根节点的值
接下来按照广度优先的顺序逐层遍历二叉树。当队列 queue1 被清空时,当前这一层都已经被遍历完,接下来可以开始下一层的遍历。如果下一层还有节点,则用下一层的第 1 个节点的值更新变量 bottomLeft。在整棵二叉树的遍历完成之后,变量 bottomLeft 的值就是最底层最左边节点的值
面试题 46:二叉树的右侧视图
题目:给定一棵二叉树,如果站在该二叉树的右侧,那么从上到下看到的节点构成二叉树的右侧视图。请写一个函数返回二叉树的右侧视图节点的值
public static List<Integer> rightSideView(TreeNode root) {
List<Integer> view = new LinkedList<>();
if (root == null) {
return view;
}
Queue<TreeNode> queue1 = new LinkedList<>();
Queue<TreeNode> queue2 = new LinkedList<>();
queue1.offer(root);
while (!queue1.isEmpty()) {
TreeNode node = queue1.poll();
if (node.left != null) {
queue2.offer(node.left);
}
if (node.right != null) {
queue2.offer(node.right);
}
if (queue1.isEmpty()) {
view.add(node.val);
queue1 = queue2;
queue2 = new LinkedList<>();
}
}
return view;
}
本章小结
本章介绍了队列这种数据结构。如果一个数据集合的添加、删除操作满足 “先入先出” 的特点,即最先添加的数据最先被删除,那么可以用队列来实现这个数据集合
队列经常被用来实现二叉树的广度优先搜索。首先将二叉树的根节点插入队列。然后每次从队列中取出一个节点遍历。如果该节点有子节点,则将该子节点插入队列。重复这个过程,直到队列被清空,此时二叉树所有的节点都已经遍历完
如果需要区分二叉树不同的层,那么至少有两种方法可以实现。第一种方法是用两个变量来表示当前层和下一层节点的数目。如果当前遍历的节点的数目变成 0,那么这一层所有的节点都已经遍历完,可以开始遍历下一层的节点。第二种方法是用两个队列分别存放当前层和下一层的节点。如果当前层对应的队列被清空,那么该层所有的节点就已经被遍历完,可以开始遍历下一层