信号与系统复习笔记

参考视频慕课《信号与线性系统分析》吴大正郭宝龙

1.1 信号的基本概念和分类

分类1
1.确定信号：可以用确定时间函数表示的信号
2.随机信号：不可以用确定函数表示，一般都是使用其统计特征进行研究

分类2 连续信号–离散信号

分类3 周期信号与非周期信号
在一定区间内，每隔一定时间T（整数N），按相同规律重复便的信号为周期信号，不满足条件的称为非周期信号

角频率的分类
模拟角频率Ω=2πf，过去我们常将ω作为模拟角频率，写成cos(ωt)，这种写法实际上是不正确的，应该写成cos(Ωt)来描述模拟余弦函数。此时Ω的取值也是从0到∞，这体现出模拟（角）频率没有周期性的特点。
数字角频率ω则是完全颠覆了我们过往对于频率的认识，首先要明确的是数字信号的获得是通过对模拟信号采样的方式。它的引入可以从cos(Ωt)开始。cos(Ωt)中相位变化一个周期(2π)所需的时间为T，那么模拟角频率定义成Ω=2π/T。对于该余弦信号，采样之后变成了一个离散的数字序列，此时再谈论过了多少时间走完一个周期已经没有意义，而是过了间隔N相位刚好变化一个周期。因此数字角频率推导出为ω=2π/N，余弦信号则为cos(ωn)。既然N是由对应一段时间T采样而来，那么N=T*Fs (Fs为采样率)，自然而然，ω=Ω/Fs。简单来说，数字角频率ω是模拟角频率Ω对于采样率Fs的归一化，这是数字角频率ω的核心要义

分类4 能量信号与功率信号
在这里插入图片描述

分类5 因果与反因果
信号发生之后都有信号，发生之前无信号为因果信号。反之为反因果信号

1.2 基本信号

信号与系统的3个基本问题
1、基本信号与基本响应
2、任意信号的分析
3、LTI系统的分析

1.2.1 阶跃函数

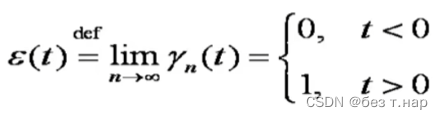
在这里插入图片描述
积分为斜坡函数

1.2.2 冲激函数

阶跃函数求导为冲激函数，冲激函数有取样特性
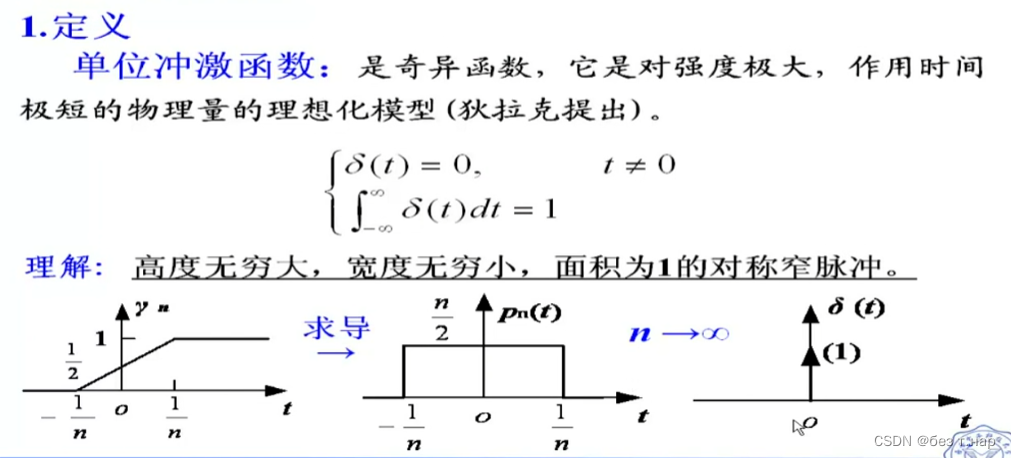
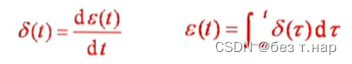
在这里插入图片描述

现实中可以用以下两种函数实现冲激函数的效果
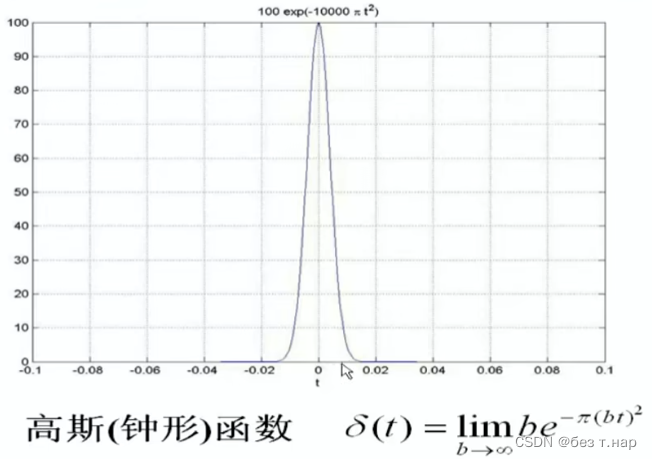
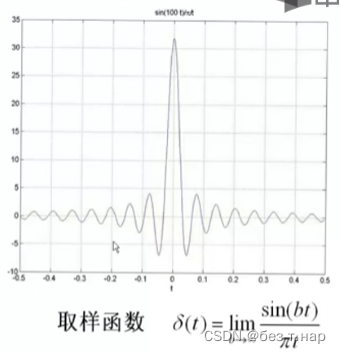
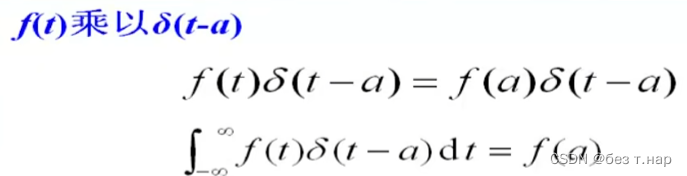
在这里插入图片描述

例如:

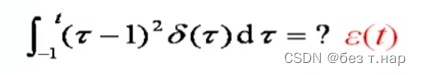
1.2.2.1 冲激偶

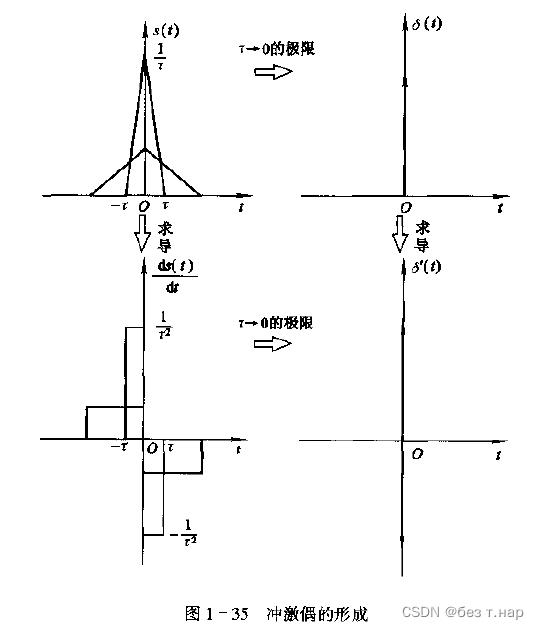
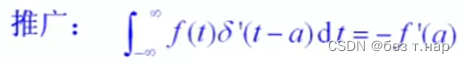
在这里插入图片描述

从冲激函数的一种定义方式去看，冲激偶呈现的是一种正负都有冲激的情况，冲激偶的积分自然是0；从奇偶函数去看，冲激函数为偶函数，导数自然为奇函数，奇函数在对称区间求积分为0.
冲激偶拓展到高阶
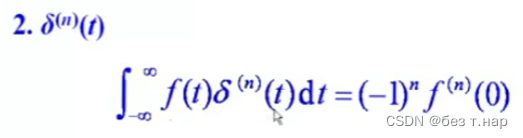
在这里插入图片描述

1.2.2.2 冲激函数的尺度变换

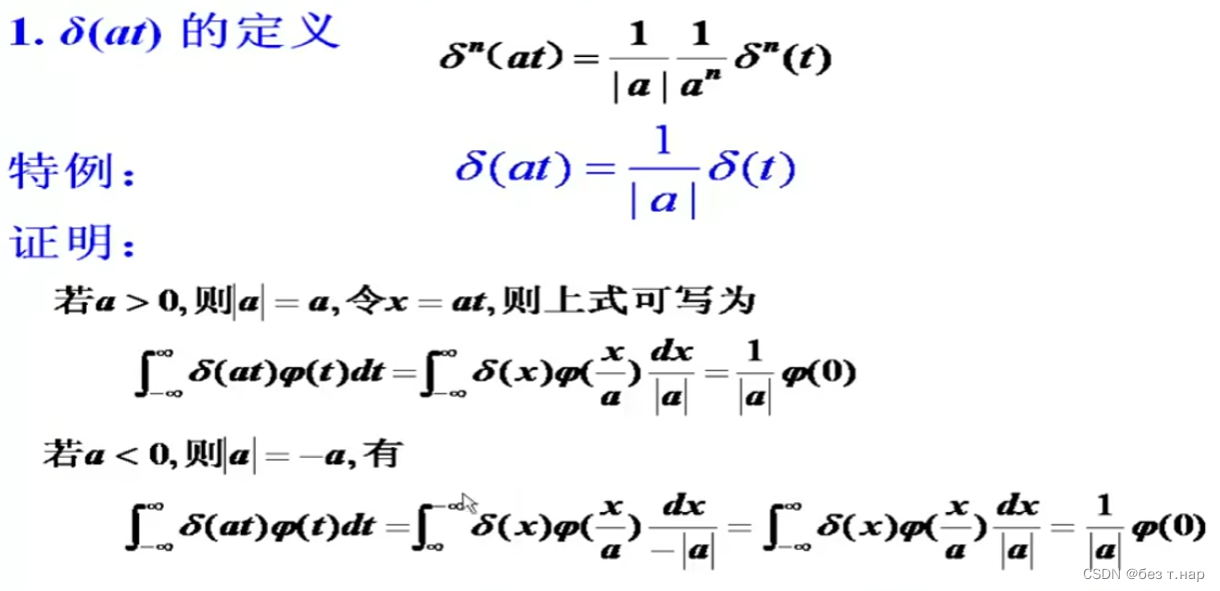
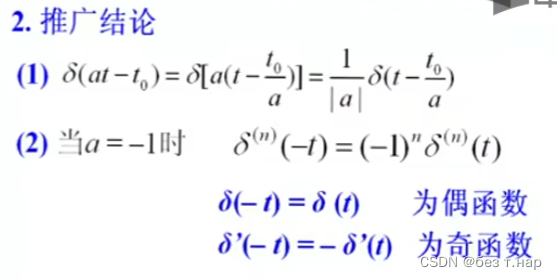
在这里插入图片描述

1.2.3 单位脉冲序列

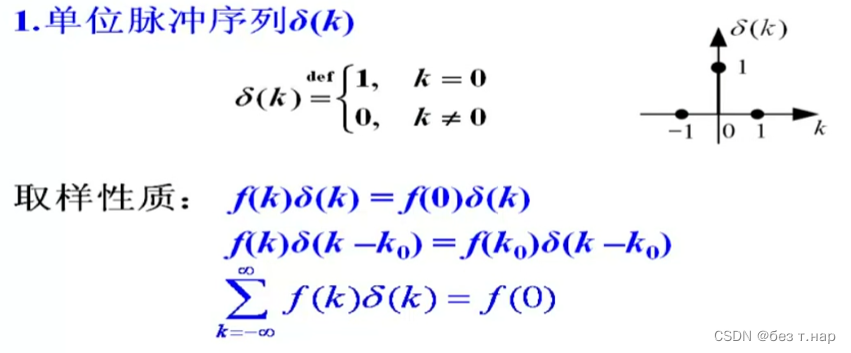
在这里插入图片描述

1.2.4 单位阶跃序列

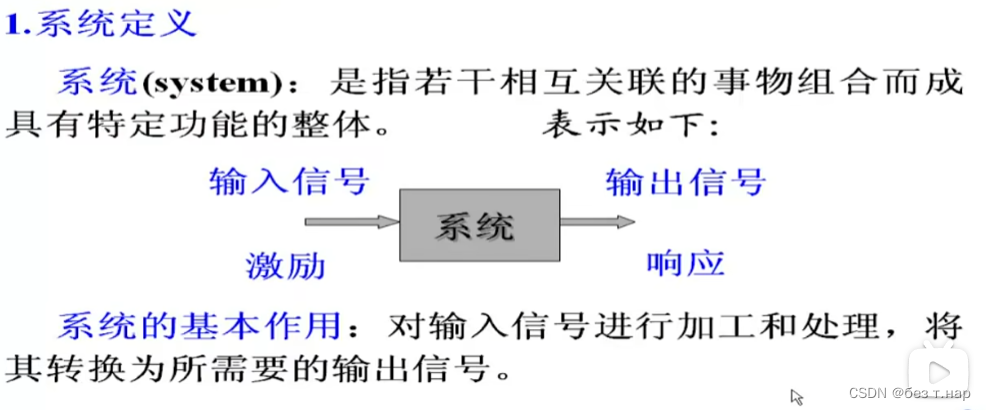
在这里插入图片描述

1.3 系统

在这里插入图片描述

状态：输出是由输入和系统状态（代表了系统过去的情况）决定的

1.3.1 线性系统与非线性系统

在这里插入图片描述

举例：

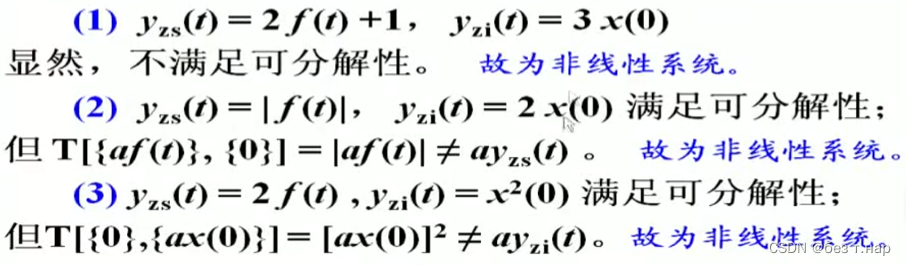
1.3.2 时变系统与时不变系统

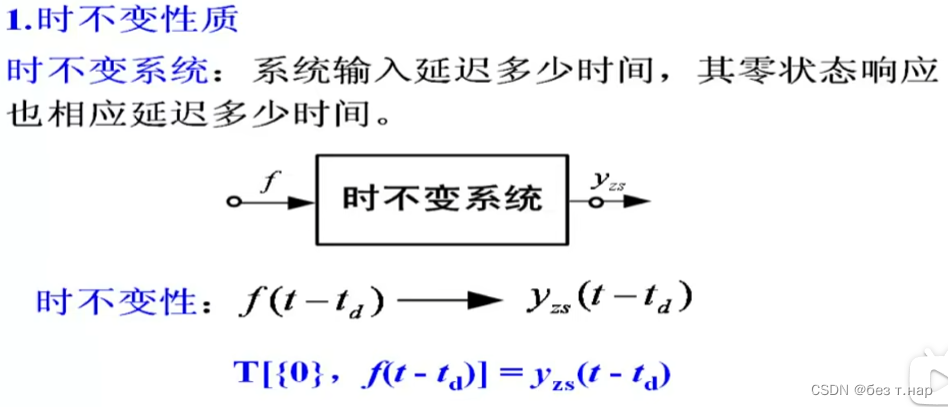
在这里插入图片描述
记住：输入延迟的情况与零状态响应一样才可以，先分开看在进行比较，输入输出关系中有变量的都是时变的。

1.3.3 LTI系统

在这里插入图片描述

1.3.4 因果与非因果系统

在这里插入图片描述
下面这个例题用到了线性时不变系统的基本性质

2.1 LTI连续系统的响应—微分方程的模拟框图

整个框图是不变的，但是根据输入输出的不同，中间的所写的函数可以变动，具体需要看输入输出
几个基本框图表示：积分器，数乘器，相加器
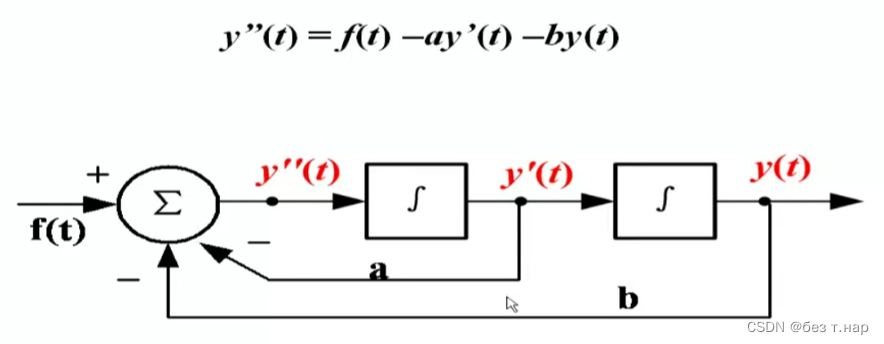
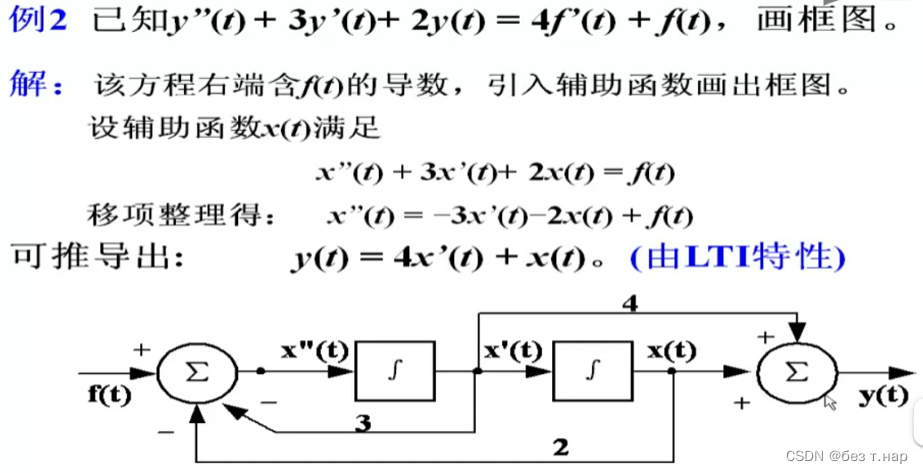
在这里插入图片描述

直接画整个系统的话框图中会出现3个积分器，系统是二阶的并不符合要求，所以用辅助函数去代替表达y(t)

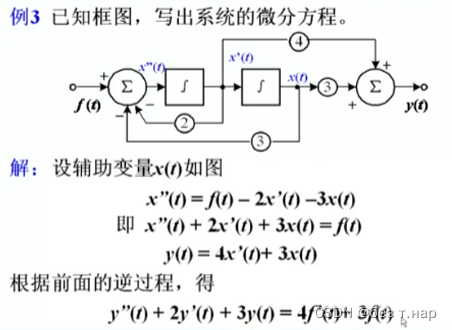
2.2 零输入与零状态响应

2.2.1 系统的初始值

需要根据初始值和初始状态求出响应
在这里插入图片描述
计算初始值时的一个基本原则，下面的结论是求初始的重要方式

2.2.2零输入响应-- yzi

系统零负时刻的值就是零状态响应的初值
解出是零输入响应仅在t>0时成立
在这里插入图片描述

2.2.3 零状态响应–yzs

在这里插入图片描述

求零状态响应时全响应公式即可转化为零状态的公式，这里的系统匹配发法是指两种响应分别匹配到不同阶数的导数上并且通过有无跳变去判断0前后的值，通过这样的方法去确定初始值

2.2.3 响应的分类

在这里插入图片描述

例子如下：

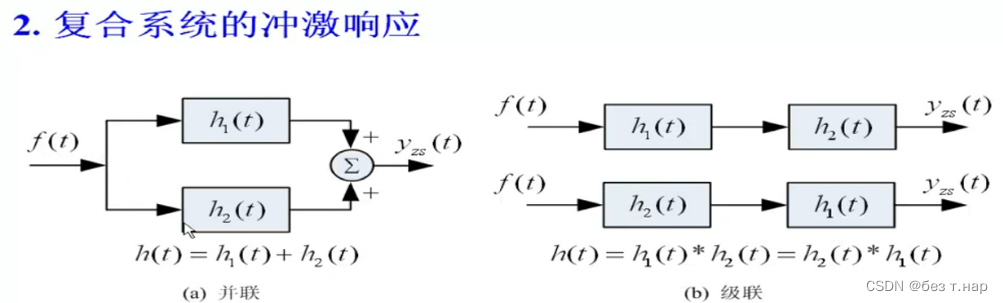
2.3 冲击响应(初始状态确定为0)

在这里插入图片描述
== 简单的h(t)组合为复杂的冲击响应==

2.4 阶跃响应(初始状态确定为0）

在这里插入图片描述
直接计算方法1

利用冲激与阶跃的关系方法2

2.5 卷积-很重要！！

可以通过信号的时域分解来推导出卷积的计算形式
在这里插入图片描述

2.5.1 卷积的基本性质

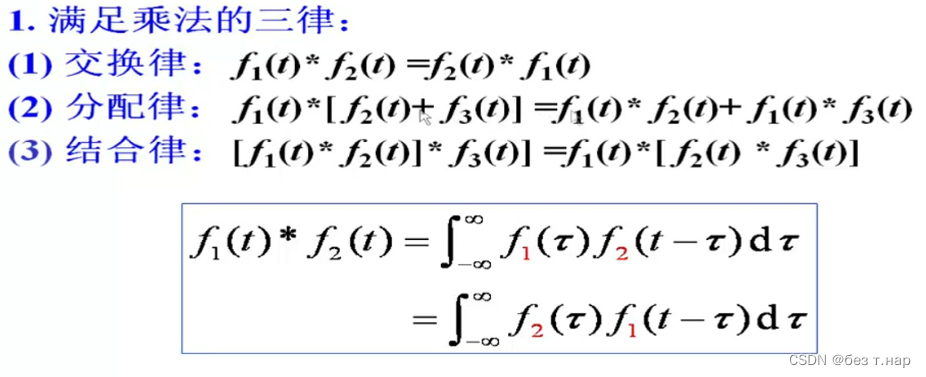
在这里插入图片描述

2.5.2 奇异函数的卷积特性

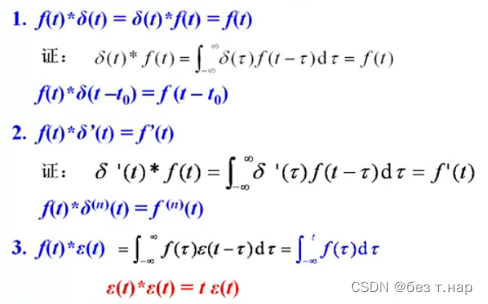
在这里插入图片描述

2.5.3 卷积的微积分性质

性质3注意使用条件
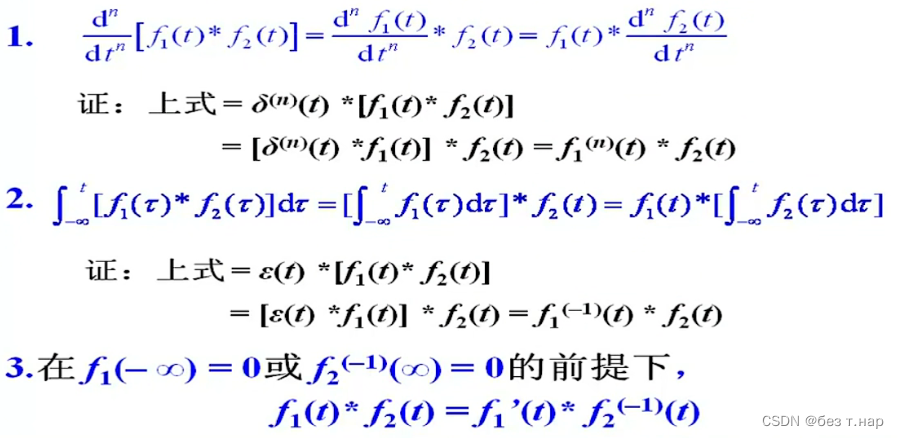
在这里插入图片描述

2.5.4 卷积的时移特性

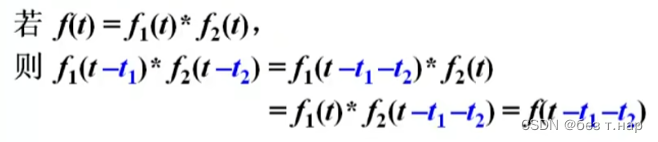
在这里插入图片描述

2.5.5 常用的卷积公式

净面积指f(t)负无穷到正无穷的积分
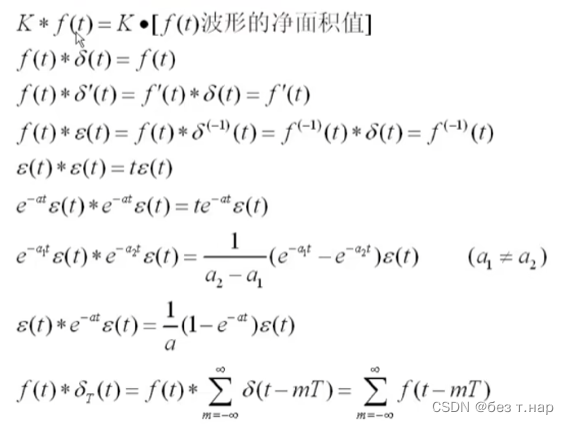
在这里插入图片描述

2.5.6 卷积的基本求解方式

定义式很重要
在这里插入图片描述

2.6 互相关与自相关函数定义

2.6.1 互相关函数

在这里插入图片描述

2.6.2 自相关函数<–关于τ的偶函数

描述的是自身与自身瞬间的相似程度
在这里插入图片描述

2.6.2 相关函数与卷积的联系

在同一自变量下比较，相关函数与卷积差一个翻折
在这里插入图片描述

2.7 微分算子

2.7.1微分算子定义

为简化微分方程描述提出微分算子
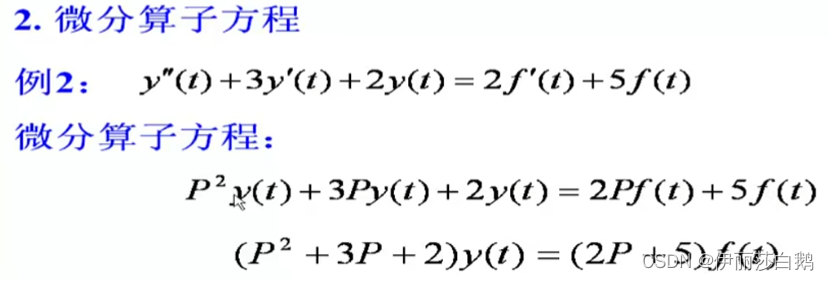
在这里插入图片描述

2.7.2微分算子性质—>可以传输算子H§去代替复杂的微分方程

在这里插入图片描述
不能顺便消项的原因
1、这里的P表示微分运算，随意消去会改变方程的阶数
2、两个函数的微分项相等不一定原函数就相等

2.7.3 RLC算子

在这里插入图片描述

3.1 离散系统—>类似连续信号去学习，

离散系统详细的在数字信号处理进行学习
1.差分基本定义
在这里插入图片描述

4.1 信号分解为正交函数

1、基本的矢量分解
在这里插入图片描述
分解到哪一个基向量上就找哪个分量

4.1.1 信号的正交–一个区间内的正交

在这里插入图片描述

K等于1则为标准正交函数集

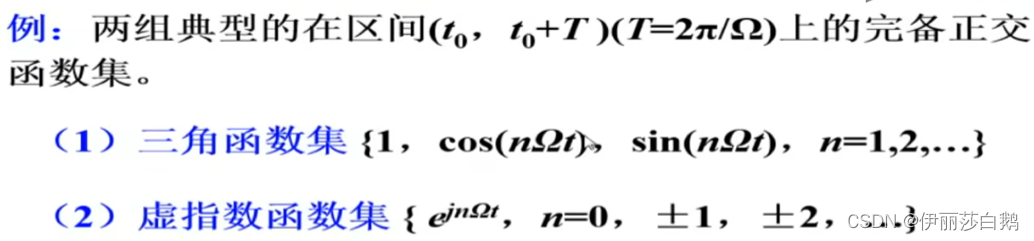
这里求每一个Cj都对其求偏导

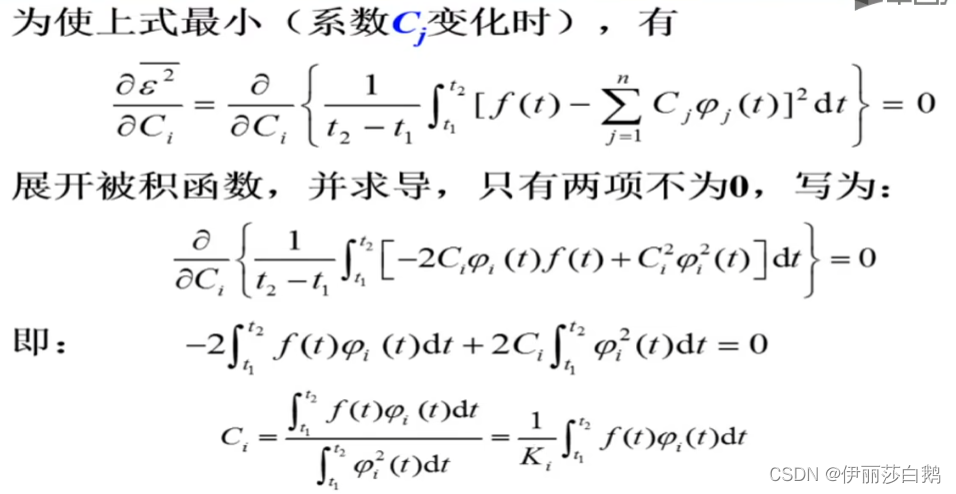
4.1.2 傅里叶级数

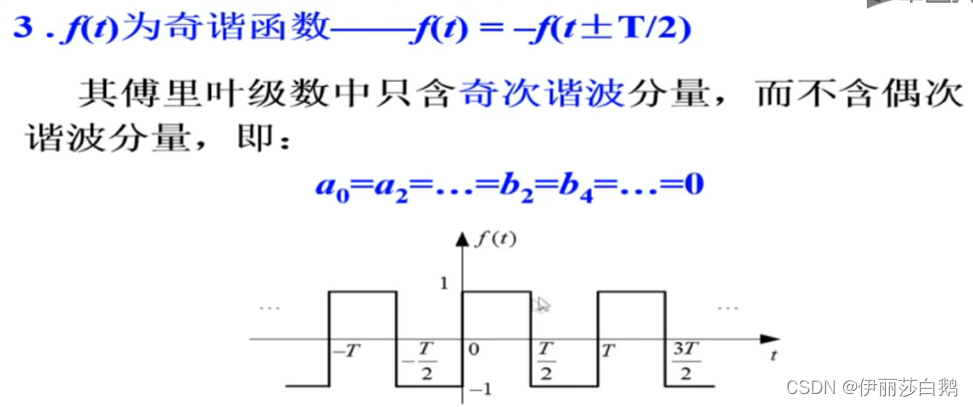
广义傅里叶级数–>正交基不确定在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

奇谐函数的傅里叶级数偶次项为0
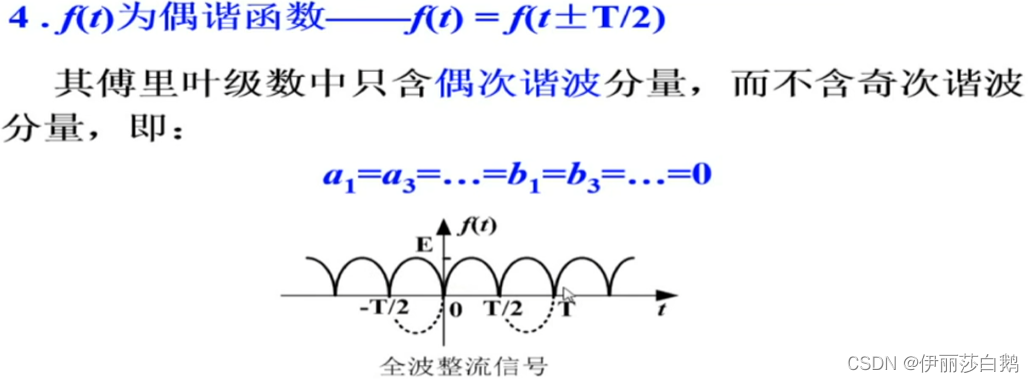
偶谐函数的傅里叶级数奇次项为0

指数函数的傅里叶级数变换

五种傅里叶变换

FT 傅里叶变换
FS 傅里叶级数
DTFS 离散时间傅里叶变换(FT的时间离散)
DFS 离散傅里叶级数(FS的时间离散)
DFT 离散傅里叶变换(DFS的主值区间，DTFS的频域离散)