Leetcode周赛370补题(3 / 3)
目录
3、在树上执行操作以后得到的最大分数 - dfs树 + 逆向思考
1、找到冠军 Ⅰ- 暴力


class Solution {
public int findChampion(int[][] g) {
int n=g.length;
for(int i=0;i<n;i++)
{
int cnt=0;
for(int j=0;j<n;j++)
if(g[i][j]==1) cnt++;
if(cnt==n-1) return i;
}
return 1;
}
}
2、找到冠军 Ⅱ - 寻找入度为0的点

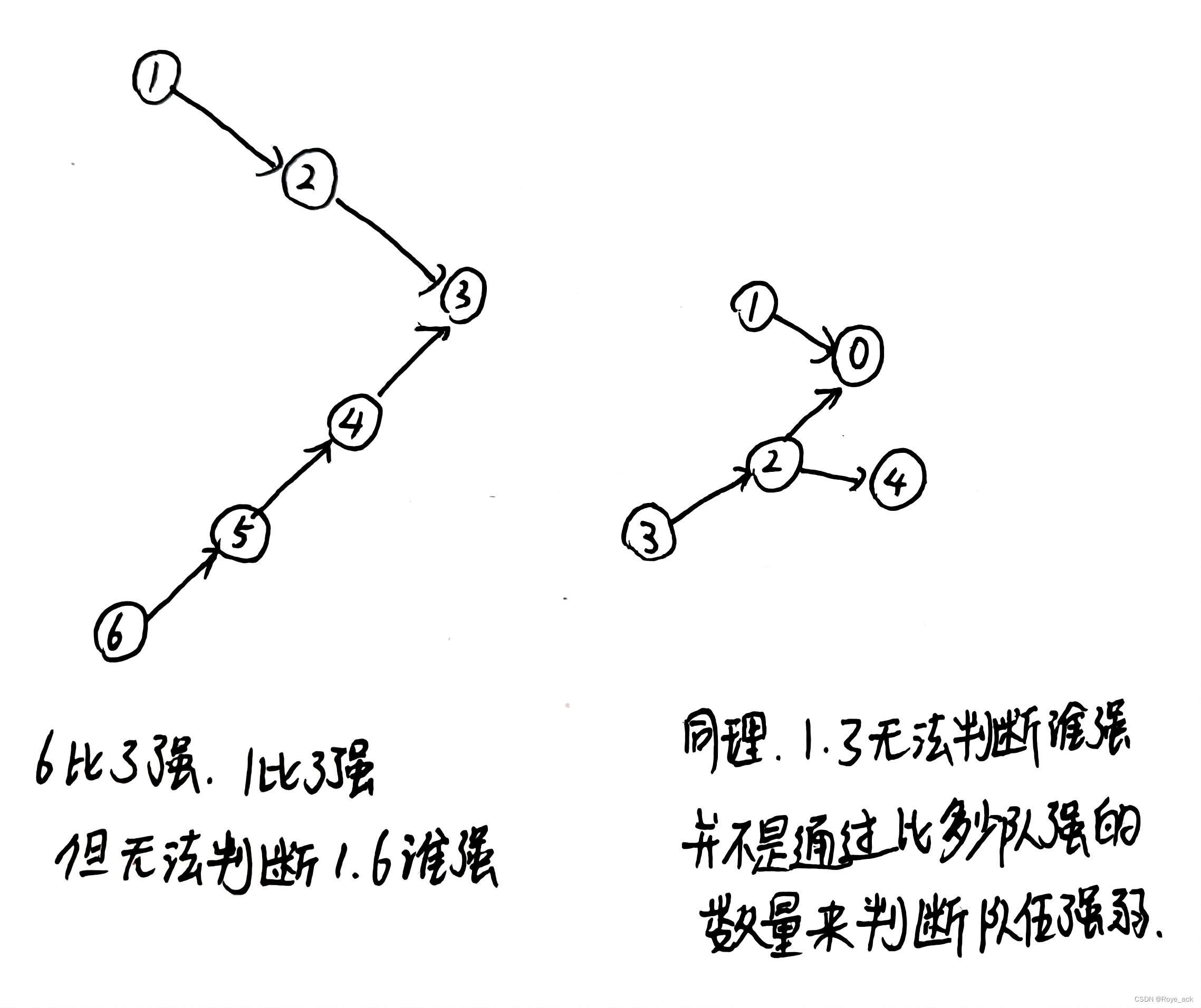
思路:
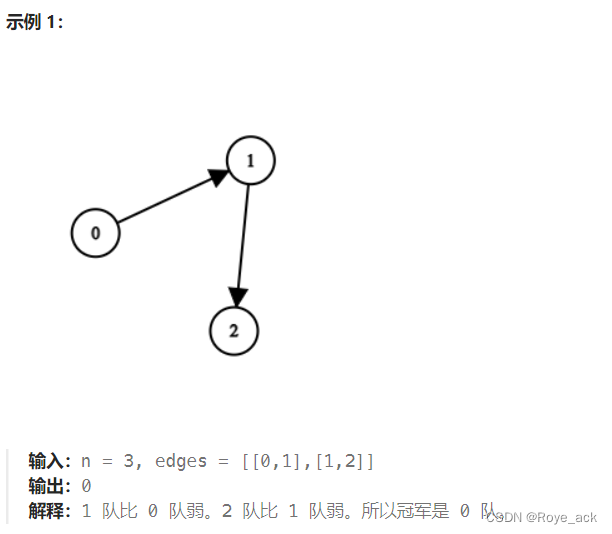
我们通过样例发现冠军点的入度肯定为0,假设有多个入度为0的点,是否能判断出谁是冠军?我们画几种情况看看
我们发现如果有多个入度为0的点,则无法判断出冠军,因为冠军并不是由战胜队伍的数量来衡量的,因此我们只需要找入度为0的点,如果有多个则返回-1
简化代码可以标记入度为0的点,然后遍历找出入度为0的点,如果出现多个则返回-1
class Solution {
public int findChampion(int n, int[][] edges) {
int[] st=new int[n];
for(int[] e:edges)
st[e[1]]=1; //将入度不为0的点标记
int res=-1;
for(int i=0;i<n;i++)
{
if(st[i]==0)
{
if(res!=-1) return -1; //如果入度为0且有多个则无法判断冠军
res=i;
}
}
return res;
}
}3、在树上执行操作以后得到的最大分数 - dfs树 + 逆向思考

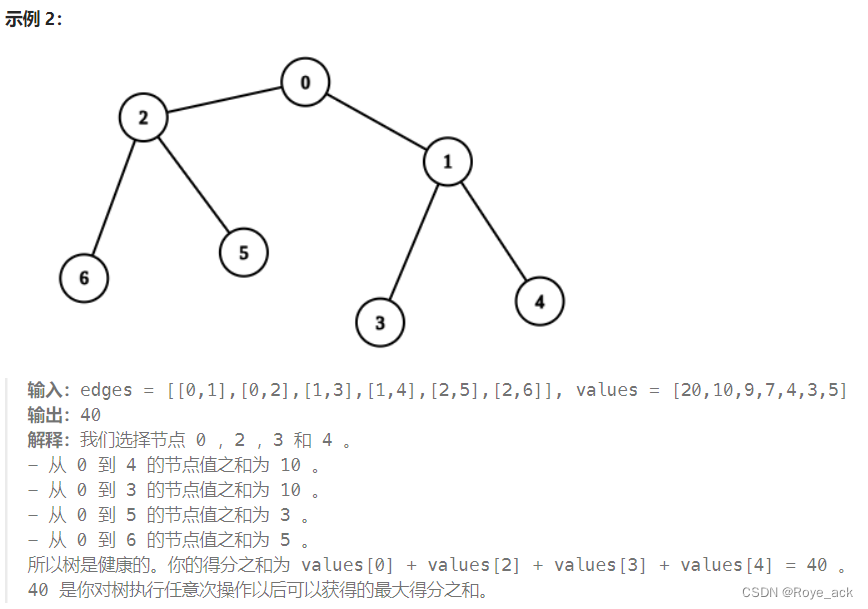

思路:
要保证这棵树是健康的,且要保证得分最大,即保证每条分支至少保留一个节点不操作(保证该路径和不为0)
所以问题转换为找出每个分支满足健康情况下的【代价和最小】的不操作点
则操作点最大代价和 = 总代价 - 不操作点最小代价和
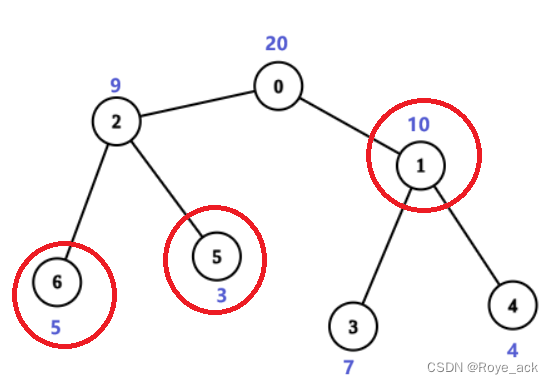
如下图,选2,5,6为不操作点,则能保证每条分支代价和均不为0,且价值最大
我们设dfs(x)为以x为根节点的健康子树中不操作节点的最小代价
其中cnt为以cur为根节点的子树的最小代价和
则答案=总value - dfs(0) 【整棵健康数中不操作节点的最小代价】
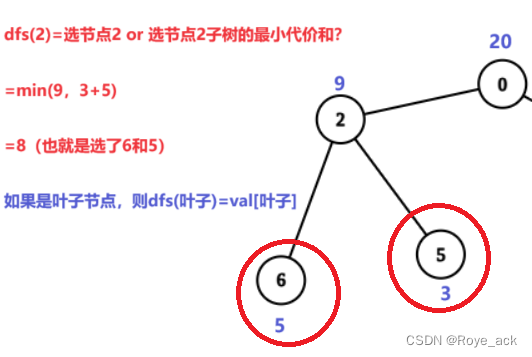
- 在dfs函数中,遍历cur节点的子节点,求出子节点的最小代价和cnt
- 返回 min(cur的价值,以cur为根节点的子树的最小代价cnt)
- 如果cur为叶子节点,则dfs值为val[cur]
为什么需要st[ ]数组标记,建双向边?
因为题目声明根节点为0,从0开始,且为无向树,因此需要双向建边
如果单向建边就会出现下面的这种错误样例
class Solution {
public long dfs(int cur,int[] v,List<Integer>[] g,int[] st )
{
long cnt=0;
for(int x:g[cur])
if(st[x]==0)
{
st[x]=1;
cnt+=dfs(x,v,g,st);
}
//cnt=0表示该节点为叶子节点
//说白了就是看:是选某子树的根节点值or根节点下子树代价和最小值
return cnt==0? v[cur]:Math.min((long)v[cur],cnt);
}
public long maximumScoreAfterOperations(int[][] edges, int[] values) {
int n=values.length;
List<Integer>[] g=new ArrayList[n+1];
for(int i=0;i<n;i++) g[i]=new ArrayList<>();
int[] st=new int[n+1];
long res=0;
for(int x:values) res+=x;
//建树
for(int[] e:edges)
{
g[e[0]].add(e[1]);
g[e[1]].add(e[0]);
}
st[0]=1;
return res-dfs(0,values,g,st); //dfs(x)表示以x为根节点的健康子树中不操作节点的最小代价
//最大代价 = 总代价 - 不操作节点的最小代价和
}
}