程序员心中应该有点B树
目录
前言
大家好,今天给大家介绍一下B树
一 . 基本搜索结构
| 种类 | 数据格式 | 时间复杂度 |
| 顺序查找 | 无要求 |  |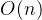
| 二分查找 | 有序 |  |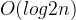
| 二叉搜索树 | 无要求 |  |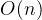
| 二叉平衡树 | 无要求-最后随机 |  |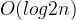
| 哈希 | 无要求 |  |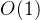
| 位图 | 无要求 |  |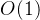
| 布隆过滤器 | 无要求 |  |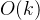
以上结构适合用于数据量不是很大的情况，如果数据量非常大，一次性无法加载到内存中，使用上述结构就不是很 方便。比如：使用平衡树搜索一个大文件
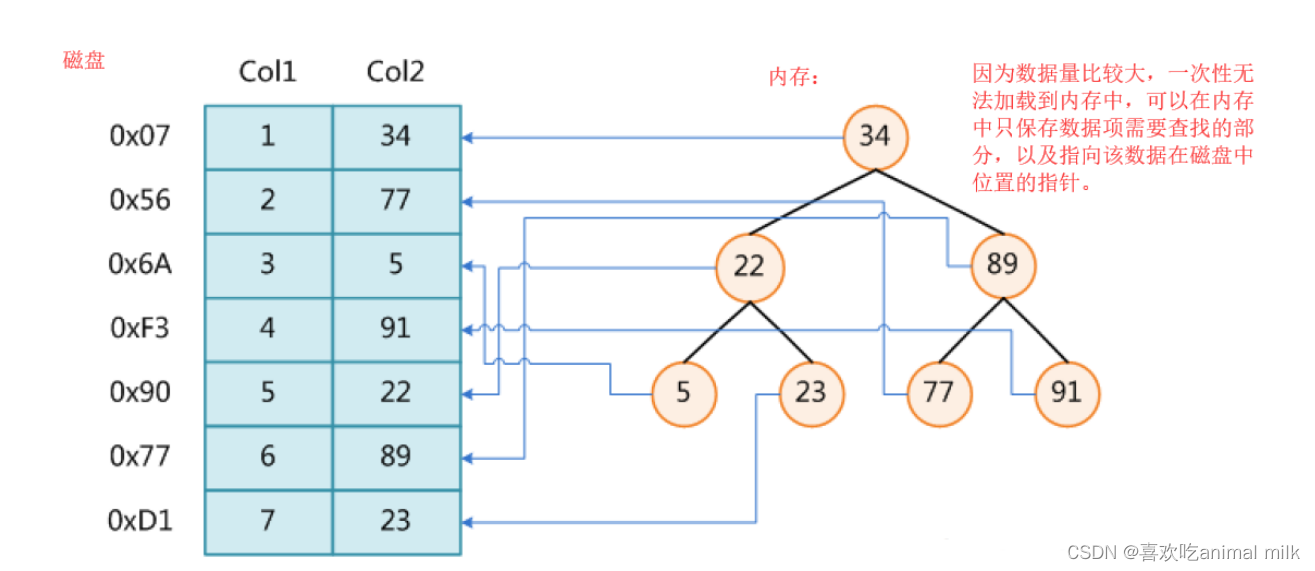
上面方法其实只在内存中保存了每一项数据信息中需要查找的字段以及数据在磁盘中的位置，整体的数据实际也在 磁盘中。
缺陷：
1. 树的高度比较高，查找时最差情况下要比较树的高度次
2. 数据量如果特别大时，树中的节点可能无法一次性加载到内存中，需要多次IO
注: 一般来说，内存的读写速度通常在几十GB/s的数量级，而传统机械硬盘的读写速度通常在几十MB/s到几百MB/s的数量级，因此磁盘I/O的速度通常比内存的速度慢几个数量级，可以达到1000倍以上的差距。这个差距在现代计算机系统中是非常显著的。当然，随着固态硬盘（SSD）等新技术的发展，磁盘的速度已经有所提高，但仍然远远落后于内存的速度。
那如何加速对数据的访问呢？
1. 提高IO的速度
2. 降低树的高度---多叉树平衡树(减少IO次数)
二 . B-树的概念
1970年，R.Bayer和E.mccreight提出了一种适合外查找的树，它是一种平衡的多叉树，称为B树(有些地方写的是B树，注意不要误读成"B减树")。一棵M阶(M>2)的B树，是一棵平衡的M路平衡搜索树，可以是空树或者满足一下性 质：
1. 根节点至少有两个孩子
2. 每个非根节点至少有M/2-1(上取整)个关键字,至多有M-1个关键字，并且以升序排列
例如：当M=3的时候，至少有3/2=1.5，向上取整等于2，2-1=1个关键字，最多是2个关键字
3. 每个非根节点至少有M/2(上取整)个孩子,至多有M个孩子
例如：当M=3的时候，至少有3/2=1.5，向上取整等于2个孩子。最多有3个孩子。
4. key[i]和key[i+1]之间的孩子节点的值介于key[i]、key[i+1]之间
5. 所有的叶子节点都在同一层
三 . B-树的插入分析
为了简单起见，假设M = 3. 即三叉树，每个节点中存储两个数据，两个数据可以将区间分割成三个部分，因此节点 应该有三个孩子，为了后续实现简单期间，节点的结构如下：
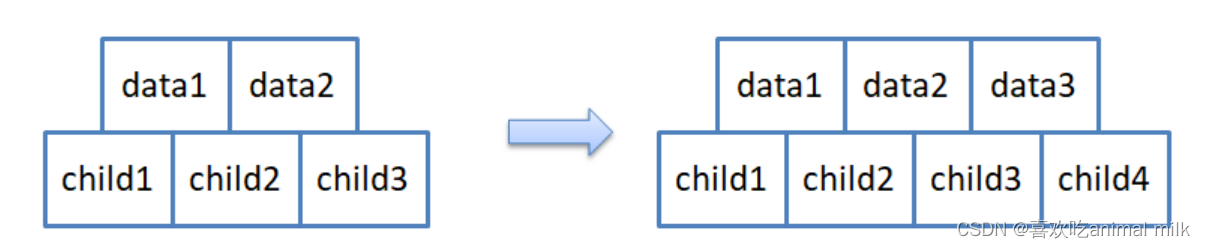
注意：孩子永远比数据多一个。此处为了分裂简单,关键字数组和孩子数组多给一个元素
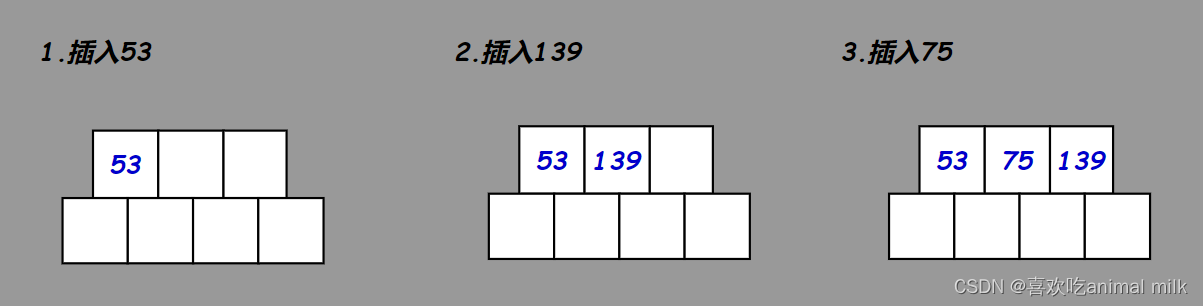
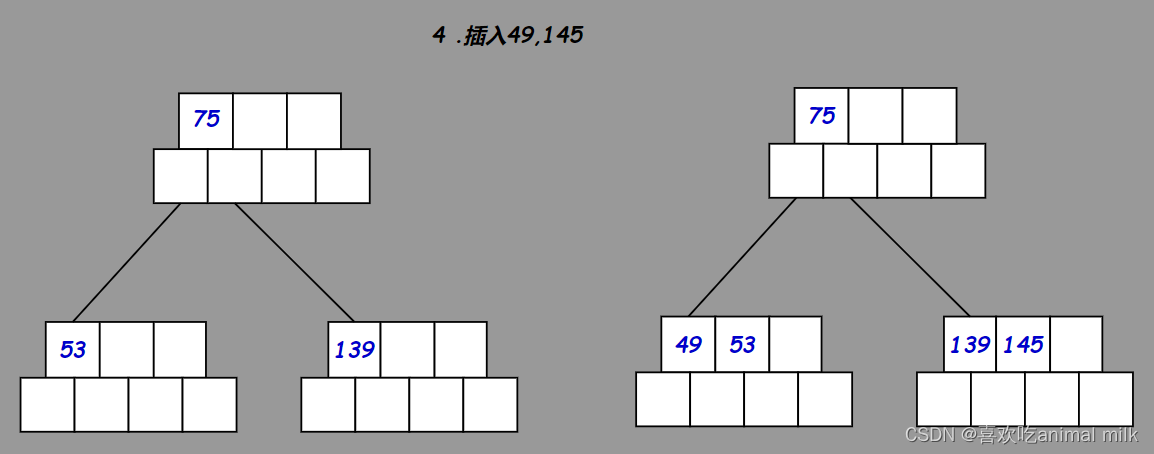
用序列{53, 139, 75, 49, 145, 36, 101}模拟构建B树的过程如下：
正常插入: 按照插入排序找插入位置
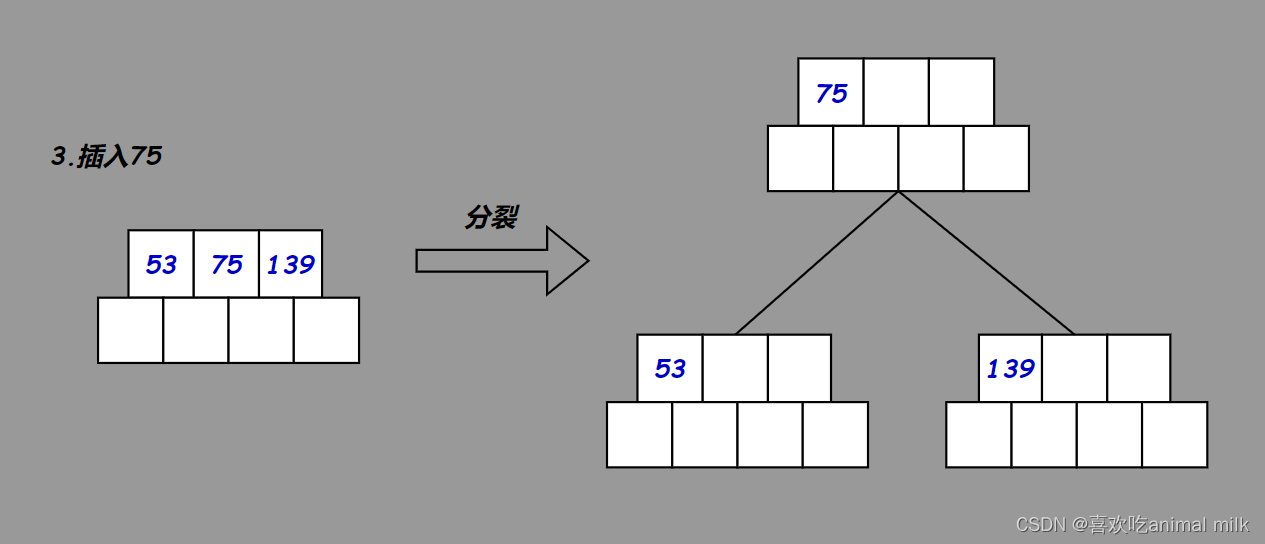
分裂步骤:
- 找到节点数据域的中间位置
- 给一个新节点，将中间位置的数据搬移到新节点中
- 将中间位置数据搬移到父节点中
- 将节点连接好
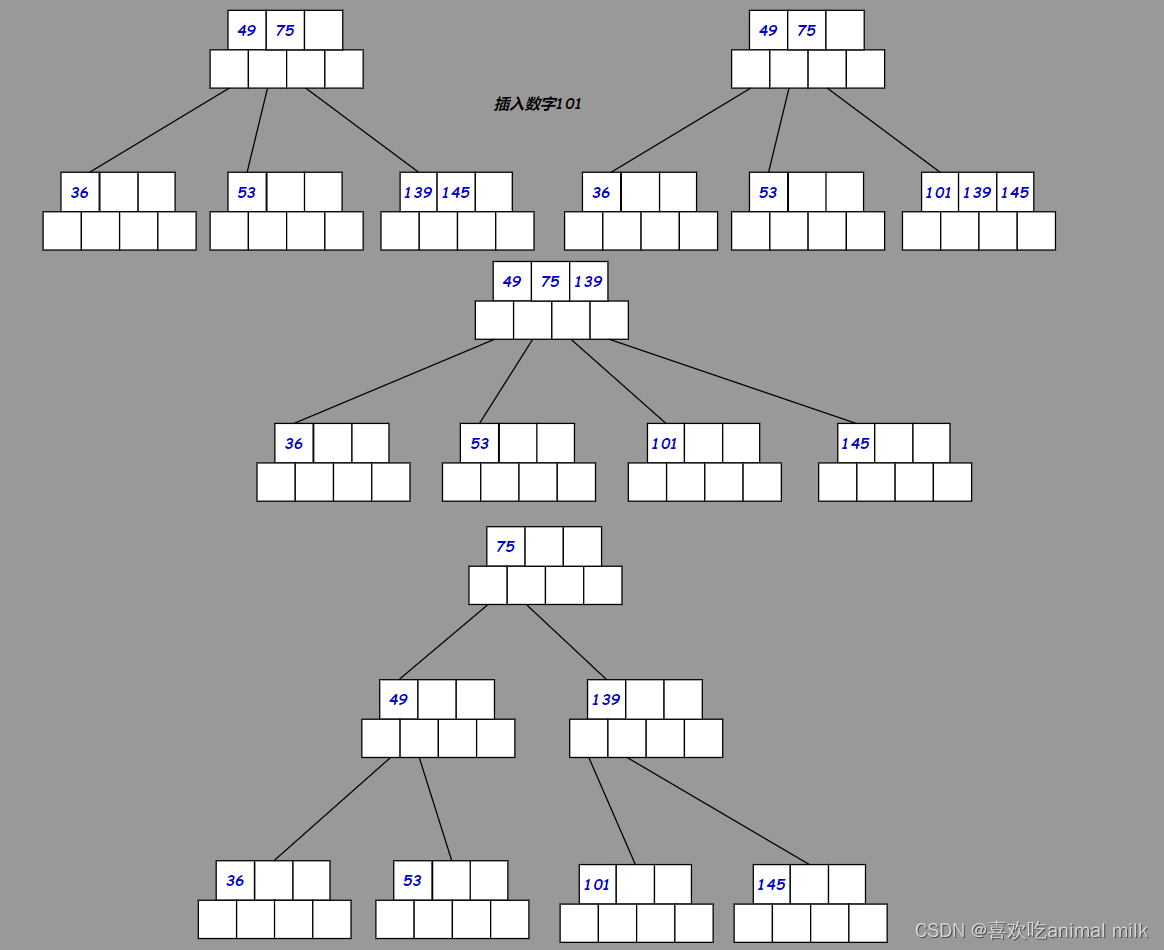
插入过程总结：
1. 如果树为空，直接插入新节点中，该节点为树的根节点
2. 树非空，找待插入元素在树中的插入位置(注意：找到的插入节点位置一定在叶子节点中)
3. 检测是否找到插入位置(假设树中的key唯一，即该元素已经存在时则不插入)
4. 按照插入排序的思想将该元素插入到找到的节点中
5. 检测该节点是否满足B-树的性质：即该节点中的元素个数是否等于M，如果小于则满足
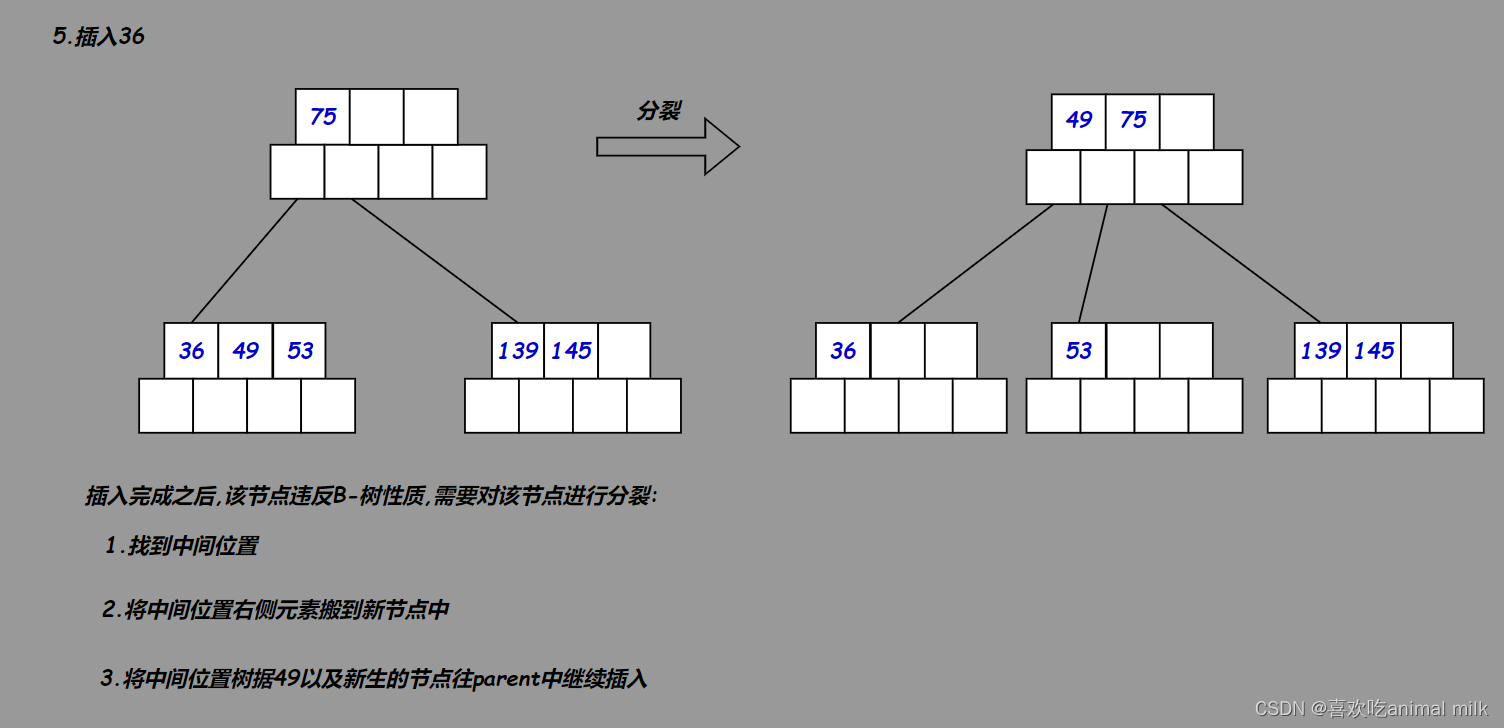
6. 如果插入后节点不满足B树的性质，需要对该节点进行分裂：
- 申请新节点
- 找到该节点的中间位置
- 将该节点中间位置右侧的元素以及其孩子搬移到新节点中
- 将中间位置元素以及新节点往该节点的双亲节点中插入，即继续4
7. 如果向上已经分裂到根节点的位置，插入结束
四 . B树的插入实现
4.1 B-树的节点设计
public class MyBTree { private static int M; static class BTRNode { public int[] keys; // 存放当前节点中的元素key public BTRNode[] subs; // 存放当前节点的孩子节点 public BTRNode parent; // 在分裂节点后可能需要继续向上插入，为实现简单增加 parent域 public int usedSize; // 节点当中关键字的数量 public BTRNode() { // 这里多给一个,好分裂 this.keys = new int[M]; this.subs = new BTRNode[M+1]; } } public MyBTree(int M){ MyBTree.M = M; }}
查找节点
private Pair<BTRNode,Integer> findNode(int key) {
BTRNode cur = root;
BTRNode parent = null;
while(cur != null){
int i = 0;
while(i < cur.usedSize){
if(cur.keys[i] == key){
// 找到了,返回一个当前找到的节点,和节点在keys数组中的下标
return new Pair<>(cur,i);
}else if(cur.keys[i] < key){
i++;
}else {
break;
}
}
// 在cur节点的第index的孩子节点中找key
parent = cur;
cur = cur.subs[i];
}
// 没找到,返回parent和-1
return new Pair<>(parent,-1);
}pair代表节点和下标的关联关系
public class Pair <k,v>{
private k key;
private v value;
public Pair() {
}
public Pair(k key, v value) {
this.key = key;
this.value = value;
}
public k getKey() {
return key;
}
public void setKey(k key) {
this.key = key;
}
public v getValue() {
return value;
}
public void setValue(v value) {
this.value = value;
}
}/**
* 往b树中插入一个节点
* @param key
* @return
*/
public boolean insert(int key){
BTRNode node = new BTRNode();
// 1.如果root为空
if(root == null){
root = node;
root.keys[0] = key;
root.usedSize++;
return true;
}
// 2.当b树不为空的时候,我们要看b树中是否存在我们当前的key
Pair<BTRNode,Integer> pair = findNode(key);
// 找到了,返回false;
if(pair.getValue() != -1)
{
return false;
}
// 没找到,按照插入排序将当前节点插入b树
BTRNode parent = pair.getKey();
int index = parent.usedSize-1;
for(; index>=0; index--){
if(parent.keys[index] >= key){
parent.keys[index+1] = parent.keys[index];
}else{
break;
}
}
parent.keys[index+1] = key;
parent.usedSize++;
// 插入完成之后判断是否达到分裂的临界值.如果达到了分裂条件,进行分裂
if(parent.usedSize >= M){
// 分裂
split(parent);
}
return true;
}了解了解就行,估摸着用不到,思想 > 一切
private void split(BTRNode cur) {
BTRNode newNode = new BTRNode();
// 将父亲节点记录
BTRNode parent = cur.parent;
int mid = cur.usedSize>>1;
int i = mid+1;
int j = 0;
for(;i< cur.usedSize; i++){
newNode.keys[j] = cur.keys[i];
newNode.subs[j] = cur.subs[i];
if(newNode.subs[j] != null){
newNode.subs[j].parent = newNode;
}
j++;
}
// 多拷贝一次孩子
newNode.subs[j] = cur.subs[i];
if(newNode.subs[j] != null){
newNode.subs[j].parent = newNode;
}
newNode.usedSize = j;
// 这里多减的一是指要提到父亲节点的key
cur.usedSize = cur.usedSize-j-1;
// 特殊
if(cur == root){
root = new BTRNode();
root.keys[0] = cur.keys[mid];
root.subs[0] = cur;
root.subs[1] = newNode;
root.usedSize++;
cur.parent = root;
newNode.parent = root;
return;
}
// 更新当前节点的父亲节点
newNode.parent = parent;
// 开始移动父亲节点
int endT = parent.usedSize-1;
int midVal = cur.keys[mid];
for(;endT>=0; endT--){
if(parent.keys[endT] > midVal){
parent.keys[endT+1] = parent.keys[endT];
parent.subs[endT+2] = parent.subs[endT+1];
}else{
break;
}
}
parent.keys[endT+1] = midVal;
parent.subs[endT+2] = newNode;
parent.usedSize++;
if(parent.usedSize >= M){
split(parent);
}
}五 . B-树的性能分析
对于一棵节点为N度为M的B-树，查找和插入需要 ~ 次比较，这个很好证明：对于度为M的B树，每一个节点的子节点个数为M/2 ~(M-1)之间，因此树的高度应该在要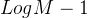
N 和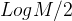 
N之间，在定位到该 节点后，再采用二分查找的方式可以很快的定位到该元素。
B-树的效率是很高的，对于N = 62*1000000000个节点，如果度M为1024，则 <= 4，即在620亿个元素 中，如果这棵树的度为1024，则需要小于4次即可定位到该节点，然后利用二分查找可以快速定位到该元素，大大 减少了读取磁盘的次数。
六 . B+树和B*树
6.1 B+树
B+树是B树的变形，也是一种多路搜索树：
1. 其定义基本与B-树相同，除了：
2. 非叶子节点的子树指针与关键字个数相同
3. 非叶子节点的子树指针p[i]，指向关键字值属于【k[i]，k[i+1])的子树
4. 为所有叶子节点增加一个链指针
5. 所有关键字都在叶子节点出现
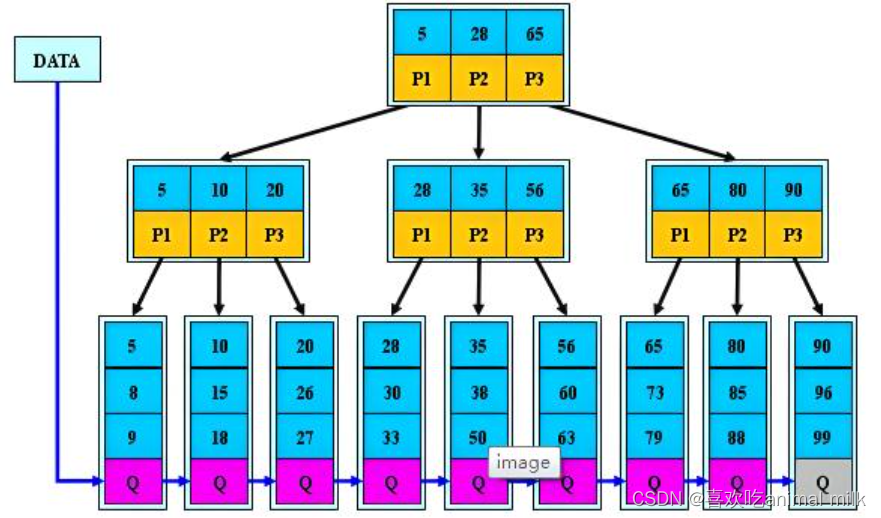
B+树的搜索与B-树基本相同，区别是B+树只有达到叶子节点才能命中(B-树可以在非叶子节点中命中)，其性能也等 价与在关键字全集做一次二分查找。
B+树的特性：
1. 所有关键字都出现在叶子节点的链表中(稠密索引)，且链表中的节点都是有序的。
2. 不可能在非叶子节点中命中。
3. 非叶子节点相当于是叶子节点的索引(稀疏索引)，叶子节点相当于是存储数据的数据层。
4. 更适合文件索引系统
6.2 B*树
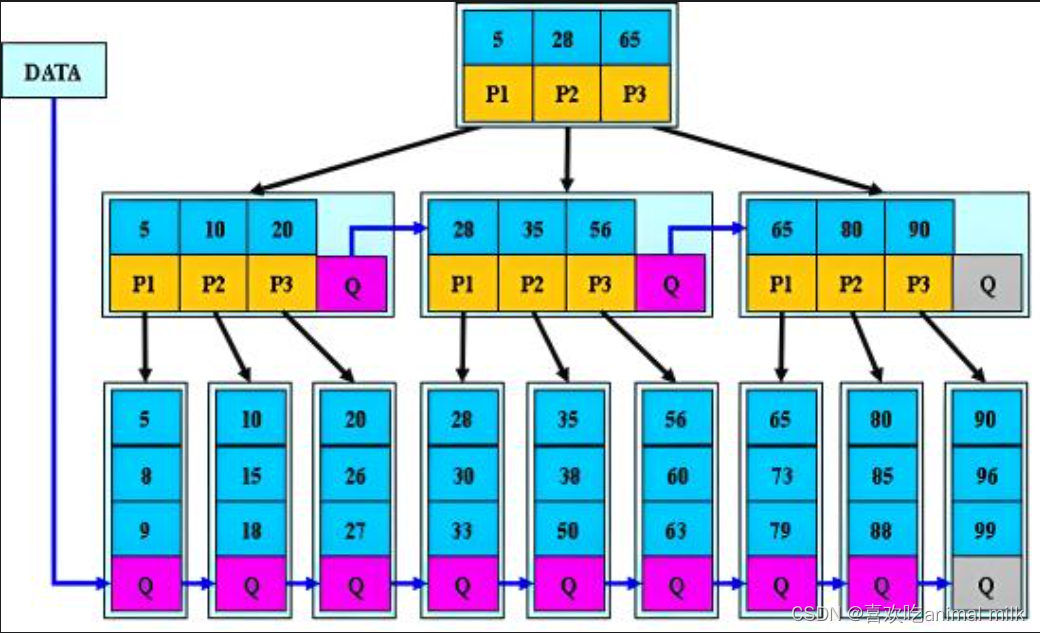
B*树和B+树都是B树的变种，它们在某些方面有相似之处，但也存在一些关键的区别。
-
叶子节点连接：B*树中的叶子节点之间会形成一个链表，这样方便范围查询和区间扫描的实现。而B+树中的叶子节点也形成一个有序链表，但是内部节点并不参与这个链表，只有叶子节点之间有连接。
-
节点填充：B*树中的非叶子节点相比B+树更加填充，即每个非叶子节点中的关键字个数更多，这样可以减少树的高度，提高查询效率。而B+树中的非叶子节点只存储索引信息，不存储实际的数据，因此非叶子节点中的关键字个数相对较少。
-
节点分裂：B*树中节点的分裂相对于B+树更加激进，当一个节点中的关键字个数达到阈值时，会立即进行分裂，而不是像B+树那样等到节点填满后再分裂。
B树定义了非叶子节点中关键字的个数至少为2/3M，其中M为节点的最大关键字个数。这个设计使得B树更加填充，减少了树的高度，提高了查询效率。这是B*树相对于传统B树的一个优化。
总结
这篇博客就到这里,我们下一篇博客见!