Improved Variational Inference with Inverse Autoregressive Flow
概
一种较为复杂normalizing flow.
主要内容
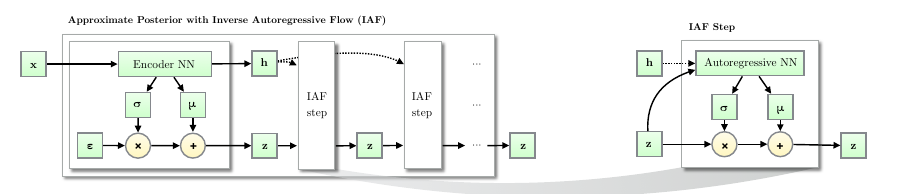
IAF的流程是这样的:
- 由encoder 得到
μ
,
σ
,
h
\mu, \sigma, h
μ,σ,h, 采样
ϵ
\epsilon
ϵ, 则
z 0 = μ 0 + σ 0 ⊙ ϵ ; z_0 = \mu_0 + \sigma_0 \odot \epsilon; z0=μ0+σ0⊙ϵ; - 由自回归模型得到
μ
1
,
σ
1
\mu_1, \sigma_1
μ1,σ1, 则
z 1 = μ 1 + σ 1 ⊙ z 0 ; z_1 = \mu_1 + \sigma_1 \odot z_{0}; z1=μ1+σ1⊙z0; - 依次类推:
z t = μ t + σ t ⊙ z t − 1 ; z_t = \mu_t + \sigma_t \odot z_{t-1}; zt=μt+σt⊙zt−1;
自回归模型的特点就是:
v
^
=
f
(
v
)
,
f
:
R
D
→
R
D
,
\hat{v} = f(v), \quad f: \mathbb{R}^D \rightarrow \mathbb{R}^D, \\
v^=f(v),f:RD→RD,
∇
v
f
\nabla_v f
∇vf是一个对角线元素为0的下三角矩阵.
我们来看
∇
z
t
−
1
z
t
\nabla_{z_{t-1}}z_{t}
∇zt−1zt,
∇
z
t
=
∇
μ
t
+
d
i
a
g
(
z
t
−
1
)
∇
σ
t
+
d
i
a
g
(
σ
t
)
.
\nabla z_t = \nabla \mu_t + \mathrm{diag}(z_{t-1}) \nabla \sigma_t + \mathrm{diag}(\sigma_t).
∇zt=∇μt+diag(zt−1)∇σt+diag(σt).
显然,
∇
z
t
−
1
z
t
\nabla_{z_{t-1}} z_t
∇zt−1zt也是一个对角线元素为0的下三角矩阵, 且
d
e
t
∇
z
t
=
d
e
t
d
i
a
g
(
σ
t
)
=
∏
i
=
1
D
(
σ
t
)
i
.
\mathrm{det} \nabla z_t = \mathrm{det} \: \mathrm{diag}(\sigma_t)= \prod_{i=1}^D (\sigma_t)_i.
det∇zt=detdiag(σt)=i=1∏D(σt)i.
这个计算方式就相当简单了.
总结一下, 最后的
log
q
(
z
T
∣
x
)
=
−
∑
i
=
1
D
(
1
2
ϵ
i
2
+
1
2
log
(
2
π
)
+
∑
t
=
0
T
log
σ
t
,
i
)
.
\log q(z_T|x) = -\sum_{i=1}^D( \frac{1}{2} \epsilon_i^2 + \frac{1}{2}\log (2\pi) + \sum_{t=0}^T \log \sigma_{t,i}).
logq(zT∣x)=−i=1∑D(21ϵi2+21log(2π)+t=0∑Tlogσt,i).