第五单元用python学习微积分（三十五）幂级数和泰勒级数下

本文内容来自于学习麻省理工学院公开课：单变量微积分-期末复习-网易公开课

Bullseye：第五单元用python学习微积分（三十四）泰勒级数

Bullseye：第三单元用python学习微积分（十九）FTC2（下）和定积分在对数和几何上的应用

一、幂级数（Power series）

1、复习

（1）有一个数字R，编辑, 当 |x| < R , 级数的和是收敛的，当 |x| > R , 级数的和是发散的，R就被称作衰减半径。

（2）当 |x| < R，也就是在收敛半径内部，f(x) 可以无限次就导，就像多项式求导。同时有编辑。

一、幂级数（Power series）

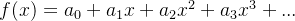
f(x) = a_0+ a_1x + a_2x^2 + a_3x^3+...

多项式是幂级数的一个例子 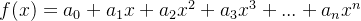f(x) = a_0+ a_1x + a_2x^2 + a_3x^3+...+a_nx^n

1、复习

（1）有一个数字R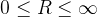， $0\leq R \leq \infty$ , 当 |x| < R , 级数的和是收敛的，当 |x| > R , 级数的和是发散的，R就被称作衰减半径。

（2）当 |x| < R，也就是在收敛半径内部，f(x) 可以无限次就导，就像多项式求导。同时有 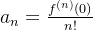$a_n=\frac{f^{(n)}(0)}{n!}$ 。

（3）可以写成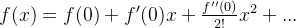： $f(x) = f(0)+f'(0)x + \frac{f''(0)}{2!} x^2 + ...$

2、例1 几何级数

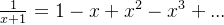
$\frac{1}{x+1} = 1-x+x^2-x^3+...$

假设有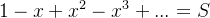 1-x+x^2-x^3+... = S

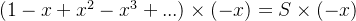
$(1-x+x^2-x^3+... )\times(- x) = S \times (-x)$

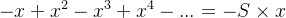
$-x+x^2-x^3+x^4-... = -S \times x$

$S -(-x+x^2-x^3+x^4-...) =S-(-S \times x)$

由于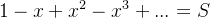 1-x+x^2-x^3+... = S

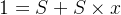
$1= S + S \times x$

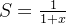$S= \frac{1}{1+x}$ （ R=1 ）

使用泰勒公式展开

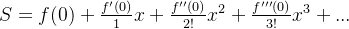
$S = f(0)+\frac{f'(0)}{1}x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)} {3!} x^3+...$

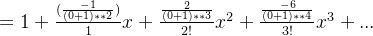
$= 1+\frac{(\frac{-1}{(0 + 1)**2})}{1}x + \frac{\frac{ 2}{(0 + 1)**3}}{2!}x^2 + \frac{\frac{-6}{(0 + 1)**4} }{3!} x^3+...$

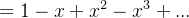
= 1-x+x^2-x^3+...

import numpy as np 
from sympy import *
import matplotlib.pyplot as plt 
figure, ax= plt.subplots( 1 ) 
ax.set_aspect( 1 ) 
def DrawXY1(xFrom,xTo,steps,expr,color,label,plt, arrow =False):
    yarr = []
    xarr = np.linspace(xFrom ,xTo, steps) 
    for xval in xarr:
        #print(expr.subs(x,xval), xval)
        yval = expr.subs(x,xval)
        yarr.append(yval)
    y_nparr = np.array(yarr) 
    x_nparr = np.array(xarr) 
    length = len (xarr)
    
    plt.plot(x_nparr, y_nparr, c=color, label=label)  
    if(arrow and steps > 2):
        plt.arrow(float(x_nparr[0]),float( y_nparr[0]),float( x_nparr[2]-x_nparr[0]),float( y_nparr[2]-y_nparr[0]), width=.02, color = color) 
        
def DrawXY(tFrom,tTo,steps,exprX,exprY, color,label,plt, arrow =False):
    xarr = []
    yarr = []
    tarr = np.linspace(tFrom ,tTo, steps) 
    for tval in tarr:
        xval = exprX.subs(t,tval)
        xarr.append(xval)
        yval = exprY.subs(t,tval)
        yarr.append(yval)
    y_nparr = np.array(yarr) 
    x_nparr = np.array(xarr) 
    length = len (xarr)
    
    plt.plot(x_nparr, y_nparr, c=color, label=label)  
    if(arrow and steps > 2):
        plt.arrow(float(x_nparr[0]),float( y_nparr[0]),float( x_nparr[2]-x_nparr[0]),float( y_nparr[2]-y_nparr[0]), width=.02, color = color) 


x = symbols('x')

expr = 1/(x+1)

DrawXY1(-0.5,2,50,expr,color='c', label=' 1/(x+1)',plt = plt, arrow = False)
DrawXY1(-3.5,-1.5,50,expr,color='c', label=' 1/(x+1)',plt = plt, arrow = False)


plt.legend(loc='lower right')
plt.show()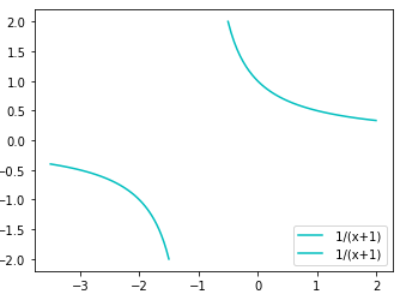

3、求取sin(x)

我们知道，当 f(x) =sin(x) 有 f'(x) = cos(x), f''(x) = -sin(x), f'''(x) = -cos(x)...

$sin(x) =\frac{sin(0)}{1} + \frac{cos(0)}{1!}x - \frac{sin(0)}{2!}x^2 - \frac{cos(0)}{3!}x^3 + \frac{sin(0)}{4!}x^4 + \frac{cos(0)}{5!}x^5 + ..$

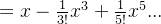
$=x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 ...$

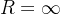
$R = \infty$

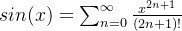
$sin(x) = \sum_{n=0}^{\infty} \frac{x^{2n+1}}{(2n+1)!}$

4、新的幂级数

（1）乘法

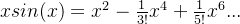
$xsin(x) =x^2 - \frac{1}{3!}x^4 + \frac{1}{5!}x^6 ...$

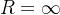
$R = \infty$

x = symbols('x')
expr = x*sin(x)
DrawXY1(0,100,50,expr,color='c', label='x*sin(x)',plt = plt, arrow = True)
plt.legend(loc='lower right')
plt.show()

（2）求导

cos(x) = sin'(x)

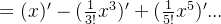
$=(x)' -( \frac{1}{3!}x^3)' + (\frac{1}{5!}x^5)' ...$

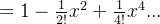
$=1 - \frac{1}{2!}x^2 +\frac{1}{4!}x^4 ...$

这与上一章中用泰勒级数展开cos(x)的结果相同

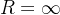
$R = \infty$

（3）积分

$\int_0^x \frac{dt}{1+t}$

由例一中几何级数展开可知

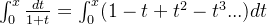
$\int_0^x \frac{dt}{1+t} = \int_0^x (1-t +t^2-t^3...)dt$

$=[t-\frac{t^2}{2}+\frac{t^3}{3}-\frac{t^4}{4}...]_0^x =x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}...$

由积分计算可知

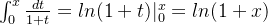
$\int_0^x \frac{dt}{1+t} = ln(1+t)|_0^x = ln(1+x)$

所以有

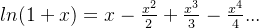
$ln(1+x) = x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}...$

由于使用的几何级数展开，同时几何级数的收敛半径为1

这个级数的收敛级数也是1

R=1

（4）变量替换

$e^{-t^2}$

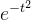
由上一章内容可知

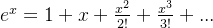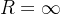$e^x = 1+x + \frac{x^2}{2!} + \frac{x^3}{3!}+...$ （ $R=\infty$ ）

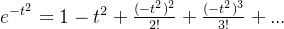
$e^{-t^2} = 1-t^2 + \frac{(-t^2)^2}{2!} + \frac{(-t^2)^3}{3!}+...$

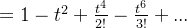
$= 1-t^2 + \frac{t^4}{2!} - \frac{t^6}{3!}+...$

误差函数:

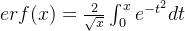
$erf(x) = \frac{2}{\sqrt{x}} \int_0^x e^{-t^2}dt$

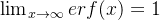（ $\lim_{x\rightarrow \infty} erf(x) =1$ ）

老师课上曾经讲过误差函数，请参考下面课程Bullseye：第三单元用python学习微积分（十九）FTC2（下）和定积分在对数和几何上的应用https://zhuanlan.zhihu.com/p/469921631

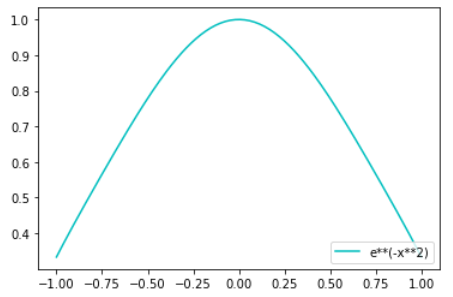
用幂级数展开

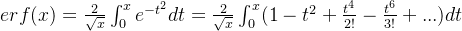
$erf(x) = \frac{2}{\sqrt{x}} \int_0^x e^{-t^2}dt = \frac{2}{\sqrt{x}} \int_0^x( 1-t^2 + \frac{t^4}{2!} - \frac{t^6}{3!}+... )dt$

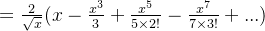
$= \frac{2}{\sqrt{x}} ( x- \frac{x^3}{3} + \frac{x^5}{5\times2!} - \frac{x^7}{7\times3!}+... )$

x = symbols('x')
expr =  1-x**2 + x**4/2  - x**6/6  
DrawXY1(-1,1,150,expr,color='c', label='e**(-x**2)',plt = plt, arrow = false)
plt.legend(loc='lower right')
plt.show()

一、幂级数（Power series）

1、复习

（1）有一个数字R， , 当 |x| < R , 级数的和是收敛的， 当 |x| > R , 级数的和是发散的，R就被称作衰减半径。

（2）当 |x| < R，也就是在收敛半径内部，f(x) 可以无限次就导，就像多项式求导。同时有 。

（3）可以写成：

2、例1 几何级数

​3、求取sin(x)

4、新的幂级数

（1）乘法

​（2）求导

（3）积分

（4）变量替换

（1）有一个数字R， $0\leq R \leq \infty$ , 当 |x| < R , 级数的和是收敛的，当 |x| > R , 级数的和是发散的，R就被称作衰减半径。

（2）当 |x| < R，也就是在收敛半径内部，f(x) 可以无限次就导，就像多项式求导。同时有 $a_n=\frac{f^{(n)}(0)}{n!}$ 。

（3）可以写成： $f(x) = f(0)+f'(0)x + \frac{f''(0)}{2!} x^2 + ...$

3、求取sin(x)

（2）求导