图像二值化阈值调整——OTSU算法(大津法/最大类间方差法)
大津算法(OTSU算法)是一种常用的图像二值化方法,用于将灰度图像转化为二值图像。该算法由日本学者大津展之于1979年提出,因此得名。
大津算法的核心思想是通过寻找一个阈值,将图像的像素分为两个类别:前景和背景。具体步骤如下:
- 统计图像的灰度直方图,得到每个灰度级的像素数目。
- 遍历所有可能的阈值(0到255),计算根据该阈值将图像分为前景和背景的类内方差。
- 根据类内方差的最小值确定最佳阈值。
在大津算法中,类内方差是衡量前景和背景之间差异的度量。通过选择使类内方差最小的阈值,可以实现最佳的图像分割效果。
大津算法的优点是简单易懂,计算效率高。它适用于灰度图像的二值化处理,特别是对于具有双峰直方图的图像效果更好。然而,该算法对于具有非双峰直方图的图像可能产生较差的分割结果。因此,在应用大津算法之前,需要对图像的直方图进行分析,确保适用性。
大津算法在图像处理中被广泛应用,例如在文档图像处理、目标检测、图像分割等领域。
下面推导类间方差函数:
设阈值为灰度k(![k\in \left [ 0,L-1 \right ],L=256](https://images2.imgbox.com/87/9e/ob2Q0GRy_o.png) )。这个阈值把图像像素分割成两类,C1类像素小于等于k,C2类像素大于k。设这两类像素各自的均值为
)。这个阈值把图像像素分割成两类,C1类像素小于等于k,C2类像素大于k。设这两类像素各自的均值为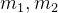 ,图像全局均值为
,图像全局均值为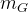 。同时像素被分为C1和C2类的概率分别为
。同时像素被分为C1和C2类的概率分别为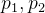 。则有:
。则有:
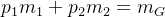
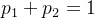
根据方差的概念,类间方差表达式为:
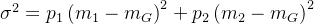
展开:
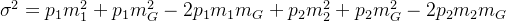
合并2,5及3,6项可得:
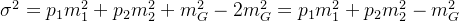
我们再把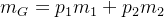 代回得到:
代回得到:
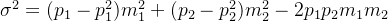
再注意到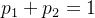 ,所以
,所以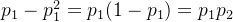 ,
,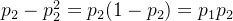 ,从而得到:
,从而得到:
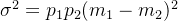
对于给定的阈值k,我们可以统计出灰度级的分布列:
| 灰度值 | 0 | 1 | ... | 255 |
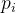 | 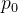 | 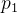 | ... | 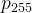 |
显然根据分布列性质有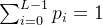 (请注意这里的
(请注意这里的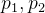 是分布列中的,不是上面的定义)
是分布列中的,不是上面的定义)
那么有:
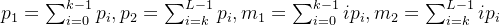
将k从![\left [ 0,L-1 \right ]](https://images2.imgbox.com/0b/a9/HcDfoNiE_o.png) 遍历,找出使得
遍历,找出使得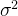 最大的k值,这个k值就是阈值。
最大的k值,这个k值就是阈值。
对于分割,这个分割就是二值化,OpenCV给了以下几种方式(同threshold):

cv2帮助文档:
首先是原理部分的实现,这部分我们使用numpy:
import cv2
import numpy as np
def OTSU(img_gray, GrayScale):
assert img_gray.ndim == 2, "must input a gary_img" # shape有几个数字, ndim就是多少
img_gray = np.array(img_gray).ravel().astype(np.uint8)
u1 = 0.0 # 背景像素的平均灰度值
u2 = 0.0 # 前景像素的平均灰度值
th = 0.0
# 总的像素数目
PixSum = img_gray.size
# 各个灰度值的像素数目
PixCount = np.zeros(GrayScale)
# 各灰度值所占总像素数的比例
PixRate = np.zeros(GrayScale)
# 统计各个灰度值的像素个数
for i in range(PixSum):
# 默认灰度图像的像素值范围为GrayScale
Pixvalue = img_gray[i]
PixCount[Pixvalue] = PixCount[Pixvalue] + 1
# 确定各个灰度值对应的像素点的个数在所有的像素点中的比例。
for j in range(GrayScale):
PixRate[j] = PixCount[j] * 1.0 / PixSum
Max_var = 0
# 确定最大类间方差对应的阈值
for i in range(1, GrayScale): # 从1开始是为了避免w1为0.
u1_tem = 0.0
u2_tem = 0.0
# 背景像素的比列
w1 = np.sum(PixRate[:i])
# 前景像素的比例
w2 = 1.0 - w1
if w1 == 0 or w2 == 0:
pass
else: # 背景像素的平均灰度值
for m in range(i):
u1_tem = u1_tem + PixRate[m] * m
u1 = u1_tem * 1.0 / w1
# 前景像素的平均灰度值
for n in range(i, GrayScale):
u2_tem = u2_tem + PixRate[n] * n
u2 = u2_tem / w2
# print(u1)
# 类间方差公式:G=w1*w2*(u1-u2)**2
tem_var = w1 * w2 * np.power((u1 - u2), 2)
# print(tem_var)
# 判断当前类间方差是否为最大值。
if Max_var < tem_var:
Max_var = tem_var # 深拷贝,Max_var与tem_var占用不同的内存空间。
th = i
return th
def main():
img = cv2.imread('6.jpg', 0)
# 将图片转为灰度图
th = OTSU(img, 256)
print("使用numpy的方法:" + str(th)) # 结果为 136
main()然后是基于cv2的OTSU实现,cv2可直接指定使用:
import cv2
import matplotlib.pylab as plt
def main2():
img = cv2.imread('6.jpg', 0)
ret, thresh1 = cv2.threshold(img, 0, 255, cv2.THRESH_OTSU)
print(ret) # 结果是135.0
titles = ['Original Image', 'After Binarization']
images = [img, thresh1]
for i in range(2):
plt.subplot(1, 2, i+1)
plt.imshow(images[i], 'gray')
plt.title(titles[i])
plt.xticks([])
plt.yticks([])
plt.show()
main2()
 https://docs.opencv.org/3.0-last-rst/modules/imgproc/doc/miscellaneous_transformations.html?highlight=threshold#threshold
https://docs.opencv.org/3.0-last-rst/modules/imgproc/doc/miscellaneous_transformations.html?highlight=threshold#threshold