人工智能和图搜索

什么是人工智能？

环顾四周，你会发现人工智能并没有一个明确且单一的定义。有人说，“人工智能被定义为对理性主体的研究”，其中“理性主体可以是任何做出决策的人、公司、机器或软件。它在考虑过去和未来后执行具有最佳结果的行动”。当前感知（代理在给定实例下的感知输入）”。其他则更哲学地试图找到人类自然智能和机器能做的事情之间的界限。

但所有的定义都试图说明，人工智能实际上是一门学科，当你想知道该做什么而你不知道该做什么时。这里出现了一个理性代理，通过一些传感器感知环境并查看它已经执行的旧操作，它尝试选择具有最佳结果的下一个操作。 

那么让我们看一个经典的寻路问题。我们有一个包含许多节点的图，您尝试找到两个节点之间成本最小的路径。这是人工智能代理的定义。你并不完全知道路径是什么，而理性主体通过感知环境（在我们的例子中是图表）会找到该路径。

但我们知道有很多算法能够解决图搜索问题。只需查看 DFS、BFS、Dijkstra 或A*即可。我们中的一些人从高中就知道这个算法。那么这里有什么新内容呢？这真的是人工智能代理所做的吗？嗯，是的，但不仅如此。人工智能不仅仅是一种编程范式，就像图搜索算法一样，而且，正如我之前所说，它是对理性主体的研究，这些理性主体研究环境并尝试选择具有最佳结果的行动。

AI 代理是一个广义的术语。它们涉及机器学习、神经网络、深度学习等等，并应用于金融、医疗机构、安全等领域。所以图搜索只是人工智能的一个小子类型。

经典的图搜索算法和能够找到两个节点之间最短路径的人工智能代理之间的区别只是术语的不同。理解这一点很重要，就像你试图创建一个与老式算法实际上没有什么不同的人工智能代理一样。

所有这些算法的要点是，在访问一个节点后，我们必须选择下一个未访问的节点并“访问”它，以查看是否达到目标。

更多关于 BFS

正如我之前所说，广度优先搜索是一种基于树的算法。它的名字来源于图遍历是分层的想法。从源节点开始，我们首先探索邻居，然后进一步向下移动。

我们看下图：

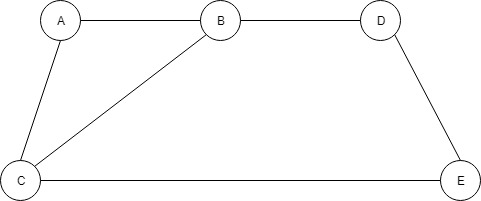
从节点 A 开始，我们看到这个图如何变成一棵树。

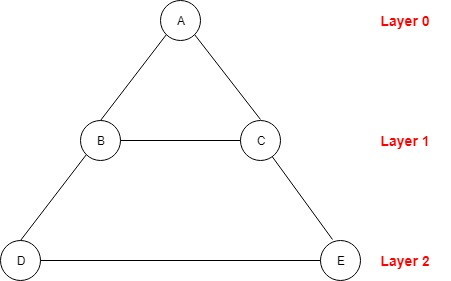
A 是位于第 0 层的起始节点，然后 B 和 C 位于第 1 层，然后 D 和 E 位于第 2 层。这就是 BFS 遍历该图的顺序。

如果我们使用 BFS 遍历该图，顺序将是：A -> B -> C -> D -> E。

仔细观察这棵树，我们会发现 B 和 C、E 和 D 之间存在一些联系。发生这种情况是因为我们的图包含循环。但如果我们想最优地遍历它，我们不应该再次访问已经访问过的节点。因此，选择要访问的节点的条件之一就是未被访问。

算法如何工作

考虑到，在访问起始节点之后，我们将继续访问它的所有邻居，然后我们将进入下一个“层”，并且需要一个队列。当我们访问一个节点时，我们检查它的邻居，如果尚未访问邻居，我们将它们添加到队列中。然后，我们实际上只是从队列中选择下一个要访问的节点。我们需要做的另一件事是标记已访问的节点，以便不再访问它们。这样，我们将只访问所有图节点一次。

寻找成本最低的路径

让我们通过在顶点上添加一些成本来更改我们的图。

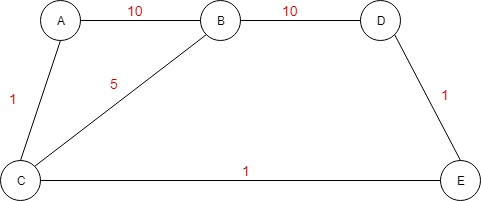
现在我们想从A到D走成本最低的路径。我们看到从 A 到D有多种方法。我们可以走这条路径，A -> B -> D，成本为 20，或者我们可以选择 A -> C -> B -> D，成本较低，为 16。但是还有另一条成本最低的路径3、A -> C -> E -> D。 那么，我们应该怎么做才能找到这条路径呢？我们需要改变获取下一个节点访问的方式。在经典的BFS算法中，我们采用先进先出的队列顺序（先进先出）来选择下一个要访问的节点。我们最终会找到目标，但不是最便宜的路径。为了以最低的成本到达路径上的目标，我们需要改变从队列中获取下一个要访问的节点的方式。

我将向您介绍的算法称为统一成本搜索，它是 Dijkstra 的稍微修改版本，当我们找到目的地时我们就停下来。经典的 Dijkstra 算法继续访问所有节点，直到队列为空，找到图中从起始节点到每个其他节点的最小成本。与 BFS 不同的是，这里我们必须存储一个新值，表示从开始到当前访问节点迄今为止的总成本。

队列不会按 FIFO 规则排序，而是根据当前到目前为止的成本值对队列进行排序，优先考虑迄今为止成本最低的未访问节点。