谈谈距离度量方式:欧氏距离与余弦距离
前因
在机器学习/深度学习的很多任务中,我们通常会面临着两个样本之间相似度的比较。通常常用的两种度量方式为欧氏距离与余弦距离,那么在什么时候用欧氏距离?什么时候用余弦相似度?他们之间的联系与区别在哪里呢?
探索
在机器学习当中,通常以一组向量来表示样本
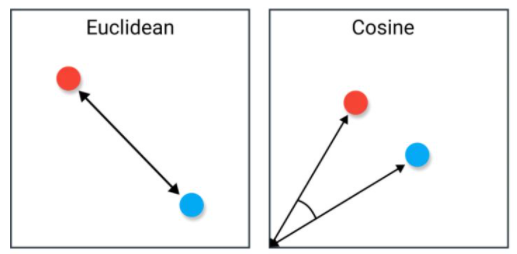
如上图所示,欧式距离是通过勾股定理来计算两个向量之间的距离:
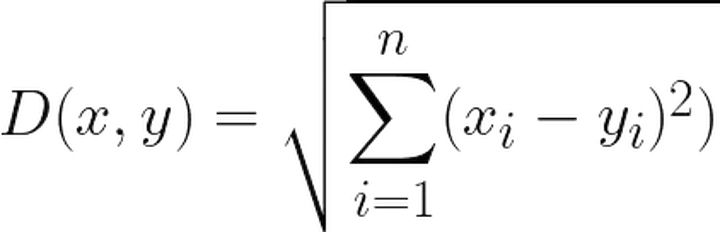
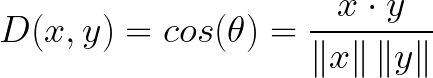
通常用1-D(x,y)来表示余弦距离。
分析:
首先谈谈区别,欧氏距离的范围是不确定的(没有经过归一化),得到的值可能很大(最小为0),值越大表示样本之间越不相似,直观上的理解就是度量两个向量点之间的绝对距离(用一根绳子去连接两个点,这根绳子的长度就是欧式距离)。而余弦距离不考虑向量大小,只关注角度关系,取值范围[-1,1],当两个向量方向完全一致时取1,完全相反时取-1。可以这么说,欧氏距离体现数值上的绝对差异,而余弦距离体现方向上的相对差异。
接下来谈谈两者的缺点与应用场景,欧氏距离尝尝收到维度诅咒,当研究对象的维度很高时(通常深度网络输出一个高维向量)会受到影响,导致范围不固定,含义也比较模糊。余弦距离虽然没有受到维度诅咒,但其并没有考虑到向量的大小,只考虑了方向。
所以,应用何种距离度量函数取决于具体的应用场景:当数据维度较低,或者向量的大小很重要时采用欧氏距离,比如在分析房价时,考虑小区绿化面积与房屋面积为特征,两个样本(1000,100)与(500,50),若采用余弦距离会认为这两个房子价格较近,这肯定是不合理的。当数据维度较高(很难判断各维度之间的具体含义),或者为稀疏向量,又或者是更关于两者的相对差异时采用余弦距离:比如分析用户行为来构建推荐系统,A用户购买向量为(1,0),B用户购买向量为(0,1)。
这里的应用限制不一定对,具体情况具体分析。比如,当维度高的时候,欧氏距离也可能效果更好。
最后谈谈它们的联系,如果我们将向量归一化后执行欧氏距离,其与余弦距离等价。公式证明见下:
来自参考链接[1]
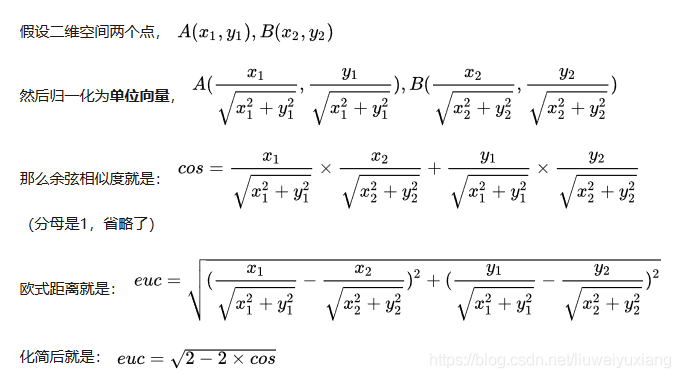
这里通过画图可以更简单地理解,当向量执行归一化后变为单位向量,欧式距离就是求单位向量之间的距离,余弦距离求夹角的余弦值:
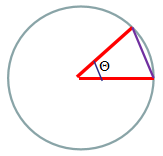
其中两个向量用红线表示,紫线表示它们之间的欧氏距离,cosΘ为余弦距离,由余弦定理可知,两者存在反比关系。
更多的度量方式见参考链接2
扩展
余弦距离是否是严格意义上的距离?
距离的定义:在一个集合中,如果每一对元素均可唯一确定一个实数,使得三条距离公理(正定性,对称性,三角不等式)成立,则该实数可称为这对元素之间的距离。
这里简单提一下,后续有时间再补充。余弦距离满足正定性和对称性,但是不满足三角不等式,因此它并不是严格 定义的距离。
参考
[1] 数据科学中常见的9种距离度量方法,内含欧氏距离、切比雪夫距离等
https://zhuanlan.zhihu.com/p/350744027
[2] 欧氏距离和余弦相似度的区别是什么?
https://www.zhihu.com/question/19640394/answer/207795500