前馈神经网络
前馈神经网络(全连接神经网络)
1、 概念及组成
前馈神经网络:每层神经元与下层神经元相互连接,神经元之间不存在同层连接,也不存在跨层连接。
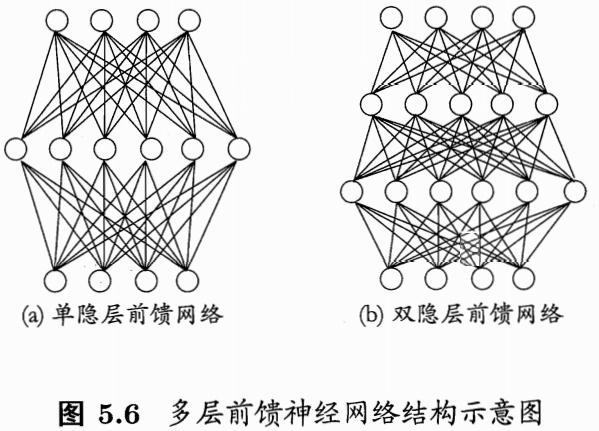
组成:输入层、隐藏层、输出层
常用神经元:M-P神经元
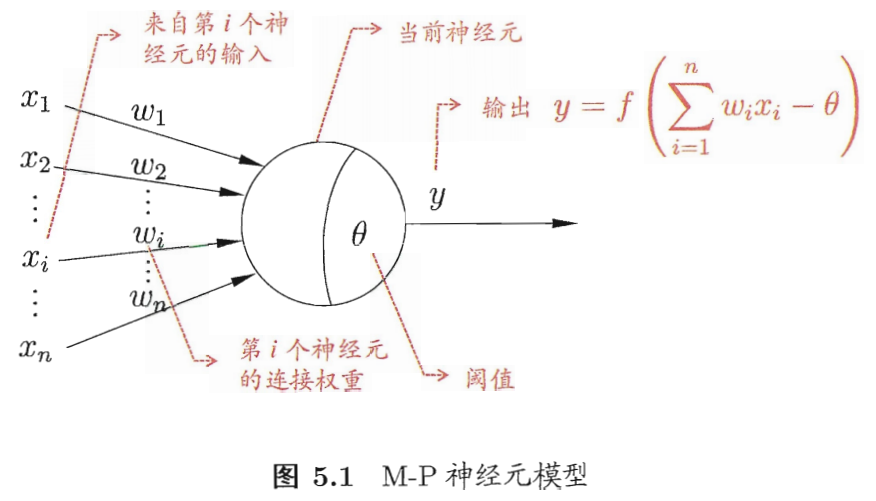
图中f函数为激活函数,
θ
\theta
θ为阈值,
w
T
x
w^Tx
wTx的值超过阈值,激活函数被激活,通过激活函数处理产生神经元的输出。
2、 常见的激活函数
Sigmoid函数、tanh函数、ReLu函数
激活函数常有的性质:
- 非线性
- 可微性
- 单调性
- f ( x ) ≈ x f(x)\approx x f(x)≈x
- 输出值范围
- 计算简单
- 归一化 :要把你需要处理的数据经过处理后(通过某种算法)限制在你需要的一定范围内
sigmoid函数
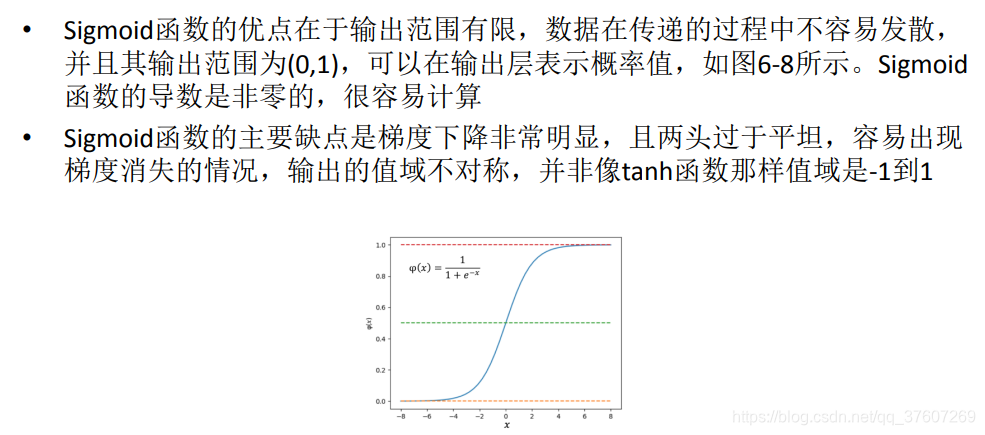
双曲正切函数(tanh函数)
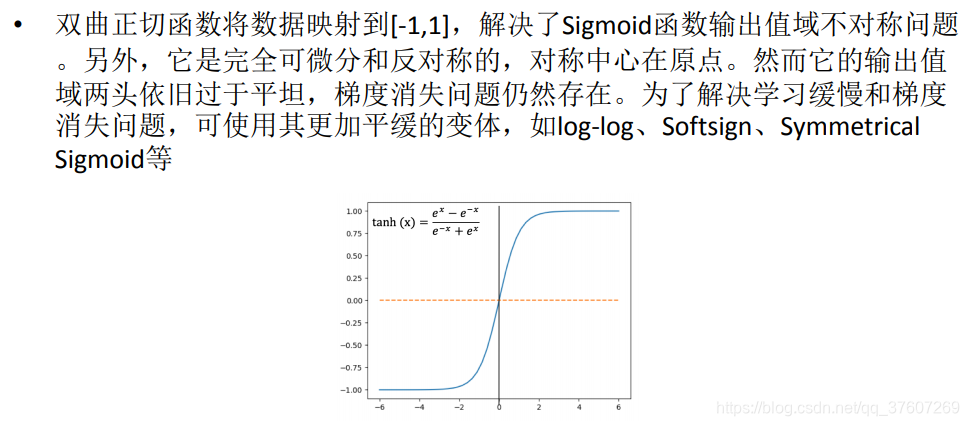
ReLU函数
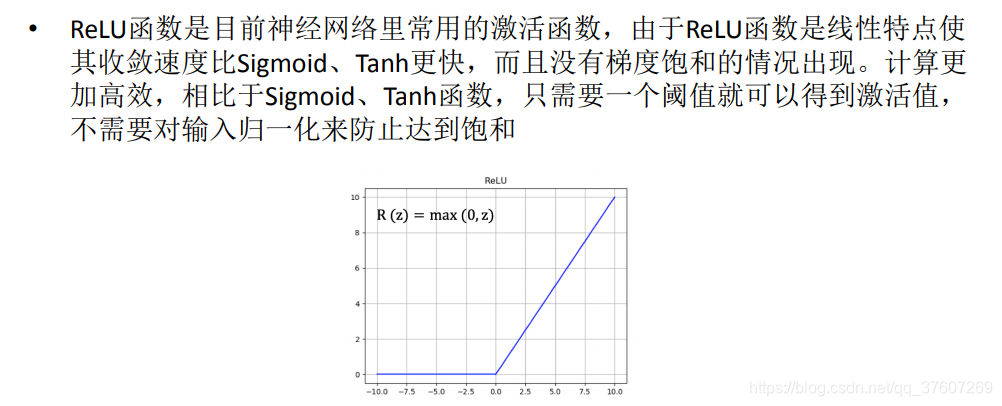
3、训练
没有隐藏层的神经网络,称为感知机。感知机的训练过程见下:
给定训练数据集,权重
w
i
(
i
=
1
,
2
,
3
,
.
.
.
n
)
w_i(i=1,2,3,...n)
wi(i=1,2,3,...n)、阈值
θ
\theta
θ可以通过学习得到。通常情况下阈值作为一个固定的输入 归并到权重中,所以对应的连接权重为
w
n
+
1
w_{n+1}
wn+1。则,问题转化为通过训练数据集得到权重的过程。对于训练样例
(
x
,
y
)
(x,y)
(x,y),假定模型的输出值为
y
^
\hat{y}
y^,那么在学习的过程中权重则这样调整:
w
i
=
w
i
+
△
w
i
w_i=w_i+\triangle w_i
wi=wi+△wi
△
w
i
=
η
(
y
−
y
^
)
x
i
\triangle w_i=\eta(y-\hat y)x_i
△wi=η(y−y^)xi
η
\eta
η称为学习率,取值范围为(0,1)。
对于包含隐藏层的神经网络,通常使用BP算法(误差逆传播算法)进行训练:
BP算法基于梯度下降的策略,以目标的负梯度方向对参数进行调整。BP算法的目标是:最下化训练集D的累计误差:
E
=
1
m
∑
k
=
1
m
E
k
E=\frac{1}{m}\sum\limits_{k=1}^{m}E_k
E=m1k=1∑mEk
假定隐藏层和输出层的激活函数为sigmoid函数。各项参数设定如下:
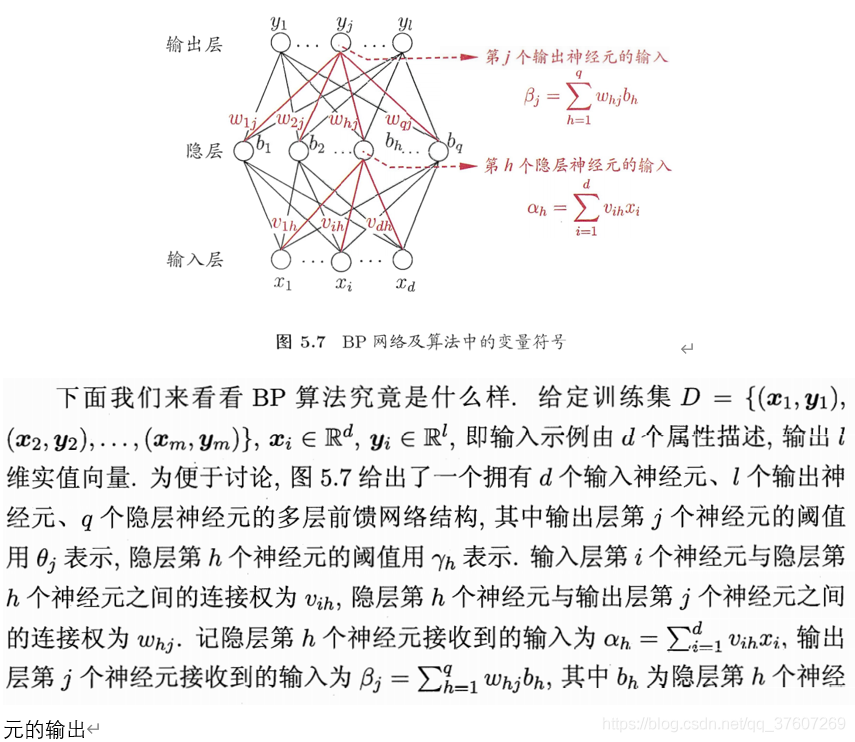

其中
g
i
g_i
gi为:输出层神经元的梯度项。同理,由链式法则可以推出:
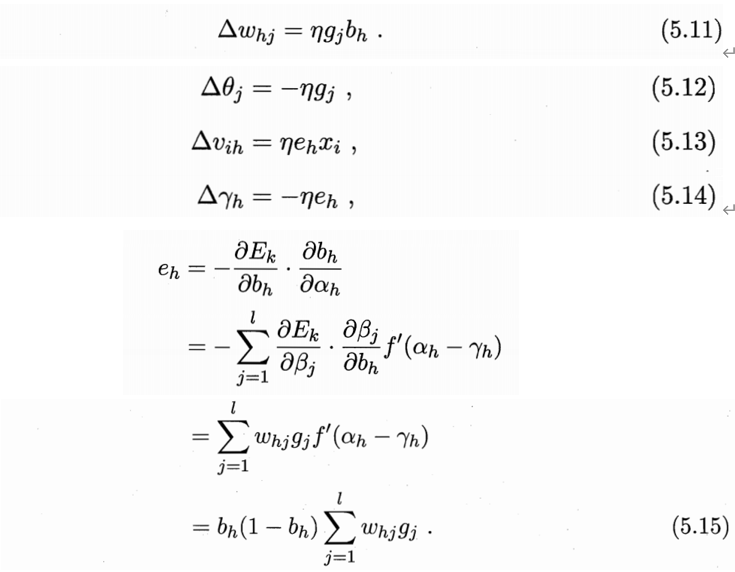
上式
e
h
e_h
eh称为隐层神经元的梯度项,每个参数的更新公式为:
v
=
v
+
△
v
v=v+\triangle v
v=v+△v
BP算法的执行过程见下:

4、总结
BP神经网络易导致过拟合,可使用两种策略:**
1、早停: 将数据分为训练集和验证集,训练集用来训练参数(计算梯度、更新连接权、阈值),验证集用来估计误差。训练集误差降低,验证集误差升高停止训练。
2、正则化: 在误差目标函数中增加一个用于描述网络复杂度的部分,来防止过拟合。例如:
E
=
λ
1
m
∑
k
=
1
m
E
k
+
(
1
−
λ
)
∑
i
w
i
2
E=\lambda\frac{1}{m}\sum\limits_{k=1}^{m}E_k+(1-\lambda)\sum\limits_{i}{w_i}^2
E=λm1k=1∑mEk+(1−λ)i∑wi2,此时训练偏好较小连接权和阈值,使网络更加光滑,从而对过拟合有所缓解。其中
λ
∈
(
0
,
1
)
\lambda\in(0,1)
λ∈(0,1)用于经验误差与网络复杂度的折中,常通过交叉验证法来估计。
关于局部最优和全局最优的解决办法:
1、使用多组不同的初始参数初始化网络,先当与从多个不同点进行搜索。从结果中,找出更接近全局最小的结果。
2、使用随机梯度下降。
来源:周志华《机器学习》